回收余热的空气源热泵热水器的性能模拟及试验研究

2021-12-07王永强

北京工业大学学报 2021年12期

彭斌, 王永强

(兰州理工大学机电工程学院，兰州 730050)

随着能源供应的紧张以及人们环保意识的不断提高，热泵技术因其节能效果明显受到了人们的青睐. 目前，空气源热泵热水器已广泛进入了人们的生活中，但是因空气源热泵热水器的运行对环境温度和湿度的依赖较大[1-3]，仍有很多问题需要解决.

Zhao等[4]对空气源热泵的性能系数(coefficient of performance,COP)与水箱水温进行了试验研究，结果表明，环境温度基本稳定时，随着冷水进水温度的提高，系统的COP降低. 袁朝阳等[5-6]搭建了空气源热泵热水器的试验台，研究了环境温度、初始水温对热泵热水器性能的影响，结果发现，随着环境温度的降低，系统COP逐渐下降，制热能力变差；同一初始水温时，随着加热进行，系统COP下降，不同初始水温时，COP 随初始水温的升高呈现先减小后增大的变化. Fardoun等[7]根据热力学相关知识提出了空气源热泵热水器的准稳态仿真模型，利用Matlab软件模拟了系统的性能参数，空气源热泵相比传统的电热水器在能耗和花费上减少70%，对环境无污染. Amirirad等[8]通过试验和仿真模拟研究了空气源热泵热水器系统在室内条件的性能，结果表明系统的COP随室内温度、湿度的变化在1.5～5.0波动，且相比电容热水器减少年用电量达55%. Ibrahim等[9]研究了空气源热泵热水的动态特性，给出了不同地区环境温度与空气源热泵性能的关系，结果表明平均COP在2.9～5.0；又提出适合热泵运行的控制模式，相比恒温控制可以减少41%的能耗. 刘荣等[10]对热水器机组进行了试验研究，结果显示随水温的升高，机组COP逐渐减小，而压缩机功耗增加，在低温工况下,系统的压比和排气温度增加. Wang等[11]对空气源热泵系统进行了模拟和试验研究，结果表明，该系统的COP在2.0～4.0，具有较高的建筑物季节节能效果.

空气源热泵热水器在低温时，会出现结霜、制热能力下降等问题，将余热作为空气源热泵热水器的低温热源，也为空气源热泵热水器在低温余热的回收利用提供了一定的理论指导. 本文以平均温度40 ℃余热作为空气源热泵热水器的低温热源，建立空气源热泵系统的数学模型，模拟不同空气流量及温度、冷水温度的工况下空气源热泵热水器的运行性能参数，通过对各参数的分析来了解回收余热空气源热泵热水器的动态运行特性，并搭建试验平台验证模拟结果.

1 余热空气源热泵热水器的原理

空气源热泵技术是一种节能、环保的技术. 空气源热泵热水器工作时，蒸发器从空气中吸收大量低温热源，蒸发后的传热工质蒸气经压缩机后变为高温高压的气体，然后通过冷凝器换热，经逆流换热后从冷凝器上端流出进入保温水箱，冷凝后的传热工质通过膨胀阀回到蒸发器中，再被蒸发，如此循环下去. 余热(40 ℃热风)空气源热泵热水器的原理(见图1)是以回收的低温余热作为低温热源，在设备室里供给空气源热泵运行，其原理和空气源热泵热水器的相同，可避免热泵热水器的结霜和制热量下降等问题. 因此余热空气源热泵不受地域和气候的限制，有积极的推广意义.

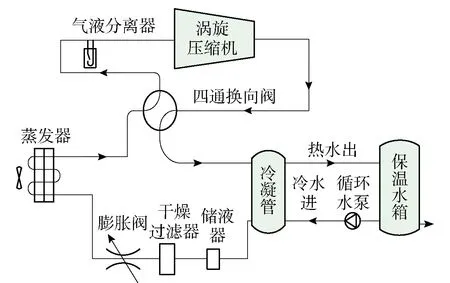
图1 余热空气源热泵热水器系统Fig.1 Heat pump water heater system with waste heat air energy

2 空气源热泵系统的数学模型

2.1 压缩机模型

在对压缩机建模时，考虑建模的精度、计算复杂性、耗时等因素，选用输气系数法.

2.1.1 涡旋压缩机制冷剂质量流量的计算

(1)

式中：Vth为压缩机理论容积输气量,m3/s；vsu为压缩机的吸气口制冷剂的比容，m3/kg；λ为压缩机的输气系数，由λ=λvλpλTλd计算.

2.1.2 容积系数λv和温度系数λT的计算

(2)

(3)

式中：pc、pe分别为冷凝压力和蒸发压力，Pa；Tc、Te分别为冷凝温度和蒸发温度，K；k为压缩机多变指数；c为相对余隙容积，一般在0.01～0.02.

在涡旋压缩机中，由于吸气压力损失很小，泄漏量较小，取压力系数λp和泄漏回收系数λd分别为1和0.95.

2.1.3 涡旋压缩机理论输入功率的计算

(4)

实际输入功率Pre：

(5)

(6)

式中：ηele为压缩机的电效率；ηi为指示效率；ηmo为电动机效率；ηm为机械效率.取ηmo=0.85，ηm=0.8.

2.2 套管冷凝器模型

冷凝器采用稳态分布参数模型，为了满足实际精度的要求，又可以简化计算,在建立冷凝器稳态分布参数模型时提出以下假设[12]：

1) 制冷剂在冷凝器中一维均相流动，不计管内压力损失.

2) 小套管内水的流动为一维均相流动.

3) 管壁热阻和沿轴向的导热均忽略不计.

4) 冷凝器为逆流型换热器.

根据以上的假设，冷凝器的简化模型如图2所示.

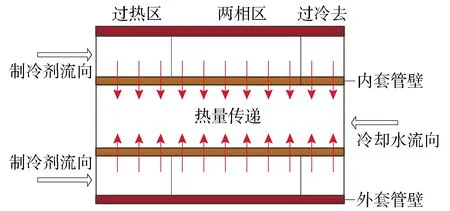
图2 冷凝器模型示意图Fig.2 Condenser model

2.2.1 制冷剂侧的换热量

(7)

式中：Qr-c为制冷剂在冷凝器中放出的热量，kJ；mr-c为制冷剂的质量流量，kg/s；h为制冷剂的焓值，kJ/kg；下标out、in分别表示出口和进口；上标r表示制冷剂侧.

2.2.2 制冷剂侧的换热系数

制冷剂与冷水在冷凝器单相区发生换热是对流换热，求解用迪特斯- 波尔特(Dittus-Boelter)的换热式:

(8)

(9)

式中：Nu为传质努塞尔数；Re为雷诺数；Pr为普朗特数；αr-c为制冷剂侧表面换热系数，W/(m2·K)；μ为制冷剂的动力黏度，m2/s；λzd为制冷剂的导热率，W/(m2·K)；ur为制冷剂的流速，m/s；do-c为冷凝器内套管的外径，m.

制冷剂在冷凝器两相区的换热系数αtr-c采用Shah[13]的换热式：

(10)

(11)

式中：x为两相区的干度；下标l表示液相；αl为假设所有制冷剂全部以液相流动时的换热系数，W/(m2·K)；ptr为制冷剂在两相区的实际压力，Pa；pcr为制冷剂的临界压力，Pa；di-c为冷凝器内套管的内径，m.

2.2.3 水侧的换热量

(12)

式中：Qw-c为水在冷凝器中吸收的热量，kJ；mw-c为水的质量流量，kg/s；cp-w为水的定压比容，kJ/(kg·K)；T为水的温度，℃；上标w表示水侧.

2.2.4 水侧的换热系数

套管冷凝器一般制成螺旋盘管式，冷却水在其内与制冷剂发生对流换热，换热只发生在管内外壁壁面，因此水侧换热系数计算式[14]为：

(13)

(14)

制冷剂和冷却水在套管内换热损失的热量用漏热系数φc(一般取0.9 )来衡量，即φcQr-c=Qw-c.

2.2.5 微元的换热方程及长度

(15)

(16)

式中：Ar-c为制冷剂侧换热面积，m2；ΔTm为套管冷凝器微元的平均温差，K.

忽略制冷剂侧的热阻，总的换热系数Uc以内套管的外表面为基准求解：

(17)

式中：αr为冷剂侧传热系数，W/(m2·K)；λzt为冷凝器紫铜套管导热系数，W/(m2·K).

2.3 电子膨胀阀模型

目前最常用的电子膨胀阀模型是采用水力学流量公式描述电子膨胀阀的流量特性[15]：

(18)

(19)

式中：mth为制冷剂流量，kg/s；CD为流量系数；A为阀的流通面积，m2；ρ为进口制冷剂的密度，kg/m3；ν为制冷剂出口比容，m3/kg.

电动式电子膨胀阀是步进电机驱动的电子膨胀阀,驱动电路输入脉冲给步进电机,带动阀针上下移动,进而改变膨胀阀的开度.如图3所示.

图3 电子膨胀阀示意图Fig.3 Schematic diagram of electronic expansion valve

阀针的位移量dX计算式为

(20)

式中：N为电子膨胀阀从全开到全关步进电机的脉冲数；K为步进电机的输入脉冲数；dX0为阀针从电子膨胀阀全开到全关的位移量，m.

电子膨胀阀的开度

(21)

则电子膨胀阀的流通面积为

(22)

式中：d为阀孔直径，m；Ad为阀孔截面积，m2.

2.4 蒸发器模型

蒸发器也使用分布参数法模型，建模方法类似于冷凝器的.在对蒸发器建立模型时，为了简化和计算的需要，做出以下假设[12]:

1) 制冷剂和空气处于一维流动.

2) 蒸发器管壁的径向温度不发生变化，不考虑热阻的影响.

3) 制冷剂在蒸发器管中的压力沿管长不发生变化.

图4是蒸发器的物理模型示意图.

图4 蒸发器模型示意图Fig.4 Schematic diagram of evaporator model

2.4.1 制冷剂侧的换热量

(23)

2.4.2 制冷剂侧的换热系数

在过热区，换热系数αer用Petukhov-Popov的计算式为

(24)

f=(1.82lgRe-1.64)-2

(25)

式中：f为湍流摩擦因子；λ为制冷剂的导热系数，W/(m·K).

在两相区，换热系数αthr用Kandlikar[16]的计算式表示为

(26)

(27)

(28)

(29)

(30)

式中：αl1为液相制冷剂流过表面时的换热系数，W/(m2·K)；Frl为液相制冷剂弗劳德数；B0为沸腾特征数；Ffl为制冷剂性质的量纲一的数；gr为质量流率，kg/(m2·s)；x为制冷剂干度；μl为液相制冷剂的动力黏度，Pa·s；Prl为液相制冷剂的普朗特数；λl为液相制冷剂的导热系数，W/(m·K)；ρg、ρl分别为气相和液相制冷剂的密度，kg/m3；q为热量密度，W/m2；r为汽化潜热，kJ/kg；C0～C5为常数，大小由C0决定.

2.4.3 空气侧的换热量

(31)

(32)

2.4.4 空气侧的换热系数

在空气侧，换热系数αae根据李妩等[17]在试验基础上得出的关联式

(33)

(34)

(35)

式中：λa为空气的热导率，W/(m·K)；Re为空气的雷诺数；s为翅片间距；s2为沿空气流方向的管间距，m；sl为垂直于流方向的管间距，m；db为翅根直径，m；Ng为管排数；δf为翅片厚度.

2.4.5 微元的换热方程及长度

(36)

QΔe=UeAr-in(Trm-Ttm)

(37)

(38)

式中：Ue为基于制冷剂侧换热面积的总换热系数，W/(m2·K).

在实际蒸发器的工作过程中，空气侧的换热量和制冷剂所吸收的热量是不相等的，通过蒸发器的漏热系数φe使两者相等.

2.5 空气源热泵系统求解流程

在求解系统模型时，先假设系统的冷凝压力、蒸发压力及蒸发器出口温度，由此先计算出压缩机的质量流量以及其出口参数作为入口参数对冷凝器进行求解，将计算出的冷凝器出口参数作为电子膨胀阀的入口参数，再计算电子膨胀阀的质量流量，并与压缩机的质量流量相比较，对冷凝压力进行修正. 满足精度要求后进行蒸发器的数值计算，将蒸发器的出口温度计算结果与假设值进行比较，求解流程如图5所示.

图5 空气源热泵系统求解流程Fig.5 Solution flow chart of air energy heat pump system

3 试验研究

为了进一步分析系统在不同工况下性能参数的变化和验证系统数学模型的准确性，搭建了余热空气源热泵热水器的试验测试平台. 测量在变余热温度和风量及水温条件下系统的排气温度、压比、功率、制热量以及性能系数COP的变化. 图6所示为测试样机的实物图，并依据图7的测试系统原理图搭建了空气源热泵热水器的测试平台，并将模拟与测试数据进行了对比.

图6 测试样机的实物Fig.6 Physical figure of test prototype

P—压力测试点 T—温度测试点 G—水流量测试点黑色实线框内为热泵系统红色虚线框内为水循环系统图7 空气源热泵热水器系统测试原理Fig.7 Test principle of air energy heat pump water heater system

4 模拟结果对比分析

4.1 热风温度对试验的影响

图8是热泵系统参数随热风温度的变化，在热风温度逐渐增加时，系统的制热量增加，在35 ℃之前，制热量的误差基本为0；35 ℃之后，由于试验误差导致试验值模拟值大于试验值，制热量的误差逐渐变大. 压缩机功耗的误差在38 ℃之后基本保持不变，但在38 ℃之前误差较大，原因主要是随着热风温度的增加，压缩机功耗的试验值进一步增加. 温度升高时，蒸发温度升高，导致系统的制冷剂质量流量增大，压缩机的功耗增加，这也使得在38 ℃附近时系统的COP的偏差最小，在30 ℃时的偏差最大，系统的压比和排气温度的误差基本保持稳定. 综合考虑系统的制热量和压缩机功耗以及COP，得出的结论是热风温度在45 ℃左右时系统的各性能较佳，在热风温度高于50 ℃时，压缩机功耗增加较大导致系统COP增加缓慢. 试验偏差在10%以内，建立的模型具有一定的准确性.

图8 热风温度对试验的影响Fig.8 Effect of hot air temperature on test

4.2 热风风量对试验的影响

如图9是热泵系统参数随热风风量的变化，在热风风量逐渐增加时，系统的制热量先增加后趋于稳定，压缩机的功耗在增加，这是因为风速较小时，在过热区还来不及蒸发的液态制冷剂进入两相区，由于两相区所占比例更大，在风速增大的过程中液态制冷剂在两相区域内得到完全蒸发换热；因此在风量刚开始增大时蒸发器侧的换热良好. 在风速持续变大的过程中，过热区长度增大，同时两相区长度减小，这促使在过热区中大部分液态制冷剂被蒸发，虽然蒸发器侧的传热系数增大，但是换热量却基本维持不变了. 因此，系统的制热COP呈现先增加后减小的趋势，存在一个最大值. 增大热风风量时压缩机的功耗增大，不利于系统的稳定运行，但系统的制热量先增加较快，后基本保持不变，综合考虑系统的制热量和压缩机功耗以及COP，得出热风风量控制在5 000 m3/h以内时系统的各项参数较佳，而不是越大越好，较大的风速也会使风机发出的噪声更大. 系统的排气温度和热风风量呈正相关，偏差基本保持在10%以内.

图9 热风风量对试验的影响Fig.9 Effect of hot air volume on test

4.3 冷水温度对试验的影响

图10是热泵系统参数随冷水温度的变化，在进入冷凝器端的冷水温度逐渐增加时，系统的制热量减少，压缩机的功耗增加，而系统的COP呈减小的趋势，这是由制热量和功耗的比值决定的. 增大冷水温度时，系统COP的变化幅度相对于增加热风温度时的小些. 随冷水温度的增加，系统压比的偏差是逐渐减小的，在冷水温度为10 ℃时，压比的偏差最大值为12.5%，但压比的值小于4，可保证压缩机的正常工作. 系统的排气温度随冷水温度的增加而增加，其模拟值和试验值的变化趋势一致，偏差基本不变.