基于自监督循环卷积神经网络的位姿估计方法

阮晓钢， 李 昂， 黄 静

(1. 北京工业大学信息学部， 北京 100124； 2.计算智能与智能系统北京市重点实验室， 北京 100124)

视觉同时定位与地图构建(simultaneous localization and mapping，SLAM)是实现自动驾驶和虚拟现实等新兴技术的基础，而视觉里程计作为视觉SLAM的前端[1]，能够描述机器人、车辆等移动物体的自我运动过程，从而实现定位功能. 视觉里程计进行定位的基本模式为：首先，利用摄像机捕获连续运动时间内的图像序列；然后，通过算法计算相邻图像间的运动关系；最后，输出相机的相对姿态参数. 这一过程也称为视觉位姿估计[2]. 准确的位姿估计是实现导航任务的关键.

传统的位姿估计方法主要为特征法[3-5]和直接法[6-8]. 特征法充分利用了图像的几何信息，主要包含特征提取、特征匹配、误匹配剔除和运动估计等步骤，目前已经成为一种标准的黄金法则，而直接法则使用了图像的光度信息，通过直接计算像素值估计相机的运动. 上述2类方法虽然在准确性和鲁棒性上展示了不错的性能，但仍然存在一些关键性问题. 特征法提取的是人为设计的低级特征，只适用于具有明显特征的场景，当面对纹理单一、存在动态物体的场景时，难以提取到有效的特征. 直接法虽然不需要进行特征提取，但在利用图像的像素值时使用了光度一致性假设，这种假设在面对光照变化明显的场景时难以成立，将直接导致算法失败.

近年来，深度学习已经在许多计算机视觉任务中取得了很好的效果，其中卷积神经网络通过自主学习方式能够提取图像的高级语义特征，而具有语义的图像信息是很难凭借人类的知识和经验建模获取的. 这种优势使得卷积神经网络在图像分类[9]、目标检测[10]、语义分割[11]方面表现出的性能远远超越了传统人工特征提取的方法，为视觉位姿估计提供了新的解决方案[12]. Kendall等提出了PoseNet[13]模型，该方法基于GoogleNet[14]网络输出六自由度位姿，可用于相机的重定位. 但是GoogleNet等常用卷积神经网络本质上是为了解决图像识别和分类问题，从而提取图像内容特征，而位姿估计需要利用与图像运动相关的特征. Costante等[15]通过结合使用光流图和卷积神经网络来学习2帧图像间的相对位姿，虽然利用光流描述了图像的运动信息，但由于相机在短时间内运动变化很小，所以相机位姿不仅与相邻图像有关，还应该受到多帧的约束，而该方法中的卷积神经网络(convolutional neural networks，CNN)结构无法对图像序列进行学习. 为此，Wang等[16]提出了DeepVO模型，通过利用长短期记忆(long short term memory，LSTM)网络[17]进行时序建模，学习多帧图像间的运动关联. 但是，以上深度学习方法主要采用了监督学习，需要数据集提供真实的相机位姿数据. 然而在实际应用中，获取具有真实位姿数据的数据集十分昂贵，并且现有的监督训练数据集数量仍然有限.

针对上述问题，本文提出一种结合卷积神经网络和循环神经网络的视觉里程计(recurrent convolutional neural networks visual odometry，RCNNVO )模型. RCNNVO模型通过输入图像序列，直接输出相机的相对位姿.

1 相机相对位姿

为了同时描述相机的旋转和平移运动，定义了变换矩阵T，其中包含了旋转矩阵R和平移向量t，公式为

(1)

假设在t和t+1时刻，相机拍摄了2幅相邻图像It和It+1，对应世界坐标系下的绝对位姿分别为Tt和Tt+1，则相机在t和t+1时刻之间通过运动产生的变换矩阵为

(2)

虽然变换矩阵将旋转和平移运动整合到一起，但是变换矩阵有16个元素，而旋转和平移总共只有6个自由度，因此，存在多余的信息.

考虑到信息冗余主要存在于旋转矩阵R中，因此，可采用欧拉角来刻画相机的旋转运动，欧拉角只包含3个分量，每个分量代表物体绕不同坐标轴的旋转角度，正好对应旋转运动的3个自由度.根据物体绕坐标轴旋转的先后顺序，可以有多种欧拉角表示方法，本文采用的欧拉角定义方式如图1所示，图中xyz坐标轴为参考坐标系，XYZ坐标轴为相机旋转之后的坐标系，相机旋转的先后顺序为：1) 绕参考坐标系的z轴旋转，得到偏航角α.2) 绕2个坐标系相交线N旋转，得到俯仰角β.3) 绕参考坐标系的Z轴旋转，得到横滚角γ.最终欧拉角可以表示为向量p=[α,β,γ]T.通过结合欧拉角p和平移向量t可以描述相机的绝对位姿，即

图1 欧拉角示意图Fig.1 Schematic diagram of Euler angles

(3)

相机的相对位姿可以表示为

(4)

2 自监督循环卷积神经网络模型

本文构建的RCNNVO模型的详细结构如图2所示， RCNNVO中结合了卷积神经网络、循环神经网络和全连接层3个部分结构，网络的训练方式为自监督学习.

本文提出的位姿估计方法的完整计算步骤如下:

1) 将图像序列输入到RCNNVO中, 序列长度为k+1.

2) 分别使用CNN网络提取序列中相邻图像间的特征，如{(I1,I2),(I2,I3),…,(Ik,Ik+1)}.

3) 将CNN输出的特征作为时序数据, 利用循环神经网络(recurrent neural networks,RNN)进行时序建模，建立多个位姿之间的关联.

4) 最后使用全连接层进行降维, 得到相邻图像间的相对位姿, 用六自由度向量表示.

2.1 基于CNN的运动特征提取

卷积神经网络主要解决图像分类问题，因此，大多CNN预训练模型是为了提取与图像内容有关的特征，而相机位姿估计与图像分类区别很大.首先是图像分类任务每次只需要提取一幅图像的特征，而位姿估计计算的是相邻图像的相对位姿，需要同时处理2幅图像；其次位姿估计是一种回归问题，图像外观特征并不适用于估计位姿.如图3所示，图中对比了2种不同的相机运动情况，每种情况包含4幅图像，其中每一行的图像对代表一个相机的相对运动.从图3(a)中可以看出，上下2组图像对描述的场景十分相似，如果使用专门用于图像分类的CNN模型对2组图像进行特征提取，将会得到相同的特征，最终输出的2个位姿结果很接近.然而2组图像对对应的相机相对运动却是不同的，第1组主要为旋转运动，第2组主要为平移运动.从图3(b)中可以看出，上下2组图像对描述的是不同场景，因此，提取到的图像特征完全不同，那么对应输出的位姿结果则差别很大，而实际上2组图像对描述的是相同的平移运动.因此，为了能够输出准确的相机位姿，应该采用一种能够提取出图像运动特征的CNN模型.

图3 2种不同的相机运动情况Fig.3 Two different camera motions

由于光流概念的引入使得相邻图像间的运动关系可以用光流信息表示，本文参照了卷积神经网络模型Flownet[18]，通过修改FlowNet的子网络FlowNetSimple构建了RCNNVO中的CNN部分，用于提取图像运动特征.CNN的各层参数如表1所示.该CNN模型共包含10个卷积层，其中第1个卷积层的卷积核大小为7×7，第2层、第3层的卷积核大小减小为5×5，后面7层的卷积核大小再次缩小到3×3，卷积核的尺寸越小，网络越能捕捉到更细微的特征.随着网络层数的加深，不断增加卷积核数量，使得每层可以输出更多的特征图，提取更多的局部特征.

表1 卷积神经网络模型的各层参数Table 1 Parameters of each layer of CNN

CNN使用图像序列作为输入，序列长度大于2，序列中每幅图像的尺寸均为1 280×384像素.在逐层学习图像运动特征的过程中，在每个卷积层之后添加批量归一化[19]操作，使得卷积变换前后数据分布保持不变，并加快网络训练速度，防止在反向传播中发生梯度爆炸.为了避免产生过拟合现象，在每个批量归一化操作后使用修正线性单元(rectified linear unit，ReLU)使输出非线性化，增强CNN的泛化性能.在完成相邻图像间的运动特征学习后，将CNN最后一个卷积层输出的特征图输入到后面的RNN结构.

2.2 基于循环神经网络的时序建模

虽然CNN结构通过提取运动特征建立了相邻图像间的运动关系，但事实上由于相机的拍摄频率较快，短时间内的相机运动应该是相似的；因此，当前时刻相机的位姿不仅与相邻图像有关，还应该受到一定范围内多幅图像的位姿影响.为了输出更准确的位姿结果，网络模型需要考虑多帧之间的运动关联.然而CNN由于自身的结构限制，不能同时输入多个数据，并且无法利用上一时刻的结果对下一时刻的输出进行预测.

循环神经网络(recurrent neural networks，RNN)十分适合处理这种时序数据问题，可以在计算下一时刻相邻图像间的运动关系时提供之前时刻保留的位姿信息.从理论上讲，简单的RNN可以学习任意长度的序列，但反向传播过程中存在梯度消失问题，导致其在实际应用中受到限制.为了解决简单的RNN结构难以处理的长期依赖问题, 诞生了LSTM网络.虽然LSTM擅长处理长序列，但其本质上是为了解决语音识别、数据预测等问题，主要接收一维输入信号，并不适合处理图像.原因是在其内部结构中，输入与权重的计算方式类似于全连接，当输入数据为二维图像时，由于图像中像素点与周围的像素点存在很强的相关性，在使用全连接方式进行计算时会破坏图像的局部空间结构，从而无法准确地描述图像特征.因此，RCNNVO中使用了卷积长短期记忆(convolutional LSTM，ConvLSTM)网络[20]，其内部结构如图4所示.ConvLSTM在LSTM的基础上将输入与门的连接方式改成了局部连接，对输入与权值进行卷积操作.ConvLSTM不仅能够完成时序建模，还可以通过卷积操作进一步学习图像间的运动特征.

图4 ConvLSTM的内部结构Fig.4 Internal structure of ConvLSTM

ConvLSTM的内部结构依然使用了3个门单元，假设当前时刻为t，输入为xt，上一时刻的隐藏状态为ht-1，则ConvLSTM的输出及状态更新的计算方式为

(5)

式中：σ为sigmoid激活函数；*表示卷积运算；⊙表示2个矩阵或向量对应元素相乘；W为卷积核权重；b为偏置；it、ft、Ct、ot、ht均为三维张量，第1个维度为时间，后2个维度为图像的长和宽.

RCNNVO中RNN结构由2个ConvLSTM叠加构成，每个ConvLSTM层包含1 000个隐藏单元，卷积核大小设置为3×3.其中第1个ConvLSTM层连接在CNN的卷积层Conv_10之后，第2个ConvLSTM层连接在第1个ConvLSTM层之后.为了保持原始的数据分布，2个ConvLSTM层中均使用了激活函数ReLU.

为了计算相机位姿，RCNNVO在第2个ConvLSTM层之后连接了2个全连接层，神经元个数分别为100和6，其中最后一个全连接层的输出为RCNNVO网络估计出的相机相对位姿，用欧拉角和平移向量共同表示.

2.3 基于自监督的损失函数设计

对于目前现有的监督学习方法，如DeepVO[16]，其设计的损失函数为所有图像位姿估计值与真实值之间的平移误差和旋转误差之和.这种训练方法需要获取每个图像的真实位姿，使得算法的使用场景受到限制.

为了在训练网络的过程中不受数据集的影响，本文遵循了间接法SLAM的思想[21].间接法SLAM在位姿估计中表现出的良好性能，主要源于其可以从原始图像中提取到稳定的局部特征，如关键点、线段等，因为这些特征的描述符具有很强的尺度不变性，所以通过特征匹配能够建立相邻图像间的几何关系，而这种几何关系仿照了人类对三维空间的感知.因此，本文考虑离线生成这种几何成分并集成到RCNNVO框架中，使算法在不需要真实位姿数据的情况下自主生成位姿约束，从而优化网络参数.

间接法实现位姿估计有2个基本步骤：一个是特征匹配，另一个是几何验证[21].假设有一对相邻图像(I1,I2)，通过特征提取与匹配算法获得了一组匹配点的坐标集合{(Pi,Qi)}，则根据匹配点的空间位置关系可以建立几何关系

(6)

由于RCNNVO在输出相机位姿时使用欧拉角描述了旋转运动，而式(6)在计算基本矩阵时使用的是旋转矩阵，所以需要进行欧拉角与旋转矩阵的变换.假设输出的欧拉角为r12=[α,β,γ]T，则对应的旋转矩阵为

(7)

通过特征匹配建立的对极几何如图5所示.图中：I1和I2为像平面；O1和O2为2个相机的光圈中心；M代表空间点.O1、O2、M三点相连形成的蓝色三角形称为极平面.E1、E2为连线O1O2与2个像平面的交点，P和Q分别为点M在像平面I1、I2上的真实投影，Q′为P根据本文算法的初始位姿估计值计算出的匹配点.红色虚线l为极平面与像平面I2形成的相交线，称为极线.

(8)

图5 基于特征匹配和对极几何的对极约束Fig.5 Geometric constraint enforced by pairwise matching and epipolar geometry

(9)

3 实验结果

本文通过使用公开数据集验证了自监督循环卷积神经网络模型RCNNVO的性能，评估位姿结果的指标为旋转误差和平移误差.实验所使用的深度学习框架为PyTorch-1.0.1，系统为Ubuntu16.04，计算机配置为：32 GB内存、GTX1080显卡、Intel Xeon E5-2603 V3处理器.

3.1 实验数据集

实验选择KITTI Odometry数据集[22]对RCNNVO模型的性能进行评估.KITTI Odometry数据集广泛应用于各种视觉SLAM和视觉里程计算法，其包含22个不同场景的图像序列，图像的获取方式主要为：在汽车顶部安装双目相机，然后在城市、郊区、乡村等地点行驶的过程中进行拍摄，相机的拍摄频率为10 Hz.22个序列中只有前11个序列提供了相机内部参数和每个图像对应的真实姿态数据，这些真实数据是通过全球定位系统、惯性测量单元等多种高精度传感器计算而来.其中序列00-03的图像尺寸为1 241×376像素，序列04-10的图像尺寸为1 226×370像素，为了符合网络对输入数据的要求，将所有图像的尺寸调整为1 280×384像素.

考虑到训练集和验证集的图像种类划分，本文使用序列00、01、02、06、08对RCNNVO模型进行训练，并选择一定数量的数据进行验证，然后使用序列03、04、05、07、09、10对RCNNVO模型进行测试.训练集和验证集使用的图像均由双目相机中的左相机所采集.

3.2 训练过程

本文提出了自监督的训练方式，其损失函数的计算需要相邻图像间的匹配点坐标.因此，首先使用基于图形处理器的尺度不变特征变换(scale invariant feature transform,SIFT)算法[23]对每幅图像提取大约1 000个SIFT特征[24]，并通过特征匹配获得相邻图像间匹配点的坐标.然后利用RANSAC算法对匹配结果进行筛选，去除不正确的结果.考虑到算法的实时性和计算机配置等问题，从每对相邻图像中随机抽取100个匹配点用于损失函数的计算.

在训练过程中，使用Adam优化器更新网络参数，其中β1=0.900，β2=0.999，初始学习率设置为0.000 1，batch size设为8.随着训练次数的增大，适当降低学习率.在训练开始前使用xavier方法对网络参数中的权重进行初始化，对偏置进行零初始化.为了加快模型的训练速度，防止产生过拟合现象，在所有ConvLSTM层和全连接层中添加dropout机制.

3.3 误差分析

将训练好的RCNNVO模型在序列03、04、05、07、09、10上进行测试，并与其他3种先进的视觉里程计系统进行比较，其中ORB-SLAM(不包含闭合检测模块)[5]、VISO2-Mono[25]为单目系统，而VISO2-Stereo[25]为双目系统，其结果仅作为参考.实验使用的性能评价指标为KITTI官方设定的4种均方根误差RMSE，分别为不同路径长度下的平均平移误差和平均旋转误差、不同相机运动速度下的平均平移误差和平均旋转误差.其中路径长度均为100的倍数，范围为100～800 m.不同路径长度下的误差计算方法为：首先，将完整行驶路径按照设置的路径长度平均分成多个子路径；然后，计算每个子路径下的平移误差和旋转误差；最后，分别求取所有子路径的旋转误差和平移误差的平均值.相机运动速度等同于拍摄图像时汽车的行驶速度，由于每个序列的平均速度都不相同，所以首先找出测试集所有序列中的最低速度和最高速度，然后再在二者之间平均选取6个速度值.

4种方法在不同评价指标下的误差如图6所示.可以看出，在大多数情况下，RCNNVO的误差比ORB-SLAM和VISO2-M的误差小，说明CNN和ConvLSTM相结合的网络结构可以学习到图像中与运动相关的特征.但随着相机运动速度的增加，RCNNVO的误差有增大的趋势，出现这种问题的原因主要是训练集中缺少运动速度较快的样本，只有少数图像序列的速度在50 km/h以上，因此，网络在预测高速运动下的平移和旋转信息时较为困难.

图6 不同算法在4种指标下的误差Fig.6 Errors of different algorithms based on four indexes

3.4 运动轨迹可视化及精度评估

为了直观地展示算法的性能，分别将RCNNVO、ORB-SLAM、VISO2-M、VISO2-S在序列03、04、05、07、09、10上估计的运动轨迹进行了可视化处理，如图7所示.图中以真实位姿数据生成的运动轨迹作为标准，用黑色虚线表示.可以看出，4种算法大致上都恢复出了真实运动轨迹的形状，而RCNNVO模型估计的运动轨迹要优于ORB-SLAM和VISO2-M，更接近于真实轨迹，但略逊于VISO2-S.一方面是因为VISO2-S是双目算法，在估计相机位姿时可以通过左目相机和右目相机拍摄的2幅图像获取尺度信息，因此，计算结果更加准确；另一方面是因为RCNNVO的训练样本不够多，如果能够用更充足的数据集训练网络，可能会进一步提升网络输出的位姿精度.不同算法在测试集上的具体表现如表2所示，表中各序列的位姿精度评价指标为所有路径长度(100 m, 200 m, …, 800 m)的平均平移误差和平均旋转误差.其中平移误差以“%”来度量，旋转误差以“(°)”来度量.在4种对比方法中，DeepVO为基于监督学习的位姿估计算法，其网络结构由CNN和LSTM构成，因为DeepVO的作者没有开放源代码，所以表中直接使用了文献[16]中的实验数据.实验结果表明，本文算法优于DeepVO、ORB-SLAM、VISO2-M三种单目算法，证明了自监督训练方法的可行性.

图7 不同算法在序列03、04、05、07、09、10上生成的运动轨迹Fig.7 Motion trajectories generated by different algorithms on sequence 03，04，05，07，09 and 10

表2 不同方法在测试集上的平均平移误差和旋转误差Table 2 Average translation and rotation errors of different methods on testing datasets

另外，本文还在序列11、12上对RCNNVO模型行了测试，序列11、12没有提供真实位姿数据，并且车辆的行驶速度也快于前面11个序列，因此，在相机拍摄频率保持不变的情况，相邻图像间的相机运动则更加剧烈，这将十分考验算法的泛化能力.图8展示了不同算法估计的运动轨迹的可视化结果，由于数据集缺少真实数据，所以使用了VISO2-M、VISO2-S的实验结果与本文算法进行对比，并以VISO2-S的结果作为参考.可以看出，相较于VISO2-M方法，RCNNVO的运动轨迹更接近于VISO2-S，这意味着本方法在没有真实位姿数据的情况下仍然可以工作，并展现出了不错的泛化能力.

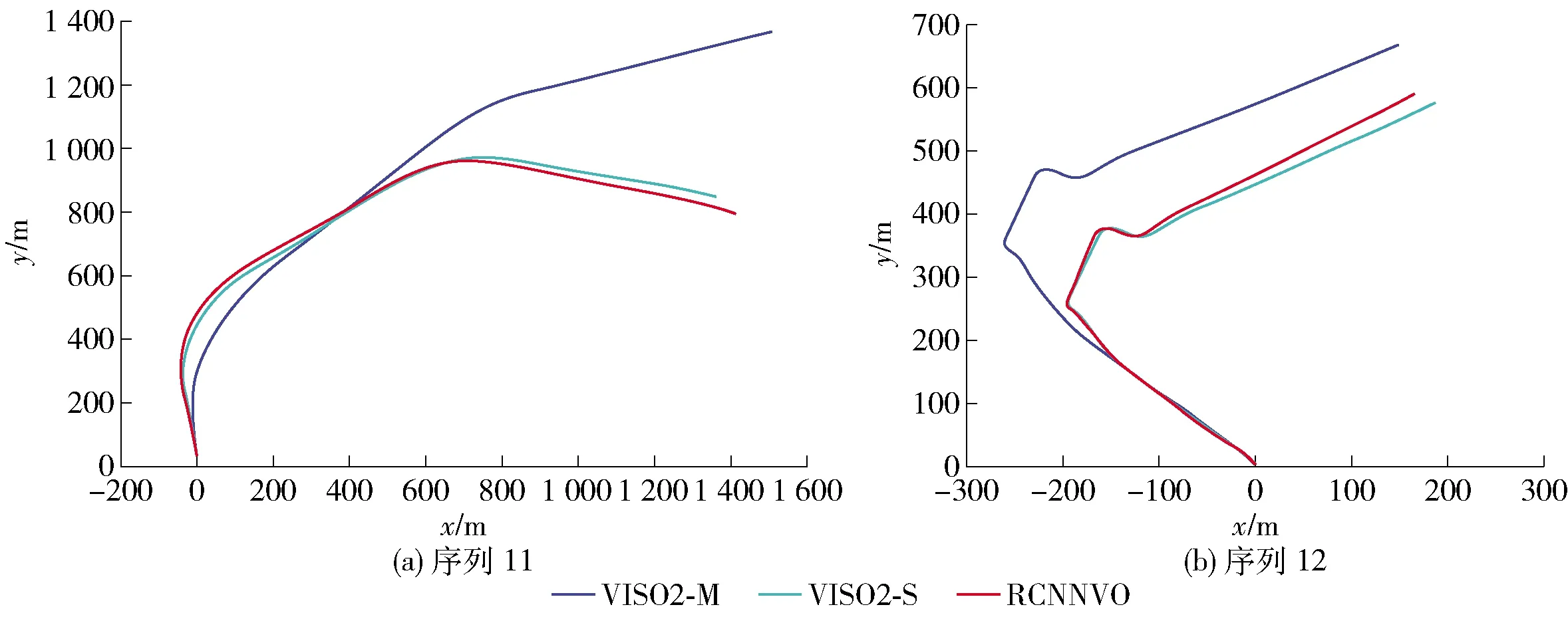
图8 不同算法在序列11、12上生成的运动轨迹Fig.8 Motion trajectories generated by different algorithms on sequence 11 and 12

4 结论

1) 本文提出了一种基于自监督循环卷积神经网络的位姿估计模型RCNNVO.该模型以图像序列为输入，首先，使用CNN结构提取相邻图像之间的运动特征；然后，利用ConvLSTM的卷积操作进一步学习图像的空间特征，通过时序建模融合多幅图像信息，并建立连续多帧之间的运动约束；最后，输出相邻图像间的六自由度相对位姿.

2) 监督学习需要数据集提供真实的位姿信息，而实际数据普遍缺乏位姿信息标注,导致可供训练的样本集有限.因此，本文提出了一种自监督的网络训练方法，通过特征匹配和对极几何建立基于对极约束的损失函数，以自主生成标签的方式优化网络参数.

3) 本文在KITTI Odometry数据集上对算法的性能进行评估，实验结果证明，RCNNVO模型的位姿精度优于先进的单目系统ORB-SLAM和VISO2-M，并且其预训练模型可以泛化到其他未知场景.