TGO及初始裂纹对热障涂层裂纹形核与扩展影响的有限元分析
2021-12-04李佐君钟舜聪戴晨煜
李佐君, 梁 伟, 钟舜聪, 戴晨煜
(福州大学 机械工程及自动化学院 光学太赫兹及无损检测实验室,福州 350108)
0 引言
燃气轮机是现代航空工业的重要支柱,是国家重大装备制造水平的标志。热障涂层(Thermal barrier coatings,TBCs)技术是发展先进重型燃气轮机的核心技术之一,它在轮机基体表面覆盖一层具有低热导率、高稳定性的隔热材料,不仅具有热障效果,而且还能防止氧化、腐蚀以及外来物冲蚀等对叶片造成的损伤[1]。目前,F级重型燃气轮机的燃气温度已达到1400 ℃,未来重型燃气轮机的燃气温度将超过1700 ℃。极端高温的工作环境加剧了热障涂层的失效破坏,极大缩短了燃气轮机的安全服役寿命,所以研究热障涂层的失效机理对提高燃气轮机的安全性具有重要意义[2]。
经典的TBCs系统是在镍基超合金基底(SUB)上覆盖一层顶部陶瓷层(TC),在中间有一层金属粘结层,粘结层不仅使得陶瓷层能牢固附着在基底上,而且能够降低由于TC和基底的热膨胀系数失配产生的失配应力[2-3]。通常TC的主要材料为氧化钇部分稳定氧化锆(YSZ),粘结层为MCrAlY(M代表Ni或Co或Co+Ni)[4]。初期,在高温服役条件下,由于元素扩散,在陶瓷层与粘结层界面之间,粘结层中的Al与从陶瓷层中扩散进来的O反应生成一层很薄的热生长氧化物(TGO),其主要成分为Al2O3。TGO的形成阻止粘结层氧化的进一步发生,在一定程度上减缓了粘结层氧化速率,但随着服役时间的增加,TGO中致密的Al2O3与Ni、Cr的氧化物发生反应,生成了尖晶石等氧化物[5]。Al2O3的耗尽将极大提高粘结层氧化速率,Al2O3的慢速生长转变为尖晶石的快速增长导致TGO层产生巨大的应力,同时TGO层内部出现大量孔洞和微裂纹。随着微裂纹的不断萌生、扩展,最终导致大量裂纹贯穿,形成涂层大范围屈曲、剥落[6-7]。
由于裂纹萌生与扩展是造成TBCs失效的主要因素,为了深入探索TBCs的失效机理,国内外学者采用各种实验方法与数值模拟方法对TBCs开展了大量研究。Padture等[2]介绍了APS TBCs的4种失效机理;Wu[8]建立了热障涂层的裂纹数密度理论模型并研究了TGO生长对裂纹形成和扩展的影响;Ranjbar-Far[9]等模拟了热循环、氧化层生长和不同界面形貌对涂层裂纹扩展的影响,但未对任意随机裂纹扩展进行模拟;Torkashvand等[10]研究了不同TGO厚度的抗热冲击的性能,认为TGO厚度在2~3 μm时具有积极作用的抵抗热冲击;Dong等[11]研究了由于TGO厚度变化而引起失效模式的变化。但以上工作都未系统地研究裂纹在不同位置形核与扩展的影响因素,而裂纹形核位置的变化会影响到裂纹的合并从而影响涂层的寿命。
随着有限元技术的发展,内聚力单元法(CZM)和扩展有限元法(XFEM)被用于模拟裂纹的形成与扩展。CZM能有效模拟界面裂纹的扩展,XFEM能够动态地基于求解的方式,模拟裂纹的随机形核与扩展。二者相结合能够更有效地模拟裂纹在涂层中的扩展情况[12-14]。
为揭示TBCs裂纹的形成机理,探究不同TGO层尺寸和形貌对裂纹形核位置及其扩展规律的影响,本研究采用内聚力单元和扩展有限元法模拟界面裂纹的形核与扩展,分析不同TGO层初始厚度、粗糙度以及陶瓷层中不同初始裂纹对新裂纹形核位置及扩展规律的影响,为研究TBCs失效机理提供理论参考。
1 几何模型及材料参数
大气等离子喷涂(APS)热障涂层的制备过程中,各种因素的存在使TGO层的表面粗糙度大小不一,高温氧化使得TGO层厚度不均。本研究采用简化模型,考虑各层材料的高温蠕变以及粘结层的塑性,使用内聚力单元与扩展有限元方法对涂层裂纹形核与扩展进行计算。
1.1 几何模型
采用商用有限元软件ABAQUS建立经典的4层热障涂层系统,从上到下分别为陶瓷层(TC)、氧化层(TGO)、粘结层(BC)、镍基合金基底(SUB),如图 1所示。TGO 初始厚度为 1~4 μm,TC、BC、SUB厚度分别为 0.25、0.10、1.60 mm。采用正弦曲线来简化粗糙的TGO界面,通过保持波长不变而改变振幅来表征不同的TGO粗糙度,振幅为 3~6 μm,波长保持 40 μm不变。由于模型的周期性和对称性,采用半周期模型,在左边施加对称边界条件,右边添加MPC多点耦合约束,使右边节点在X方向上保持一致。假设初始为无应力状态,不考虑TC的高温烧结与相变应力,考虑各层材料的蠕变以及BC的塑性。有限元模型单元类型为耦合温度−位移单元(CPE4RT),模拟界面裂纹时采用内聚力单元(COH2D4)。
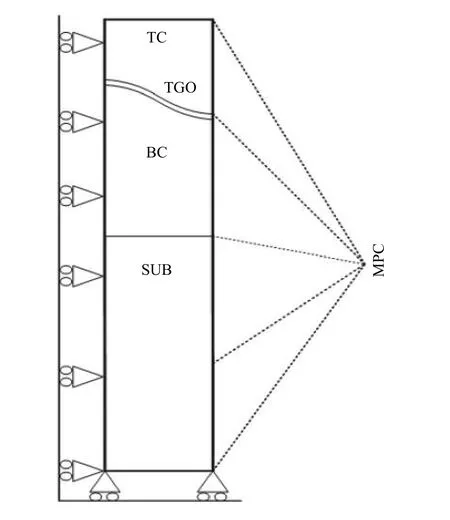
图1 热障涂层几何模型Fig.1 Geometric models of thermal barrier coatings
1.2 材料参数
温度极大地影响材料的蠕变性质。当温度大于600 ℃时,材料的蠕变影响涂层的性能[15-16],Lin等[17]对各层蠕变的数值研究表明,TGO层蠕变导致陶瓷层与粘结层的应力松弛,粘结层的蠕变会减小本层的应力但会增大陶瓷层的应力。在本研究模型中,假设各层为各向同性且均质材料。其中,SUB、TGO、TC层为弹−粘性材料,而BC为弹−粘塑性材料,其塑性参数如表1[18]所示。根据先前的研究,本研究选择诺顿幂率蠕变行为作为各层蠕变定律:
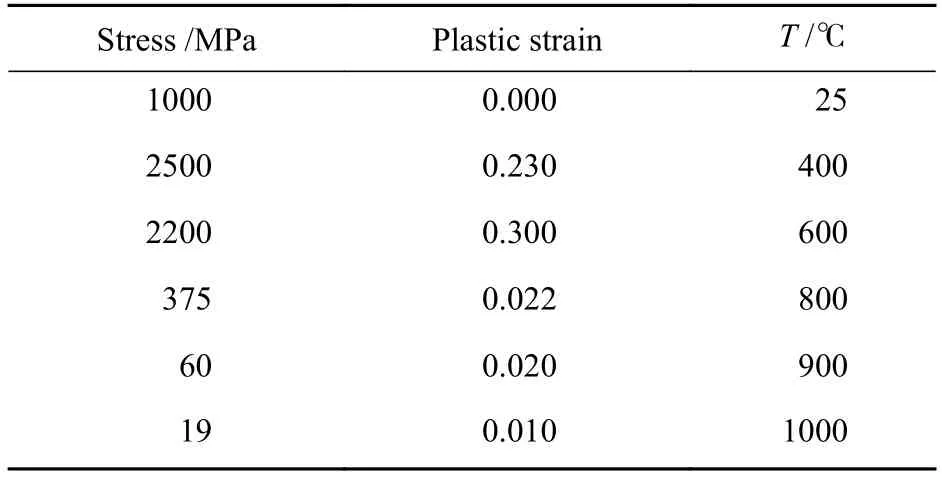
表1 粘结层塑性参数[18]Table 1 Plastic parameters of BC

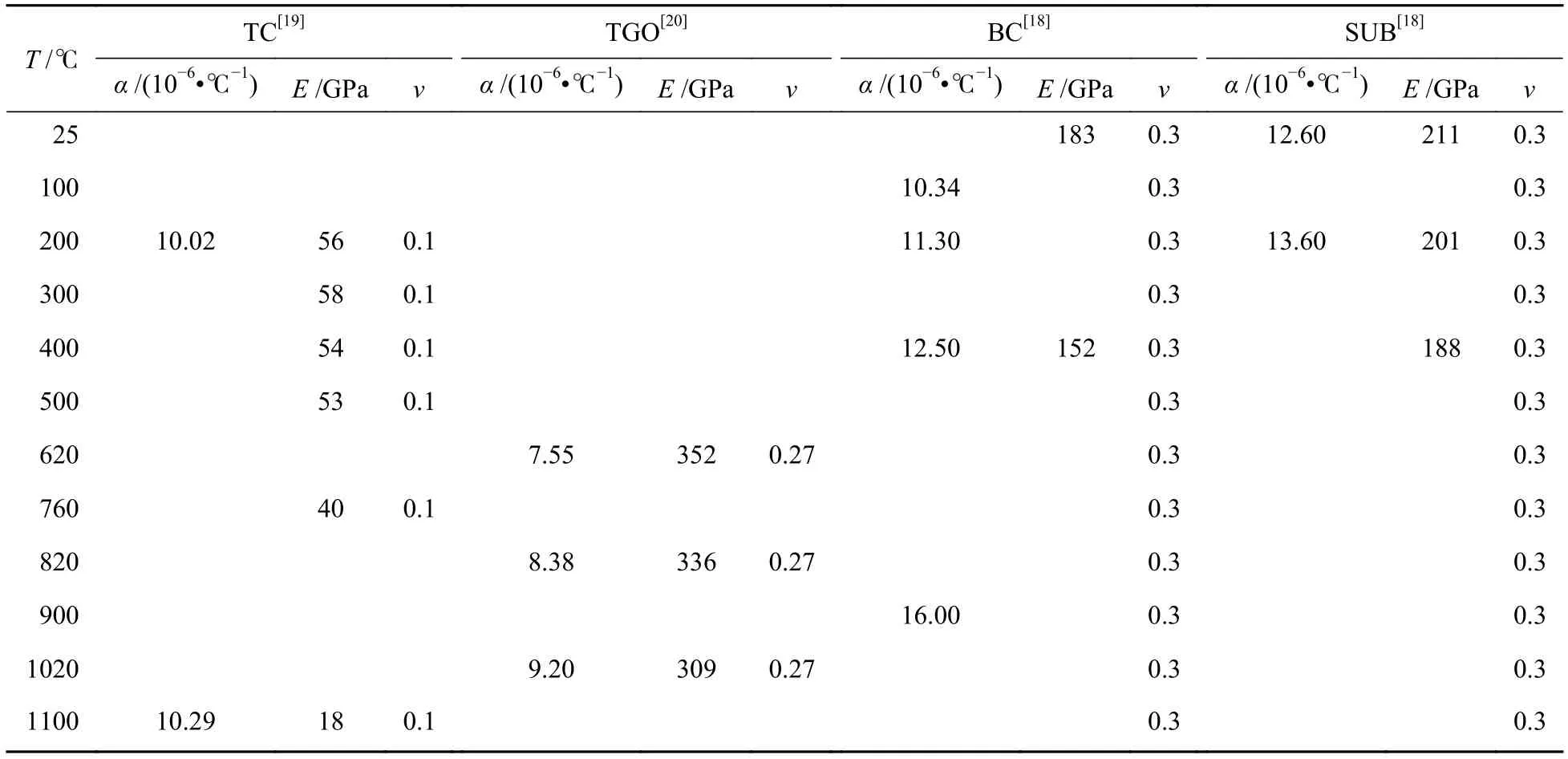
表2 各层基于温度的热膨胀系数、杨氏模量和泊松比参数Table 2 Thermal expansion coefficient, Young’s modulus and Poisson’s ratio of each layer
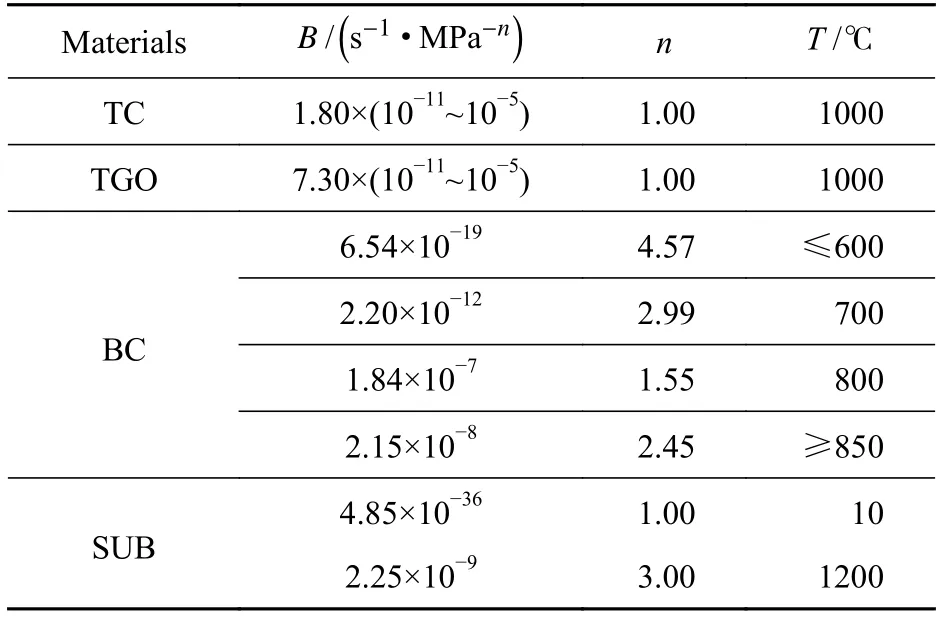
表3 蠕变参数[18]Table 3 Creep parameters
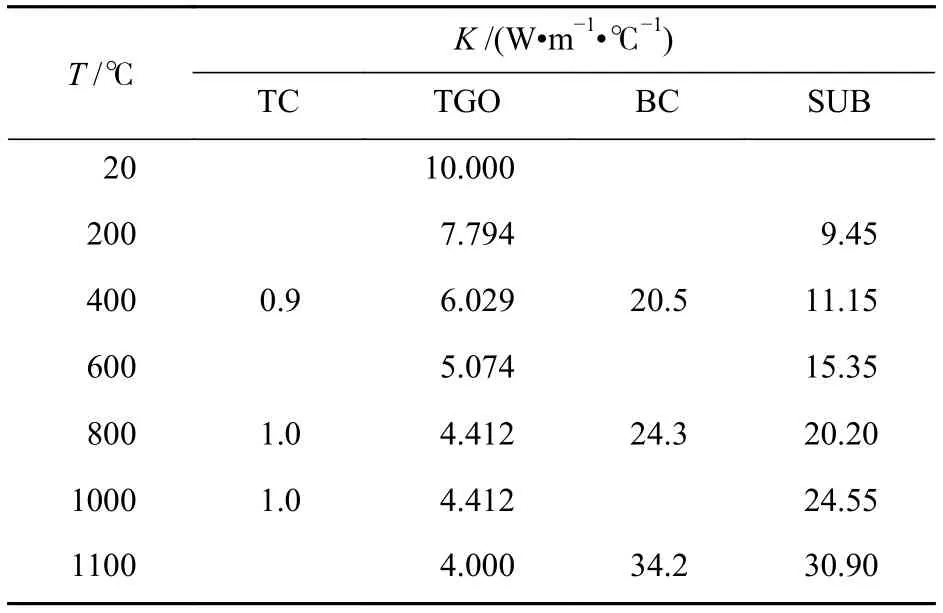
表4 各层热导率[19]Table 4 Thermal conductivity of each layer
考虑实际过程中的TGO生长为各向异性,本研究简化TGO的生长为横向生长和纵向生长。根据Evans等[3]的研究使用纵向和横向的生长膨胀比值为10,近似模拟高温氧化时TGO的生长[21]。
1.3 热循环载荷
为探究涂层承受一定数量的热循环载荷后,界面裂纹的形核与扩展情况,在涂层上下表面施加热循环载荷,温度曲线如图2所示。非均质热载荷施加在陶瓷层顶部与基底底部,通过对流换热对涂层施加热载荷,涂层上表面对流换热系数为 8 kW/(m2•K),涂层下表面对流换热系数为 2 kW/(m2•K)。
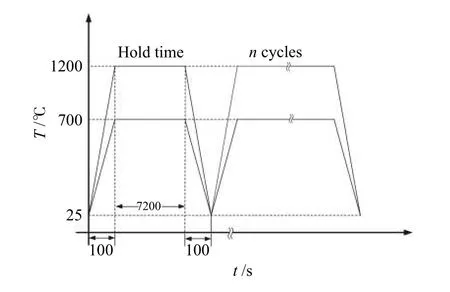
图2 热循环载荷Fig.2 Thermal cycle
2 内聚力单元模型
内聚力单元是基于内聚力模型的特殊单元,体现材料在粘结面处的牵引−分离(tractionseparation)本构关系[22-23],被广泛用于模拟材料内部的断裂与损伤,尤其在界面裂纹的研究上较为有效。图3为典型线性牵引−分离响应,模型假设最初为线弹性行为,当界面损伤达到界面强度时损伤开始(Di=0),随后单元按照线性软化直至完全损伤时(Di=1)单元去除。本模型选用二次名义应力准则,公式为:
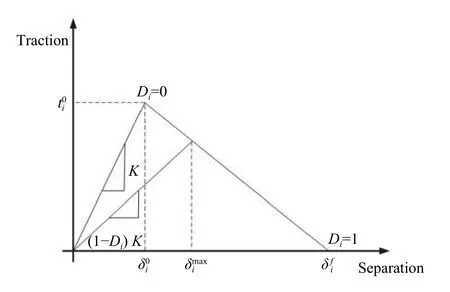
图3 牵引−分离损伤法则Fig.3 Law of traction-separation damage
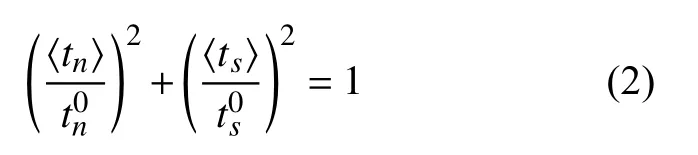
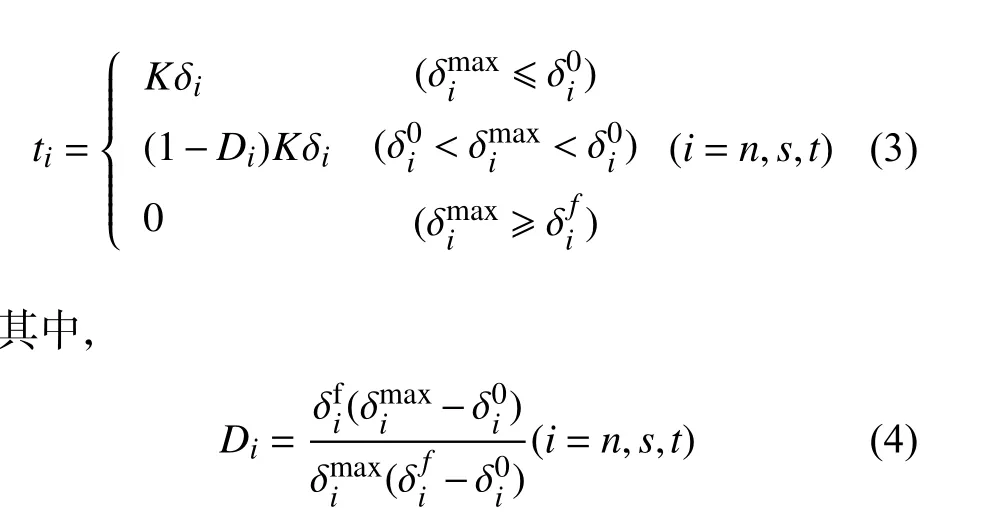
式中:t是牵引力,是分离位移,D是损伤因子,K是线弹性阶段的刚度,n、s、t分别代表垂直、平行、剪切方向,0、f代表损伤开始与结束,max表示当前阶段的位移最大值。
3 扩展有限元模型
由于传统有限元需要对裂纹尖端有足够细致的网格划分,在裂纹的扩展计算过程中需要重新划分网格,因此对模拟计算的软硬件要求极高,运算效率低下。Belytschko[25]在1999年首次提出扩展有限元思想,其基本思想为在形函数中加入描述裂纹的阶跃函数(Step function)和渐进场函数(Asymptotic function),用来描述裂纹的不连续性和裂纹尖端的位移场,所以XFEM可以在不指定预定义裂纹的情况下模拟裂纹的萌生。
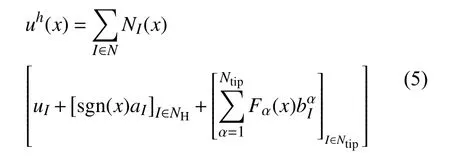
使用扩展有限元法对陶瓷层与氧化层进行无预定义路径来模拟任意基于计算结果的裂纹萌生与扩展,裂纹萌生与扩展按照牵引−分离法则。以往的工作主要是研究单一的TC裂纹扩展[24, 26],为了更接近涂层中陶瓷层多条裂纹的实际情况,本研究模拟陶瓷层多裂纹扩展,研究TGO层不同初始厚度、不同粗糙度以及陶瓷层初始裂纹对TBCs裂纹形核与扩展的影响。考虑到BC层为合金材料,应力松弛主要为塑性应变,因此假设BC层韧性足够而不发生开裂。在建立的有限元模型中,设置初始的状态为无应力,而TGO形态采用理想正弦曲线,有限元单元采用平面应变单元CPE4R,各层材料参数[27-28]如表2所示。由于TBCs的分层与裂纹的生长主要发生在TGO/TC界面,因此在TGO/TC界面使用内聚力界面方法(CIM)[26],如图4所示。内聚力界面刚度定义为109MPa/mm。内聚力界面的混合模式损伤演变选择基于能量的方式,选择线性的软化行为Benzeggagh-Kenane (BK) 断裂准则作为损伤演变准则。
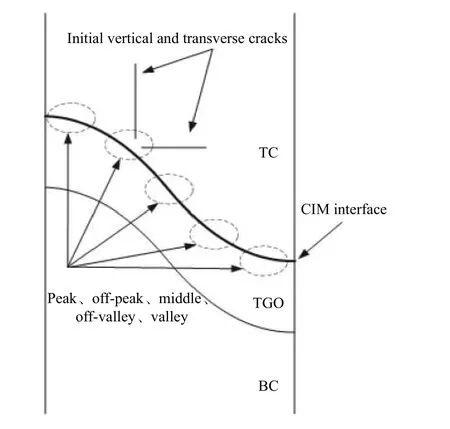
图4 内聚力界面及初始裂纹位置Fig.4 Cohesive interface and initial crack location
在TBCs的喷涂过程中,TBC/TGO界面的凹凸不平无可避免,在服役过程中由于TGO层的氧化生长也会造成界面形成不同的粗糙度,由此在界面引起的复杂应力分布对裂纹的萌生与扩展及涂层失效有重要影响[27-28]。为了研究TBCs系统裂纹的形核位置变化与扩展失效过程及其机理,提出采用内聚力单元与扩展有限元法分析TGO厚度、粗糙度以及TC初始裂纹对TGO/TC界面裂纹、陶瓷层内裂纹和氧化层内裂纹形核位置与扩展的影响。
在本研究中保持波长不变,通过振幅的大小来表征不同的粗糙度,在波长保持40 μm不变、TGO厚度h=5 μm时,分析TGO粗糙度从大变小(振幅 A 从 6 μm减小到 3 μm)时对 TC裂纹与TGO裂纹形核位置与扩展的影响。分析初始TGO厚度h从1 μm变化到4 μm时对TC裂纹与TGO裂纹形核位置与扩展的影响。
4 结果与讨论
4.1 TGO/TC界面裂纹的形核与扩展
当热障涂层为无初始应力及缺陷,TGO厚度与振幅均为5 μm的热障涂层在热循环载荷作用下,TGO/TC界面裂纹形核位置位于近波峰处,如图5所示。TGO/TC界面裂纹出现在TGO/TC界面的近波峰处,这说明裂纹容易在TGO/TC近波峰区域附近形核与扩展,近波峰处是裂纹形核的高概率区域,这也将为陶瓷层裂纹的形核埋下隐患,这与Song[21]、Jiang[24]等的研究结果一致。从图5可以看出,TGO/TC界面从波峰到中部处都发生了较大的损伤,近波峰处界面裂纹有向波峰与中部扩展的趋势,说明裂纹在近波峰处形核后将向两侧扩展,波峰与中部将是裂纹形核的下一个位置。
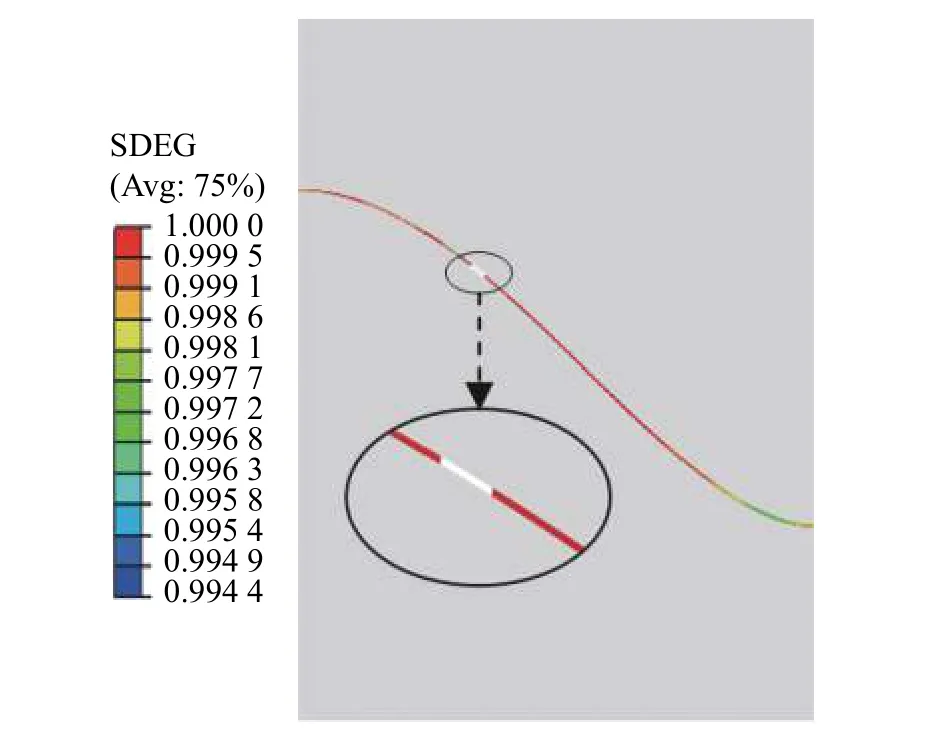
图5 基于内聚力单元的TGO/TC界面损伤示意图Fig.5 Damage of TGO/TC interface based on cohesive element
4.2 TGO初始厚度对TC裂纹与TGO裂纹形核位置与扩展的影响
图6为TGO振幅为 5 μm,初始厚度h分别为 1、2、3、4 μm 时,TGO裂纹与 TC裂纹形核及扩展的计算结果。从图中可以明显看出,当TGO初始厚度为1 μm时,TC裂纹在TGO/TC界面波峰处形核并扩展,但随着TGO初始厚度的不断增加,TC裂纹形核位置不断下移至近波峰处,而TC裂纹的扩展长度没有明显的变化。
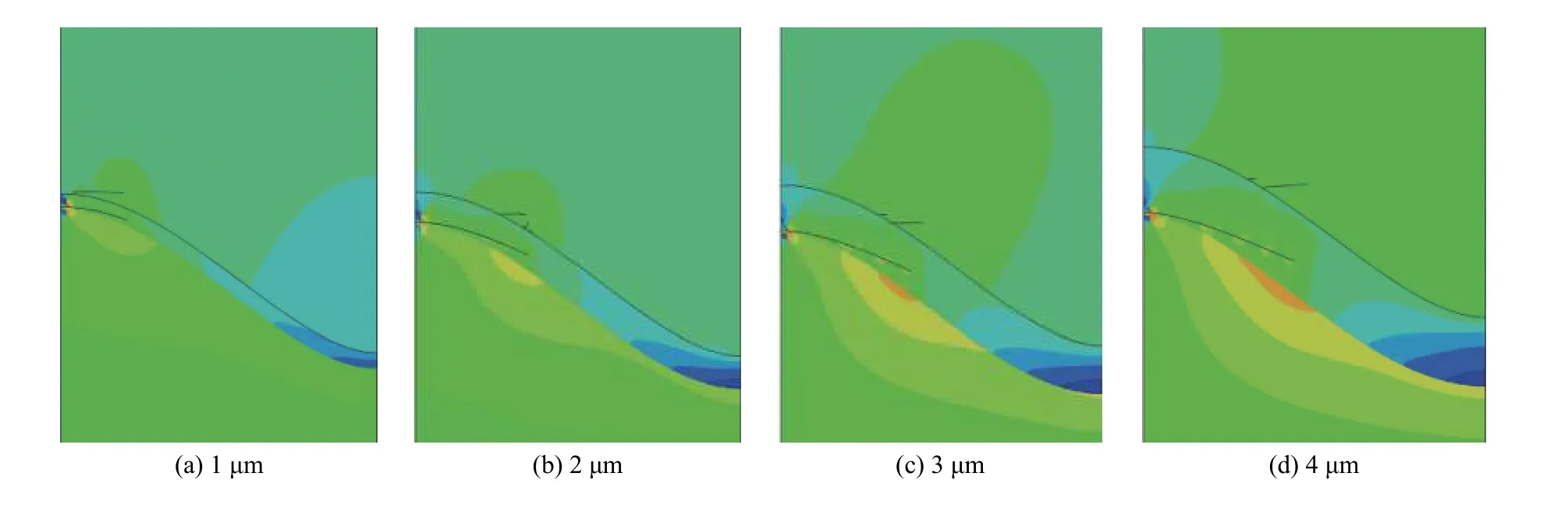
图6 不同初始厚度的TGO裂纹与TC裂纹形核位置及扩展Fig.6 Nucleation location and propagation of TGO cracks and TC cracks with different initial thickness
这里要指出的是,损伤初始准则采用最大主应力准则,所以将最大主应力用于之后热障涂层从1000 ℃冷却到20 ℃时的应力分析及陶瓷层与氧化层裂纹的萌生与扩展。这可以从图7中TGO/TC界面处最大主应力分布来解释,图中在波峰处(即峰谷归一化距离为0~0.2范围内)最大主应力从压缩应力急剧变化到拉伸应力,且TGO的h越小,应力变化越剧烈。当TGO的h=1 μm时,在波峰处拉伸应力值达到开裂的临界强度,TC裂纹在波峰处形核与扩展,所以在图7中,h=1 μm时,界面最大主应力在波峰处由于TC裂纹的形核导致波峰处开裂位置的应力集中得到释放而产生向下的突变应力;当h=2~4 μm时,拉伸最大主应力在近波峰处达到临界开裂强度,故应力在近波峰处向下突变。在图6中,TGO裂纹形核位置都出现在TGO/BC界面的波峰处,这个结果与Kyaw等[26]的结果一致。对于TGO裂纹的扩展长度,随着TGO初始厚度变大,TGO裂纹长度增加了接近6 μm(图8),这是因为初始TGO厚度的增加导致TGO内产生较大的失配应力,从而促进TGO裂纹的扩展。因此,TGO厚度的增加将促使TGO层内裂纹的扩展,使TGO裂纹与TC裂纹合并贯穿,导致涂层剥落失效。
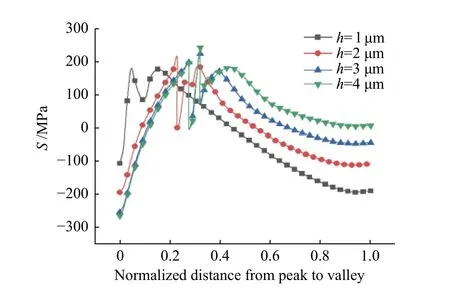
图7 TGO/TC界面最大主应力S随TGO厚度h的变化Fig.7 Variation of the maximum principal stress at TGO/TC interface with the thickness of TGO
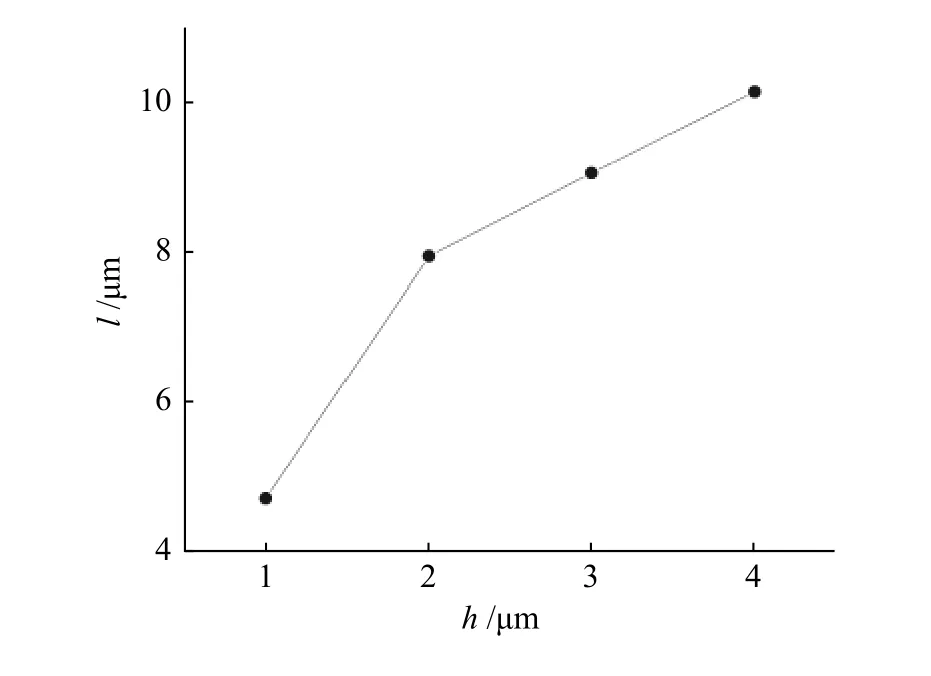
图8 TGO 裂纹长度 l随 TGO 初始厚度 h的变化Fig.8 Crack length of TGO varies with the initial thickness of TGO
4.3 TGO粗糙度对TC裂纹与TGO裂纹形核位置与扩展的影响
在图9中,TGO厚度为5 μm,当TGO粗糙度逐渐减小时(振幅 A 从 6 μm 减小至 3 μm),TC 裂纹形核位置从近波峰逐渐向中部转移,最终TC裂纹被抑制,而TC裂纹的扩展长度没有较大的变化。当振幅A为5、6 μm时,TC裂纹萌生在近波峰(图 9a、图9b);当振幅 A为4μm 时,TC 裂纹形核位置出现在中部及近波峰;当振幅A为3 μm时,TC裂纹被抑制未出现裂纹。
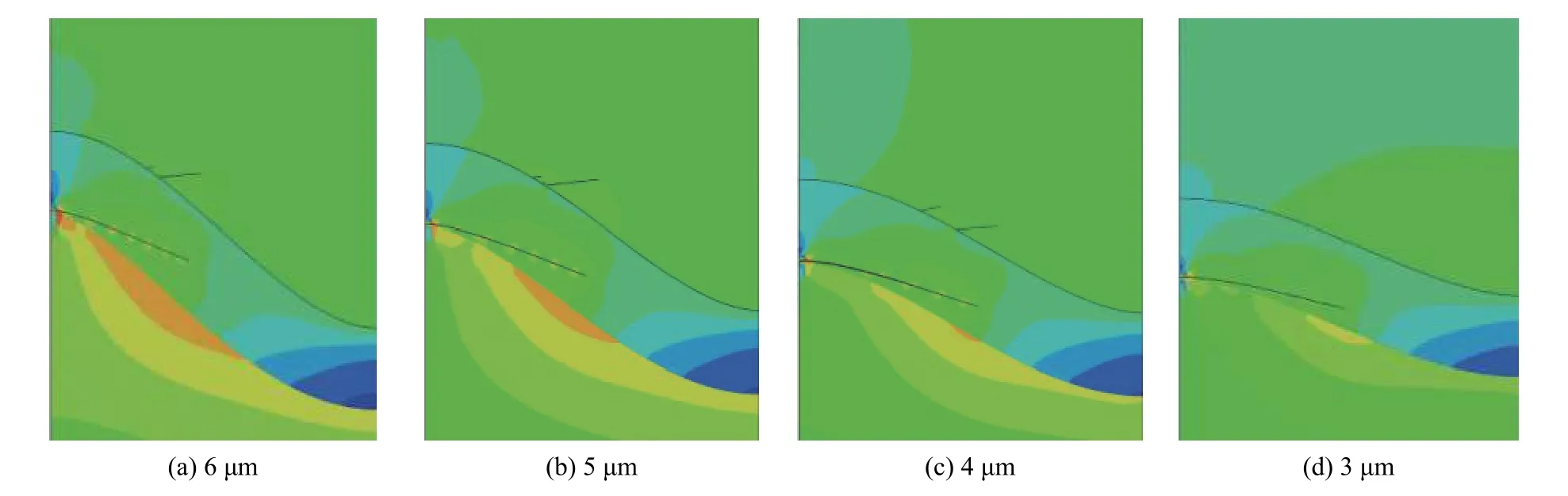
图9 不同振幅时TGO裂纹与TC裂纹形核位置及扩展Fig.9 Nucleation location and propagation of TGO cracks and TC cracks at different amplitudes
这在图10中可以得到解释,图中随着粗糙度的降低,TGO/TC界面波峰到近波峰处(峰谷归一化距离0~0.4)最大主应力的斜率变化逐渐变小,应力变化更迟缓。当TGO振幅A为5、6 μm时,最大主应力在波峰到近波峰处从压应力快速转变为拉应力,在近波峰处达到临界开裂强度,从而导致裂纹形核并扩展,在此过程中,应力得到释放,使最大主应力向下突变;当TGO振幅A为4 μm时,最大主应力在近波峰与中部(峰谷归一化距离0.2~0.6)达到临界开裂强度,因此裂纹在此形核并扩展,而最大主应力向下突变;当TGO振幅A为3 μm时,最大主应力从波峰至中部变化缓慢,且最大主应力峰值小于临界开裂强度,所以图中并没有出现由于裂纹产生与扩展而导致的应力向下突变。
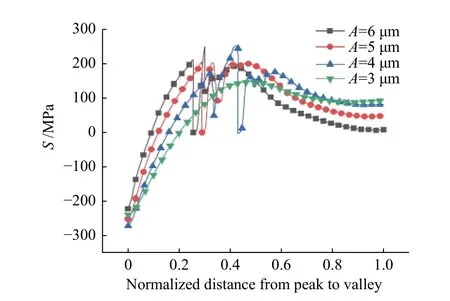
图10 TGO/TC界面最大主应力S随TGO粗糙度的变化Fig.10 The variation of the maximum principal stress of TGO/TC interface with TGO roughness
因此,较小的TGO粗糙度能降低TGO/TC界面处波峰到中部范围内的拉应力水平,使TC裂纹形核位置由近波峰向中部转移。随着粗糙度的进一步减小, TGO/TC界面处的拉应力都将小于临界开裂强度,从而使TC裂纹无法形核(图9d)。所以,较小的TGO粗糙度能在一定程度上抑制TC裂纹的形核与扩展,而较大的TGO粗糙度会使TC裂纹在近波峰与中部位置形核并扩展。
综上所述,降低TGO界面粗糙度能有效降低TGO/TC界面处的应力水平,从而抑制TC裂纹的形核与扩展,防止涂层过早开裂剥落失效。随着TGO粗糙度减小(振幅 A由 6 μm 降低到 4 μm),TGO裂纹长度逐渐增加,但当TGO粗糙度继续降低至振幅A为3 μm时,TGO裂纹长度并没有继续增加,原因是由于TC内的裂纹对TGO裂纹扩展产生了影响(图11)。由于粗糙度的降低使TC裂纹被抑制后,TGO裂纹的扩展也受到了抑制,这在4.4节中可以得到进一步验证。
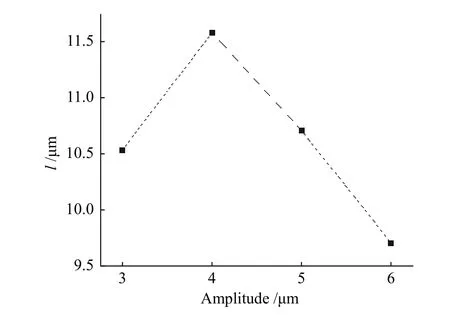
图11 TGO 裂纹长度 l随 TGO 粗糙度的变化Fig.11 Variation of TGO crack length with TGO roughness
4.4 初始裂纹对TC裂纹形核位置与扩展的影响
当在TGO/TC界面近波峰处预置初始横向裂纹(图4),分析初始TC内横向裂纹长度对TGO裂纹扩展的影响。模拟结果如图12所示,TGO裂纹扩展长度与初始横向TC裂纹长度正相关。当TC裂纹扩展被抑制时(图9d),TGO裂纹的扩展也受到抑制。这也验证了4.3节中由于粗糙度的降低,TC裂纹被抑制后TGO裂纹的扩展也受到了抑制的结论(图11)。由于TGO/TC界面近波峰处是裂纹形核与扩展的高危区,因此抑制近波峰处TC裂纹的形核与扩展对于提高热障涂层寿命、预防涂层过早剥落失效有重要意义。Lu等的研究结果也验证了竖直裂纹能有效提高涂层的应变容限与热稳定性,阻止横向裂纹的扩展[29-30],所以当在近波峰处预置一条初始竖直裂纹时(图13a),TGO/TC界面近波峰处的TC裂纹被抑制,但TC裂纹仍然在中部形核与扩展;当在近波峰与中部同时预置初始竖直裂纹时,TGO/TC界面处TC裂纹被完全抑制(图13b);当竖直裂纹与TGO/TC界面的距离逐渐增大时,TC裂纹逐渐开始形核且向着竖直裂纹的尖端扩展最终与竖直裂纹合并且不再继续扩展(图13c、图13d)。所以,单一的竖直裂纹会使裂纹形核位置的发生改变,从而达不到抑制裂纹形核的效果,在TGO/TC界面近波峰与中部同时预置初始竖直裂纹能更有效低抑制裂纹的形核与扩展。当距离TGO/TC界面越远,竖直裂纹对TC裂纹的形核抑制越弱,但竖直裂纹能有效地阻挡TC裂纹的进一步扩展。
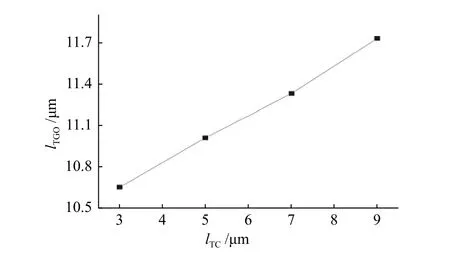
图12 TGO裂纹长度随初始横向TC裂纹长度的变化Fig.12 Crack length varies with the initial transverse crack length
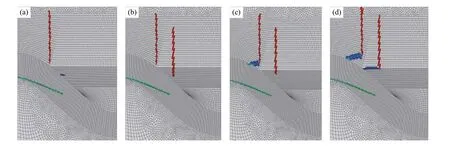
图13 竖直裂纹对裂纹形核与扩展的影响Fig.13 Effect of vertical cracks on crack nucleation and propagation
5 结论
1)在热循环载荷作用下,TGO/TC界面的近波峰处容易形核并向波峰及中部扩展,从而导致裂纹合并而引起热障涂层失效。
2)随着初始TGO厚度的增大,TGO裂纹长度明显增大且TC裂纹形核位置从波峰转向近波峰;随着TGO粗糙度的减小,TC裂纹形核位置从近波峰向中部转移。当粗糙度进一步减小后,TC裂纹和TGO裂纹的扩展都将受到抑制。
3)单一的初始竖直裂纹会导致裂纹形核位置的转移,而近波峰及中部同时预置初始竖直裂纹能有效地抑制裂纹形核与扩展。所提出应用内聚力单元与扩展有限元模型为热障涂层微裂纹失效机理提供了理论基础和数据支撑。
