导数在实际生活中的应用举例

张倩瑶，黄 星

(南阳职业学院，河南 南阳 474500)

在生产实际和科学技术中，为了在一定条件下提高生产效率、降低成本、节约原料，常常需要调整方案，使方案最优化，这时就会应用到导数知识，最大限度地节约人力、物力，以取得最好的效果。最优化问题的最简单类型是求目标函数的最大值和最小值。

1 基础知识

函数的最大(小)值会随着其定义域的不同而差别较大。由已知定理可知，闭区间上的连续函数一定有最大值和最小值，这是存在定理，并没有提供求法。而函数在闭区间[a，b]上的最大(小)值是指在整个区间上的所有函数值的最大(小)者，因而最大(小)值是全局性概念。和极值不同，极值只是函数在一点的某个领域内的最大(小)值，极值是一个局部性概念。但若函数在区间内部的一点达到最大(小)值，那么这个最大(小)值同时也是极大(小)值。此外，函数的最大(小)值还有可能存在于区间的端点，因此，求闭区间(a，b)上连续函数f(x)的最大值和最小值的一般步骤如下：

(1)找出(a，b)内f(x)的所有驻点和导数不存在的点，设为x1，x2，…，xn；

(2)比较f(a)，f(x1)，f(x2)，…，f(xn)，f(b)；

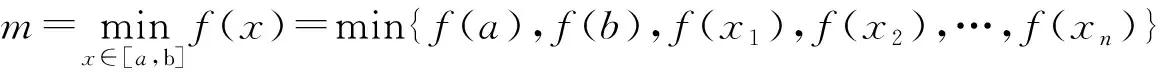
2 最大值和最小值应用问题举例

例1：铁路线上AB段的距离为100 km，工厂C距A处20 km，AC垂直于AB(如图1所示)。为了运输需要，要在AB线上选定一点D，从D向工厂C的方向修筑一条公路。已知铁路上每吨千米的货运费用与公路上每吨千米的货运费用之比为3：5，为了使货物从供应站B运到工厂C每吨货运的总费用最省，问D点应选在何处？

图1Fig.1

注意：在实际问题中，若函数f(x)在其定义域内只有一个可能极值点x0(驻点或导数不存在的点)，而实际问题本身又知f(x)在定义域内一定有最大(小)值，则f(x0)即为最大(小)值。

例3：欲建一座底面是正方形的平顶仓库，设仓库容积是1 500 m3，已知单位面积仓库的造价是四周墙壁造价的3倍，求仓库底的边长和高，使总造价最低。

解：设底边长为x米，高为y米，墙壁造价q元/m2，总造价为ω元。

3 结语

通过求导的方法能够解决实际生活中的最大值和最小值问题，使问题更简单化，易于人们理解，具有实际意义。