波叠加法解的非唯一性问题改进及声源位置优化研究

夏雪宝，向 阳，张 波，程 鹏

（1.广州广电计量检测股份有限公司，广州 510000；2.武汉理工大学能源与动力工程学院，武汉 430063）

0 引 言

目前，边界元（BEM）的方法广泛用于任意形状结构的声辐射问题求解，但在求解计算时需对奇异积分进行数值处理，且当遇到会产生非唯一性问题的积分时，对奇异积分的数值处理会更加困难[1-3]。为避免声学求解时遇到的奇异积分问题，Koopmann 等[4]提出一种可避免奇异积分的声场求解方法——波叠加法，该方法是将若干虚拟简单源（单极子源）置于辐射体内部光滑曲面上，通过给定的速度边界条件求得声源的源强后，线性叠加虚拟简单源的辐射声场以获得辐射体的声场解。

采用波叠加法求解时，单极子源均匀置于辐射体内部封闭光滑曲面上，其位置对计算的精度有很大影响[5]。由于单极子源位置为光滑封闭的曲面，当分析波数等于或接近内部Dirchlet 条件对应的特征波数时，就会出现解的非唯一性问题。针对波叠加法解的非唯一性问题，文献[6]采用三极子源（单极子与偶极子组合）可有效解决非唯一性问题，但由于简单源变为三极子，使得计算效率降低。文献[7]将单极子源所在光滑曲面到辐射体中心点的矢径模值取为复数，也能保证声场解的唯一解，但由于矢径模值的取值凭经验选取，计算精度较难保证。

CHIEF 法（Combined Helmholtz Integral Equation Formulation）是一种改进的声辐射边界元法[8]。该方法通过在辐射体内部增加若干CHIEF点，联立这些点处与边界表面节点的Helmholtz积分方程[9]，可有效保证声场的唯一解。文献[10]提出一种用于求解声场问题的基本解方法MFS（Method of Funda⁃mental Solutions），该方法通过叠加一组辐射体内部随机布置的声源声场以获得辐射体结构总的声场解，数值算例表明该方法亦可保证全波数域内声场的唯一解，但需对声源位置进行优化以保证声场解的计算精度[11]。

本文基于CHIEF 法和基本解法（MFS）的思想及前期研究成果[12]，通过在辐射体内部添加额外的单极子源（称为附加源）来保证声场的唯一解。波叠加法计算结果的总体精度与辐射体表面速度重构密切相关。Koopmann 对比了配置点法、最小二乘法及体积速度匹配法，指出采用体积速度匹配对重构表面速度边界条件及计算辐射声场具有最优的精度[13]。因此本文采用附加源波叠加法求解辐射声场，以重构后体积速度相对误差为目标函数，获取单极子源的最优位置，算例表明，该方法的声场计算精度满足需求。

1 波叠加法及解的非唯一性

如图1所示，波叠加法计算时，通过叠加N个辐射体内部光滑曲面上声源的辐射声场，可得到表面S外部空间场点的声压为[13-15]

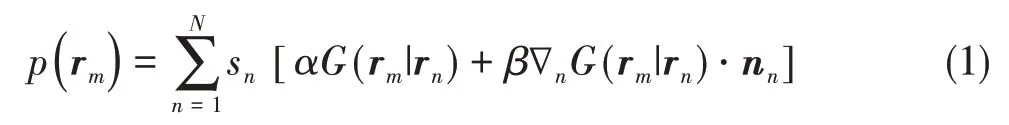
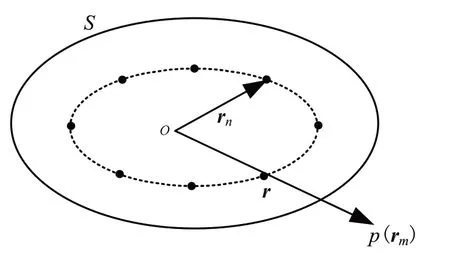
图1 波叠加法声源位置示意图Fig.1 Monopole source location of wave superposition method

式中，sn为等效声源强度；G(rm|rn)= eikR/R为自由空间格林函数[12]；rn和rm分别为声源点及空间场点位置向量；R为声源点rn与空间场点rm之间的距离；i为虚数单位；k为波数；∇n为对声源点求梯度；nn为偶极子声源单位法向量。α= 1，β= 0时表示声源为单极子源；α= 0，β= i/k表示声源为偶极子源。

理想流体介质（空气）质点速度与声压关系为v(rm)=∇p(rm)/ikρc，因此由式（1）可得

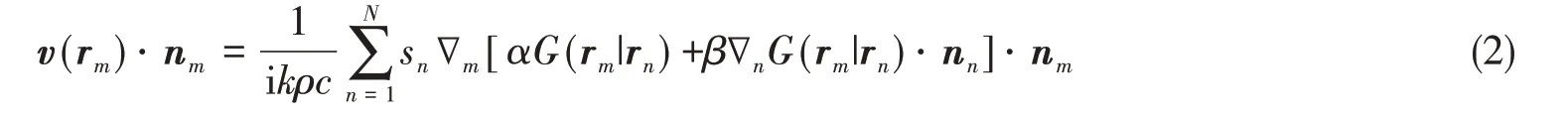
式中，ρc为空气特性阻抗；nm为边界表面位置单位法向量；∇m为对边界表面质点求梯度。对式（2）两边进行积分，可得辐射体边界表面单元的体积速度为

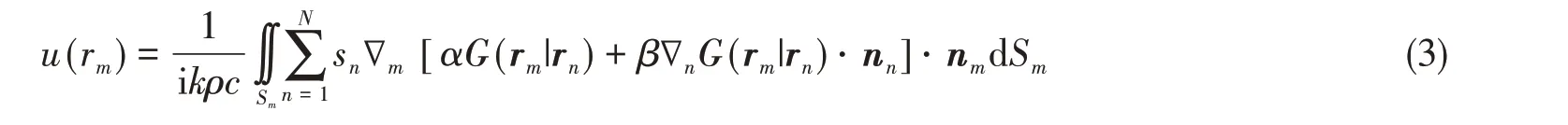
式中，Sm为表面单元m的面积区域。式（3）可用矩阵的形式表示为

式中，u、s分别为体积速度向量及声源强度向量。矩阵U中的元素为

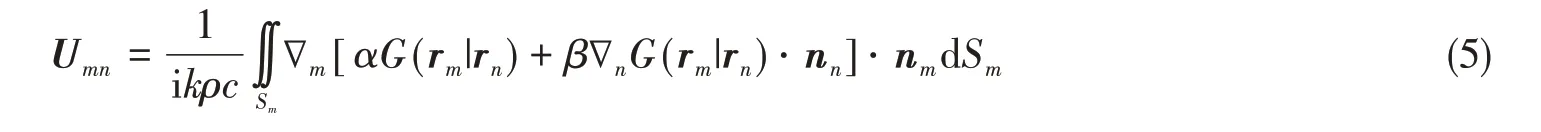
由式（1）可知，α、β的取值决定了波叠加法声源类型。文献[16]指出：当等效声源为单极子源或偶极子源时，波叠加积分方程的分析波数为内部Dirichlet条件或Neumann 条件所对应的特征波数，声场均会出现解的非唯一现象；而采用三极子波叠加法时，特征波数不会等于或接近内部Robin 条件对应的特征波数，该方法可以保证全波数域声场解的唯一性。

2 附加源波叠加法

波叠加法相比基本解法（MFS）的不同之处在于前者将声源置于辐射体内部光滑曲面上，而非在辐射体内部任意放置。CHIEF 主要思想是通过在辐射体内部添加额外点与边界表面联立积分方程来保证声场解的唯一性。因此，基于CHIEF 法和基本解法（MFS）法的思想，通过在辐射体内部添加若干个额外的单极子源来保证分析波数域内声场的唯一解，添加的额外单极子源称为附加源，如图2 所示，相应的声场解为

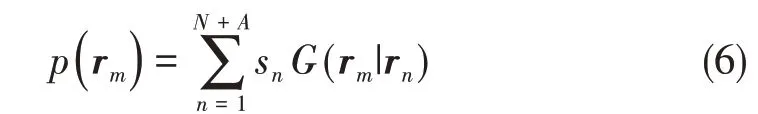
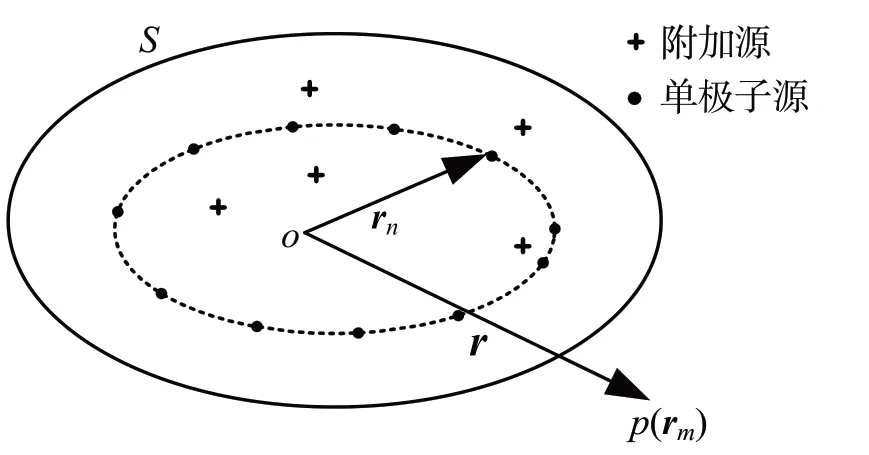
图2 单极子源及附加源位置示意图Fig.2 Monopole source and additional source location of wave superposition method

式中，A为附加源的个数。为发挥附加源的作用，附加源的位置要避免与单极子源所在光滑曲面重合。声场整体求解精度仍取决于辐射体内部光滑曲面的位置及单极子源数量N，因此需对单极子源的数量及位置进行优化选取，以确保声场计算的精度及效率最优。

3 声源位置优化计算

波叠加法计算时，为保证速度边界条件能精确地被虚拟单极子源等效，可通过给定的速度边界条件求得声源的源强后，对辐射体表面的体积速度进行重构，对比重构前后体积速度的相对误差。因此，本文以重构前后体积速度的相对误差为目标函数，对结构辐射体内部单极子源所在曲面位置进行优化。表面离散为N个声学网格辐射体的表面体积速度相对误差定义为

式中，u1,i为结构辐射体表面单元i重构后的体积速度，u0,i为给定或已知的表面单元i的体积速度。

实际采用波叠加法求解过程中，一定范围内增加单极子源个数可提高声场求解计算的精度，但单极子源个数过多时，单极子之间距离过近会导致计算精度降低，同时声源数量过多会使得计算效率降低。通过建立边界网格模型，确保表面边界单元尺寸小于λ6（λ为声波波长）以确定简单声源数量。而辐射体内部声源所在曲面位置则可通过对结构表面单元网格节点缩小得到。

本文采用附加源波叠加法计算声场时，以分析波数范围内重构前后体积速度相对误差为目标函数，以同形缩小系数为优化变量对声源所在曲面位置进行优化。优化的数学模型为

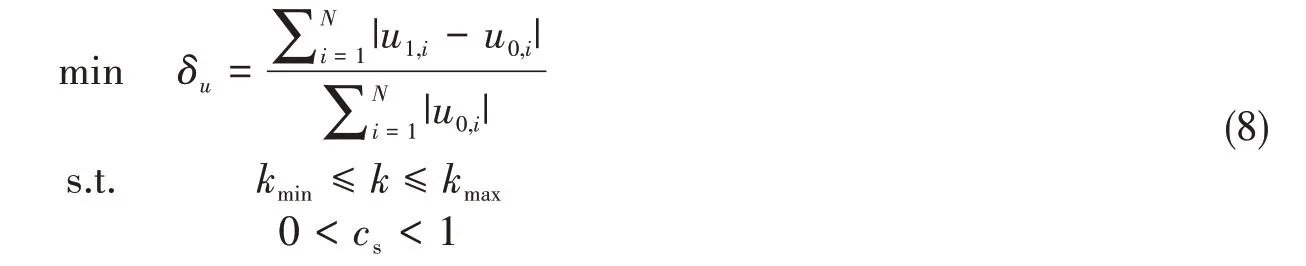
式中，k为分析波数；cs为同形缩小系数。缩小系数cs的取值范围不能过大或过小，缩小系数cs过大或过小时，单极子源分别距结构表面节点或单极子源相互之间距离过近，导致积分计算时计算精度低。由于cs范围小，实际优化计算时，可以采用遍历法得到最优cs。因此，本文采用改进的源波叠加法优化计算流程为：第一步，将辐射体表面划分为声学网格，确定单极子源个数；第二步，以重构前后体积速度相对误差为目标函数，优化得到最佳缩小系数cs，确定最优声源位置；第三步，添加适量附加单极子源来保证分析波数范围内声场的唯一解。

4 数值算例

4.1 脉动球源

4.1.1 单极子波叠加法球心位于坐标原点的脉动球源声场解析解为[3]

式中，r为坐标原点与空间场点间的距离，v为表面振速幅值，a为半径。现假设a=1 m，v=1 m/s，在球源内部半径为0.5 m（b=0.5a）的球面上均匀添加59 个单极子源。采用单极子波叠加法及解析解分别求解坐标（0 m，0 m，1 m）处声压，声压实部与虚部计算结果如图3 所示，分析波数范围为0～20，步长为0.01。

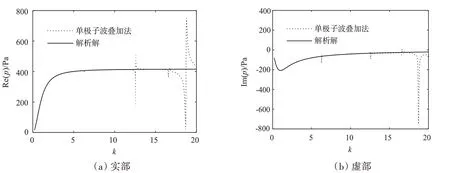
图3 采用单极子波叠加法及解析解求得不同坐标处声压对比Fig.3 Comparison of sound pressures at different coordinates by monopole sources wave superposition method and analytical solution

由图3 可知，单极子声源所在曲面为b=0.5a内部球面时，特征波数处（kb= π,2π,3π…）声场会出现解非唯一性问题，其它波数处声场解精度较高。

4.1.2 附加源波叠加法

采用改进的波叠加法（附加源波叠加法）进行计算时，在4.1.1节基础上，于坐标（0 m，0 m，0 m）处即坐标原点添加一个单极子源，计算结果如图4所示。

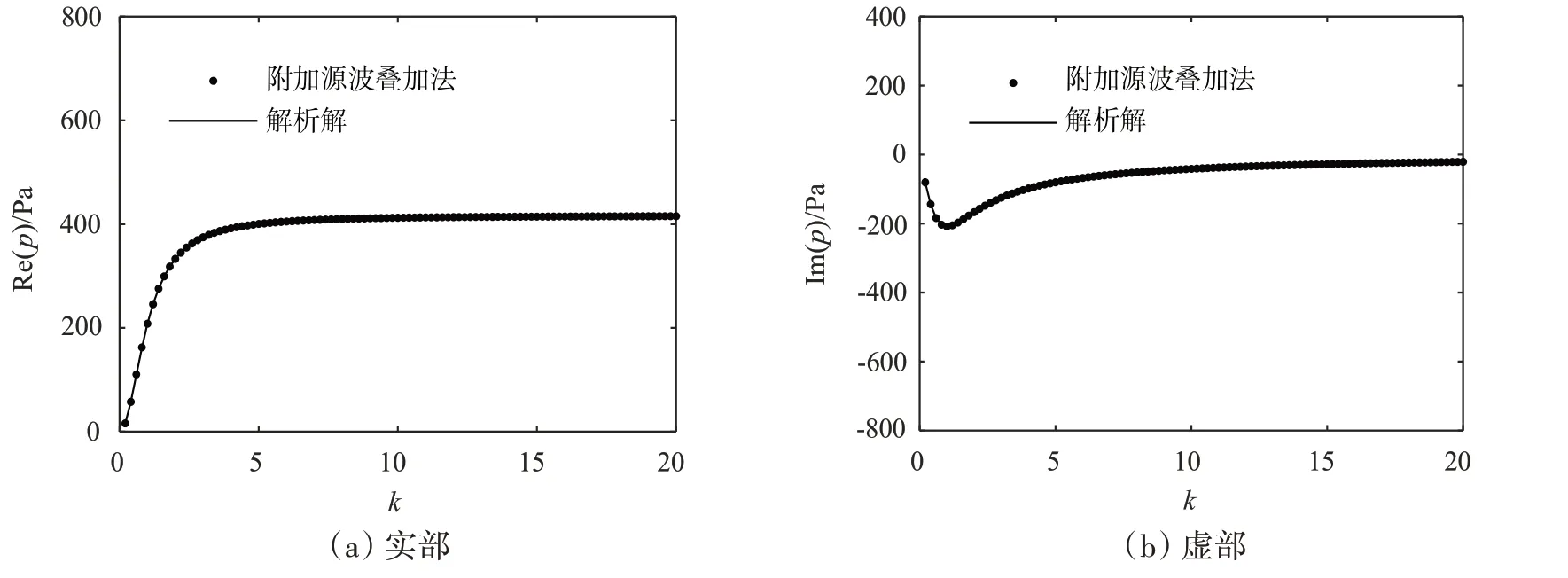
图4 采用附加源波叠加法及解析解求得不同坐标处声压对比Fig.4 Comparison of sound pressures at different coordinates by additional sources wave superposition method and analytical solution

由图4可知，脉动球源中心处添加一个单极子源求解的表面声压与解析解完全一致，有效克服了声场解的非唯一性问题。

4.1.3 计算耗时及计算精度对比

对比附加源与三极子波叠加法的计算耗时和精度，以上述脉动球源为例，分别求解脉动球源表面声压相对误差以及计算所需时间，其中表面声压相对误差定义为

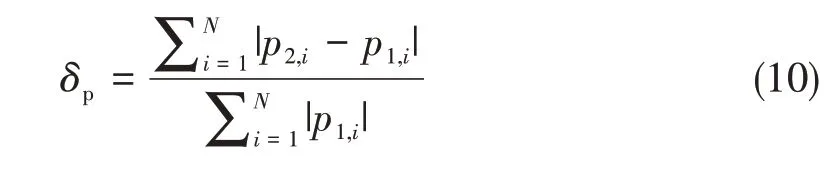
式中，p1,i为声压解析解，p2,i为声压数值解，N为辐射体表面节点个数。计算结果如图5所示。

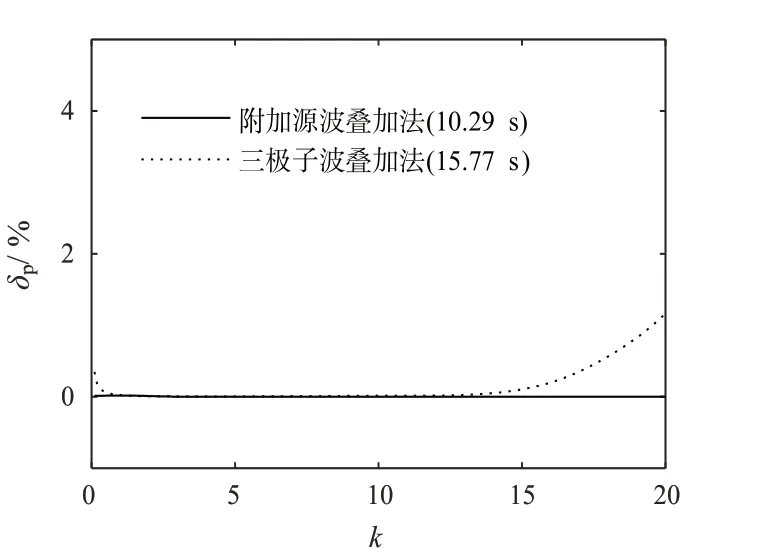
图5 表面声压相对误差及计算耗时Fig.5 Relative error of surface pressure and computing time

由求解的表面声压相对误差结果可知，附加源波叠加法计算误差几乎为0，相应的计算时间仅为三极子波叠加法的50%左右。

4.2 复杂几何体

如图6 所示，以总包络尺寸1.5 m × 1m × 1m 复杂几何结构体为对象，建立该结构的边界元模型（表面共有600 个单元）。波叠加法计算时，该模型的单极子源位置由该结构表面单元中心位置坐标缩小后得到。表面速度边界条件及表面标准声压则由位于该几何体中心坐标原点处的简单源产生。

图6 复杂几何结构体边界元网格模型Fig.6 Boundary element model of complex volume

采用单极子波叠加法求解不同缩小系数cs时体积速度相对误差，分析不同cs时对应声场解的非唯一性问题。cs的范围为0.4～0.85，步长为0.01，分析的波数为0～20，步长为0.01。计算的结果如图7所示。

由图7 可以得出，不同的cs对应的特征波数点不一致，且无规律可循，图中的尖峰或亮点为对应的特征波数。从图中颜色分布可以看出，表面体积速度相对误差随cs呈两头大、中间小的趋势。由于特征波数处存在解的非唯一性问题，因此不能采用分析波数范围内体积速度相对误差的总和或均值对计算精度进行评判，进而确定最优的cs值。

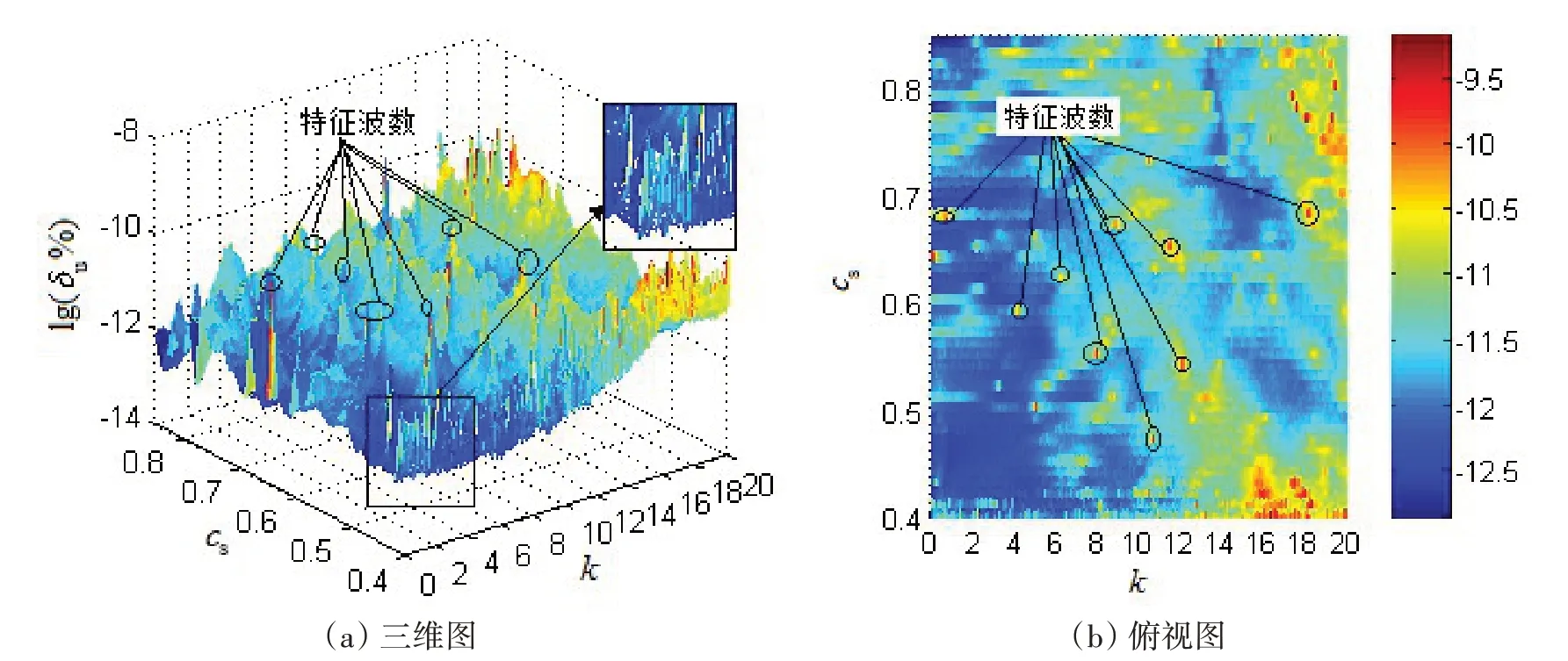
图7 体积速度相对误差Fig.7 Relative error of volume velocity

本文通过平均值法计算体积速度相对误差俯视图的灰度矩阵，再统计分析各cs值下灰度总值趋势，进而确定最优cs值，结果如图8 所示。由图8 可得出，cs= 0.62 时，体积速度相对误差灰度总值最小，即为计算精度的最优解。灰度总值趋势与体积速度相对误差分布一致，呈现两头大中间小的趋势。

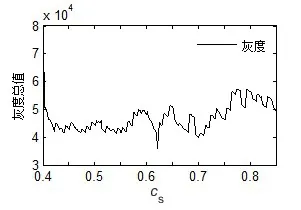
图8 体积速度相对误差灰度趋势曲线Fig.8 Gray scale distribution curve of the volume velocity relative error

确定最佳cs值以后，采用附加源波叠加法对该模型进行计算，以克服声场在k=6.21处解的非唯一性问题。确定缩小系数cs= 0.62 后，添加了5 个附加源的计算结果如图9 所示，复杂几何体内部添加的5个单极子源位置由软件随机确定，且经对比计算发现数量为5时效果最好。由图9可知，cs= 0.62时，5 个附加源可有效解决复杂几何体声场特征波数（k=6.21）处解的非唯一性问题；同时整体计算误差lg(δp%) < 0 即δp% < 1，计算精度非常高，说明以体积速度相对误差为目标函数优化得到最佳cs值满足计算精度要求。

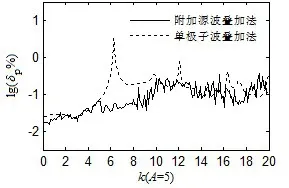
图9 表面声压相对误差Fig.9 Relative error of surface pressure

5 结 语

对应复杂几何体，波叠加法计算时以表面体积速度相对误差为目标函数，优化得到最佳单极子源位置，再通过辐射体内部添加适量额外的单极子源可有效保证声场的唯一解，且满足计算精度需求。但对如何优化确定附加源的数量及位置，以保证全波数域声场的唯一解有待后续进行深入的研究。