无轴轮缘推进器电机与水力部件耦合优化设计研究

蒋 寒，盛晨兴，欧阳武

（1.武汉理工大学能源与动力工程学院，武汉 430063；2.船舶动力工程技术交通行业重点实验室，武汉 430063；3.国家水运安全工程技术研究中心可靠性工程研究所，武汉 430063；4.中船动力研究院有限公司，上海 201306）

0 引 言

无轴轮缘驱动推进器（shaftless rim-driven thruster，RDT，也称为集成电力推进器，简称无轴推进器）是由一个同步永磁电机、螺旋桨、导管和轴承等组成，如图1（a）所示。电机围绕着螺旋桨，并集成到导管中；电机的定子嵌入到导管中，转子围绕着螺旋桨形成一个圆环；轴承通常布置在轮缘两侧，嵌入到导管中。整个推进器淹没于水下，通过电缆连接到船上发电装置。这种推进系统可节省舱室空间，减少振动和噪声，提高推进效率[1]。无轴轮缘推进器实体结构如图1（b）所示，图中显示的是德国Voith公司的产品。

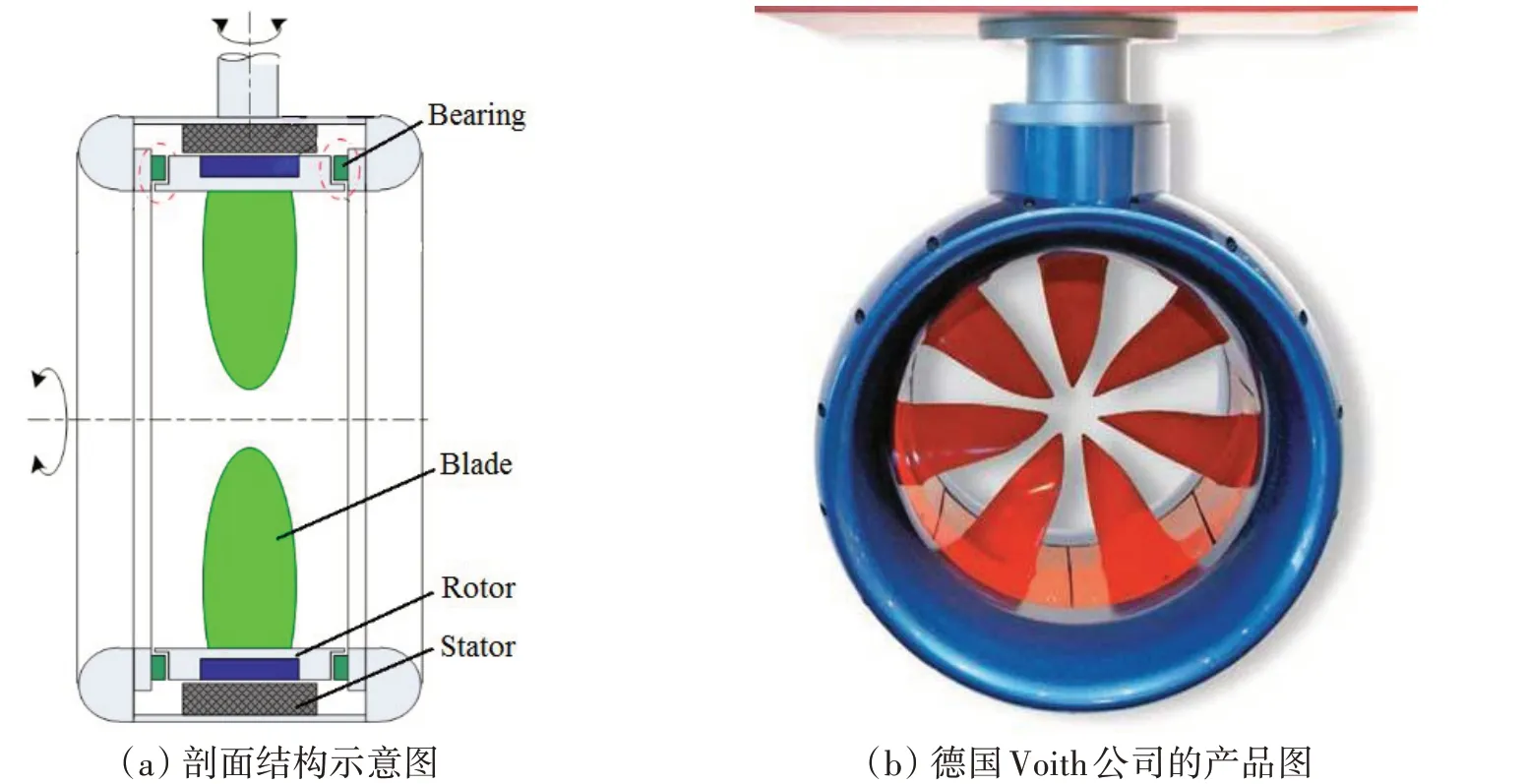
图1 无轴推进器结构及产品Fig.1 Shaftless propeller structure and product diagram

无轴轮缘推进器的理论模型最早出现在1940 年，历经几十年，无轴推进器也从理论模型变为现实模型，并应用于实践，已成为船舶行业里研究的热点。目前针对无轴推进器的电机和水力部件以及轴承的设计研究已得到了国内外研究机构的重视，这些功能模块的性能仿真和优化设计已有文献报道。对于电机的设计，挪威科技大学的Krøvel 等[2]将电机设计理论与有限元相结合，设计了一个100 kW 的永磁电机，满负载实验时温升不超过40℃；海军工程大学胡鹏飞等[3]对1.76 MW 的电机进行了温度仿真，结果显示定子表面的最高温度小于H 级绝缘等级规定的工作温度。螺旋桨作为主要的水动力模型，Yakovlev 等[4]对转速为15 r/s，桨径为0.2 m 的有毂及无毂轮缘驱动推进器进行了仿真分析，得出了无毂RDT 的螺旋桨能获得更高推力和扭矩的结论；武汉理工大学的刘报等[5]针对RDT 间隙流体的摩擦功耗进行了深入的研究，并通过仿真分析与经验公式的对比显示两者吻合良好。水润滑轴承是RDT 的关键部件，设计不当会导致轴承异常磨损和振动，降低RDT 的使用寿命，目前已有学者开展了水润滑轴承结构设计、仿真方法和试验研究[6]。小型RDT 轴承的摩擦功耗较小[7]，在RDT 集成设计中，可适当简化，但大型RDT的轴承摩擦功耗需要重视。

无轴推进器在工作时，处于电磁场、温度场、流体场、应力场等多物理场中，其性能受到多物理场强耦合作用与影响，因此上述功能模块之间存在明显的相互作用关系。为了尽量提高船舶推进力和减少桨叶空化，要求螺旋桨转速较低，例如8 MW 的船舶主机配备的螺旋桨直径超过5.8 m，工作转速约为100 r/min。RDT 驱动电机在桨叶外圈，这就导致电机的直径和重量巨大，例如英国Rolls-Royce的1.6 MW 无轴推进装置内外直径已经分别达到2 m 和2.6 m，干重超过18.3 t。这种水动力设计与电机设计的相互约束关系显著限制了RDT的体积功率密度和质量功率密度的提升。但从国内外研究现状看，目前无轴推进器设计常仅针对电磁场和流场两者之一进行优化设计，这种单因素的设计方法难以实现RDT的综合性能最优化。为此，有必要开展无轴推进器电机与水力部件的集成设计研究。

本文首先从分析无轴推进器的结构特点出发，将电机与螺旋桨之间在结构上存在的约束与联系作为接下来研究电机与水力部件之间协同优化的理论基础；其次介绍电机设计的理论公式以及完成整个设计所需要的约束条件；并基于图谱设计法对导管螺旋桨的几个重要参数进行设计；最后以5.5 kW的推进器为优化算例，对电机与水力部件进行单独优化和耦合优化，并对优化的结果进行分析。

1 无轴轮缘推进器结构分析及优化思路

1.1 结构特点分析

无轴推进器电机与普通电机在结构上有所不同，电机的径向尺寸（指电机内外径）一般都很大，才能足以容纳螺旋桨，这就需要考虑大直径导致的机械性能方面的要求，电机的气隙也要扩大至传统电机的2～3 倍[8]，而轴向尺寸则应相对较小，以保证较高的输出转矩。电机径向厚度（指电机内外径差）要尽可能小以减轻重量。螺旋桨的轮缘厚度和长度是转子高度和长度，螺旋桨的内径加上叶梢间隙就是电机转子的内径，这个叶梢间隙一般取1～2 mm；对于大直径的推进器可忽略，螺旋桨的内径就是转子的内径。当电机充电后，螺旋桨进行旋转，旋转的螺旋桨需要克服旋转阻力，就需要消耗扭矩；在考虑了电机的气隙摩擦扭矩、不考虑其他的机械损失情况下，这个螺旋桨克服的扭矩加上间隙摩擦扭矩可以作为设计电机的输入值，其大小影响电机的性能参数。导管外形要保持良好的流线型，因电机的定子、转子以及轴承都是嵌入到导管中，导管还需要留有足够的空间，但也不能太厚，否则会影响水动力性能；轴承通常安装在轮缘的两端，产生径向强度，起到轴向定位和水冷却的作用，但受导管尺寸的影响，要将轴承设计成体积小、承载能力高、耐磨性好的难度增大。

1.2 耦合优化思路

根据电机和水力部件通过转矩和螺旋桨的直径作为两者联系的介质，建立了电机和水力部件的耦合模型。首先确定设计目标总体效率，并根据各参数之间的联系确定耦合模型的设计参数；其次选择多参数非线性的优化方法；最后给定这些设计参数的初值，设置不等式约束（考虑间隙摩擦扭矩；热模型的导体温度约束；绕组的齿形，永磁体的退磁，电磁转换器电频率；螺旋桨水动力性能参数）和等式约束（电机的尺寸，铜损，铁损，效率；对空泡进行不等式约束；其他约束）条件并进行优化，经过不断地迭代计算得到最优解。具体过程可参阅图2显示的详细步骤。

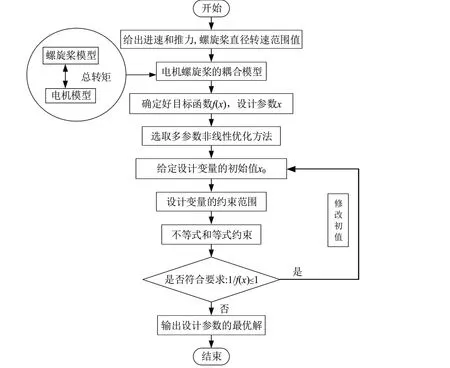
图2 协同优化的流程图Fig.2 Flow chart of collaborative optimization

1.3 多参数、非线性优化方法

对于一些目标函数和约束条件很难用线性函数来表达，且规划问题的目标函数或约束条件有一个以上的非线性时，就需要采用非线性规划。非线性最优化的特点是问题的变量比较多，规模越来越大，问题越来越复杂。本文基于内点法（interior point method）来求解非线性最优化问题。该优化算法需要在可行域内构建一个惩罚函数，在可行域内求惩罚函数的极值点，可通过遍历内部可行区域来搜索最优解；迭代过程始终建立在可行的基础之上，迭代点会循着有效约束边界前进，直到达到问题的最优点[9]。在研究非线性最优化问题方面，可利用有强大优化工具的MATLAB来计算非线性最优化问题，它不仅有进行优化计算的强大优化函数，而且还带有一个非常便于使用的GUI 形式的优化工具，即可根据所要解决问题来选择非线性规划的处理函数。本文提供的设计电机螺旋桨的设计模型，就需要将电机、螺旋桨的一些参数如螺距比（H/DP）、直径（DP）、最佳转速（n）、盘面比（Ae/A0）、电负荷（AL）、电密度（J）、齿形比（kt）、极数（p）、磁体磁极宽度比（β）、填充系数（kf）、磁通密度（B1）等作为设计变量X=(x1,x2,x3,x4,…,x11)，由下面的控制模型可知约束条件是一个非线性问题，其目标函数可设置为：f(x) = 1/(ηelec×ηp)，该目标函数的最小值即为最优解。由此可以说明，该问题是一个多维约束的非线性优化问题。使用MATLAB 中提供的非线性优化的求解函数fmincon，该函数引用了并行机制，可加快梯度计算的速度。其适用于求解最优化问题的形式如下：

式中，X、b、beq和lb为n维列向量，b为m1维列向量，beq为m2维列向量。c(X)和ceq(X)为向量的非线性函数。ub和lb与X同维，为设计变量X的上下界约束。

2 无轴轮缘推进器电机及水力部件的控制方程

2.1 电机的控制模型

无轴轮缘推进器电机设计需要考虑的因素有很多，该永磁电机内部结构如图3所示（其中参数含义将在下文给出），包括安装在导管中的定子、与桨叶连接的转子，以及将定子和转子与水隔离的护套。其中，与普通永磁电机的重要不同在于定/转子间隙有水流过以冷却电机和润滑轴承，因此电机流场也是关键因素。围绕电机的性能，本文拟建立的模型将电磁场、温度场和流场等因素考虑在内，通过调整设计变量来优化设计目标效率，确定这些设计参数为AL、J、p、β、B1、kf、kt的约束条件，可以得到唯一解[10]。

图3 无轴轮缘推进器电机的结构Fig.3 Structure of RDT’s motor

电机由电磁感应转换给转子的转矩为电磁转矩（TEM），其表达式为

式中，TEM为电磁转矩，kb1为绕组系数，AL为电负荷，B1为磁通密度，D为间隙直径，L为铁芯轴向长度，ψ为定子电流与转子感应电动势之间的角度。

考虑到径向间隙和轴向间隙摩擦转矩[11]，径向间隙的摩擦转矩，采用由经验得出的BelGand 和Boulos模型[12]。该经验模型的径向间隙雷诺数ReT=ρΩRhG/μ，适用于本实验的经验公式的表达式为

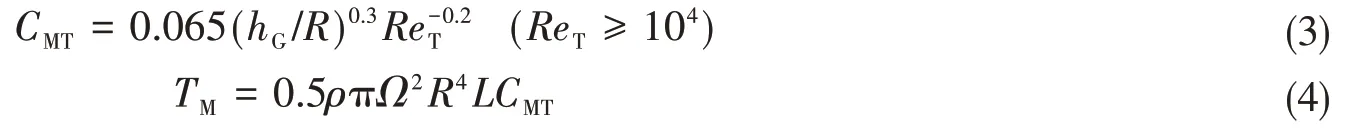
式中，hG为径向间隙高度，ρ为流体密度，Ω为旋转角度，μ为流体的运动粘度，L为轮缘长度，R为转子外径，TM为轴向间隙摩擦转矩。

轴向间隙选用Daily 和Nece 提出的经验模型[13]。下标1，2 分别表示轮缘前后端面，其轮缘端面的摩擦扭矩的表达式为

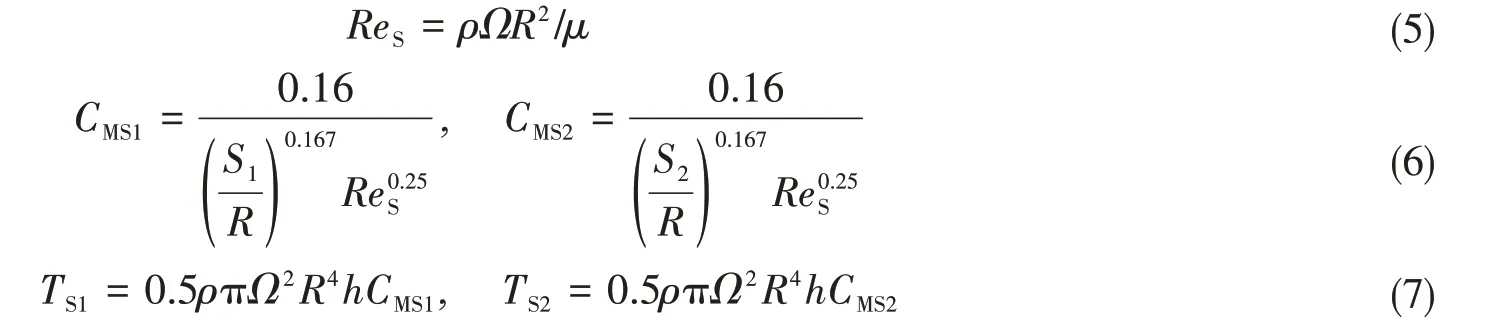
式中，S为轴向间隙宽度，h为轮缘高度，ReS为轴向间隙雷诺数，TS为径向间隙摩擦转矩。

气隙高度（hG）是很关键的影响因素，其大小直接影响电机的性能，其表达式为

式中，kG为考虑多物理场影响的间隙因素系数，k为考虑直径大小影响的间隙因素系数。

在有径向磁通的情况下，磁体高度（hM）与间隙磁通密度（B1）的表达式为

式中，β为磁体磁极宽度比，Br为永磁体剩磁，μr为永磁体相对磁导率。

考虑到开槽效应，其影响系数ks为

磁阻Re为

式中，kt为齿形比，h'M为磁高，ws为槽高，Spp为每极每相的槽数，m为相数。公式（12）、（13）适用于薄气隙的情况，公式（14）适用于厚气隙的情况。

槽高（hS）和齿高（hT）相等，其表达式如下：

通常选择转子和定子磁轭的最小高度hY(min)作为设计值，其表达式为

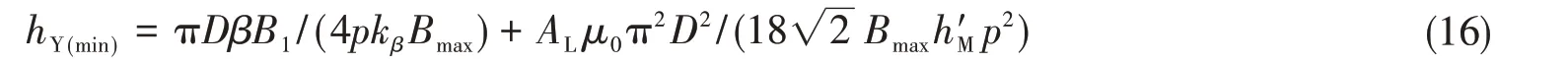
该公式适用于存在径向经向磁通，且每极每相一槽的三相绕组情况。间隙直径D的表达式为

式中，hH为定子、转子附加厚度，Dint为转子的内径。

铁损可根据硅钢片供应商提供的经验数据进行计算，定子磁路中每单位质量损耗总损失pFe的表达式为

式中：f为铁中的电频率；BFe为铁中的磁通密度；pFe0为在给定频率f0和磁通密度BFe0单位质量的铁损耗，这里b=1.5，c=2.2。假定定子各处的磁通密度为Bmin，可得总损耗pFe。

假设铁损主要是由转子的旋转引起，则电磁转矩TEM的表达式为

式中，TMeca为机械转矩。考虑了水动力摩擦转矩忽略其他机械损耗的情况下，螺旋桨输出转矩（Q）与间隙摩擦扭矩的和作为输入数据，即TMeca=Q+TS1+TS2+TM。

电流和每相绕组电阻以及铜损的表达式如下：

式中，ns为每相每极绕组匝数，Scond为导体截面，Lcond为绕组导体总长度，ρ1为导体电阻率。

电效率表达式为

另外考虑了一些不等式约束：物理因素方面有永磁体和绕组的齿饱和度问题、退磁、齿和磁体的完整性、永磁体的尺寸约束等，温度方面有导体的极限温度的限制，以及电的特性方面包括电频率以及时间常数等。

在ψ=0，Spp=1，m=3的情况下，考虑磁铁的齿饱和度和绕组的齿饱和度需满足的表达式：

齿形需满足准则的表达式：

式中，wT为齿宽，Rmax为齿形完整性的极限比。

磁体高度与宽度的比满足表达式：

磁体退磁的约束表达式为

永磁体一般采用稀土永磁材料，如钕铁硼或钐钴。因钐钴的耐受温度高于钕铁硼，选择的永磁体材料是Smco30M，其矫顽力Hcj=1 000 kA/m。

参见文献[14]中的热模型，导体最高温度TCu(max)约束的表达式为

式中，Tmax为导体极限温度，与导体材料有关。

因电机是嵌入到导管中的，电机的厚度hEM（包括端部绕组）必须低于导管厚度hduct，电机Lmach的总长度小于导管长度Lduct，导管厚度hduct、导管长度Lduct与螺旋桨直径成线性关系，即hduct=khductDP，Lduct=kLductDP，且kLduct<1，khduct<1，约束表达式为

电压转换器的电频率需满足实际值、电机的电频率和电机的时间常数的约束，其表达式为

式中，Lmach为同步电机电感（包括槽漏电感），可见文献[15-16]中的同步电感经典方程。

2.2 水力部件的控制模型

螺旋桨的设计方法大致可分为两种[17]：理论设计法和图谱设计法。因理论设计法设计制造比较复杂，所以直接利用基于图谱法导管螺旋桨敞水实验的回归方程进行设计，利用Ka 系列导管螺旋桨敞水实验的回归方程对导管螺旋桨进行设计。

在导管螺旋桨的设计过程中,找到各个参数的约束条件是设计最优桨的关键。已知进水速度V与要求的推力T，在螺旋桨的优化设计中，涉及的参数有很多，主要有螺旋桨的螺距比（H/DP）、直径（DP）、最佳转速（n）、盘面比（Ae/A0）等。文中将以上参数作为水力部件的设计变量,将效率作为目标进行优化设计。其中水力部件的效率的表达式为

式中，进速系数J0=V0/(nDP)，推力系数KT=T/(ρWn2)，转矩系数KQ=Q/(ρWn2)。

推力系数（KT）和转矩系数（KQ）可按Ka系列导管螺旋桨试验资料的回归公式[18]计算：

采用Keller公式[19]，不发生空泡条件约束的表达式为

式中，p0是螺旋桨中心的静压力，pV是15℃下的水的汽化压力，K为补偿系数，T为推力。

考虑汽蚀风险，限制最大叶片尖端速度的表达式为

其他约束条件有：0.5 ≤H/DP≤1.4；0.3 ≤Ae/A0≤1.05；0.25 ≤DP≤0.4；900 ≤n≤1100。

3 仿真结果及分析

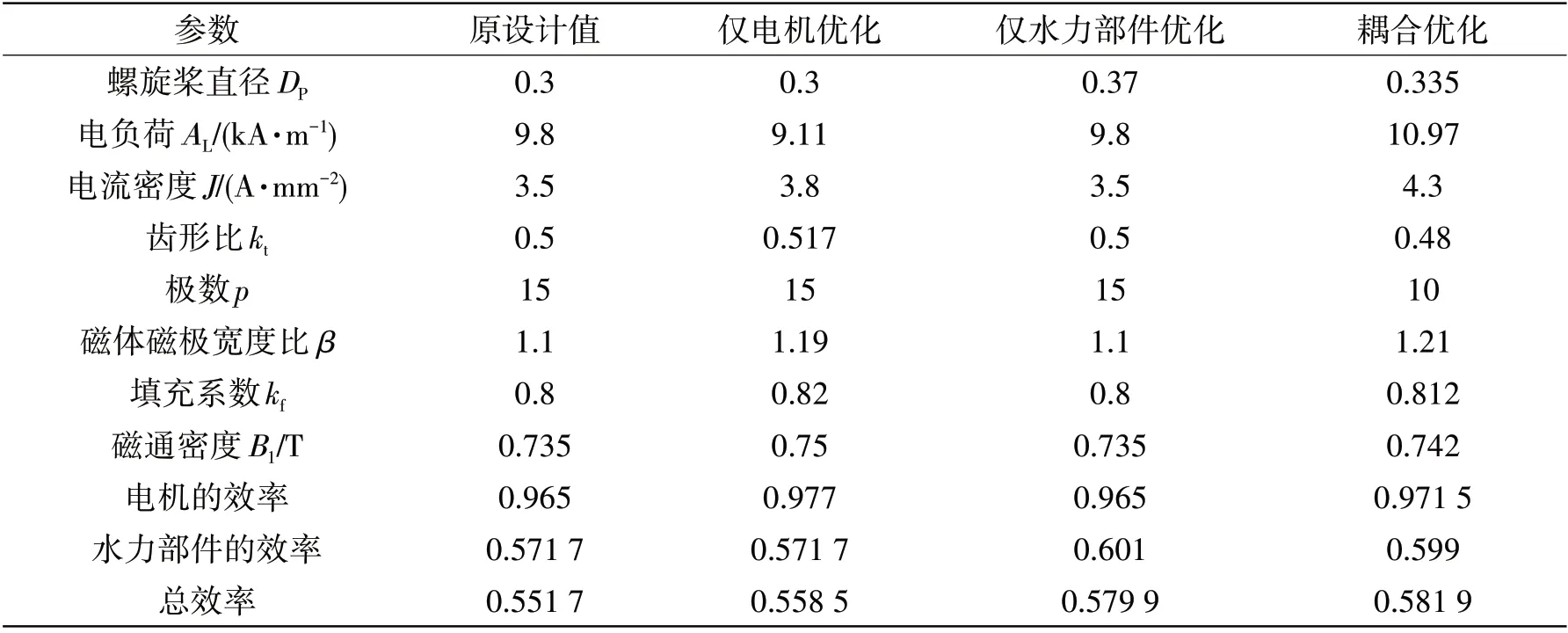
由于电机的设计公式之间都是相互联系的，可以进行公式的缩减，简化约束条件。选用5.5 kW的推进器进行优化设计，在进速V=1.8 m/s，要求的推力为T=1 500 N 的情况下，选用的螺旋桨为JD7704+Ka4-70，根据该螺旋桨的敞水特征曲线的回归系数，对推进器的推力系数和转矩系数进行计算，原设计螺旋桨的参数为n=1 000 r/min，Dp=0.3 m，盘面比Ae/A0=1.2，螺距比H/DP=0.7，效率为0.571 7。先对水力部件进行独立优化，采用多参数非线性优化方法得出水力部件的优化参数以及效率；根据优化出导管桨的直径和转矩作为电机的输入值，对电机的设计参数进行优化得出电机的优化结果；最后将电机与水力部件的约束放在一起，以转矩和直径作为约束之间的联系，从而得到对两者的耦合优化，采用相同的优化方法，以总的效率作为目标函数对该耦合模型进行迭代优化，得出优化参数值以及总效率值，再计算得出电机与水力部件的效率值。通过与单独优化的值进行对比，验证了该方法的合理性。单独优化与耦合优化的结果见表1。

表1 优化的结果Tab.1 Results of optimization

续表1

从电机和螺旋桨的单独优化的结果可以看出，电机与水力部件单独优化的总效率分别是0.558 5和0.579 9，较原设计的总效率高，说明该优化方法有一定的优势。将两者进行耦合优化后的结果与单独优化的结果进行对比后发现，单独优化与耦合优化后螺旋桨的直径、电负荷、电流密度以及磁通密度的值等参数值的变化相对来说比较明显。耦合优化后的螺旋桨的直径降低了，其可能的原因是受电机尺寸的影响；电机的电负荷增加会导致电流的增加，从而增加电机的铜损耗，另外也会减少电机的尺寸，电流密度增加也会减少电机的尺寸；电机的磁通密度相对于单独优化略微降低，但相对于优化之前的值是增大的，其值增大会使电机铁心的尺寸略微减少，铁损增加。综合结果可知，耦合优化的电机的效率略低于仅电机单独优化的效率，耦合优化的水力部件的效率略低于仅水力部件单独优化的效率，但耦合优化的总效率0.581 9却高于仅电机单独优化的总效率0.579 9和仅水力部件单独优化的总效率0.558 5，说明耦合优化对整体效率的提高有一定的优势，耦合优化可以综合两者之间的制约关系使整体的优化达到最佳值。另外该模型使用的是一阶公式，相对于一些微分、积分方程计算快，缩短了优化设计的时间。

4 结 论

（1）无轴轮缘推进器的设计涉及到很多学科如电磁学、热力学、流体力学等，各学科之间存在很强的制约与联系，分析其中的一两个设计因素难以实现无轴推进器的综合性能最优化。

（2）由于无轴推进器的气隙尺寸相对于普通电机的大，水流过气隙时的摩擦扭矩就会相应地增加，因此将无轴推进器的轴向和径向间隙流动的摩擦扭矩作为优化设计的考虑因素。

（3）根据电机和主要的水力部件之间存在的内在联系，建立电机和水力部件的控制模型，该模型选用的是一阶分析数学模型，减少了计算的复杂性，缩短了设计时间，具有一定的精度。

（4）选用5.5 kW无轴推进器进行设计，采用多参数非线性优化方法对推进器件进行单独优化和协同优化，并与原始数据进行对比。结果显示，耦合优化推进器的总体效率提高了5.5%，使效率高达0.581 9，但耦合优化的电机的效率和水力部件的效率都低于仅电机单独优化的电机效率或仅水力部件单独优化水力部件的效率，这也体现了电机与水力部件相互制约的关系，也说明了耦合优化的重要性。