基于衍射光栅的高精度干涉星敏感器的理论分析
2021-11-25张淑芬王建立李文昊
张淑芬,姜 珊,董 磊,王建立,吴 娜,李文昊*
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)
1 引言
星敏感器以除太阳外的恒星为观测对象,利用星体在星敏感器上所成的像获得星体在星敏感器坐标系中的单位矢量,并通过计算星体在星敏感器坐标系中单位矢量相对于星体在天体坐标系中单位矢量的坐标变换矩阵,得到载体飞行姿态[1-3]。其输出的姿态测量精度可以达到角秒级甚至亚角秒级,并且具有无时间累积误差、能够自主导航的优势,已经成为目前测量精度最高的姿态敏感器[4-10],在地球遥感、地球测绘、洲际导弹和行星测绘等方面得到了广泛应用。随着航空航天事业的飞速发展以及应用场合的特殊化,高精度、大视场、轻小化已经成为星敏感器的发展趋势[11]。
星敏感器测量精度包括单星测量精度和姿态测量精度。提高姿态测量精度是提高星敏感器测量精度的最终目的,提高单星测量精度是提高星敏感器姿态测量精度最本质的方法。星敏感器单星测量精度与星点质心提取精度、探测器像元阵列数及视场有关[12-14]。提高星点质心提取精度常采用离焦的方式,令恒星在星敏感器上的像点弥散在几个像元内,通过内插细分定位算法使星点质心提取精度达到亚像元甚至更高[15-16]。在像点内插细分定位算法中,多忽略像差的影响,利用高斯分布模型表示星像点能量分布[17-18]。虽然已有研究表明该模型合理,但是光学像差会引起弥散斑分布的改变从而降低星点质心提取精度[19],不适于在甚高精度星敏感器上的应用。提高探测器像元阵列数,可以提高单星测量精度,但提升幅度有限,并且会带来额外花费。在探测器确定的情况下,通过增大光学系统焦距的方法缩小星敏感器视场,可以提高单星测量精度。但是光学系统焦距的加大,会使星敏感器体积变大,不利于在微小卫星等航天器上的应用;另外,视场的缩小减少了视场内导航星数目,使星敏感器探测能力降低,不利于星图识别和星敏感器动态范围的提高。在焦距确定的情况下,增大光学系统相对孔径可以提高星敏感器探测到暗星的概率,从而提高星敏感器的探测能力[20-23]。但是在焦距不变的情况下,光学系统相对孔径的增大不仅会增加星敏感器的体积和质量,还会增大光学系统像差,影响星点质心提取精度。此外,视场内探测到暗星的概率增加,会使星表尺寸变大,星图识别算法变得更加复杂,姿态更新速率降低。美国洛克希德马丁先进技术中心设计的AST-301是目前已知星敏感器中输出姿态测量精度最高的产品,两组AST-301配合使用时,姿态测量精度达到0.18″,但是星敏感器总质量达到了14.2 kg,视场仅为5°。由于视场较小,为保证星图识别的准确率,其极限探测星等为8.5等星,造成导航星数目庞大,姿态更新速率仅为2 Hz。传统星敏感器的测量精度受视场、体积、质量和姿态更新速率等性能的制约。
由于星敏感器精度与视场、体积、质量等性能难以兼顾,传统微型星敏感器的测量精度普遍较低,其精度等级较大型星敏感器相差近一个量级。典型的微型星敏感器主要有[24-25]:莫斯科罗蒙诺索夫国立大学斯特恩伯格研究所设计的STC-2星敏感器、德国维尔茨堡大学设计的Picostar星敏感器、加拿大瑞尔森大学设计的ST-16星敏感器。STC-2星敏感器是目前已知质量最轻的星敏感器,不计遮光罩仅重65 g,视场19.64°,功耗仅为250 mW,但是其姿态测量精度只有10″;Picostar星敏感器质量仅有70 g(不计遮光罩),体积仅为30 mm×38 mm×80 mm,视场为12.51°,但是由于其图像传感器分辨率较低,姿态测量精度仅为36″;ST-16星敏感器在轻小型星敏感器中姿态测量精度相对较高,x/y轴姿态测量精度达到了7″,视场20.03°,但是其姿态更新率仅为2Hz。
为克服传统星敏感器的缺陷,美国Optical Physics公司(OPC)率先开展了干涉星敏感器的研究,在视场为20°,光学系统仅重200 g的情况下,单星测量精度理论上可达0.11″[26],从原理上打破了传统星敏感器精度与视场、体积、质量等性能间的相互制约。浙江大学的杜鹃等人在此基础上提出了一种基于二维光栅的双轴干涉星敏感器装置,其单星测量角分辨率达0.2″[27-28]。该装置可以同时提高x、y方向星光入射角度的测量精度,但是该装置由于用到双光栅衍射级次的+1级或−1级,使得宽波段的星光在衍射方向会存在严重色散;另外从x、y方向分别对入射光强细分,使探测器上像点光强信号进一步减弱,增加了探测难度,其实用性有待提高。为深入研究基于光栅干涉测量原理的星敏感器,打破西方国家对我国的技术封锁,本文研究了一种基于一维衍射光栅的高精度干涉星敏感器结构,对星光场在干涉星敏感器中的光学传输过程进行数学建模,得到干涉星敏感器上像点质心位置、像点能量与星光入射角度之间的关系,确定了利用星体在干涉星敏感器上像点的质心位置和相对能量分别进行粗定位和精定位的方法及粗精定位结合的方法,通过公式推导得到了干涉星敏感器单星测量角分辨率的影响因素,并通过模拟仿真验证了干涉星敏感器精定位和粗精定位结合的可行性。
2 基于光栅干涉测量的星敏感器基本原理
基于一维光栅的干涉星敏感器光学元件部分如图1所示,主要由光学干涉部分、角度调制部分和光学成像部分等3部分组成。光学干涉部分使经过的星光发生干涉,角度调制部分对入射星光产生不同方向的偏转,光学成像部分将不同方向的光成像至探测器的不同位置。其中光学干涉部分由两块周期相同、刻线方向间有一微小夹角ε且距离为d的光栅G1、光栅G2组成,角度调制部分由4块光楔组成,光学成像部分与传统星敏感器相似,由成像透镜组组成。光学干涉部分和角度调制部分是干涉星敏感器精定位的关键,也是与传统星敏感器的区别之处。
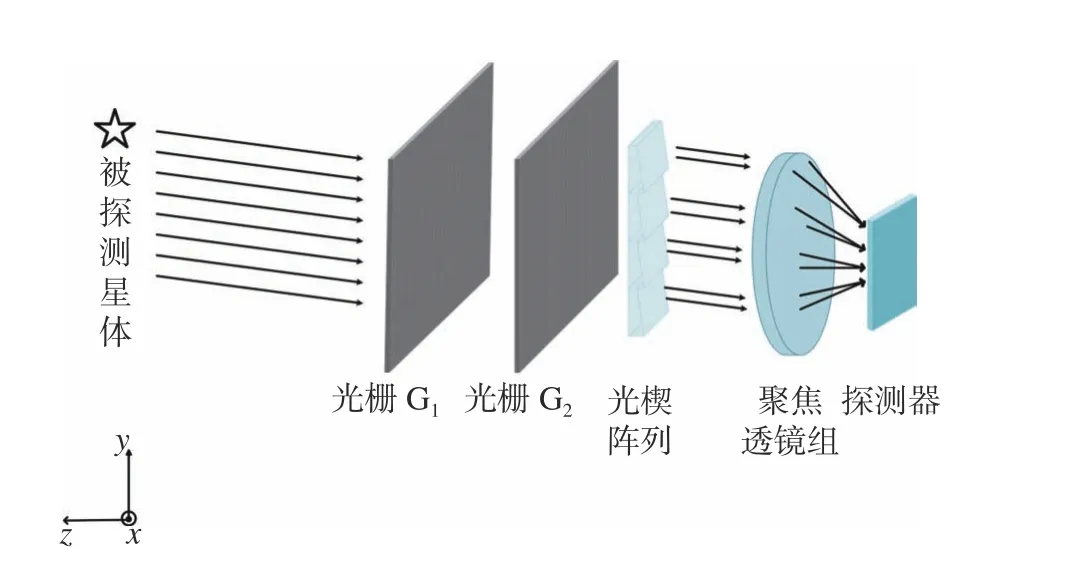
图1 基于一维光栅的干涉星敏感器光学系统结构图Fig.1 Configuration of interferometric star tracker optical system based on 1-D grating
为方便分析星光场在干涉星敏感器中的传输过程,得到探测器上像点与星光入射角度之间的准确关系,建立了如图2所示的干涉星敏感器靶面坐标系x'O'y'和干涉星敏感器坐标系O-xyz。在x'O'y'中,O'为探测器的几何中心,x'轴、y'轴分别与探测器阵列的行、列平行。在O-xyz中,以主点O(沿光轴距离靶面坐标系为F的点,F为星敏感器光学系统的焦距)为坐标原点,光轴指向为z轴正方向,与探测器像元阵列行、列平行的坐标轴分别为x轴、y轴,并且干涉星敏感器坐标系符合右手准则。P点代表星像点。

图2 干涉星敏感器靶面坐标系x'O'y'和干涉星敏感器坐标系O-xyz间的关系Fig.2 Relationship of target plane coordinate system x'O'y'and the coordinate system O-xyz of the interferometric star tracker
图1中光栅G1的刻线方向与y轴平行,光栅G2的刻线方向与y轴有一微小夹角ε,两块光栅周期均为p,并且两块光栅间距为d。光楔阵列在平行于xOy面的平面上沿y轴方向摆放,光楔在x方向上的长度为a,y方向上的长度为b。
单颗星发出的平面光波场在任一选定的平行于xOy面的平面上可表示为

式中:A为实数,代表光波场振幅;λ代表星光发出的任一平面波的波长;θx和θy分别为平面光波与干涉星敏感器坐标系x轴、y轴夹角的余角。
应用角谱理论[29],当入射星光经过光栅G1后发生衍射,其衍射光场分布的空间频谱等于入射光场频谱与光栅G1频谱的卷积,即

式中Fi(fx,fy)为星光光场的频谱,即平面光波场Ui(x,y)的傅立叶变换,G1(fx,fy)表示光栅G1的频谱。
入射至光栅G2之前,由于光会在均匀介质或空气中传播一段距离d,虽然振幅不受影响,但会引入与频率有关的相移。此时,场分布的空间频谱为

式中H(fx,fy)表示传递函数。
在经过光栅G2后,各级衍射光发生干涉,干涉光场分布的空间频谱变为

式中G2(fx,fy)表示光栅G2的频谱。
经过光楔阵列后,光场分布的空间频谱为
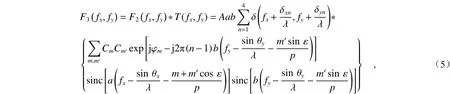
式中T(fx,fy)为光楔阵列的频谱,即光楔阵列透过率函数的傅立叶变换;n代表光楔阵列中第n块光楔,n=1,2,3,4;a和b分别代表光楔在x轴方向上的长度和在y轴方向上的长度;m和m'分别表示光栅G1的m级衍射和光栅G2的m'级衍射;Cm和Cm'分别表示光栅G1的m级衍射系数和光栅G2的m'级衍射系数;φm代表经过光栅G1衍射后的m级衍射光在入射至光栅G2之前,传播距离d后引入的相移,表示为
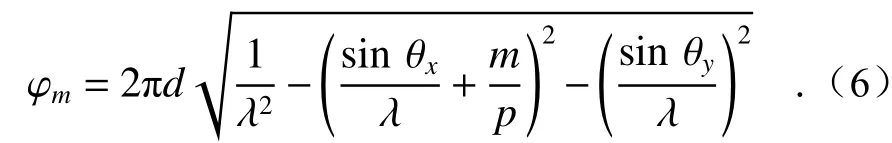
根据透镜组傅立叶变换的性质[29],透镜组后焦面(x'O'y'平面)上的光场分布UF(x',y')正比于前方物体的频谱,并使物体产生一个位相弯曲,星光经过成像透镜组后,在透镜组后焦面上的光场分布为:

式中F表示透镜组焦距,d0表示光楔阵列到成像透镜组中第一块透镜的距离。
2.1 粗定位
由于光楔阵列由4块不同楔角的光楔组成,所以同一方向的入射光经过光楔阵列后会偏转成为4束不同方向的光。又因为不同方向的光经过成像透镜后会成像在后焦面的不同位置,所以入射星光经过光楔阵列后会在干涉星敏感器上形成4个像点。为方便讨论,假设光栅G1和光栅G2只有0级和±1级衍射,即m=0,±1;m'=0,±1。由于非零级衍射级次存在色散,影响像点质心定位,故仅考虑0级,即(0,0),(+1, −1)和(−1, +1)级衍射光干涉后的频谱,则经过第n块光楔偏转后的星光,在透镜组后焦面上像点的光强分布为

式中UF,n(x',y')表示星光经过第n块光楔偏转后在后焦面上的光场分布。
设面阵探测器第(i,j)像元的中心坐标为,以像元尺寸(pixel)为单位,则星光经过第n块光楔偏转后形成的像点在该像元内的能量为
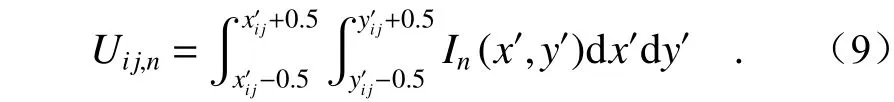
采用灰度加权质心法,得到星光经过第n块光楔偏转后在探测器上像点的质心坐标(xn',yn'),即

由式(8)像点光强分布,根据sinc函数的性质,得出像点质心坐标(xn',yn')与光楔偏转角(δxn,δyn)的关系为

由式(11)可以看出,光楔引入的角度偏移在透镜后焦面上表现为星体像点位置的平移。所以在不设置光楔阵列的情况下,目标星在干涉星敏感器上的像点坐标(X0,Y0)为
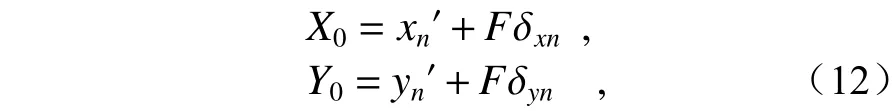
并且
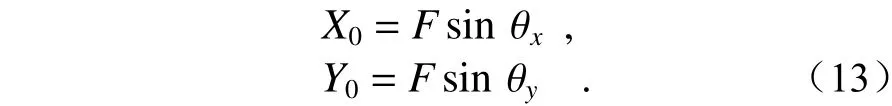
因此,可以通过探测器上像点的质心坐标(xn',yn')与光楔偏转角(δxn,δyn)之间的关系,得到不设置光楔阵列情况下目标星的像点坐标(X0,Y0),从而获得星光入射角度,进行粗定位。
由式(8)像点光强分布的相位项可以看出,像点光强分布与星光入射角度有关,因此星光入射角度变化过程中,存在使某像点光强分布In(x',y')为零的情况,这会导致该像点质心坐标(xn',yn')无法被提取到。为有效获取像面上的星点坐标(X0,Y0),对瞬时状态下提取到的像点质心坐标(xn',yn')进行加权运算,即

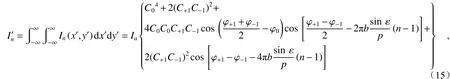
式中Ia=(Aab/λF)2。
2.2 精定位
由于式(15)像点光强的相位项中包含了与星光入射角度有关的信息,因此可以通过单个星体在探测器上所成4个像点的相对光强得到像点光强的相位信息,进而获得星光入射角度θx。
根据式(6),有

记φ=φ+1−φ−1。由式(16)可以看出,像点光强中包含的项与波长有关,会干扰φ的计算,所以抑制光栅零级衍射,即C0=0。
令光楔沿y轴的长度代入式(15)并整理,得到4个像点的光强分别为

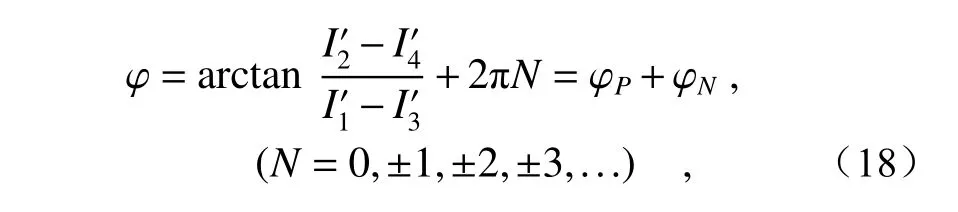
通过星点提取各像点能量可以得到φP, 作为干涉星敏感器的精定位信息。
2.3 粗精结合
将式(13)中第一个式子与式(16)中第二个式子联立,可得
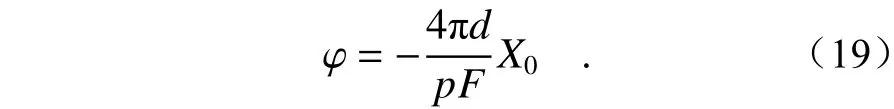
由于质心提取坐标精度受视场、探测器像元数和焦距等参数限制,因此将求取得到的质心坐标(X0,Y0)代入式(19),得到

式(20)中的中括号表示对该括号内的数取整,所以利用星光不经过光楔发生偏转时的像点坐标(X0,Y0)即可得到φN。
由以上分析可以看出,单个星体在干涉星敏感器上形成4个像点,通过星点提取得到各像点质心坐标及能量。对提取到的像点质心坐标进行加权运算,得到在不设置光楔阵列情况下,目标星体在星敏感器上的像点坐标(X0,Y0)。利用坐标(X0,Y0)进行粗定位,利用4个像点的相对能量进行精定位,并将粗定位与精定位结合,获得星光入射角度θx。
在实际计算过程中,通过传统的质心求取方法获得的质心坐标作为星光入射角度的粗定位,其精度与视场、图像面阵大小相关。对于进一步进行细分的光强变化,由于其呈周期性变化,为保证角度测量的唯一性,因此由质心提取计算的角度精度应不低于光强信号变化周期对应的角度。探测器上像点光强变化一个周期对应的角度为Δθx,有[sin(θx+∆θx)−sinθx]=2π,则

因此星点质心提取得到的X0的精度ΔX0应不低于,即ΔX0≤。由于星点质心坐标X0的计算精度与视场和探测器阵列数有关,因此在系统设计时会根据视场和探测器阵列参数,合理选择光栅周期p、两块光栅之间的距离d。
像点光强信号每变化一个周期采用M倍电子学细分,则单星测量角分辨率σ可表示为
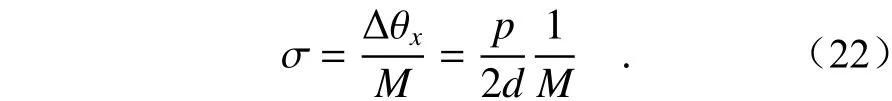
由式(22)可看出,单星测量角分辨率与光栅周期p、两块光栅之间的距离d及像点信号的电子学细分倍数M有关。基于光栅的星敏感器在传统星敏感器求取质心的基础上,利用星点的光强信息进一步进行细分,因此突破了质心求取的精度限制,在相同的视场和探测器阵列数下可以获得更高的角度测量精度。对于视场为20°×20°,焦距为40 mm、探测器像元阵列数为1000×1000,光栅周期为50 μm,两块光栅距离为50 mm的干涉星敏感器,当电子学细分采用1024倍细分时,经计算得到单星测量角分辨率为0.1″。
典型传统星敏感器的像点质心细分算法精度一 般 为1/10~1/50 pixel。对 于 视 场 为20°×20°,焦距为40 mm、探测器像元阵列数为1000×1000的传统星敏感器,其单星测量角分辨率最高仅为1.44″。对于视场、焦距、探测器像元阵列数与传统星敏感器相同的干涉星敏感器,当质心细分算法的精度为1 pixel,光栅周期为50 μm,两块光栅距离为50 mm,并且电子学细分采用1024倍细分时,其单星测量角分辨率可达0.1″,与传统星敏感器相比,虽然重量稍有增加,但是单星测量角分辨率提高了一个数量级。传统星敏感器若要达到与干涉星敏感器相同的单星测量角分辨率,则需要通过增大焦距的方法,将其视场至少缩小为原来视场的1/14.4,与干涉星敏感器相比,传统星敏感器体积增加了5倍以上。
基于光栅的干涉星敏感器要求光栅±1级衍射效率最高,同时抑制0级及其他衍射级次,并且在工作波段内光栅及两块光栅间隔层材料的色散特性尽量小。因此在进行干涉星敏感器设计时,应根据探测需求,从系统整体性能出发,选择合适的光栅结构和光栅周期,抑制无贡献衍射级次,降低色散,以提高系统光能利用率、信噪比及测量精度。
3 计算机仿真
前面介绍了干涉星敏感器光学系统基本元件,并对星光在干涉星敏感器光学系统中的传输过程进行了数学建模,得到了粗精定位结合的基本原理。为验证精定位及粗精定位结合的可行性,本部分对视场内星光入射角θx变化引起的探测器阵列上像点光强的变化及φ与星光入射角θx之间的关系进行模拟仿真。
3.1 仿真参数
初始条件和基本参数为:(1)朗奇光栅偶数级次衍射为零,可以使零级衍射C0得到抑制。因此采用朗奇相位光栅,并且光栅周期为50 μm,两块光栅距离为50 mm,两块光栅间的刻线夹角为0.057°。(2)楔形棱镜尺寸均为12.5 mm×6.25 mm。(3)透镜组焦距为40 mm。(4)模拟的光谱范围为550~630 nm,取样波长间隔为10 nm。
3.2 仿真结果
视场内3颗恒星在干涉星敏感器上的成像情况如图3所示。由图3可以看出,每一颗星在干涉星敏感器上均成像为4个像点,并且这4个像点组成一个方形区域。由于4块光楔在不同方向上的偏转角度相同,因此方形区域的中心即为恒星光经过光楔不发生偏转时在干涉星敏感器上所成像点的位置。由于4个像点之间的距离与焦距F和光楔偏转角度(δxn,δyn)有关,因此在进行干涉星敏感器设计时,为避免像点重叠影响星点提取,应合理设置透镜组焦距和光楔楔角。

图3 视场内3颗星在干涉星敏感器上的成像Fig.3 Star pattern generated for three stars within the field of view
为验证干涉星敏感器精定位的可行性,仿真模拟该视场内任一颗恒星,在干涉星敏感器上所成4个像点的光强随星光入射角θx的变化曲线,如图4所示。图4表明:4个像点的光强均随星光入射角θx的变化呈正弦规律变化;在不同入射角度下,4个像点的总能量不变。因此可以根据干涉星敏感器光学元件及特点,由光学传递函数推导像点光强的相位与星光入射角的关系,并由4个像点的相对光强得到φP,从而对载体进行精定位。

图4 像点光强随星光入射角θx变化曲线Fig.4 Intensity of four spots changing with the incident angle θx
为验证干涉星敏感器粗精定位结合的可行性,模拟了在全视场2ω=40°(−20°≤θx≤20°)情况下及在小角度入射(0≤θx≤1 mrad)下φ与星光入射角θx之间的关系曲线,分别如图5和图6所示。图5和图6均表明:φ与星光入射角度θx之间存在线性关系。因此可以将粗定位与精定位相结合求得φ,从而通过φ与星光入射角度θx之间的关系获得θx。
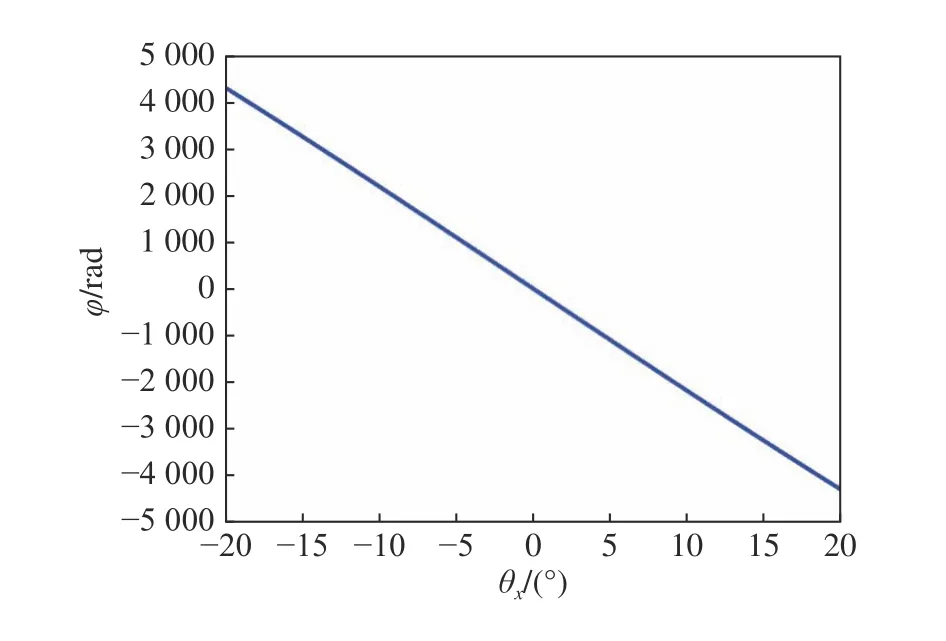
图5 φ随星光入射角θx的变化Fig.5 φ changing with the incident angle θx

图6 小角度下φ随星光入射角θx的变化Fig.6 φ changing with the small incident angle θx
在特定角度(θx=0, 0.125, 0.250, 0.375, 0.5 mrad)下,该星体在探测器上像点的图案如图7所示。图7表明:最亮像点的位置在4个像点中交替变化;在特定角度下只能看到3个星像点。这是因为像点光强随着星光入射角度变化而呈正弦规律变化,并且在某些特定角度下,第4个像点光强为零。

图7 单个星体在探测器上的星图Fig.7 Star pattern from one star on the detector
图4和图7均表明,星光入射角度每变化 0.5 mrad,像点的光强变化一个周期。因此像点光强信号每变化一个周期采用1024倍电子学细分的情况下,计算得到单星测量角分辨率为0.1″。
4 结论
测量精度的不断提高是星敏感器发展的不变方向。单星测量精度是评价星敏感器测量精度的基本指标,也是提高星敏感器测量精度的最本质方法。本文提出的基于光栅的干涉星敏感器,其单星测量角分辨率与光栅周期、两块光栅之间的距离及像点信号的电子学细分倍数有关。由于在传统星敏感器求取质心的基础上,利用星点的光强信息进一步进行细分,因此突破了质心求取的精度限制,在相同的视场和探测器阵列数下可以获得更高的角度测量精度。仿真模拟得到的干涉星敏感器单星测量角分辨率可达0.1″,与传统星敏感器相比,其单星测量角分辨率提高了一个数量级。本文的工作为深入开展基于衍射光栅的高精度干涉星敏感研究及我国实现自主研发新一代高精度轻小型星敏感器奠定了基础。
