大气气溶胶消光后向散射比反演方法研究
2021-11-25童奕澄
陈 洁,童奕澄,肖 达,张 凯,刘 崇,刘 东
(浙江大学 光电科学与工程学院 现代光学仪器国家重点实验室,浙江 杭州 310027)
1 引言
气溶胶是大气成分中的三大活跃成分之一,对气候变化及空气质量具有重要影响,研究气溶胶粒子的光散射特性是大气探测中一个重要课题[1]。早在1953年学者们就开始通过实验和理论研究粒子消光系数和后向散射系数之间的关系,且发现两者的比值——消光后向散射比(Extincion-to-Backscatter Ratio, EBR)只和颗粒物的组分及相对尺度谱分布有关[2]。而美国国家大气研究中心的Blifford(1969)等人通过机载原位仪器实测发现,气溶胶层内粒子的相对尺度谱分布基本不随高度变化,可以假设同一层气溶胶的EBR值恒定[3]。之后美国亚利桑那大学的Fernald(1984)在EBR值恒定且已知的假设下,推导了米散射激光雷达反演气溶胶光学特性参数的形式解,即目前广泛应用的Fernald法[3]。在Fernald法中,EBR值的误差对消光系数等其他参数的反演有非常重要的影响,且在实际复杂的大气状况下,假设EBR值恒定也是误差的重要来源[4]。此外,EBR值还可用于区分不同类型气溶胶[5]。因此,实现气溶胶EBR的高精度反演对大气科学研究具有重要的意义。
本文对各类气溶胶EBR的反演方法进行了整理归纳,并重点介绍了其中较为主流的光散射模型法、被动光学遥感法及激光雷达法,分析了各自的适用情况及优缺点,可为相关领域研究者提供参考。
2 气溶胶EBR反演方法概述
反演大气气溶胶EBR的方法可归纳为图1所示的框图。根据使用的仪器及反演原理,可分为光散射模型法、被动光学遥感法、激光雷达法、积分浊度计测量法、多项式函数拟合法等,但本质上都是从气溶胶的微物理特性或光学特性入手来进行反演。

图1 各类气溶胶EBR反演法之间的联系框图Fig.1 Block diagram of relationship between various aerosol EBR inversion methods
由于气溶胶的光学特性是其微物理特性在光散射作用下的一个映射集,而光散射理论根据电磁学推导了该映射的函数关系,故光散射模型法可根据已知的气溶胶微物理特性计算相应的EBR,其反演精度取决于微物理特性的准确度及采用的算法。
气溶胶的微物理特性与湿度等环境因素紧密相关,尤其对于吸湿性气溶胶来说,吸湿增长将导致其粒径与复折射率发生显著变化[6]。德国科学家Ackermann(1998)等结合米散射理论和气溶胶吸湿增长模型,模拟了大陆、海洋以及沙尘气溶胶在8种不同湿度下的光学特性,并据此拟合出了能计算这3类气溶胶EBR的湿度多项式函数[6]。一些研究还尝试在函数中进一步加入污染物浓度、气象因子等更多变量[7]。这种基于函数拟合的方法主要是通过建立EBR与相对湿度等变量的统计关系,在特定区域可能会有较高的精度,但不同区域的适用性尚不足,且其中的物理意义仍需进一步阐明。
被动光学遥感仪器通过接收自然光源在大气中的辐射,可以直接反演气溶胶的光学特性参数。但所获得的光学特性中并不包括消光系数、后向散射系数及EBR,需要先从光学特性反演其微物理特性,再根据微物理特性计算EBR。
相比于被动光学遥感,主动光学遥感仪器和积分浊度计采用主动光源,可以直接反演气溶胶的消光和后向散射系数,进而获得EBR。积分浊度计是用于测量气溶胶消光特性的高精度原位仪器,可以测量气溶胶的体散射系数,并基于朗伯-比尔吸收定律计算气溶胶的消光系数[8]。为了实现对后向散射系数的测量,Doherty(1999)采用方向性好的激光作为光源来改进积分浊度计,将散射角度提高到176◦∼178◦,进而估算EBR[9]。探测气溶胶的主动光学遥感仪器主要是激光雷达等[10]。激光雷达通过发射激光并接收后向散射回波信号,可以反演具有高度分辨率的气溶胶消光系数、后向散射系数及EBR。
3 光散射模型法
光散射模型是研究气溶胶产生光学散射现象的重要理论工具,也是主被动光学遥感仪器反演气溶胶光学和微物理特性的算法基础[11]。
如图2所示,不同的气溶胶粒子由于其形状、大小和复折射率不同,其散射光在立体空间中将有不同的分布。为了模拟粒子的光散射特性,德国科学家Mie在1908年通过电磁波的麦克斯韦方程给出了任意尺寸和成分的均质球形粒子散射问题的精确解,即著名的米散射理论[1]。然而,实际的气溶胶粒子并不是典型的球形,一些气溶胶如沙尘粒子甚至包含了大量的非球形颗粒。美国科学家Dubvoik等人用椭球模型模拟沙尘等非球形粒子,并用T矩阵法(T-Matrix Method,TMM)计算其散射光场[12]。一些复杂气溶胶模型(多球聚集体、立方体等)一般使用离散偶极子近似法(Discrete Dipole Approximation, DDA)[8]或有限差分时域法(Finite-Difference Time-Domain,FDTD)[13]计算其光学特性。对于冰晶等大尺寸粒子,为了加快计算速度,一般使用改进的几何光学方法(Improved Geometric Optics Method, IGOM)近似计算其光散射特性[8]。
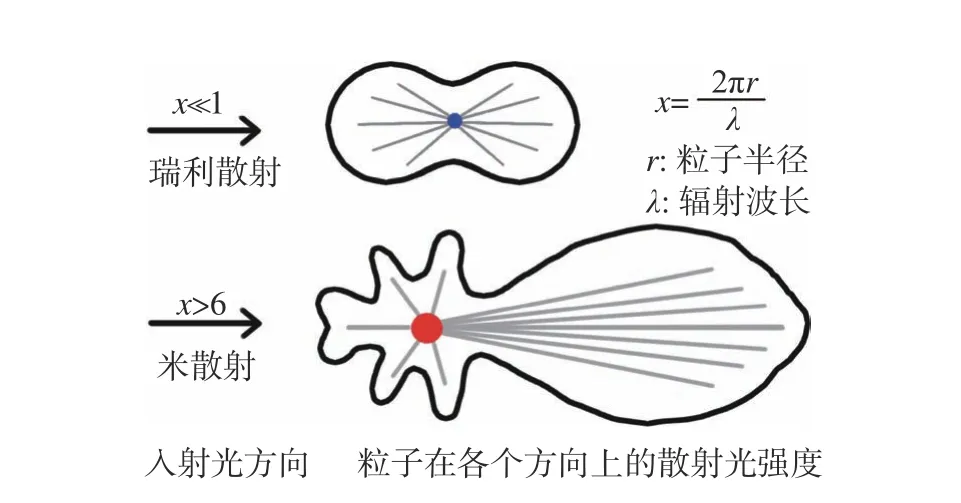
图2 不同粒子对光的散射示意图Fig.2 Schematic diagram of light scattering by different particles
目前对于气溶胶的形状尚未有明确的结论,且现有的非球形粒子光散射特性分析算法对于较大尺度粒子的计算十分耗时,因此米散射理论仍是近似计算气溶胶光学特性的主流方案。
真实大气中气溶胶是具有一定尺度谱和形状分布的集合体,其整体光学特性由单个粒子的光学特性按照粒子尺度谱的分布加权决定[14]:

式中, αa和 βa分别是气溶胶消光系数和后向散射系数,r为粒子半径,rmin和rmax是粒子粒径的分布范围,σe(r) 和 σπ(r)分别是气溶胶消光截面和后向散射截面,dN(r)/dInr是粒子的数浓度随粒子半径变化的函数。在米散射理论中,σe(r) 和σπ(r)可由粒子半径和复折射率计算出;对于非球形粒子,则还应当考虑其形状因素。
根据定义,气溶胶的EBR值Sa可联合以上两式求得:

在实际应用中,可通过原位测量或气溶胶模式来得到气溶胶粒子的微物理特性。原位测量精度较高,常作为遥感探测数据的参考和验证,但受限于采样时间和范围,无法在大范围内快速应用。气溶胶模式可在城市、全球尺度上提供气溶胶微物理特性,具有重要价值,但现阶段由于排放源资料不足、物理化学机制复杂、计算机算力有限等因素,导致模拟数据的准确度、时空分辨率较低,还处在与主被动光学遥感数据相互对比验证阶段[15]。
总体来说,光散射模型法能反演任意波段的EBR,且便于探究EBR和其他光学特性参数或微物理特性参数之间的函数关系,是理论研究的理想工具。但在实际应用中,需要通过原位测量或气溶胶模式为其提供真实环境中的气溶胶微物理特性,而这两者分别在时空尺度及数据精度上具有局限性。此外,对非球形粒子的形状建模及计算也是光散射模型法目前面临的一个瓶颈。
4 被动光学遥感法
遥感技术开启了大范围、快速、连续探测大气的新时代,为实现大气科学在全球和区域化范围内的应用发展提供了重要数据支撑,在卫星、计算机等新技术推动下,已成为大气科学的关键技术支柱之一[16]。
20世纪的大气气溶胶遥感探测以被动光学遥感为主。被动光学遥感仪器以太阳和天空辐射为信号源,通过多波段、多角度及偏振信息,可以反演气溶胶的大气柱积分光学特性参数和微物理特性参数[1]。其反演气溶胶微物理特性的算法均可归纳为解决以下问题[17]:

式中,y表示遥感能获得的多角度、多波段以及偏振信息,F表示矢量辐射传输模型,x是气溶胶微物理特性,e是误差项。建立矢量辐射传输模型的难点在于多次散射的计算、非球形粒子的散射特性计算以及散射查找表的建立。对矢量辐射传输模型的反演一般使用非线性最小二乘拟合、最优估算或正则化等统计学方法。
根据仪器所处的探测平台和反演原理,探测气溶胶的被动光学遥感仪器一般可分为地基和星载两大类[1]。图3是大气辐射传输示意图,从图中可见这两类遥感仪器主要的区别在于地基被动仪器受地表反射作用影响小,而星载被动仪器受地表反射率的影响大。

图3 大气辐射传输示意图Fig.3 Schematic diagram of radiation transmission
4.1 地基太阳光度计反演法
地基被动光学遥感仪器有宽带分光辐射计、多波段太阳光度计、太阳华盖辐射计等,其中以多波段太阳光度计的应用最为普遍[1]。
地基太阳光度计接收的大气辐射可以用平面平行大气向下扩散辐射的角分布表示[1]:
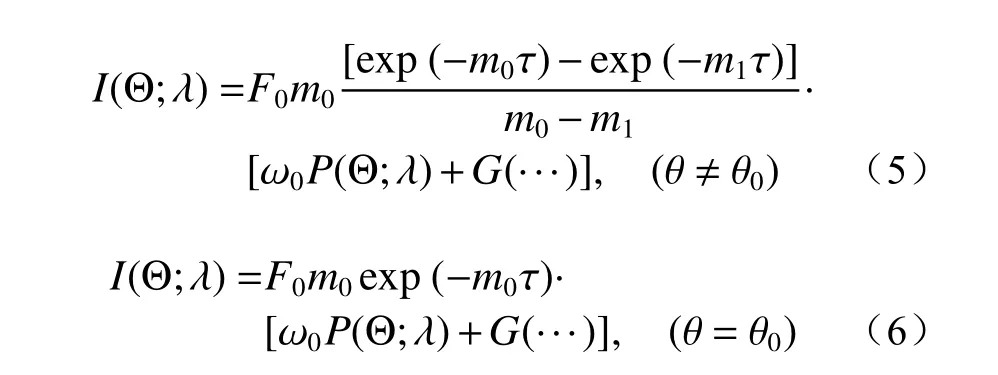
式中,I(Θ;λ)是 在散射角 Θ 方向接收到的λ 波长处的辐射量,θ0是 太阳天顶角,θ 是观测天顶角,F0是大气层外入射的光通量,m为大气质量数(m0≈1/cosθ0,m1≈1/cosθ ), τ=τext(λ)是光谱消光光学厚度, ω0是 单次散射反照率,P(Θ;λ) 是波长λ 处的相位函数,G(···) 是 与观测角度、地表反射、 ω0、P(Θ;λ) 及τ 有关的描述多次散射效应的函数。
在上述方程中,空气分子的相关参数可通过大气模型或仪器探测得到,地表反射率可以预先设定且其对地基仪器的影响较小。因此,I(Θ;λ)主要受气溶胶的光学厚度(Aerosol Optical Depth,AOD)(λ)、 单次散射反照率及相位函数Paer(Θ;λ)这3个光学特性参数影响。根据光散射理论,这3个光学特性参数可由气溶胶的微物理特性进一步表示,在米散射理论中可根据大气柱中粒子数随半径的分布函数 dNtot/dr以及粒子复折射率m˜求出,最终可得到地基观测辐射量与气溶胶微物理特性参数之间的函数关系:
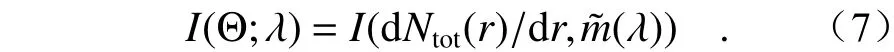
根据上述函数模型,可以从太阳直接辐射和多角度天空辐射反演大气柱积分的气溶胶粒子尺度谱分布、非球形粒子百分比、细粒子百分比(Fine-Mode Fraction, FMF)等微物理特性参数,以及AOD、复折射率、单次散射反照率、相位函数、EBR等光学特性参数[12]。
太阳光度计仪器轻便可靠,能够在野外无人值守时长期自动观测,独立反演出大气柱平均的EBR值,但仪器依赖于太阳光源提供辐射,且EBR值缺少高度信息。太阳光度计的反演算法中耦合了光散射模型,因此也受到目前非球形粒子的建模及算法不完善的影响。此外,尽管太阳光度计广泛应用于全球各类气溶胶观测网站中,但受限于地基站点的形式,无法在全球尺度上形成高精度的覆盖。
4.2 星载被动光学遥感反演法
星载被动光学遥感探测气溶胶的工作始于20世纪70年代中期,是卫星技术在光学探测应用上的时代产物,实现了对气溶胶在全球尺度上的遥感探测。其应用代表有基于多光谱和多角度观 测 的MODIS (Moderate Resolution Imaging Spectroradiometer)、MISR (Multi-angle Imaging SpectroRadiometer),以及在此基础上加入了偏振探 测 信 息 的POLDER (POLarization and Directionality of the Earth’s Reflectances)[16]等。的作用[1]。卫星观测到的大气顶部反射率 ρ可以表示为:
与地基被动遥感不同,星载被动遥感接收到的辐射值中地表反射率的作用不可忽略,因此其反演算法需要同时考虑地表反射率和大气气溶胶

式中, ρAtm为 大气的路径辐射项等效反射率, ρG为地表二向反射率,ϕ为相对方位角,S为大气下界的半球反射率,TAtm为大气透过率。
为了减少与大气状态有关的参数,星载被动遥感的反演算法一般根据经验假定几组不同的气溶胶模式,使用辐射传输软件按照设定的参数预先计算好查找表,通过与观测值匹配,查找出最优的气溶胶光学厚度和气溶胶模式(粒子尺度谱分布和复折射率)。其反演误差主要来自于对地表反射率的估计和气溶胶类型的假设[16]。根据光散射模型法,可以计算相应气溶胶模式下的EBR值。
针对不同的地表类型、气溶胶组分及传感仪器,星载被动遥感算法主要包括多角度遥感法、偏振特性遥感法、暗像元法、结构函数法、深蓝算法、地表反射率库支持法、以及新兴的深度学习法等[18-19]。
与地基被动遥感相比,星载被动光学遥感法的优势在于能获取全球范围内的EBR数据,缺点在于其使用查找表法反演的气溶胶模式误差较大。因此,并不建议以此来计算准确的EBR值,但可作为研究全球范围内EBR值变化趋势的一个参考[20]。
5 激光雷达法
主动式的激光雷达技术要比被动光学遥感复杂得多,但其具有高探测分辨率和高探测精度的独特优点,已成为观测大气气溶胶垂直分布的重要工具[21]。近年来随着激光雷达在大气气溶胶探测领域内的快速发展,气溶胶EBR(又称激光雷达比)愈发成为研究热点。
激光雷达通过向大气发射脉冲激光,接收激光与大气粒子相互作用的后向散射回波信号来反演气溶胶的状态参数。如图4所示,激光在大气中传输时,与大气分子和云-气溶胶分别在入射波长附近产生瑞利散射和米散射这两种弹性散射,并与氮气、氧气等多种气体在偏离入射波长处产生纯转动拉曼散射和振动-转动拉曼散射这两种非弹性散射。不同种类的激光雷达主要区别之一在于其接收的散射光谱不同。目前用于探测气溶胶的激光雷达主要有米散射激光雷达、拉曼激光雷达和高光谱分辨率激光雷达(High Spectral Resolution Lidar, HSRL)等。
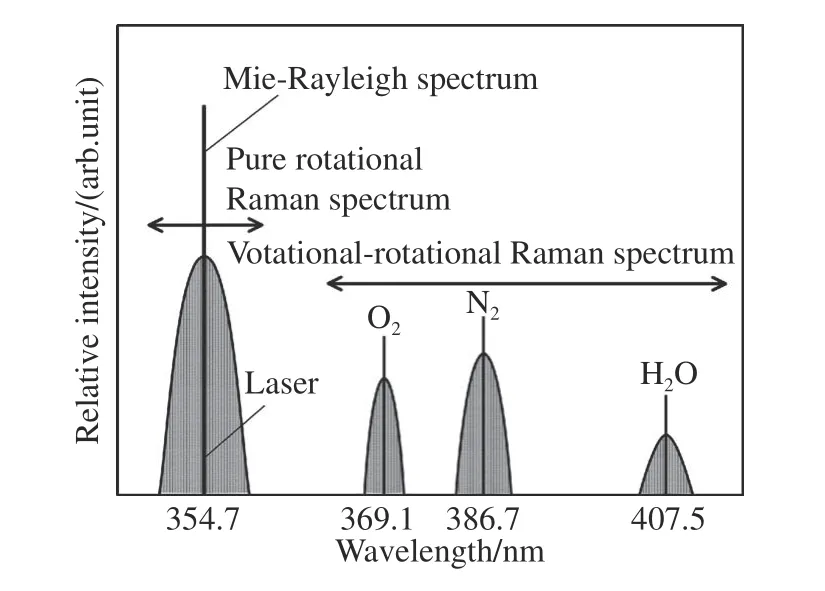
图4 入射激光波长为354.7 nm时的激光雷达大气回波信号光谱分布Fig.4 Spectral distribution of return signals of Lidar when incident wavelength is 354.7 nm
5.1 米散射激光雷达的约束反演法
米散射激光雷达是早期出现的一种激光雷达,其结构简单、成本低,广泛应用于气溶胶的探测[22]。米散射激光雷达接收的大气后向散射回波信号PL(z,λL)可以表示为:
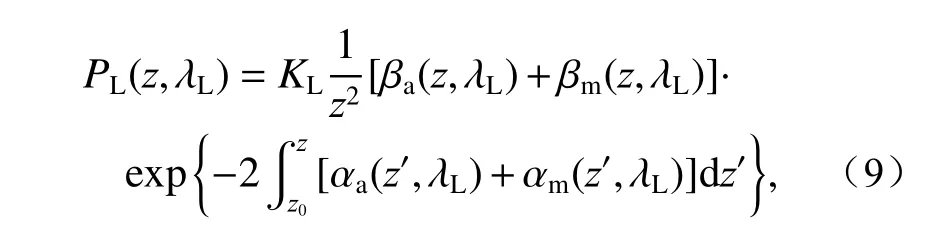
式中,下标“a” 和“m”分别表示气溶胶和分子,L表示米散射通道,KL是米散射通道的系统常数,z表示回波信号返回的高度,z0表示激光雷达所在的 高 度, λL表 示 激 光 发 射 波 长, αa(z,λL)和βa(z,λL)分 别代表在高度z处 、波长 λL上的气溶胶消光系数和后向散射系数, αm(z,λL)和 βm(z,λL)分别代表在高度z处 、波长λL上的大气分子消光系数和后向散射系数。
单个米散射激光雷达方程中存在 αa(z,λL)和βa(z,λL)这两个未知数,因此求解该方程在数学上是一个欠定问题。对该方程求解的经典方法如斜率法、Klett法以及Fernald法等都需要假定大气消光系数与后向散射系数之间的关系[3]。
为了解决单个米散射激光雷达无法反演EBR的问题,发展出了场景分类法、AOD约束法、双流法以及双波长法等具有一些额外约束的方法来帮助米散射激光雷达反演出具有一定准确度的EBR。
5.1.1 场景分类法
场景分类法根据激光雷达的观测值和地表类型来确定气溶胶类型,再分配相应的气溶胶层平均EBR值,主要应用于星载云和气溶胶米散射激光雷达CALIOP(Cloud-Aerosol Lidar with Orthogonal Polarization)等的气溶胶反演中。
如图5所示,CALIOP利用层积分后向散射系数 γ′、 退偏比、层积分色比 χ′这3个米散射激光雷达可以获得的光学参数,以及层次高度和地理信息对气溶胶进行预分类。目前CALIOP版本4气溶胶分类算法中将气溶胶共分成11个子类,并参考地基气溶胶被动遥感观测站点AERONET(AErosol RObotic NETwork)多年统计分析后的数据建立了EBR值查找表[4]。

图5 CALIOP版本4的平流层气溶胶分类算法Fig.5 Stratosphere aerosol classification algorithm for CALIOP version 4
场景分类法适用性好、程序效率高,为CALIOP反演大规模的气溶胶数据提供了有效的EBR值。其限制主要来自于两个方面:一是CALIOP基于经验使用有限的观测值和地表类型对气溶胶进行预分类,存在一定的误判;二是每类气溶胶的EBR可能具有相当大的自然变化范围。因此CALIOP查找中的值具有30%左右的误差[4]。
5.1.2 AOD约束法
AOD是气溶胶消光系数在一段距离上的积分。AOD约束法以层积分AOD为约束来帮助米散射激光雷达反演出相应的层平均EBR。Fernald于1972年从米散射激光雷达信号方程中推导出气溶胶层恒定EBR值和AOD之间的关系式是一个超越方程[3]:

式中,与光学参数有关的波长都是λL,为了简化符号在方程中略去,zb和zt分别是气溶胶层的层底和层高,A OD(zb,zt)是 整层气溶胶的AOD,AOD(zb,z)包括层底到任意高度之间的AOD。
层积分AOD一般通过与激光雷达时空同步的星载或地基被动光学遥感仪器得到;少数情况下,当气溶胶层上、下都有干净大气时,还可通过信号廓线和大气分子拟合得到[23]。
超越方程一般没有解析解,只有近似解或数值解。近似的解法有CALIOP算法中应用的梯形近似法[23]以及美国科学家Damien提出的一种忽略长波长处大气分子影响的近似法[24]。数值解则可以通过在Fernald解中代入不同的Sa,计算出相应的层积分AOD,并与已知的层积分AOD比较来寻找两者最匹配的Sa值,具体有穷举迭代法[25]、二分迭代法[26]以及不动点迭代法[27]等。近似解在批处理CALIOP这类大体量数据时具有更高的效率,但数据精度受近似条件影响;迭代法的时间效率相对较低,但可以通过设置阈值来控制误差大小,适用于分析具体的气溶胶观测案例。
米散射激光雷达独立获取AOD的可应用场景较少,因此该方法一般通过联合主被动仪器实现,也是目前较为流行的一种方法。被动光学遥感还具备反演气溶胶尺度谱的能力,可以进一步为激光雷达提供粗、细模态的AOD并反演出相应模态的EBR[28]。但被动光学遥感一般只能提供白天的数据,且当大气中存在多层气溶胶时无法区分层AOD,因此具有一定的局限性。
5.1.3 双流法与双波长法
除了主要由CALIOP使用的场景分类法及应用较为广泛的AOD约束法外,研究者们还尝试开发了一些其他的算法来帮助米散射激光雷达反演气溶胶EBR,如双流法和双波长法。
双流法是指两个弹性后向散射激光雷达从相反方向对同一大气柱同时进行测量,通过增加方程数量来解决米散射激光雷达反演中的欠定问题[29]。在实际应用中,实现双流法需要两个米散射激光雷达从高空和地面同步测量同一大气柱,而现有的星载激光雷达或机载激光雷达无法在同一地基站点上空长时间停留,因此该方法目前受限于应用场景,相关研究和报道较少。
双波长法是指假设在气溶胶层中不同波长的气溶胶后向散射系数(或消光系数)廓线形状具有相似性,以此为约束来反演气溶胶EBR[30]。双波长法适用于多波段的米散射激光雷达,该算法计算量大,且该方法的假设也会引入一定误差,故应用实例也不多。
5.2 拉曼激光雷达反演法
为了解决单个米散射激光雷达中“一个方程,两个未知数”的欠定问题,拉曼激光雷达在米散射激光雷达的基础上,增加了一个接收拉曼分子散射的信号通道,并联合米散射信号通道一起反演气溶胶的消光系数和后向散射系数。
如图4所示,在入射波长附近的频移光谱是纯转动拉曼光谱,其与分子的转动能级有关;而离入射波长距离更远的频移是振动-转动拉曼光谱,中心频移量与具体分子的振动能级有关。空气分子的振动-转动拉曼后向散射截面很小,通常为10−32~10−28cm2·sr−1,而其纯转动拉曼后向散射截面则要比前者大3个数量级[31]。
5.2.1 振动拉曼法
振动拉曼法由德国科学家Ansmann于1990年提出,在1992年首次实现振动拉曼-米散射激光雷达对云的观测[32],是目前应用最广泛的拉曼算法。
拉曼散射的光强度与散射分子的数密度成正比,氮气在大气中混合均匀且含量高达78%,因此拉曼通道一般选取接收氮气分子的振动拉曼散射回波信号。拉曼通道接收的信号PR(z,λR)可以表示为[32]:

式中,下标 R 表示拉曼通道, λR表示振动拉曼波长,KR是振动拉曼分子通道的系统常数,βR(z,λL)是氮气分子在波长λL处产生的振动拉曼后向散射系数, αa(z,λR)和 αm(z,λR)是气溶胶分子和大气分子在波长λR处的消光系数。
和大气分子有关的参数可以通过气象探空数据或标准大气模式得到。此外,还需假设αa(z,λR)和 αa(z,λL)之间的比值恒定:

式中,k是大气气溶胶的Angstrom指数,一般取典型值1代入,当k的实际取值在0.8到1.2之间时将引起1%左右的的误差[32]。
大气气溶胶的消光系数可以通过对拉曼通道信号进行微分求出,后向散射系数可通过联合米散射通道信号和拉曼通道信号求出,从而得到气溶胶EBR值的高度廓线[32]。
振动拉曼通道信号信噪比低,又是使用微分法求解的消光系数,因此误差高达20%左右[32],因此一些研究提出使用统计学中的正则化法和最优估计法来提高反演精度[33]。
振动拉曼法能独立反演出较高精度的EBR高度廓线,且由于振动拉曼光谱与入射光波段不重合,对光谱分辨能力的要求相对较低,拉曼激光雷达近年来发展迅速并已有较好的产业化应用。但由于振动拉曼信号比瑞利散射信号小3~4个数量级,信噪比低,导致振动拉曼激光雷达一般只在夜间进行观测,且由于分子的瑞利散射信号与波长的四次方成反比,长波段信号的信噪比更低,故该方法尚未在1064 nm波段应用。
5.2.2 转动拉曼法
转动拉曼散射截面比瑞利散射截面只低几个百分点,其信号强度高于振动拉曼,因此韩国原子能研究所的Kim和Cha(2005)提出了基于纯转动拉曼光谱的转动拉曼法测气溶胶[31]。纯转动拉曼光谱的中心波长没有偏移,因此该方法不需要对k进行假设。纯转动拉曼通道的信号PRo(z,λL)可以表示为:
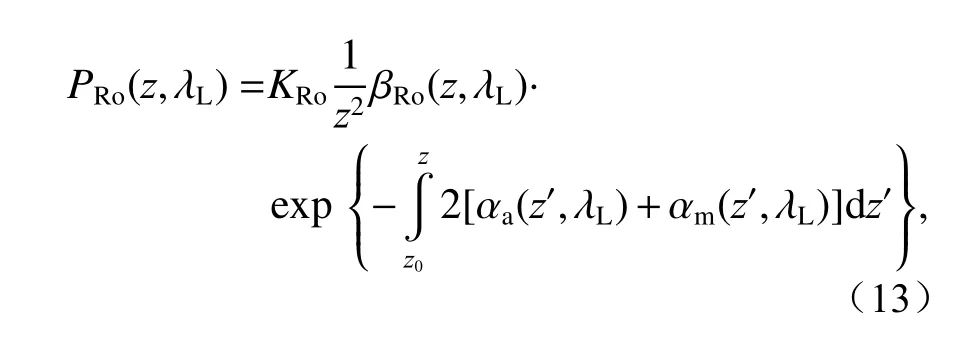
式中,下标R o表 示转动拉曼通道,KRo是纯转动拉曼分子通道的系统常数, βRo(z,λL)是大气分子在波长λL上产生的纯转动拉曼后向散射系数。
与振动拉曼法类似,通过对式(13)求导可以反演出气溶胶消光系数,联合纯转动拉曼通道信号和米散射通道信号可以反演出气溶胶后向散射系数,并得到气溶胶EBR值的高度廓线。
相比于振动拉曼法,转动拉曼法的优势是信噪比高,且不需要对k进行假设,缺点是由于转动拉曼的光谱中心与弹性散射重合,因此对于分光系统的分辨能力和抑制比要求较高。目前该技术的应用还相对较少,德国莱比锡莱布尼茨对流层研究所的Moritz(2016)首次使用转动拉曼法实现了1064 nm处EBR高度廓线的反演[34]。
5.2.3 拉曼AOD法
由于振动拉曼信号在白天信噪比太低,在求导过程中会引入较大误差,因此提出了使用拉曼通道提供的AOD来约束EBR反演的方法[25]。具体的AOD约束反演法在5.1节中已有介绍。根据公式(11),拉曼分子信号通道可以计算出在探测范围内任意高度间的A OD(z1,z2,λL):
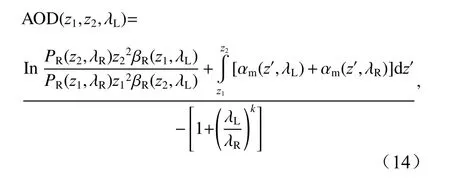
式中,z1和z2是拉曼通道可探测到的气溶胶层区域内任意两个高度。
相比于被动光学遥感,拉曼通道具有可以计算同一大气柱中多层AOD的优势,但其探测高度与精度相对有限。该方法一般作为白天振动拉曼激光雷达探测大气的补充算法。
5.3 HSRL反演法
早在20世纪60年代末,国际上就开始展开对HSRL的相关研究[35]。HSRL的反演原理与拉曼激光雷达相似,其在米散射激光雷达的基础上,通过光谱鉴频器分离出大气分子的瑞利散射回波信号,并联合米散射通道信号一起反演气溶胶的消光系数和后向散射系数。大气分子的瑞利散射信号强于拉曼分子散射信号,因此相对于拉曼激光雷达,HSRL探测的信噪比及反演精度更高。但如图6所示,两种弹性散射信号的中心波长重合且频谱很窄,使得仪器对光谱分辨能力的要求也更高。

图6 激光雷达后向散射信号频谱。(a)标准后向散射激光雷达;(b)HSRL中附加的频谱识别Fig.6 Spectra of lidar backscatter signal.(a) Standard backscatter lidar; (b) additional spectral discrimination in HSRL
HSRL接收到的空气分子瑞利散射回波信号Pm(z,λL)为:

式中,Km表示大气分子瑞利散射通道的系统常数。大气气溶胶的消光系数可以通过对大气分子通道信号进行微分求出,后向散射系数可通过联合米散射通道信号和大气分子通道信号求出,从而得到气溶胶EBR的高度廓线[34]。
HSRL的信号强度高出拉曼散射几个数量级,是未来发展星载激光雷达方案的首选。但HSRL技术也存在一些技术瓶颈与挑战,其中一个主要瓶颈就是缺乏多波长通用、稳定可靠的光谱鉴频技术。目前HSRL的光谱鉴频器主要有原子/分子吸收池和干涉型光谱鉴频器两大类。原子/分子吸收池对入射光的角度不敏感,其稳定性好且对吸收线的抑制性高,但只在特定波段具有滤光属性,干涉型光谱鉴频器可以应用到任意波长的光谱鉴频,常见的FPI对波长适应性较好但量子效率不高[36]。最近,浙江大学刘东团队针对新型的HSRL鉴频器——视场展宽麦克尔逊干涉仪(Field-widened Michelson Interferometer, FWMI)的研制取得了一定突破和进展,为实现HSRL准确、稳定探测气溶胶的光学特性和EBR提供了较大帮助[35-36]。
6 讨论与展望
EBR是单个米散射激光雷达反演气溶胶特性算法中的一个关键光学参数,且在气溶胶分类中具有重要参考价值。根据气溶胶微物理特性和光学特性之间的联系,发展出了相应的光散射理论及主被动光学遥感等探测方式,并由此衍生出反演气溶胶EBR的光散射模型法、被动光学遥感法、激光雷达法等。
光散射模型法可以模拟气溶胶的所有光学特性,是研究EBR与其他物理光学参数之间联系的理论工具。在实际探测中,光散射模型法常与原位仪器结合反演,作为外场实验结果的高精度对比。原位仪器逐点探测的方式效率较低,而主被动光学遥感的发展则实现了大气气溶胶的快速、大范围探测。被动光学遥感只能探测整层大气柱的气溶胶特性,其中地基太阳光度计的反演数据可信度较高,而星载被动光学遥感则在全球覆盖度上具有优势但反演精度不高。激光雷达作为光学遥感的后起之秀,可以获取大气颗粒物的高精度、高灵敏度垂直廓线信息,是探测气溶胶立体分布的重要手段。激光雷达的反演精度与其对光谱的分辨能力成正相关:米散射激光雷达只有一个通道故无法独立反演EBR;拉曼激光雷达通过增加较易分辨的拉曼散射光谱实现了EBR垂直廓线的反演,但拉曼光谱信号相对较弱,在日间探测等方面仍有较大的提升空间;HSRL使用信噪比较高的分子散射信号提升了EBR反演的精度,但其高光谱分辨率的要求也造成了其技术复杂、仪器成本高的应用壁垒。
总体来说,气溶胶EBR的反演方法各有千秋,并没有最佳的方案能以一概全,多种方法联合反演是有利于同时发挥各类仪器和算法优势的一个探究方向。随着21世纪数字化大气战略的推进,模式及主被动光学遥感在仪器、算法及数据层面上将进一步组网与融合,也将为联合反演气溶胶EBR创造更有利的条件。
上述关于EBR的反演方法不仅适用于气溶胶,对云也同样具有借鉴意义。目前对云的微物特性已有大量研究,为使用光散射模型反演其EBR创造了良好条件;许多主被动光学遥感能够同时探测云和气溶胶,其中激光雷达测云EBR的方法和气溶胶基本相同。但相比于气溶胶,云的粒子致密度更高、粒子尺寸更大,因此在反演时还要考虑多次散射的影响[27]。
