Polar码编译码技术研究

鲁信金，舒冰心，雷 菁

(国防科技大学 电子科学学院，湖南 长沙 410000)

0 引言

通信系统中信道干扰和噪声总是影响系统的可靠性，信道编码技术可用最小代价来提升通信系统可靠性。1948年，香农(Claude Shannon)在《通信的数学理论》[1]中指出对于去认定的信道容量，当码率小于其信道容量时，总是可以找到一种编码方案使得码长足够大时，使用最大似然译码可使误码率任意小，这奠定了纠错编码理论的基础。此后，很多学者致力于研究设计出能够逼近信道容量(也即香农界)的实用编码方案，如线性分组码[2]、卷积码[3]和代数几何码[4]。进入20世纪90年代，信道编码进入了第一次快速发展的阶段，研究的重点集中为Turbo码[5]和LDPC码[6]，随后二者在实际的通信系统得到了广泛的应用和很深入的研究，虽然这两种编码没有达到理论证明的香农限，还具有很高的复杂度，但依然备受青睐。

近年来，无线通信物理层中的编码领域发展较慢。在2009年，E.Arikan等人研究了信道极化问题，根据信道极化提出了极化码[7]。不仅证明了极化码在二进制离散无记忆信道(Binary Discrete Memoryless Channel,BDMC)下，可以达到信道容量，还提出了具有低复杂度的编码和译码方案。R.Moil和T.Tanaka[8]针对任意对称二进制无记忆信道提出了一个新的被证明可实现的编码构造方法。编码构造方面对于不同的信道，Bhattacharyya参数的计算和信息位选择方法是不同的，而很多学者研究了很多适用于不同信道的信息位选择的方法，如蒙特卡洛迫近法、密度演化构造方法等。

对于信道编码而言，译码算法的复杂度和性能至关重要。自极化码提出后就受到大量学者对其译码算法进行研究。目前polar码译码算法主要有SC算法[9]、SCL算法[10]、CA-SCL算法[11]、BP算法[12]、SCAN算法[13]，以及各种算法的简化版本[14-16]。其中SC算法最初由Arikan提出，但其在码长有限长情形下，性能一般。SCL是SC算法性能提升的改进版本，原理是在SC的基础上提供了多条路径；而CA-SCL是在SCL的基础上对信息比特进行了循环冗余校验，它通过简单的校验就可以带来性能的极大提升。目前基于CA-SCL译码算法，polar码性能已经优于LDPC码。SC、SCL以及CA-SCL算法均是硬输出算法，即最终输出的是0、1比特序列，而不是对应的LLR值。为了在一些联合设计中使用polar码，就必须提供polar码的软输出算法，即输出对应比特的LLR值。BP和SCAN算法就是软输出算法，由于BP和SCAN算法在消息传递和递归规则上不同，导致了两种算法的译码延时和收敛速度不同。译码延时上，BP消息传递采用“洪水”规则[17]，SCAN采用类SC算法的串行消除规则，因此BP算法的译码延时好于SCAN算法。SCAN算法1次迭代就能达到稍好于SC算法的性能，一般而言，BP算法需要40～50次的迭代过程，而SCAN算法1次迭代就能达到稍好于SC算法的性能。性能上几种算法排序为：CA-SCL>LDPC>SCL>BP=SCAN>SC。

从极化码被广泛关注研究之后，极化码逐渐应用在现代通信系统中以及不同信道场景中，如二进制对称信道、混合信道、非对称信道、非二进制信道、多址接入信道、并行信道、高斯信道以及瑞利信道等。

1 信道极化原理

polar码的基本原理是信道极化。信道极化是这样的一种现象：对二进制对称信道进行特定的“组合”和“拆分”，则拆分后的“比特信道”将呈现极化现象，即一部分“比特信道”的对称信道容量趋近于1，而其余部分“比特信道”的对称信道信道容量趋近于0。如果发送端将源信息比特放置在“好的比特信道上”，而在“坏的比特信道上”放置固定比特(如0)，同时在接收端采用连续消除译码算法，在码长N→∞ 时将可以达到信道容量。虽然基于二进制离散无记忆信道提出了信道极化，但是信道极化的现象是普遍存在的，除B-DMC信道外其他信道也存在此现象，而信道极化包括信道组合和信道分解两个重要过程，接下来对其进行介绍。

1.1 信道组合

在物理信道W(y|x)上连续发送N个符号，若发送端对这N个符号进行特定方式的组合，则等效于信道W的组合。

如图1所示，对发送的信息源符号以一定方式进行组合，并记组合后的信道为W2(y1,y2|u1,u2)，则：

W2(y1,y2|u1,u2)=W(y1|u1⊕u2)W(y2|u2)。

(1)

进一步将两个W2信道组合为W4信道，依次往复，直至递归到两个WN/2信道组合为WN信道，如图2所示。其中,RN是置换矩阵，其满足RN:(v1,v2,…vN)→(v1,v3,…vN-1,v2,v4,…vN)。

图1 W2信道Fig.1 Channel W2

图2 WN信道Fig.2 Channel WN

1.2 信道拆分

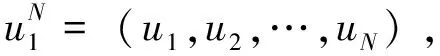
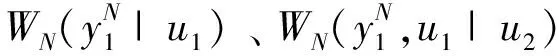
(2)

可以将上式迭代的形式，保证极化码的编码和译码具有线性复杂度。图3展示了N=8时，信道W8分解的过程：独立的8个信道W通过信道组合之后可以得到一个信道W8，信道分解时，信道W8先分解为两个相互独立的信道W4，之后信道W4分解为两个相互独立的信道W2，最后信道W2分解为两个相互独立的信道W，因此信道分解是一个递归的过程。

图3 N=8信道分解Fig.3 Channel decomposition(N=8)

1.3 信道极化定理

polar码选择在“比特信道”量为1的比特信道上发送信源信息(比特信道容量为0的比特信道上发送固定信息，如0)。当信道W为二进制删除(Binary Erasure Channel，BEC)信道时，图4是码长N=210删余概率ε=0.5时仿真结果图，图4(a)是信道极化现象的仿真，图4(b) 是各信道容量占比统计柱状图。图5是N=220，删余概率ε=0.5时的仿真结果图，图6是N=220,删余概率ε=0.3时的仿真结果图。

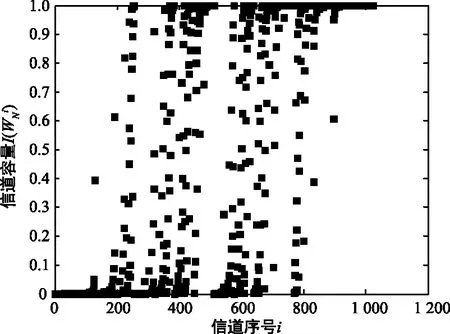
(a) 信道极化

(b) 各信道容量占比统计柱状图图4 N=210,ε=0.5时信道极化现象及各信道容量占比Fig.4 Channel polarization phenomenon and the proportion of each channel capacity when N=210,ε=0.5

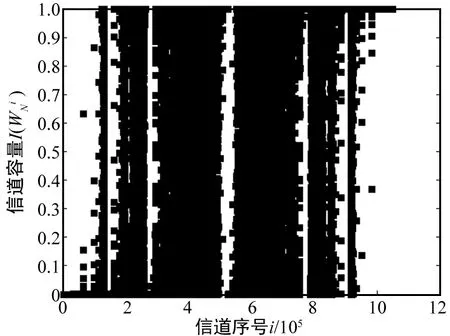
(a) 极化现象

(b) 各信道容量占比图5 N=220,ε=0.5时信道极化现象及各信道容量占比Fig.5 Channel polarization phenomenon and the proportion of each channel capacity when N=220,ε=0.5

(a) 极化现象

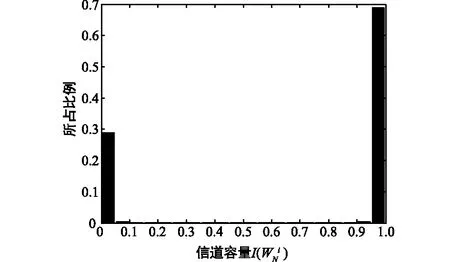
(b) 各信道容量占比图6 N=220,ε=0.3时信道极化现象及各信道容量占比Fig.6 Channel polarization phenomenon and the proportion of each channel capacity when N=220,ε=0.3

图4和图5可以看出，当ε=0.5时，随着N的增大，信道容量为0和1的信道所占比例增大，信道极化的现象越来越明显。由图5和图6对比可以看出，当N=220，信道容量为0时的信道所占比例趋向于信道删除概率ε的值，信道容量为1的信道所占比例趋于信道删除概率1-ε，与上述定理所述一致。

基于信道极化的现象，选择其中较好的信道，即信道容量趋向于I(W)的信道作为信息位传输数据，而较差的信道，即信道容量趋向于1-I(W)的信道作为冻结位。运用该思想进行极化码的编码和译码。

2 polar码编码构造

polar码码长N→∞时，polar码可达信道容量。而实际编码过程中码长N不可能趋于无穷，因此polar码也不可能做到信道完全极化。总有部分“比特信道”的信道容量介于0和1中间。因此确定对称信道容量最大的K个“比特信道”是解决polar码码字构造的主要问题；其次，生成矩阵决定了信道重组的形式，信道重组的形式作用于待发送信息上的函数运算法则，经典的极化编码方案以二维核矩阵F=[1 0;1 1]为基底，迭代构造生成矩阵。

2.1 生成矩阵

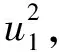
(3)

类似地，对于重组信道W4，其生成矩阵G4可以简化为G2的矩阵形式：

(4)

其中，⊗为Kronecker内积。继而推算出任意生成矩阵的递归表达式，即生成矩阵GN：

GN=F⊗log2(N),

(5)

其中,F=G2。考虑到连续消除算法的译码顺序，Arikan在生成矩阵中引入比特翻转置换操作：对于任意正整数i，定义(b1,b2...,bn)为其二进制表示，比特翻转操作rvsl(i)=(bn...,b2,b1)，对于任意矢量(v0,v1...,vn-1)，其比特翻转置换后的矢量为(vrvsl(0),vrvsl(1)...,vrvsl(n-1))，该操作可以用N×N维的置换矩阵BN表示。设BN中第i行第j列的元素为bi,j，则有：

(6)

则生成矩阵的一般形式为：

GN=BNF⊗log2(N)。

(7)

2.2 信息集

信息集是信息信道的索引集合，而信息信道的质量通常由对称容量及巴特查里亚因子所度量。对称容量与巴特查里亚因子是信道性质的相反描述度量，其中对称容量的计算复杂度更高，因此巴特查里亚因子更多地应用在实际系统中。在此，仅讨论基于巴特查里亚因子的信息集选取准则。

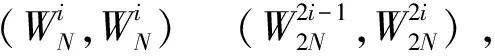
(8)

(9)

(10)

当且仅当物理信道为BEC时，式(8)及式(9)的等号成立，此时比特信道的巴特查里亚因子可迭代计算。但对于其他二进制信道而言，比特信道的转移概率计算复杂度较大，其巴特查里亚因子难以确定，当前较为常用的处理方法为近似迭代法。近似迭代法针对不同物理信道重定义了巴特查里亚因子，并使用近似迭代准则迭代计算比特信道的巴特查里亚因子。在此给出BSC、BAWGNC、BFC的巴特查理亚因子。

对于交叉概率为Pε的BSC，其巴特查理亚因子按原定义计算：

(11)

对于连续信道，其巴特查里亚因子的定义为积分函数：

(12)

对于二进制加性高斯白噪声(Binary AWGN,BAWGN)信道，根据定义计算其转移概率，其中σ2为噪声方差，调制方式为BPSK(Binary Phase Shift Keying)。

(13)

(14)

将式(13)与式(14)带入式(12),可得：

(15)

对于二进制衰落信道(Binary Fading Channel)，可将其近似为AWGN信道处理，则其转移概率为：

(16)

(17)

(18)

2.3 polar码编码

polar码实际上就是线性分组码，因此其编码过程和一般的线性分组码一样。不同的是一般的线性分组码根据码字汉明重量等挑选生成矩阵某些行(RM码根据的是最大汉明重量)，而polar码由信息比特集A确定生成矩阵的某些行。假设C为N比特长的码字，UI为K比特信源信息，UF=0为N-K比特固定信息，则：

C=UGN×N=UIGK×N+UFG(N-K)×N,

(19)

其中，GN×N是polar码生成矩阵，GK×N是根据信息比特集A中元素从GN×N中挑选的行组成矩阵。

3 polar码译码

3.1 SC译码原理

(20)

判定准则为：

(21)

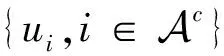
(22)

如图7所示，首先译码器计算标号为1的点的左消息LLR值，而此时必须知道标号为2和3点的LLR值，同理要计算2的LLR值应计算4和5的LLR值，而3需要计算6和7的LLR值，而4、5、6、7的LLR值可以直接根据信道传输过来的LLR值直接进行计算。通过以上递归过程则得到了1点的LLR值。此时先判定该点是否是固定比特，如果是固定比特则直接译为0；如果是信息比特，则根据刚计算得到的LLR值进行判决:LLR值大于0判为0、LLR值小于0判为1。同理直至SC译码器将u0～u7的LLR值全部计算出来，并判决得到比特值。

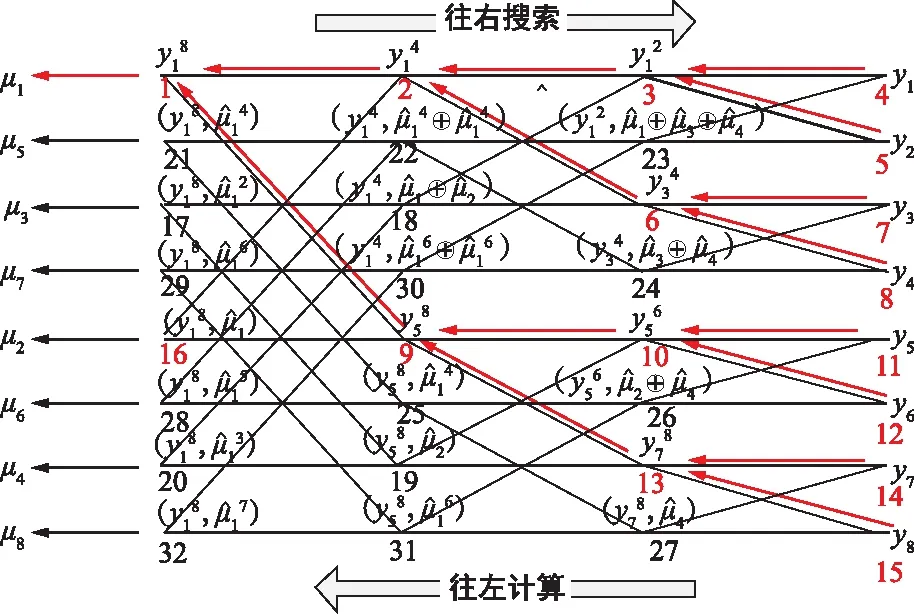
图7 递归顺序Fig.7 Recursive order

3.2 SCL译码算法

通过这种多路径译码策略，极化码在中短码长下的误码性能得到显著提高。当L足够大时，SCL算法的误码性能能够接近于最大似然(ML)算法。但是随着L的增加，SCL算法的复杂度也呈指数倍增长。其时间复杂度和空间复杂度均为O(LNlog2N)。所以，SCL算法仅适用于中短码长的情况，当码长N和译码路径数L足够大时，高复杂度的SCL算法难以实现。

图8 SCL译码Fig.8 SCL decoding

3.3 CA-SCL译码算法

CA-SCL算法相较于SCL算法而言，能够大幅降低译码复杂度。其需要对所有得到的译码结果进行校验，如果满足校验，则从中选取转移概率最大的译码路径作为最终译码结果；CA-SCL算法本具有较低的时延，但由于引入了再编码步骤，导致仍具有较大时延。然而，在时间复杂度以及空间复杂度上，CA-SCL算法相比于SCL算法都有较大改进。

4 仿真与分析

此处采用经典SC译码，选择BEC、BSC、AWGN三种信道进行仿真，仿真通过计算误码率来分析编译码方案的优劣。

4.1 BEC信道下极化码的仿真

4.1.1 不同删除概率及不同码率下

BEC信道删除概率p表示信道中传输符号在接收端无法识别的概率大小，在极化码中改变码率R通过改变极化信道的选择比例。图9为码长N=64时，误码率在删除概率和码率这两个参数变化时的变化曲线。横坐标为删除概率，不同颜色曲线对应不同码率R。

图9 当N=64时BER变化曲线Fig.9 BER change curve when N=64

由图9可知，每一条曲线变化趋势一致，随着BEC信道删除概率增大，误码率变大。这是因为在码长N和码率R固定时，随着BEC信道删除概率的增大，巴氏参数Z增大，信道极化现象变差，选择用来传输信息的子信道参数Z也增大，所以误码率增大。

比较不同颜色的4条曲线，码率R越大，误码率越大。这是因为当参数N及p一定时，极化信道巴氏参数Z的值确定。当码率R增大时，所选的子信道个数增大，此时会将参数Z较大的信道选择为传输信息的信道，将不好的信道选做信息位，造成误码的增加。

4.1.2 不同码长条件下

BEC信道中，码长N值越大，极化现象越明显，此时码率R=0.5、删除概率p=0.2，如图10所示，随着码长N的增大，误码率明显变小。这是因为当N值增大时，信道容量为0和1的信道总数增大，信道容量为其他值所占的总数减小，即极化的效果更加明显，此时巴氏参数Z的值向着0和1两个方向集中。所以当码长N增大时，选择用来传输信息信道的巴氏参数值更趋向于0，所以误码率减小。

图10 当p=0.2,R=0.5时BER变化曲线Fig.10 BER change curve when p=0.2,R=0.5

4.2 BSC信道下极化码的仿真

4.2.1 不同交叉概率下

BSC信道中信元符号按交叉概率的大小比例进行翻转。图11为误码率在BSC信道交叉概率p变化时的变化曲线，此时码长N=256和码率R=0.1。横坐标为BSC信道的交叉概率，纵坐标为误码率。

由图11可知，随着BSC信道交叉概率p的增大，误码率变大。很明显，此次仿真的误码率与BEC信道具有相似的特性，故造成这种结果的原因也与其相似，可以总结为：在码长N和码率R固定时，随着BSC信道交叉概率在0～0.5的范围内增大，巴氏参数Z增大，信道极化现象变差，选择用来传输信息的子信道参数Z也增大，所以误码率增大。

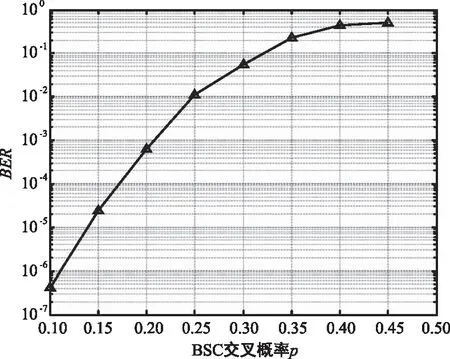
图11 当N=256,R=0.1时BER变化曲线Fig.11 BER change curve when N=256,R=0.1

4.2.2 不同码率下

取N=256，p=0.2，图12为极化码在不同的码率条件下的误码率曲线。随着码率R的增大，误码率明显变大。曲线的变化趋势与BEC信道的结果相似，但从仿真结果可以看出,当误码率小于0.15时，误码率才小于1/100。所以BSC信道中可用的码率范围很小，一个码字可以传输的信息有限。BSC信道中不同码长N的情况下，误码率与BEC信道具有相似性，随着码长N的增大，误码率明显变小。

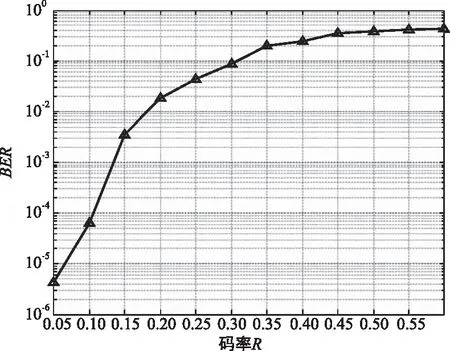
图12 当N=256,p=0.2时BER变化曲线Fig.12 BER change curve when N=256,p=0.2

4.3 AWGN信道下极化码的仿真

虽然极化码是基于B-DMC信道提出的，但信道极化现象却是普遍存在的，基于前面提到的理论方法对高斯信道中的极化码进行仿真分析，采用BPSK调制，调制之后变为双极性的信号然后再传送至信道，选用加性高斯白噪声。在高斯信道中，需考虑参数信噪比SNR，其为高斯信道重要的衡量指标。

4.3.1 不同信噪比下

图13为误码率在信噪比变化时的变化曲线，此时码长N=1 024，由图可知，随着信噪比的增大，误码率变小。

在高斯信道中，信噪比越大则信道条件越好，出错的概率越小，类似于BEC中的删除概率。信噪比越大说明原始信道的条件越好，而高斯信道的极化依赖于信噪比，所以信噪比越大，极化效果件也越好，即巴氏参数Z的值越小。所以当码长N和码率R一定时，选择用来传输信息的子信道个数也就确定了，此时Z的大小就决定了选择信道的质量好坏。因此信噪比越大，信道的方差越小，极化信道参数Z越小，极化码性能越好，误码率越小。

4.3.2 不同码率条件下

极化码是一种依赖于信道的信道编码，所以信道确定时，信道极化的参数便随之确定，此时码率便是一个影响误码性能的变量。图14为误码率在码率变化时的变化曲线，此时码长N=1 024。

图14 当N=1 024时BER变化曲线Fig.14 BER change curve when N=1 024

由图14可知，随着码率R的减小，误码率也随之变小。由于信道极化的参数已经确定，选择其中的信道都是好的信道。但当R增大时，选择传输信息的信道也会增多，这时不太好的信道会加入进来，造成误码率的增大。

4.3.3 不同码长条件下

码长的值对信道极化现象有很重要的影响，从而影响误码性能。图15为误码率在码长变化时的变化曲线，此时码率R=0.3，由图可知，随着码长N的增大，误码率明显变小。这与BEC信道中的情况类似，当N值增大时，极化的效果更加明显，选择用来传输信息的信道巴氏参数Z的值，肯定比N值小时选出的信道Z值小，所以误码率减小。此外，不同的码长N下，误码率随信噪比的增大差距逐渐变大。

图15 当R=0.3时BER变化曲线Fig.15 BER change curve when R=0.3

5 结论

极化码是通信领域对理论探索的一次质的飞跃，是编码领域的里程碑，具有很高的研究价值。本文重点介绍了信道极化的原理和信道极化的现象，对信道极化中信道组合和信道分解两部分进行了详细分析，并且进一步研究了极化码的编译码过程。虽然信道极化是基于二进制对称信道提出的，但是信道极化现象却是普遍存在的，为此讨论了不同信道中极化的计算方法以及编码参数对误码率的影响。作为目前已知的唯一一种能够被严格证明达到香农限的信道编码方法，极化码可以应用到许多领域，后续的研究还可以从很多方面进行改进。