多光谱图像压缩的联合码率分配—码率控制方法

宋 娟，王柯俨，沈沛意，张 亮

(1.西安电子科技大学软件学院，西安710071;2.西安电子科技大学综合业务网国家重点实验室，西安710071)

0 引言

多光谱图像是由光谱成像仪对同一地物在数十个波段上成像获取的同时包含空间信息和光谱信息的三维数据立方体，被广泛应用于资源勘探、目标识别、环境保护等方面。但是多光谱图像数据量非常庞大，需要采用有效的压缩技术以便图像的存储和传输。

多光谱图像具有较强的谱间相关性和空间相关性，目前多光谱图像压缩编码方法主要包括四类:预测编码［1］、变换编码［2－3］、矢量量化［4］以及近年来提出的分布式压缩方法［5－6］，其中谱间变换 +二维编码的方式具有较低的计算复杂度和较高的压缩性能，应用非常广泛。如倪林和宫久路等人提出了用KL(Karhunen-Loeve)变换结合预测方法，对多光谱图像进行无损及近无损压缩［2－3］。对于谱间变换，KL变换的去相关效果是最优的;对于二维变换编码，基于小波变换的JPEG2000［7］在中低码率下性能较高，但在高码率下压缩效果不理想;而基于预测的JPEG-LS［8］则在中高码率下能取得更好的压缩性能。多光谱图像获取非常困难而且应用比较特殊，因此采用JPEG-LS进行中高码率下的压缩是更优的选择。

基于KL变换和JPEG-LS的有损多光谱图像压缩，势必涉及到两个非常关键的问题，即码率分配和码率控制。首先是码率分配，KL变换后各个分量的能量分布不均，低频分量往往包含更多的能量，而高频分量仅仅占据少量的能量。因此需要根据各分量的能量分布重新分配码率，使得整体质量最优。文献［9－10］提出根据各个分量的标准差大小来分配相应的码率，虽然优于平均分配，但仍然导致各个波段的质量忽高忽低，不够稳定，个别波段的重构质量太差，不能满足应用要求。其次是码率控制，在遥感应用中，码率可控是一个非常重要的指标，如果压缩码率超过了存储空间和链路带宽，就会导致数据溢出，产生解码错误。而JPEG-LS只能控制重构图像的失真，不能控制压缩码率，一定程度上限制了它的应用。文献［11］提出的JPEG-LS码率控制方法首先对图像分区，通过已编码区域的实际累积码率和目标码率的偏差，对编码区域的量化步长进行动态调整，但是码率控制不够精确，实际码率在目标码率附近浮动，不能总小于目标码率，仍然会导致数据溢出。Zhang等人提出的基于拉格朗日数乘的码率控制算法［12］控制码率比较准确，但是算法需要数次迭代才能得到最优的量化步长，复杂度太高。

码率分配和码率控制实质是一个问题，都是根据其能量来调整相应的量化步长，使实际总码率达到目标码率，并且整体质量达到最优。因此，本文提出联合码率分配－码率控制方法，通过分析各分量量化步长对波段重构质量的影响，找到使重构波段失真相当时各个分量量化步长的关系，然后统一对各变换分量编码和码率控制，将码率控制和码率分配有效统一起来，克服已有码率分配方法重构质量不稳定的问题;为了更精确的控制码率，本文提出了基于二次迭代调整的JPEG-LS码率控制方法，以非常小的代价达到准确的码率控制，使实际码率在小于目标码率的前提下，尽可能的逼近目标码率，满足图像通信中固定带宽的要求。

1 基于KL变换和码率可控JPEG-LS的多光谱图像压缩方法

本文提出的基于KL变换和码率可控JPEG-LS的多光谱图像压缩算法框图如图1所示。首先对多光谱图像进行谱间KL变换，有效去除多光谱图像的谱间相关性。为了在各种码率下均能取得高效的压缩性能，本文算法同时支持KL变换的浮点和整数变换，在压缩比小于2倍时，对KL变化矩阵进行整数分解，实现整数变换［13］，大于2倍时采用KL浮点变换。将KL变换后的各分量Y送入本文提出的基于联合码率分配－码率控制的JPEG-LS压缩模块。在本文压缩算法中，码率分配和码率控制有效统一起来，根据重构波段失真相当时各分量量化步长的比例关系，将分量数据重新组织在一起，组织后的分量数据YCIL统一送入本文提出的基于二次迭代调整码率控制的JPEG-LS编码中。在编码过程中，对YCIL中各分量的量化步长统一进行调整，使得实际编码码率尽可能接近目标码率，并按照调整的量化步长对数据进行JPEG-LS编码得到码流，这样得到的各波段的量化失真将是相当的。

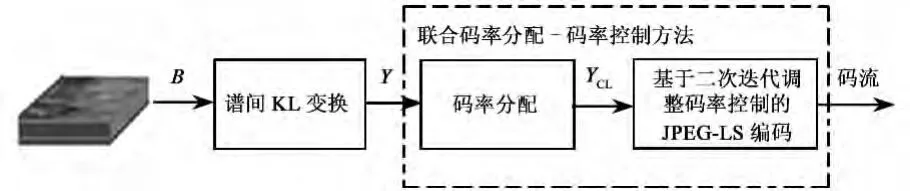
图1 压缩算法框图Fig.1 Diagram of proposed compression algorithm

2 联合码率分配—码率控制方法

多光谱图像经过KL变换得到一系列分量，其中各分量的能量呈递减分布，主分量包含了图像的绝大多数能量，而其余分量仅仅占据了少量的能量。如果给每个分量分配相同的码率，显然不是最优的。因此需要对码率进行分配，使各重构波段的重构质量相当，达到整体性能最优，这正是本文提出码率分配方法的出发点。本文根据JPEG-LS失真可控的特点，首先分析各分量的量化步长对重构波段失真的影响，得到当重构波段失真相当时各分量量化步长的关系。

本文在低倍压缩时采用整数可逆KL变换，变换没有引入失真;在中倍以上压缩采用浮点KL变换，虽然引入精度损失，但和量化失真相比，KL变换引入的失真可以忽略不计。因此根据KL变换公式，直接对KL变换分量{Yi}作反变换，忽略KL变换的失真，即可得到原始多光谱图像{Bi}，如(1)所示，其中AT为变换矩阵A的转置，{mi}为每个波段的均值。

对各分量{Yi}进行量化编码及重构，再进行反变换，即可得到重构波段为公式(2)，其中和分别为重构分量和波段。

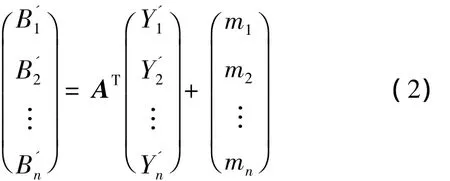
公式(1)和(2)直接相减，即可得到重构波段失真 ΔB={ΔB1，ΔB2，…，ΔBn}和分量失真 ΔY={ΔY1，ΔY2，…，ΔYn}的关系如(3)所示，

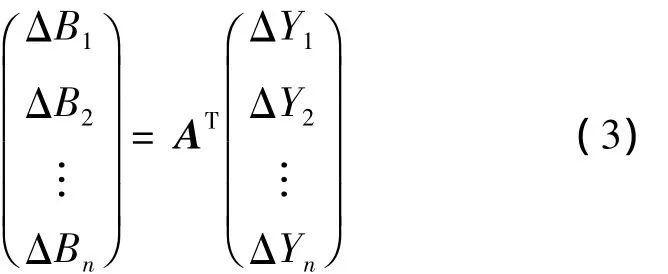
KL变换矩阵AT是正交矩阵，根据矩阵论理论，正交矩阵与向量相乘，只改变向量的角度，而不改变向量的长度，相当于对向量进行旋转，如公式(4)所示

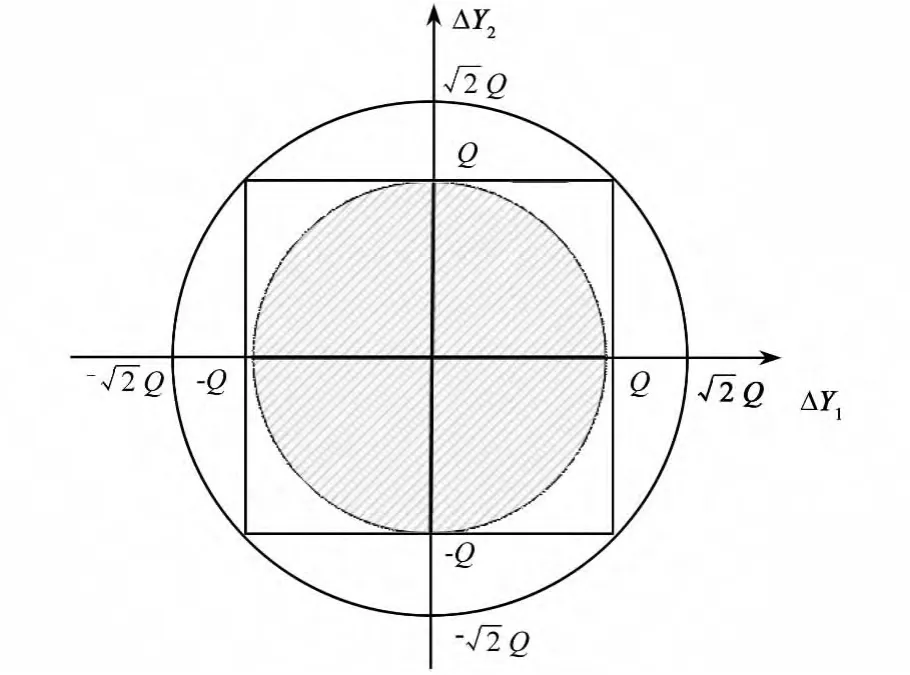
图2 变换前后分量的示意图Fig.2 Component distribution before and after transform

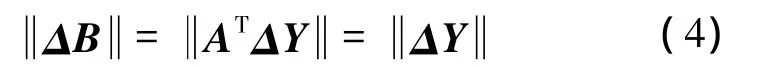
因此AT作用于向量ΔY，相当于对正方形进行旋转，得到ΔB。经过旋转后，对于大多数像素(圆形阴影区域内)而言，ΔB仍然在正方形内，即Bi的失真ΔBi仍然限制在量化步长Q内，而其余少量像素的失真也限制在以内(半径为的圆内)。通过上述分析可以得到以下结论:当各分量都采用相同的量化步长Q时，每个波段内大部分像素的失真都限制在Q以内，极少数失真限制在以内，也就是说各重构波段的失真是相当的。对于更多维数的情况也可以得到类似的结论。

根据以上结论，本文提出了联合码率分配－码率控制方法，将码率分配和码率控制统一起来。首先将各个分量按照CIL(Component-Interleaved-by-Line)的格式拼接在一起，即类似于多光谱图像的数据组织方式BIL(Band-Interleaved-by-Line)，将各分量的数据按行交叉存储直到最后一行，重新存储后的数据记为YCIL，即YCIL的每行数据由每个分量的对应行数据依次拼接构成。将重新组织的分量数据YCIL作为整体送入码率可控JPEG-LS中，在编码过程中，统一进行量化步长调整，使得每行中各个分量的量化步长始终是相等的，以保证得到重构质量相当的重构波段。

3 基于二次迭代调整的码率控制方法

文献［11］提出的码率控制方法首先对图像分区，通过已编码区域的实际累积码率和目标码率的偏差量，对编码区域的量化步长进行动态调整，但码率控制仍然不够精确，实际码率在目标码率附近上下浮动，不能满足固定链路带宽的要求。为了更加精确的控制码率，本文提出了基于二次迭代调整的JPEG-LS码率控制方法，在第一次对整幅数据完成基于行调整的码率控制后，再返回到最后N行对量化步长进行二次迭代调整，使得实际码率在尽可能接近目标码率的前提下，又略小于目标码率，避免码流溢出，以满足图像传输中严格的带宽和存储限制。本文提出的基于二次迭代调整的码率控制算法流程图如图3所示。

经常有准妈妈在新浪微博上问我：宝宝是不是越小越好生？越大越健康？宝宝在妈妈肚子里养得越久是不是生出来就越好养？剖宫产的宝宝会不会更聪明？孕育生命的准妈妈们，即将迎来自己的宝宝，心情激动，但是面对社会上众说纷纭的各种说法，却难以适从。今天我们一起探讨一下与分娩有关的几个话题，纠正几个常见的认识误区。

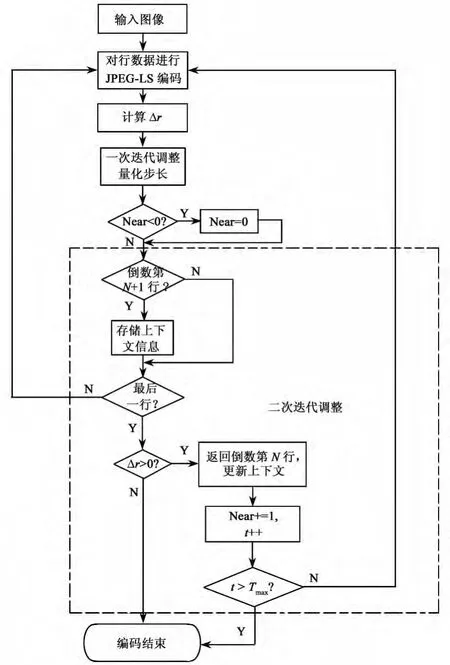
图3 JPEG-LS码率控制流程图Fig.3 The flow chart of rate control in JPEG-LS

(1)设置量化步长Near值的初始值，根据大量的实验得到经验值，当目标压缩比＜4时，Near=0;当目标压缩比≥4时，Near=4;

(2)对当前行编码数据以Near值进行预测量化编码，得到当前累积码率;

(3)一次迭代调整:计算当前累积码率和目标码率的差值Δr，将Δr和预设的码率门限进行比较，如果当前码率大于目标码率，则使Near值增加一个适当的步长step，否则使Near值减小一个适当的步长step，如果Near＜0，令 Near置0。根据大量的实验，本文离线训练出码率差Δr和Near的调整步长step之间的一组对应关系，预设的14个码率控制门限为 {0.5，0.45，0.35，0.30，0.25，0.15，0.05，－0.05，0.13，－ 0.15，－ 0.25，－ 0.39， － 0.46，－0.53}，对应于非零的14个调整步长step={±1，±2，±3，±5，±6，±8，±10};

(4)转至下一行，如果到达倒数第N+1行，则存储当前行的上下文信息，以便对图像的最后N行重新编码，进行码率的二次迭代调整;

(5)判断是否为最后一行，如果否，则转至步骤(2)进行一次迭代调整，如果是，则转至步骤(6)进行二次迭代调整;

(6)退回至倒数第N行，进行二次迭代调整:判断Δr是否大于0(即实际码率是否大于目标码率)，以进一步调整码率。如果Δr＜0，则说明实际码率小于目标码率，满足码率要求，编码结束;如果Δr＞0，则不满足码率要求，退回至倒数第N行重新编解码调整，Near加1，迭代次数t计数;

(7)如果t≤Tmax，则转至步骤(2)重新调整Near值;否则退出后N行的码率调整迭代，编码结束。

由于本文提出的码率控制方法根据已编码数据的累积码率和目标码率之差调整每一行的Near值，而这些信息在解码端是已知的，解码端通过相同的步骤即可以得到完全相同的Near调整值，因此并不需要将Near的调整值传递至解码端。

4 实验结果与分析

4. 1 码率控制

图4 IKONOS测试图像Fig.4 Multispectral images from IKONOS

由于本文压缩方法是基于二次迭代调整的JPEG-LS码率控制方法，所以本文首先对2种码率控制算法进行评估，分别是文献［11］提出的基于分区一次调整的码率控制方法以及本文算法(二次迭代调整)。图5分别为这2种方法以3倍独立压缩多光谱图像各波段时的码率(bpp)和重构图像峰值信噪比(PSNR)值。

从图5可以看出，和分区一次调整方法相比，本文提出的基于二次迭代调整的码率控制方法控制码率更加精确，在实际码率低于目标码率的前提下，非常逼近目标码率，和目标码率的偏差仅仅为0.006 4;而且由于码率控制更加准确，重构质量也明显优于分区一次调整，平均PSNR比分区一次调整提高了大约1dB。

本文方法仅仅对少数行进行了简单的二次迭代调整，因此并没有增加太多编码复杂度，如表1所示，编码运行时间仅仅比分区一次调整方法增加了大约10ms。

表1 编码时间比较Table 1 Comparison of encoding time

4. 2 码率分配

图5 码率控制比较Fig.5 Comparison of Rate control scheme

为了评估码率分配方法的性能，本节选用了3种算法，一种是基于二次迭代调整的码率可控JPEG-LS独立压缩算法，另外两种是基于KL变换和码率可控JPEG-LS的联合压缩算法，其中一种采用了文献［10］提出的基于标准差的码率分配方法，另一种是本文提出的联合码率分配－码率控制算法。为了评估不同方法的整体性能和重构质量稳定性，本节采用每组多光谱图像的PSNR平均值和PSNR标准差作为评价指标。

图6显示了这3种算法在2、3倍压缩比下每组多光谱图像的PSNR平均值和标准差(为了便于统计，无损时PSNR记为100dB)。从图中可以看出，基于KL变换的谱间联合压缩方法由于利用了谱间相关性，压缩性能基本上优于各波段独立压缩方法，但基于标准差的码率分配方法不是最优的，导致在2倍压缩时压缩性能反而不如独立压缩，可见码率分配对系统的率失真性能影响之大。

如图6所示，本文提出的联合码率分配－码率控制方法整体性能最优，每组多光谱图像的平均PSNR均优于独立压缩和基于标准差的码率分配方法。如图6(a)所示，本文算法在2倍压缩时有3组多光谱图像达到了无损压缩。对于重构质量的稳定性，独立压缩均匀分配码率导致各个波段重构质量波动极大，PSNR的标准差最大，稳定性最差;基于标准差的码率分配方法根据波段的标准差对码率重新分配，稳定性较高;而本文算法对各个分量统一调整量化步长，各个波段的重构质量最稳定，各个波段PSNR的标准差保持在0.1以内。

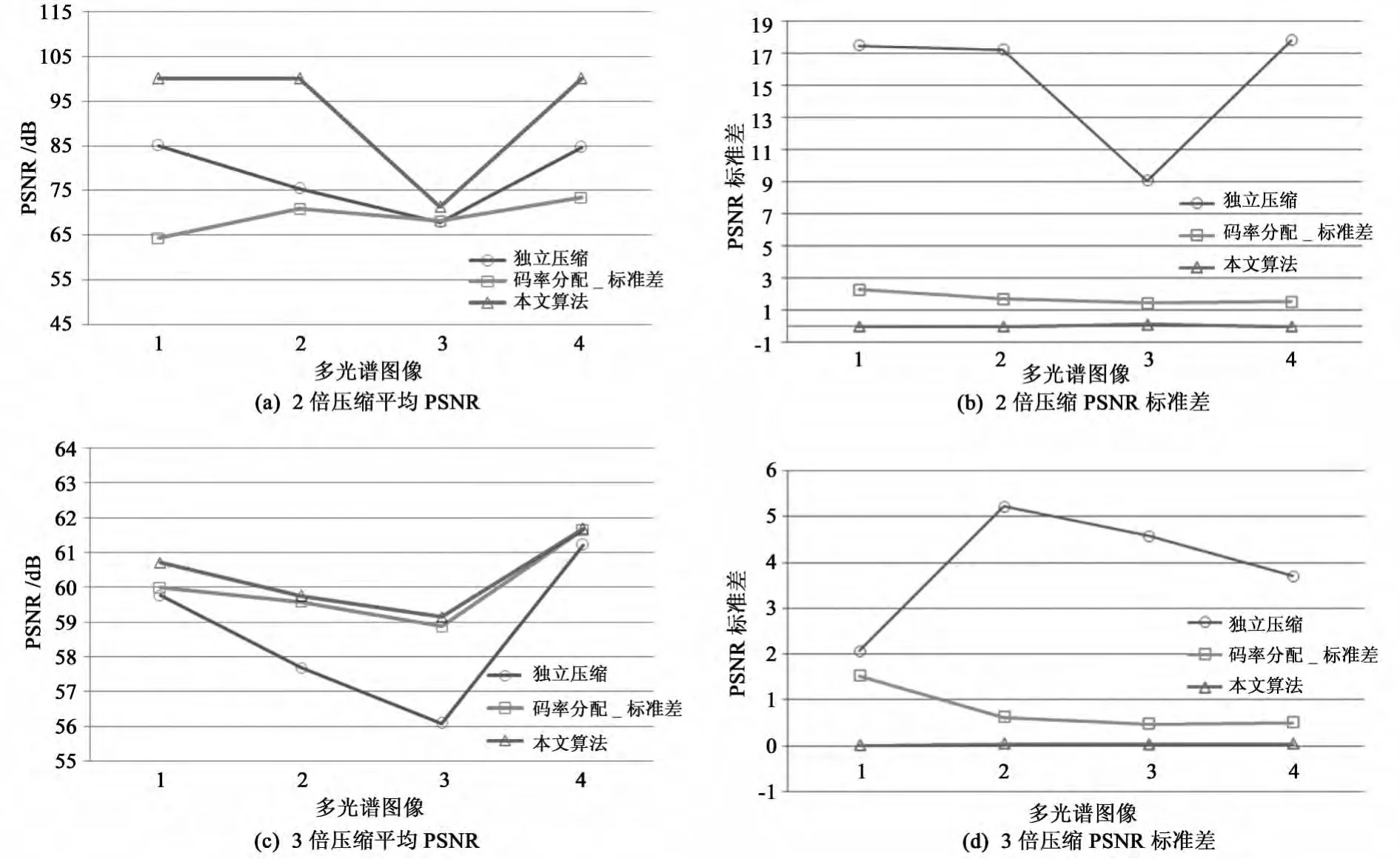
图6 码率分配压缩性能比较Fig.6 Performance comparison of rate allocation scheme

5 结论

本文针对基于KL变换和JPEG-LS编码的多光谱图像压缩系统中码率控制不准确以及码率分配效果差的问题，提出了一种联合码率分配－码率控制方法。通过分析重构波段失真相当时KL变换各分量量化步长的关系，本文对各分量数据重新组织统一控制码率，将码率分配和码率控制有效统一起来。为了更精确的控制码率，本文还提出了基于二次迭代调整的码率控制方法，在对整幅图像数据完成基于行的量化步长调整后，对最后N行数据重新迭代调整量化步长，使得实际码率在小于目标码率的前提下尽可能的接近目标码率。实验结果表明本文算法控制码率非常精确，而且具有较低的计算复杂度;本文算法的整体重构质量也明显优于其它码率分配方法，而且各波段重构质量非常稳定。

［1］ Mielikainen J，Huang B.Lossless compression of hyperspectral images using clustered linear prediction with adaptive prediction length［J］.IEEE Signal Processing Letters，2012，9(6):1118－1121.

［2］ 倪林.基于分类K-L变换的多波段遥感图像近无损压缩方法［J］.遥感学报，2001，5(3):205 －213.［Ni Lin.Near-lossless compression of multispectral remote sensing image based on classified K-L transform［J］.Journal of Remote Sensing，2011，5(3):205 －213.］

［3］ 宫久路，谌德荣，曹旭平，等.一种最大压缩误差可控的高光谱图像压缩算法［J］.宇航学报，2009，30(6):2303 －2307.［Gong Jiu-lu， Chen De-rong， Cao Xu-ping， et al. A Hyperspectral image compression algorithm of maximum compression error controllable［J］.Journal of Astronautics，2009，30(6):2303 －2307.］

［4］ Chen Y，Zhang Y，Zhang Y，et al.Fast vector quantization algorithm for hyperspectral image compression［C］.IEEE Data Compression Conference，Snowbird，USA，Mar 29 －31，2011.

［5］ 粘永健，万建伟，何密，等.基于分布式信源编码的高光谱图像无损压缩研究进展［J］.宇航学报，2012，33(7):860 －869.［Nian Yong-jian，Wan Jian-wei，He Mi，et al.Research progress of lossless compression for hyperspectral image using distributed source coding［J］.Journal of Astronautics，2012，33(7):860 －869.］

［6］ 孔繁锵，吴宪云.基于分布式信源编码和感兴趣区域编码的干涉多光谱图像压缩［J］.宇航学报，2011，32(2):367 －373.［Kong Fan-qiang，Wu Xian-yun.An improved distributed source coding and ROIcoding based interferometric multi-spectral image compression algorithm［J］.Journal of Astronautics，2011，32(2):367 －373.］

［7］ Skodras A，Christopoulos C，Ebrahimi T.The JPEG2000 still image compression standard［J］. IEEE Signal Processing Magazine，2001，18(5):36－58.

［8］ Weinberger M J，Seroussi G，Sapiro G.LOCO-I lossless image compression algorithm:principles and standardization into JPEGLS［J］.IEEE Transactions on Image Processing，2000，l9(8):1309－1324.

［9］ Lucero A，Cabrera S，Aguirre A，et al.Comparison of bit allocation methods for compressing three-dimensional meteorological data after applying KLT［C］.IEEE International Symposium of Geoscience and Remote Sensing，Alaska，USA，Sep.，20 －24，2004.

［10］ 孙蕾，罗建书，谷德峰.基于谱间预测和码流预分配的高光谱图像压缩算法［J］.光学精密工程，2008，16(4):752 －757.［Sun Lei，Luo Jian-shu，Gu De-feng.Hyperspectral image compression algorithm based on prediction between bands and rate pre-allocation［J］.Optics and Precision Engineering，2008，16(4):752 －757.］

［11］ Edirisinghe E A，Bedi S.Variation of JPEG-LS to low cost rate control and its application in region-of-interest based coding［J］.Signal Processing:Image Communication，2003，18(5):357 －372.

［12］ Zhang J，Li Y S，Liu K，et al.The rate control scheme for JPEG-LS with high bitrate［C］. SPIE， Satellite Data Compression，Communications， and Processing， San Diego，USA，Aug.11 －16，2012.

［13］ Hao P，Shi Q.Reversible integer KLT for progressive-to-lossless compression of multiple component images［C］.IEEE Int.Conf.Image Process，Barcelona，Spain，Sep.，14 －17，2003.