构造长度为4ps的量子重根循环码
2023-10-31汪余婷
汪余婷, 刘 丽
(合肥工业大学 数学学院,安徽 合肥 230601)
0 引 言
自文献[1]和文献[2]提出量子纠错码以来,量子码的相关研究开始受到关注。量子纠错是量子计算和量子通信得以实现的重要保证,是信息科学的一个重要组成部分;循环码作为经典纠错码中的重要环节,在量子纠错方面具有重要作用。本文主要研究的是Fq上码长为4ps的重根循环码,并利用它们构造量子码。

本文基于Steane扩展构造,给出Fq上线性码C为自正交码的条件,构造几类参数较好的非二元量子码。根据在Fq上码长为4ps的重根循环码的最小汉明距离以及对偶包含的关系,确定自正交码的条件;根据Steane扩展构造的相关内容,构造几类参数较好的量子码。
1 基础知识
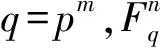
众所周知,Fq[x]/〈xn-1〉的任一个理想都是主理想,即C=〈g(x)〉,其中g(x)是首一的且满足g(x)|(xn-1),被称为生成多项式。码C的对偶定义为:

长度为n维数为k的q进制量子码是希尔伯特空间H=Cqn=Cq⊗…⊗Cq的子空间。设|x>是Cq的正交基且x、a、b∈Fq。在Cq上,定义X(a)|x>=|x+a>和Z(b)|x>=ωtr(bx)×|x>,其中tr是从Fpm到Fp的迹映射,且ω=exp(2πi/p)是p次本原单位根。

X1(a)=X1(a1)⊗X1(a2)⊗…⊗X1(an),
X2(a)=X2(a1)⊗X2(a2)⊗…⊗X2(an),

若C是[[n,k,d]]q量子码,则k≤n-2d+2,称该界为量子Singleton界;若量子码C的参数满足k=n-2d+2,则称C为量子最大距离可分(maximum distance separable,MDS)码。
2 长度为4ps重根循环码的汉明距离
设C是Fq上码长为4ps的循环码,则C是环R=Fq[x]/〈x4ps-1〉的一个理想。


下面给出Fq上码长为4ps的循环码包含其对偶码的充要条件。


结合文献[26]给出的Fpm上码长为4ps的最小汉明距离,对偶包含码的汉明距离见表1~表3所列。

表1 对偶包含码Ci,j,k的汉明距离
3 构造量子码
本节根据长度为4ps的重根循环码构造几类量子码。

定理2 设q是奇素数p的幂次,若s≥2或p≥5且s=1,则存在一个参数为[[4ps,4ps-ps-1-4,3]]q的量子码。
证明考虑Fq上码长为4ps的循环码
Ci,j,k=〈(x-1)i(x+1)j(x2+1)k〉,
其中:i=ps-1+1;j=0且k=1。
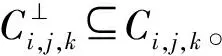
例1设q=p≥5且s=1,则存在一个p元参数为[[4p,4p-5,3]]q的量子码。由量子Singleton界可知,这是一个码长为4p且最小距离为3的q元量子码,其维数是4p-4。经验证,这是一个参数较好的量子码。
定理3设q是奇素数p的幂次,若s≥2或p≥7且s=1,则存在一个参数为[[4ps,4ps-3ps-1-6,4]]q的量子码。
证明考虑Fq上码长为4ps的循环码
Ci,j,k=〈(x-1)i(x+1)j(x2+1)k〉,
其中:i=2ps-1+1;j=0且k=1。
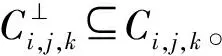
例2 设q=p≥7且s=1,则存在一个p元参数为[[4p,4p-9,4]]q的量子码。由量子Singleton界可知,这是一个码长为4p且最小距离为4的q元量子码,其维数是4p-8,是一个参数较好的量子码。
定理4 设q是奇素数p的幂次,且q≡1(mod 4),若s≥2或p≥5且s=1,则存在一个参数为[[4ps,4ps-ps-1-3,3]]q的量子码。
证明考虑Fq上码长为4ps的循环码
Ci,j,k,l=〈(x-1)i(x+1)j(x-δ)k(x+δ)l〉,
其中:δ2=-1;i=ps-1+1;j=l=0且k=1。
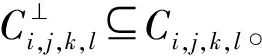
例3设q=p≥5且s=1,则存在一个p元参数为[[4p,4p-4,3]]q的量子码。由量子Singleton界可知,这是一个码长为4p且最小距离为3的q元量子码,其维数是4p-3,是一个参数较好的量子码。
定理5 设q是奇素数p的幂次,且q≡1(mod 4),若s≥2或p≥7且s=1,则存在一个参数为[[4ps,4ps-3ps-1-5,4]]q的量子码。
证明考虑Fq上码长为4ps的循环码
Ci,j,k,l=〈(x-1)i(x+1)j(x-δ)k(x+δ)l〉,
其中:δ2=-1;i=2ps-1+1;j=k=1且l=0。
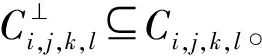

表2 0≤l≤j≤k≤i≤ps时对偶包含码Ci,j,k,l的汉明距离
例4设q=p≥7且s=1,则存在一个p元参数为[[4p,4p-8,4]]q的量子码。由量子Singleton界可知,这是一个码长为4p且维数是4p-8,其最小距离最大为5的q元量子码,因此是一个近似MDS码。
定理6 设q是奇素数p的幂次,且q≡1(mod 4),若s≥2或p≥7且s=1,则存在一个参数[[4ps,4ps-ps-1-6,3]]q的量子码。
证明考虑Fq上码长为4ps的循环码
Ci,j,k,l=〈(x-1)i(x+1)j(x-δ)k(x+δ)l〉,
其中:δ2=-1;i=2ps-1+1;j=k=1且l=0。
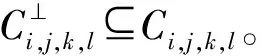

表3 0≤l≤k≤j≤i≤ps时对偶包含码Ci,j,k,l的汉明距离
例5 设q=p≥7且s=1,则存在一个p元参数为[[4p,4p-8,3]]q的量子码。由量子Singleton界可知,这是一个码长为4p且维数是4p-8的q元量子码,其最小距离最大为5的q元量子码,因此是一个近似MDS码。
5 结 论
本文在Fq上码长为4ps重根循环码的基础上,基于Steane扩展构造,构造了几类极小距离、维数等参数均有改进的非二元量子码。利用循环码的其他码长来构造新的参数较好的量子码是进一步可以研究的问题。
