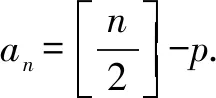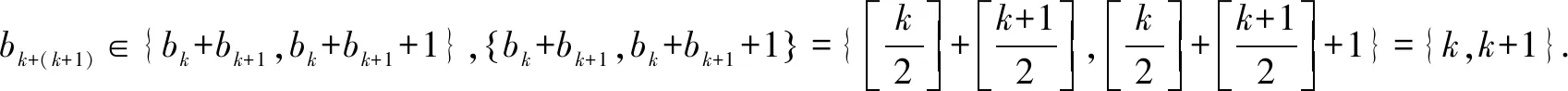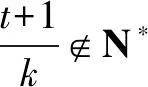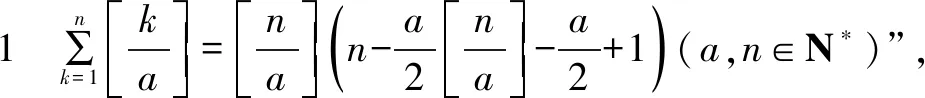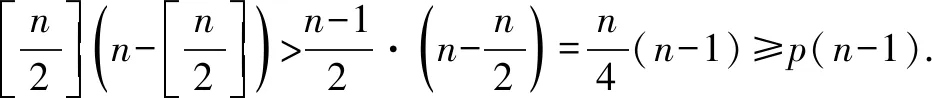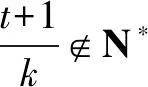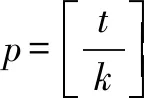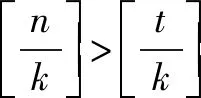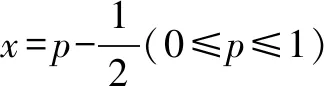对2021年高考数学北京卷压轴题结论的推广

2021-11-24甘志国

数理化解题研究 2021年31期

关键词：中令归纳法正整数

甘志国

(北京丰台二中 100071)

题目对于已知的实数p，定义同时满足下列三个条件的数列{an}叫做RP数列：

1.a1+p≥0，a2+p=0；

2.∀n∈N*，a4n-1

3.∀m,n∈N*,am+n∈{am+an+p,am+an+p+1}.

(1)判断前4项分别为2,-2,0,1的数列可能是R2数列吗？并说明理由；

(2)若{an}是R0数列，求a5的值；

(3)是否存在实数p，使得存在RP数列{an}(其前n项和是Sn)，满足∀n∈N*,Sn≥S10？若存在，请求出所有这样的p；若不存在，请说明理由.

定理1 若p是已知的实数，则同时满足下列三个条件：

(1)a1=-p,a3=1-p；

(2)∀n∈N*,a2n-1

证明设bn=an+p(n∈N*)，可得数列{bn}同时满足下列三个条件：

(1)b1=0,b3=1；

(2)∀n∈N*，b2n-1

(3)∀m,n∈N,bm+n∈{bm+bn,bm+bn+1}.

由(3)可得b2∈{2b1,2b1+1}，再由(1)可得b2∈{0,1}，又由(1)(2)可得b2=1.

还可得：b4∈{b1+b3,b1+b3+1},b4∈{1,2}，再由1=b3

下面对n用第二数学归纳法证明b2n-1=n-1,b2n=n(n∈N*).

由前面的论述可得n=1,2,3时均成立.

定理2 若p是已知的实数，则同时满足下列三个条件：

(1)a1=a2=-p；

(2)∀n∈N*,a3n-1

证明设bn=an+p(n∈N*)，可得数列{bn}同时满足下列三个条件：

(1)b1=b2=0；

(2)∀n∈N*,b3n-1

(3)∀m,n∈N,bm+n∈{bm+bn,bm+bn+1}.

由(3)可得b3∈{b1+b2,b1+b2+1}，再由(1)可得b3∈{0,1}，又由(1)(2)可得b3=1.

下面对n用数学归纳法证明b3n+1=b3n+2=n,b3n+3=n+1(n∈N).

(1)由前面的论述可得n=0时成立.

(2)假设n=t(t∈N)时成立：b3t+1=b3t+2=t,b3t+3=t+1.则b3t+4∈{b3t+2+b2,b3t+2+b2+1},b3t+4∈{t,t+1};b3t+4∈{b3t+3+b1,b3t+3+b1+1},b3t+4∈{t+1,t+2}，所以b3t+4=t+1.

还可得b3t+5∈{b3t+3+b2,b3t+3+b2+1},b3t+5∈{t+1,t+2};b3t+6∈{b3t+4+b2,b3t+4+b2+1},b3t+6∈{t+1,t+2}.再由(ⅱ)可得b3t+5

定理3 若k(k≥4)是已知的正整数，则同时满足下列三个条件：

(1)bi≥0(i=0,1,2,…,k-3),bk-2=0；

(2)∀n∈N*，bkn-1

证明当j=0,1,2,…,k-2时，由(3)可得bj+(k-j-2)∈{bj+bk-j-2,bj+bk-j-2+1}.由(1)可得bj+(k-j-2)=bk-2=0,bj+bk-j-2+1≥1，所以bj+bk-j-2=0.再由(1)可得bj=0(j=0,1,2,…,k-2).

由(3)可得bn+1∈{bn+b1,bn+b1+1},bn+2∈{bn+b2,bn+b2+1}.再由b1=b2=0，可得bn+1,bn+2∈{bn,bn+1}，所以bkn-1,bkn∈{bkn-2,bkn-2+1}(n∈N*).再由(2)，可得bkn-1=bkn-2,bkn=bkn-2+1(n∈N*).

①

在①中令n=1，可得bk-1=bk-2=0,bk=bk-2+1=1.

(1)由前面的论述可得n=0时成立.

(2)假设n=0,1,2,…,t时均成立.

当j=0,1,2,…,k-2时，由(3)可得：

bk(t+1)+j=b[k(t-1)+k-1]+[k+(j+1)],bk(t+1)+j∈{bk(t-1)+k-1+bk+(j+1),bk(t-1)+k-1+bk+(j+1)+1}.再由归纳假设中的n=t-1,1时均成立，可得bk(t+1)+j∈{t,t+1}.

bk(t+1)+j=bkt+(k+j),bk(t+1)+j∈{bkt+bk+j,bkt+bk+j+1}.再由归纳假设中的n=t,1时均成立，可得bk(t+1)+j∈{t+1,t+2}.所以当j=0,1,2,…,k-2时，bk(t+1)+j∈{t,t+1}∩{t+1,t+2},bk(t+1)+j=t+1.再由①中的第一个等式，可得bk(t+1)+k-1=bk(t+1)+k-2=t+1.所以n=t+1时成立，因而欲证结论成立.