直线与双曲线渐近线交点的一个性质及应用
2021-11-22广东省广州市广东仲元中学511400邓胜旺
中学数学研究(广东) 2021年20期
广东省广州市广东仲元中学(511400) 邓胜旺
近期在研究双曲线与直线的问题中发现一个有趣的性质.
1 性质及证明

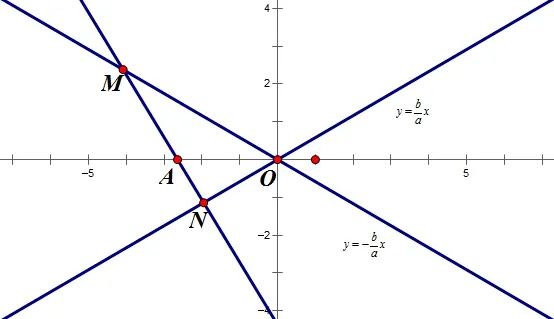
图1


①式可以进一步表述为与离心率相关的式子
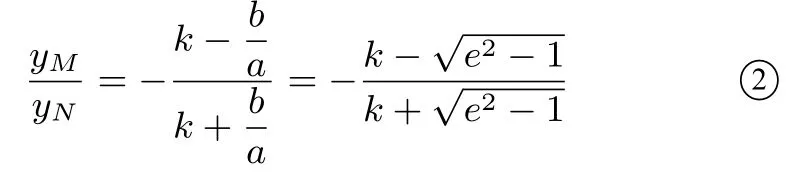
在证明过程中,点A(x0,0)在两个纵坐标作比的过程中约掉了,即x0可以是x轴上除原点之外任意一点,由此可以有多个特殊的应用.
2 性质在命题与解题中的应用
2.1 直线过顶点


2.2 直线过焦点


2.3 定点变式

分析本题是一道界定不明确,问题的构成存在未知[1]的结构不良试题.表现在A和B两点的位置不明确,必须加以分类讨论.常规解法入口宽但运算量较大,难度为高考压轴题或高中数学联赛初赛题.


3 性质的拓展
3.1 双曲线系

3.2 椭圆的“虚渐近线”

3.3 抛物线中特殊定点
对于任意抛物线C:y2= 2px, 过其上的两点M(x1,y1),N(x2,y2) 的直线与x轴交于点G(t,0), 则必有y1·y2=−2pt恒成立.

综上可得y1y2=−2pt.
