基于波利亚“怎样解题”表的数学问题探究*——以一道初中平面几何题为例

广东省广州市增城区应元学校(511399) 郑育玲

1 引言

波利亚“怎样解题”表集中体现其探索法与元认知思想,在函数、方程、立体几何、解析几何等方面的解题教学中应用广泛.波利亚曾说:“变化问题使我们引进了新的内容,从而产生了新的接触,产生了和我们问题相关的元素接触的新的可能性.”[1]“怎样解题”表的四个阶段“弄清问题、拟定计划、实施计划、回顾”就是对数学问题探究和解决的一个监控过程.下面将结合一道例题来对数学问题探究进行详细叙述.

2 基于波利亚“怎样解题”表的数学问题探究

2.1 题目呈现

如图所示,在ΔABC中,∠CAB是钝角,AB=BD=DC,∠BCA=30°,求∠CAD的大小.

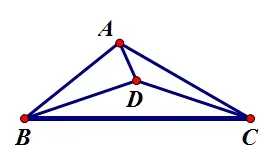
图1

思路分析: 本题是一道初二年级的平面几何题目,考查学生对平面几何知识的综合运用能力.题目当中涉及的知识点有等腰三角形的性质、全等三角形的判定以及直角三角形的性质.从题目的已知条件出发,学生很容易直接从三角形的内角和180°出发,利用等腰三角形底角相等的性质来建立等量关系式,而此方法将没办法进行到底.因此,这个时候就需要转变思维,由边相等联想到利用等腰三角形“三线合一”的性质,添加辅助线.可此时又将遇到一个难题,条件“是钝角”将作何用呢? 这是学生解决这一问题的难点.

2.2 基于波利亚“怎样解题”表的数学问题探究

下面,将结合波利亚“怎样解题”表的提示语指导学生进行解答:

(1)弄清问题,确定已知未知

盯住目标! 题目要求我们做什么? 条件是什么?

要求∠CAD的大小.已知条件有三个: ①边的等量关系AB=BD=DC, ②已知角的度数∠BCA= 30°,③∠CAB是一个钝角.

从已知条件中,你能想到与之相关的知识点有哪些?

三角形内角和为180°;等腰三角形的底角相等和“三线合一”的性质;在直角三角形中,30°的角所对的边等于斜边长的一半.

(2)拟定计划,探究数学问题

上述相关知识点中,哪一个可以帮助你解决目标? ——试试从三角形内角和为180°进行解决,引入符号标记各角如图所示.

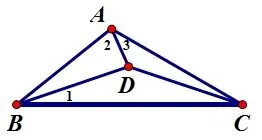
图2

你将选择哪个三角形利用内角和求解? ——ΔABC中,∠ABC+∠ACB+∠BAC=180°.

现在还差哪个角需要表示出来? ——∠ABC.由等腰三角形底角相等可以得到∠ADB= ∠2, 则ΔABD中∠ABD=180°−2∠2,因此∠ABC=180°−2∠2+∠1.在ΔABC中利用内角和为180°整理得到关于∠1、∠2 和∠3的等量关系式为: ∠2−∠1−∠3=30°.

显然只有一个方程是不能将三个未知量求解出来的,你还能构造出其他的等量关系吗? ——不能.

接下来,怎么办? 你还可以利用什么条件? 回到相关知识点中看看? ——等腰三角形“三线合一”!

你是否需要添加辅助线? ——过点D作线段BC的垂线,如图所示,交BC于点E,交AC于点M.

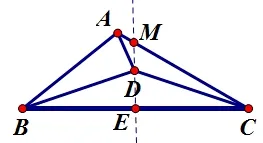
图3

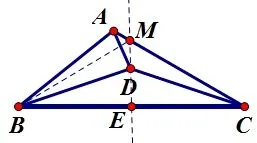
图4

由此你能得到哪些条件? ——∠MEC= ∠MEB=90°,∠EMC=60°.

点M在哪条线上? ——BC的中垂线上.

接下来怎么办? 目标解决了吗? ——证明ΔABMΔDBM.

要证明全等,根据现有条件,选择什么证明方法? ——边边边,现在已知AB=DB,还有一条公共边BM,因此只需要再得到AM=DM的条件就可以了.

纵观题目,你还有哪个条件没有用上? ——∠CAB为钝角.

钝角有什么性质? ——作它的一条高, 垂足一定在ΔABC的外部.

试试看! ——过点B作BF垂直于CA,如图5 所示.

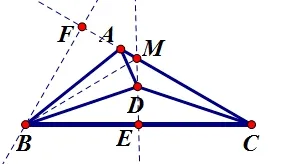
图5

放在ΔBCF上看看,你能得到什么线段之间的长度关系吗? ——在直角三角形中,30°角所对的边是斜边的一半!因此=BE.

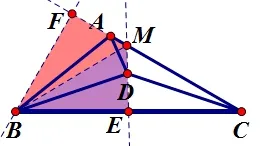
图6

接下来怎么办? ——可以证明ΔFBMΔEBM(HL)了.

你能得到什么有用的条件? ——MF=ME.

离目标越来越近了, 还差什么? ——若还能知道AF=DE,就能证明MA=MD了.

它们有什么共同的特征? ——都是直角三角形中的一条直角边,斜边对应相等.

另一直角边呢? 是什么关系? ——也对应相等!

那你有什么解决的办法? ——ΔFBAΔEBD(HL).

可以证明MA=MD了吗? ——可以了,由MF=ME,且AF=DE,两式对应相减即可得到MA=MD.

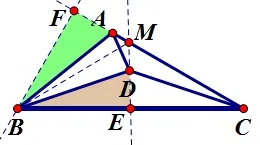
图7

那∠CAD的度数呢? ——在ΔMAD中, ∠AMD=120°,且MA=MD,因而∠CAD=30°.

(3)执行计划,落实解题步骤

现在可以把你的解题计划付诸实施了,你能清楚地看出每一步骤是正确的吗? 落实与检查每一步骤.

(4)回顾反思,构建知识迁移

你能检验你的结果吗? 如果改变了条件,你会解决这个问题的变式吗?

变式1: 将条件“∠CAB为钝角”改为“∠CAB为锐角”,其他条件不变.

如图9 所示,在ΔABC中,∠CAB为锐角,AB=BD=DC,∠BCA=30°,求∠CAD的度数.

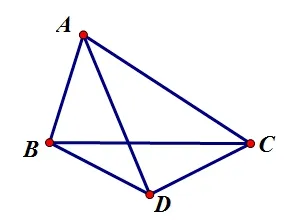
图9

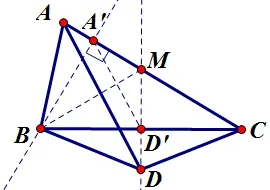
图10

思路: 作辅助线的方法与上述问题相同,先是过点D作BC的垂线,再过点B作AC的垂线,连接BM.接下来只需证明两次三角形全等,问题就迎刃而解了,最终求得∠CAD仍然等于30°.

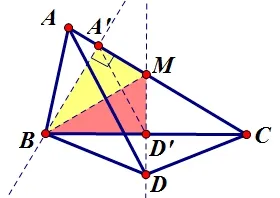
图11

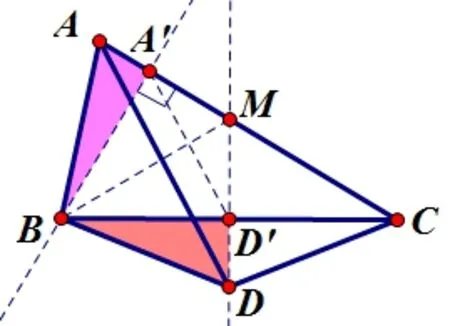
图12

变式2: 在基于原题目的条件下,将“点D在ΔABC内部”改为“∠BCD >30°”,其他条件不变.

如图所示,在ΔABC中,∠CAB是钝角,AB=BD=DC,∠BCA=30°,且∠BCD >30°,求∠CAD的度数.

图13

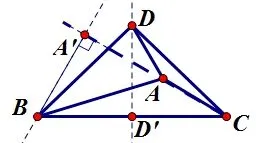
图14

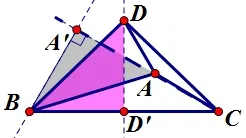
图15

思路: 作辅助线方法与上述类似, 再通过证明ΔA′BAΔD′BD,此问题也将迎刃而解.

你还能想到其他的变式吗? 并尝试将其求解出来.

3 结语

在解题过程中,注重培养反思意识和反思行为,实质上就是数学问题探究能力的培养.解题后的“回顾与反思”这一步骤,不仅仅提供找到一个更优美或更简单的可能性,它还能让学生体验到如何提出问题,体验到真正“做数学”的味道[4].同样地,对于一个教师而言,在问题解决的过程中,最为重要的组成部分是尽力去创造出相似或者相关的问题,从而帮助学生培养数学问题探究的能力.本文结合了波利亚的怎样解题思想来叙述中学数学问题探究,利用典型例子对问题多次表征,通过回顾反思,实现知识的正迁移.