新高考模式下有效教学的思考与探究——“懂而不会现象”的思考

广东省广州市番禺区石碁中学(511450) 张洁婕

1 “懂而不会的现象”案列分析

1.1 存在问题: 基础知识薄弱

教学片段1.若x >0,求f(x) = 4x+的最小值;(2)若x<0,求f(x)=4x+的最大值.

学生做法: 直接利用基本不等式,求得(1)(2)结果相同.

分析: 未考虑基本不等式的前提条件,忽略一正的条件.

1.2 存在问题: 数学思维障碍

教学片段2: 已知{an}是各项均为正数的等比数列,{bn}是等差数列,且a1=b1=1,b2+b3=2a3,a5−3b2=7.

(I)求{an}和{bn}的通项公式;

(Ⅱ)设cn=anbn,n ∈N∗,求数列{cn}的前n项和.

学生做法: (1).对于本题的第二问,空白;(2)第一步Sn,第二步3Sn,2Sn;(3)只列到qSn,之后就不写了.

分析: (1)对于本题的第二问, 有些同学完全没有思路,无从下手;(2)有些同学知道用错位相减,但不会选q;(3)有些同学知道方法(只列到qSn),之后就不会求解.学生想不到错位相减的方法或不知道如何乘以q.

教学片段3: 已知定义域为R 的函数是奇函数:f(x) =

(1)求实数a,b的值;(2)判断并证明f(x)在(−∞,+∞)上的单调性;(3)若对任意实数t ∈R,不等式f(kt2−kt)+f(2−kt)<0 恒成立,求k的取值范围.

学生做法: 在做第三问时,很多同学不会转化,无从下手.

分析: 未分类讨论、未数形结合(懒得动笔),未养成分类的思维,思维单一固定化.

1.3 存在问题: 迁移应用能力受阻

教学片段4:【2020 全国1 文3】.如图,将钢琴上的12个键依次记为a1,a2,··· ,a12.设1 ≤i < j < k≤12.若k–j= 3 且j–i= 4, 则称ai,aj,ak为原位大三和弦; 若k–j=4 且j–i=3,则称ai,aj,ak为原位小三和弦.用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为( )

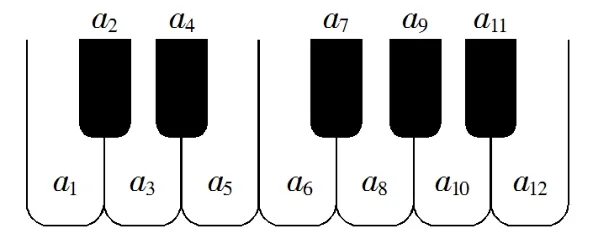
A.5 B.8 C.10 D.15

学生做法: 无从下手,读不懂题意.

分析: 不会提取关键信息、不会转化成数学问题

针对上述问题并进行有关分析,归纳出如下几个原因:

原因1: 概念不清,忽略条件,不理解条件、概念;

原因2: 机械记忆公式,而不理解公式推导过程;

原因3: 思维固化、未形成数形结合的习惯和思维,函数的数学思想未形成;

原因4: 数学建模、统计思想较为薄弱.

基于上述原因,在新高考模式下,教师面临更大的挑战.

2 新高考模式下有效教学的思考与探究

2.1 注重基础知识

针对教学片段1 中不等式的题目,条件不一样,得到的结果不一样,第二小问中,要想把x <0 转化成基本不等式“一正”的条件,只需−x >0 即可.在新高考模式下,对学生基础题目的考察越来越多.同样的基础题目,在高考卷中也有很多.因此教师在教学中要注重基础题目,巩固基础练习,使学生理解并会应用.

例1(2018 天津文)(1)已知a,b ∈R,且a −3b+6=0,则的最小值为____.

(2)数列{an}中a1= 2,an+1= 2an,Sn为{an}的前n项和,若Sn=126,则n=____.

分析(1)由题意首先求得a −3b的值,然后结合均值不等式的结论整理计算即可求得最终结果,注意等号成立的条件.在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.

(2)等比数列的概念及等比数列求和.

2.2 注重数学思维

2.2.1 定理公式推导过程

针对教学片段2 的数列问题,很多同学只是机械的记忆“错位相减”,并不知道为何会有这种方法,以及这个方法为何适用于“差比数列”.实际上,在课本必修5 课本p55,证明等比数列前n项和的时候,就用到了“错位相减”的方法.

课本推导过程: 若{an}为等比数列,那么等比数列前n项和:Sn=a1+a2+a3+···+an-1+an=?,

分析已知: 我们现在仅学习了等比数列的定义以及等比数列通项公式:an=a1qn-1

那么上式就可以转化为Sn=a1+a1q+a1q2+···+

a1qn-2+a1qn-1=?

(1)注意观察每一项的特征,有何联系?

(2)比较①、②式,你有什么发现?

变式: 若新的数列改为cn=anbn,an等差数列,bn等比数列,求Tn.

分析: 新数列a1,b1,a2b2,a3,b3,...,an-1,bn-1,an,bn,它的前n项和是Tn=a1b1+a2b2+a3b3+···+an-1bn-1+anbn,根据等比数列的通项公式,上式可以写成

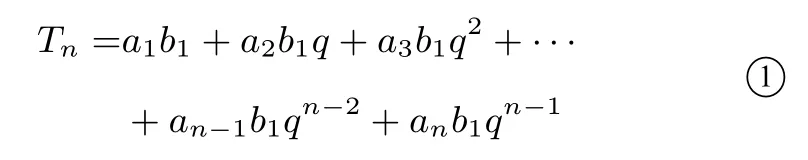
我们发现,如果用公比q乘以①的两边,就可以消去这些相同的项,得

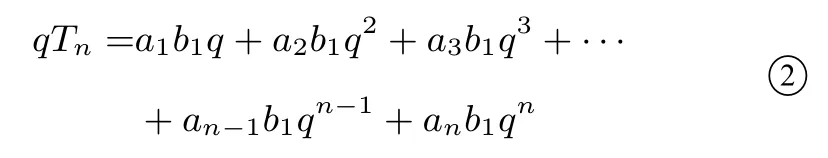
①②的右边有很多相同的项.用①的两边分别减去②的两边, 就可以消去这些相同的项, 得(1−q)Tn=a1b1+(a2−a1)b2+(a3−a2)b3+···+(an −an-1)bn −anb1qn,即(1−q)Tn=a1b1+db2+db3+···+dbn−anb1qn,即(1−q)Tn=a1b1+d(b2+b3+···+bn)−anb1qn,所以所以Tn=所 以如果学生理解等比数列前n项和的推导过程,那么对于教学片段2 的题目就会迎刃而解.

由此可见,在数学学习过程中,数学公式定理的产生推导过程对于数学的学习与理解起到十分重要的作用.在新高考模式下,越来越重视定理公式来源的理解与拓展.很多学生因为对于公式的理解不深刻,所在在做题时只是简单地模仿,这样带来的后果就是只要条件稍微改变就会出现“懂而不会”的现象,并且时间一长,就会很快遗忘.所以老师在教学中,要注重公式定理来源的引导,注重公式定理的推导过程,而非直接告知结论,因为推导过程中包含更多的是数学思想.

例2已知{an}是递增的等差数列,a2,a4是方程x2−5x+6=0 的根.

(1)求{an}的通项公式;(2)求数列的前n项和.

分析(1)方程x2−5x+6=0 的两根为2,3,由题意得a2=3,a3=2,在利用等差数列的通项公式即可得出;(2)利用“错位相减法”、等比数列的前n项和公式即可求出.考点:等差数列的性质;数列的求和.

2.2.2 在教学过程中,巧设问题

针对教学片段3 的第三问问题不是一下就能想到的,需要对问题进行分解.

为了解决第3 问,先设置两个小问题.

设置问题1.已知y=f(x)是定义在(−2,2)上的增函数,若f(m −1)

解因为y=f(x) 是定义在(−2,2) 上的增函数,f(m −1)< f(1−2m),所以联立解得.

设置问题2.kt2−2kt+2>0 对t ∈R 恒成立,求k的取值范围____.

解k=0 或⇒0

回到最开始的例题中,根据补充题目1、2,第3 问很快就可以求解出来.

(3)不等式f(kt2−kt)+f(2−kt)<0,由奇函数f(x)得到f(−x) =−f(x), 所以f(kt2−kt)< −f(2−kt) =f(kt −2),由f(x)在(−∞,+∞)上是减函数,∴kt2−2kt+2>0 对t ∈R 恒成立.∴k=0 或⇒0

综上: 0 ≤k <2.那么由上述两个小问题,再做教学片段3 的第三问,问题就迎刃而解.

由此可见,巧设问题,巧抛问题,会起到事半功倍的效果.这也符合新高考模式下对情景设计的要求.同时,对于高考题中综合性较强的题目,巧设、巧抛问题对于重难点的突破,强化数学思维都起到了很好的效果.所以教师在教学中,要注重问题的设置,问题的引导.

2.3 注重转化、创新能力.体现数学核心素养

在教学片段4 中,首先读懂题意,提取关键信息,找到有关变量,然后转化成数学问题,并对i进行分类讨论,从而求出j,k的值,题目就迎刃而解.

这道题体现了数学的分类讨论的数学思想,数学建模的核心素养，类似如例3 和例4.

例3(2020 全国1 文4)在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成1200 份订单的配货,由于订单量大幅增加,导致订单积压.为解决困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500 份订单未配货,预计第二天的新订单超过1600 份的概率为0.05.志愿者每人每天能完成50 份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至少需要志愿者( )

A.10 名 B.18 名 C.24 名 D.32 名

例4(2019 全国1 文4) 古希腊时期, 人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是( )

A.165cm B.175cm C.185cm D.190cm

例4 考查类比归纳与合情推理,渗透了逻辑推理和数学运算素养.采取类比法,利用转化思想解题.

3 总结

在新高考模式下,对老师提出了更高的要求,数学的考察不再是简单的计算与证明,更多的是数学思维与方法,同时越来越重视与实际生活相联系,以及数学核心素养的培养.但问题是,素养是无形的是无法教的.所以作为一线教师,不仅要仰望星空,更要脚踏实地.有效课堂教学该怎么做,核心素养如何落实在课堂,这是摆在我们教师面前的现实问题.