建立模型探究两角和的三角函数公式

广东省深圳实验学校初中部(518028) 邓 旭

近年的中考试卷中出现了个别“涉高题”,如用初中学段的知识比较繁琐,而用高中的知识极容易解决.从培养学生学习数学的兴趣和探究精神出发,老师不妨引导学生利用现有知识钻研探索,从而推导得出一些有趣、有用的结论,让学生更有成就感.两角和的三角函数公式的推导及应用本属高中教材中的内容,在初中阶段还不要求学生掌握,但在一些中考题中有所呈现,我们通过构建两角和模型,鼓励学生大胆探索推导出两角和三角函数公式,在理解公式的基础上应用解题,达到事半功倍的效果.

1 问题导入

例1 如图1,在边上相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB和CD相交于点P,则tan ∠APD的值为________.

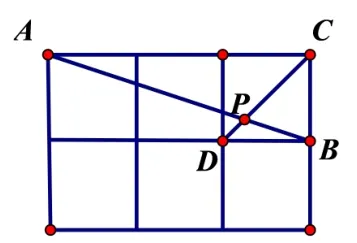
图1

常规解题思路: 如图2 , 连接BE交CD于F, 由题意易得BF=CF=DF, ΔACP∽ΔBDP, 由相似三角形的对应边成比例, 易得DP:CP= 1 : 3, 即可得PF:CF=PF:BF= 1 : 2, 在RtΔPBF中, 即可求得tan ∠BPF的值,继而求得答案.

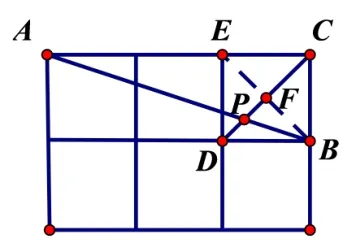
图2

由图1可知, ∠APD= ∠PAC+ ∠PCA, 且tan ∠PAC=tan ∠PCA= 1, 能否由此求出tan ∠APD的值,更值得期待的是,如果能找出两角和的三角函数公式,那么当点D移到其它格点(如D1,D2,D3,D4)位置时也能轻易求出tan ∠APD的值(如图3).

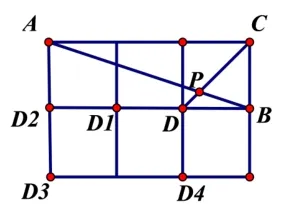
图3

2 模型探究

建立两角和的模型: 如图4,矩形ABCD中,E、F分别在边CD、AD上, ∠EBC=α, ∠EBF=β,EF⊥EB, 设BC= 1.能否用含α、β的三角函数表达式表示出其他的所有边.

图4

组织学生探索四个直角三角形:

(1)RtΔBCE中,CE=tanα,BE=.

(2)RtΔBEF中,BF=,EF=.

(3) RtΔDEF中, ∠DEF=α,DE= tanβ,DF=tanαtanβ.

(4)RtΔABF中,∠AFB=α+β,AF=AD −DF=1−tanαtanβ,AB=tanα+tanβ.

由此可得:

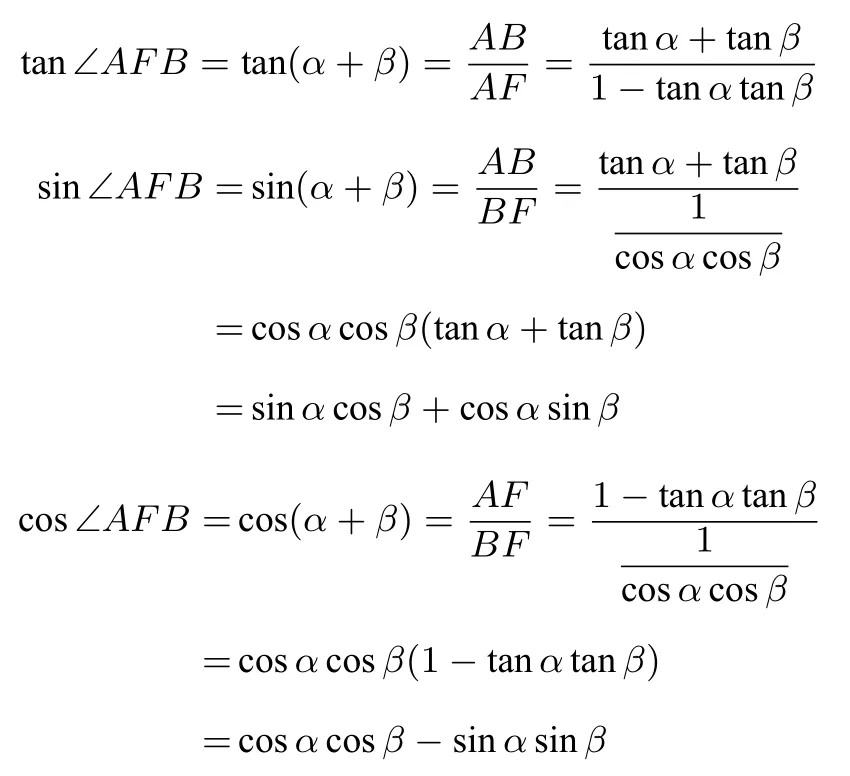
3 应用解题

应用2,如图5,抛物线y=ax2+bx+2 经过点A(−1,0),B(4,0),交y轴于点C;

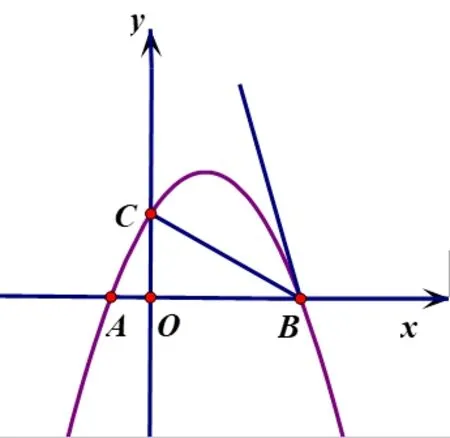
图5

(1)求抛物线的解析式(用一般式表示);

(2) 点D为y轴右侧抛物线上一点, 是否存在点D使若存在请直接给出点D坐标;若不存在请说明理由;

(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.

简析: 本题为深圳市2017年中考压轴题.

(1)、(2)皆常规题型,略.

(3) 求得直线BE解析式是关键, 联立直线BE和抛物线解析式可求得E点坐标, 则可求得BE的长.求得直线BE解析式方法多种, 如利用全等或相似等知识先求出直线BE上的一个点的坐标, 进而求得直线BE解析式; 还可以设直线BE与y轴交于点F, 由题可易求,tan ∠FBC= tan 45°= 1, 由公式tan(α+β) =得, tan ∠ABF= 3, 进而求得OF=12,直线BE解析式为y=−3x+12.