《圆锥的体积》教学设计

邹玉华

（湖南农业大学子弟小学 湖南·长沙 410128）

【教学内容】：人教版六年级数学下册第三单元《圆锥的体积》。

【教学目标】：

（1）理解圆锥的体积计算公式的推导方法，掌握圆锥的体积计算公式，并能运用圆锥的体积及其他相关计算，能解决简单的实际问题。

（2）通过“回顾旧知、方法与经验——大胆猜想——试验探索——合作交流——得出结论——实践运用”的探索过程，获得圆锥体积的计算方法和探究学习的方法，体会转化、推理、变中有不变等数学思想，提高解决问题的能力。

（3）培养学生勇于探索的求知精神，以及合作交流的良好习惯和团队协作精神。

【教学重难点】：圆锥体积公式的推导、理解，并能运用公式进行圆锥的体积及其他相关计算。

【学情分析】：

学生已经学会运用转化的思想推导出长方体、圆柱体积的计算公式，能利用公式进行计算，解决一些实际问题。对于小组合作探究的学习形式，学生已经熟知并喜欢，大部分学生会合作，会分工，会研究。对于本节课的内容——圆锥体积公式的推导，学生在已有的长方体、圆柱体积的推导经验的基础上，应该能自主探索，并发现规律，圆锥的体积是等底等高的圆柱体积的1/3。

【教法学法】：小组合作学习法。

【教具学具准备】：多媒体课件及等底等高圆柱、圆锥体积演示学具25套。

【教学过程设计】：

1 旧知回顾

（1）到目前为止，我们学过了哪些立体图形？

（2）你能利用公式计算哪些图形的体积呢?请说一说。

2 新旧知识迁移

出示课件：（橡皮泥、铁锥、小麦堆、木陀螺图）你能利用已学过的知识求出下列各圆锥的体积吗？

学生交流：

橡皮泥可塑性强，铁锥可沉入水底，小麦堆可用容器量。

木陀螺会漂浮在水面上，直接用排水法不合适，又不易变形，因此要求得它的体积很困难。

师导：刚刚同学们利用已学的知识来求圆锥的体积，这是一种什么样的数学思想？(转化思想)虽然同学们能利用转化的思想来求圆锥的体积，但都比较麻烦，能不能找到一种更简便的方法呢？

如果能找到圆锥体积的计算公式，那就方便了！

设计理念：此前学生已经历过长方体、圆柱的体积公式推导过程，能熟练利用转化思想来探求新图形与已学图形的联系。本环节的设计，意在巩固长方体、正方体、圆柱的体积计算公式，强化转化思想在解决数学问题中的重要作用，为探究圆锥的体积作铺垫。

3 引导学生了解学具，大胆猜想

（1）师导：根据以往经验，你们有什么想法吗？

圆锥与圆柱相近，它们之间会不会有联系呢？（出示课件：等底等高的圆柱和圆锥）。

（2）以小组为单位，拿出学具(圆柱和圆锥)，看一看，比一比，有什么发现？

师导：圆柱和圆锥的体积大小都跟底面半径和高有关。现在圆柱和圆锥等底（底面积）等高，它们的体积会不会有联系呢？

请同学们说说自己的想法。

设计理念：许多的发明与发现都源于猜想。这个环节能促使学生努力找寻新旧知识的联系，激发学生的探究热情，培养学生勇于探索的求知精神。

4 小组合作探究

等底等高的圆柱和圆锥的体积有什么关系呢？

（1）出示课件，展示合作探究内容与要求。

小组合作探究：等底等高的圆柱和圆锥的体积有什么关系呢？

合作要求：①两人一组，合理分工，一人操作，另一人观察并协助。②合作小组双方互换验证。③小组讨论，并填写好研究记录表。④探究过程中，尽量压低声音，以免影响其他同学和探究结果泄露。

（2）分小组试验，讨论，填好研究记录表。

方法一：先将 形容器装满水再倒入形容器中，_____次后，_______________。

方法二：先将 形容器装满水再倒入形容器中，_____次后，_______________。

通过试验，我们发现：____________________。

（3）全班交流（随机抽取三个小组交流实验过程、结果与发现）。

（4）引导小结：等底等高的圆柱的体积刚好是圆锥体积的3倍。

等底等高的圆锥的体积刚好是圆柱体积的1/3。

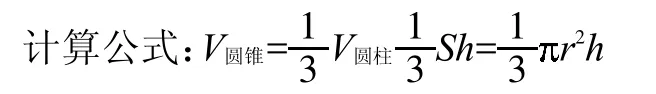
（5）引导学生分析：

①圆柱的体积是圆锥体积的3倍，等底等高的圆锥的体积刚好是圆柱体积的，在什么条件下？

②怎么选择合适的公式来计算圆锥的体积？

根据题目中给出的条件来确定计算公式：如果给出的是等底等高的圆柱的体积，则选用，如果题目中给出的是圆锥的底面积和高，则选用，，如果题中给出的是圆锥的底面半径或直径，则选用

设计理念：通过合作探究学习，一方面让学生通过自主探索求得圆锥体积的计算公式，能让学生更深刻地理解公式，从而更容易掌握公式，运用公式。另一方面通过合作学习，帮助学生进一步树立良好的团队意识，学会合作和交流，养成良好的合作习惯，同时，让学生的思维能力、动手操作能力、解决问题的能力等得到良好的锻炼与提升；在处事方式和人格修养等方面，通过互相借鉴，互相批评，互相鼓励，逐步形成良好的心理品质。同时，让基础薄弱的学生在团队中获得较大帮助，促进教学质量的全面提升。

5 学以致用

5.1 用公式计算下面各题

（1）有等底等高的一个圆柱和一个圆锥，圆柱的体积是36立方分米，圆锥的体积是多少立方分米？

（2）求下面圆锥的体积。

①底面的面积是120 cm2，高是15 cm。

②底面半径是3 cm，高是10 cm。

5.2 解决实际问题

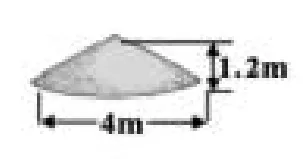
工地上有一堆沙子，近似于一个圆锥，底面直径是4米，高1.2米（如下图）。这堆沙子的体积大约是多少？如果每立方米沙子重1.5t，这堆沙子大约中多少吨？（得数保留两位小数。）

设计理念：第一题利用公式计算，旨在让学生进一步理解公式并能根据题目中给出的条件选择合适的公式进行计算，巩固新知。第二题的设计是将所学的知识应用于生活之中，进一步强化“数学源于生活，并服务于生活”的思想，提高解决问题的能力。

6 巩固拓展练习

（1）判断对错，对的画“√”，错的画“×”。

①圆锥的体积一定等于圆柱体积的1/3。（ ）

②等底等高的圆柱和圆锥的体积相等。（ ）

③如果圆柱和圆锥的体积和底面积相等，那么，圆锥的高一定是圆柱的高的3倍。（ ）

④把一块长方体的铁板锻造成一个铁锥，它们的体积一定相等。（ ）

（2）一个用钢铸造成的圆锥形铅锤，底面直径是4cm，高6cm。每立方厘米钢大约重7.8g。这个铅锤重多少克？（列算式不计算）

（3）一个圆锥形的零件，底面积是18cm2，高是12cm。把它锻造成一个长为6cm，宽为3cm长方体零件，这个零件的高是多少？

设计理念：设计巩固拓展练习，目的是帮助学生巩固新知，并将新知旧知融会贯通，举一反三，提高综合运用和解决问题的能力。