一道厦门市质量检测试题的探究

福建省宁德市高级中学(352000) 连其秀

题目(厦门市2021 届第一次质量检测第21 题) 已知椭圆C:= 1(a ＞b ＞0) 的左, 右焦点分别为F1,F2,|F1F2|=4,且a=

(1)求椭圆C的方程;

(2)若A,B为C上两个动点,过F2且垂直于x轴的直线平分∠AF2B,证明直线AB过定点.

本题的答案是: (1)椭圆C的方程为= 1; (2)直线AB过定点(4,0). 本题(2)的内涵丰富,具有探究价值,可引导学生进行适当的探究.

1 由特殊到一般的探究

本题(2)的结论表明: 直线AB过右准线与x轴的交点,即定点(4,0). 容易证明其逆命题也成立. 那么,对于一般的椭圆C:=1(a ＞b ＞0)这一结论成立吗?

经探究,这一结论以及其逆命题对于一般的椭圆仍然成立,即有

性质1设A,B为椭圆C:= 1(a ＞b ＞0)上的两个动点,直线l过椭圆C的右焦点F2(c,0)且垂直于x轴, 则直线AB过定点的充要条件是直线l平分∠AF2B.

证明设直线AB的方程为y=kx+n,与椭圆C的方程联立消去y并整理,得(a2k2+b2)x2+2a2knx+a2n2-a2b2=0. 设A(x1,y1),B(x2,y2),则x1+x2=-x1x2=由条件知直线F2A,F2B的斜率kF2A,kF2B均存在, 且kF2A+kF2B=又

则

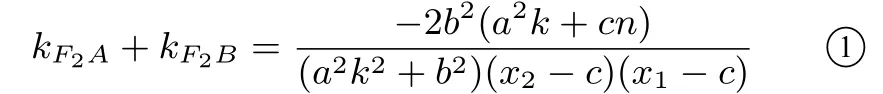
于是,直线l平分∠AF2B ⇔直线F2A,F2B的倾斜角互补⇔kF2A+kF2B=0⇔2b2(a2k+cn)=0⇔直线AB的方程为y=kx-直线AB过定点,0). 证毕.

注若在上述证明中以”t”替换“c”,容易将性质1 由右焦点F2(c,0)和定点(推广到类焦点F(t,0)(0＜|t|＜a)和定点的情形.本文从略.

2 由准线上的特殊点到准线上的任意点的探究

性质1 的直线AB过定点是右准线上的一个特殊点(右准线与轴的交点),如果直线AB过右准线上的任一定点P,那么会有什么相应的结论? 经探究,可得

性质Ⅰ设A,B为椭圆=1(a ＞b ＞0)上的两个动点,P是右准线上的定点,直线l过右焦点F2且垂直于直线PF2,则直线AB过定点P的充要条件是直线l平分∠AF2B.

证明设,r),r= 0 的情形即为性质1. 当r /= 0时,设直线l与直线AB的交点为Q,于是,

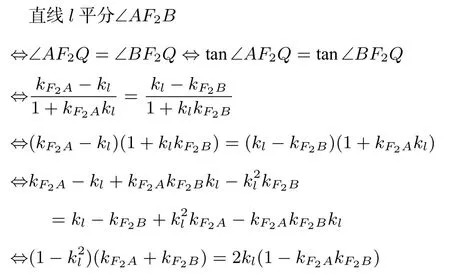
设直线AB的方程为y=kx+n,A(x1,y1),B(x2,y2),则

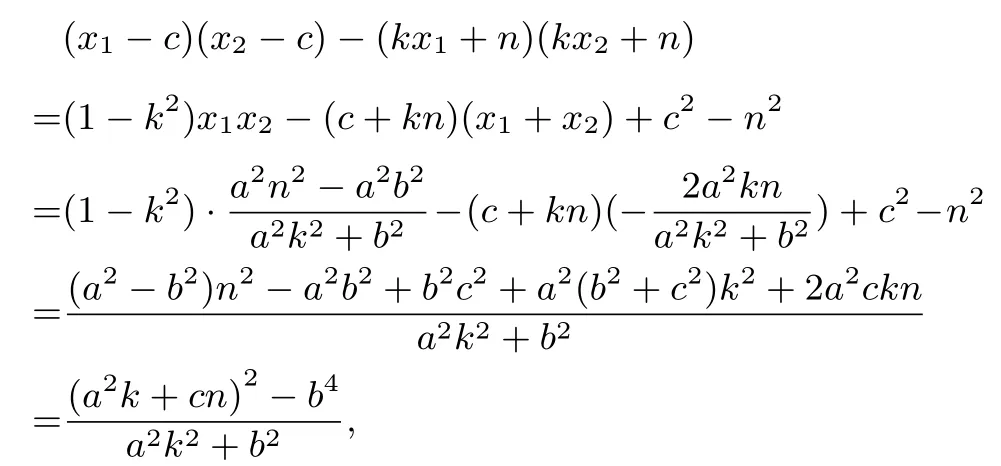
则

又直线F2P的斜率kF2P=则kl=1-k2l=1-由此及性质1 证明中的①式,可得

于是,

直线AB:y=kx+n过定点

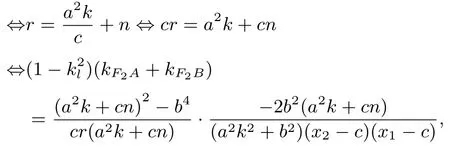
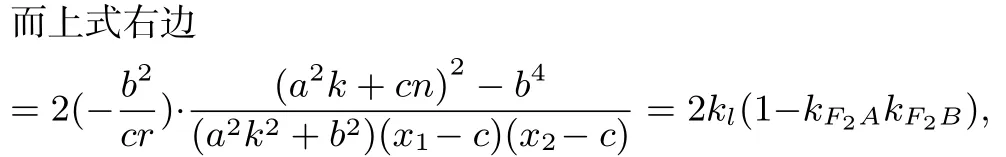
从而有直线AB:y=kx+n过定点(1-k2l)(kF2A+kF2B)=2kl(1-kF2AkF2B)⇔直线l平分∠AF2B. 证毕.

显然,上述性质1 可作为性质Ⅰ的推论.

3 由椭圆到双曲线、抛物线的探究

经探究,对于双曲线和抛物线,也有类似性质.

性质Ⅱ设A,B为双曲线C:=1(a ＞0,b ＞0)右支上的两个动点,P是右准线上的定点,直线l过右焦点F2且垂直于直线PF2,则直线AB过定点P的充要条件是直线l平分∠AF2B.

推论设A,B为双曲线C:=1(a ＞0,b ＞0)右支上的两个动点,直线l过双曲线C的右焦点F2(c,0)且垂直于x轴,则直线AB过定点的充要条件是直线l平分∠AF2B.

性质III设A,B为抛物线C:y2=2px(p ＞0)上的两个动点,P是准线上的定点,直线l过焦点F且垂直于直线PF,则直线AB过定点P的充要条件是直线l平分∠AFB.

推论设A,B为抛物线C:y2= 2px(p ＞0)上的两个动点,直线l过抛物线C的焦点且垂直于x轴,则直线AB过定点的充要条件是直线l平分∠AFB.

下面只证明性质III.

证明设直线AB的方程为y=kx+n(k /= 0), 与抛物线C的方程联立消去y并整理, 得k2x2-(2p -2kn)x+n2= 0. 设A(x1,y1),B(x2,y2), 据韦达定理, 得x1+x2=由条件知直线FA,FB的斜率kF A,kF B均存在,且

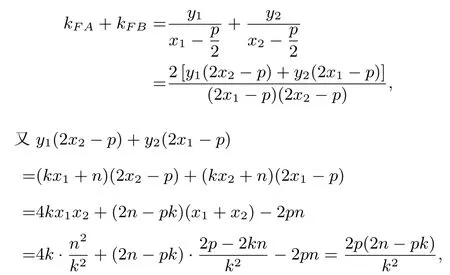
则

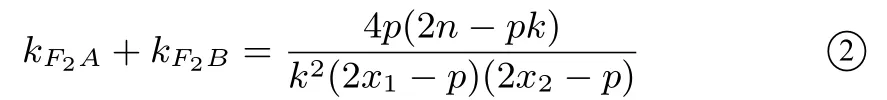
(1)当r=0 时,直线l平分∠AFB ⇔直线FA,FB的倾斜角互补⇔kF A+kF B= 0⇔4p(2n-pk) = 0⇔n=⇔直线AB的方程为y=kx+⇔直线AB过定点

(2) 当r /= 0 时, 类似性质1 的证明可得, 直线l平分∠AFB ⇔(1-k2l)(kF A+kF B)=2kl(1-kF AkF B). 由于

则

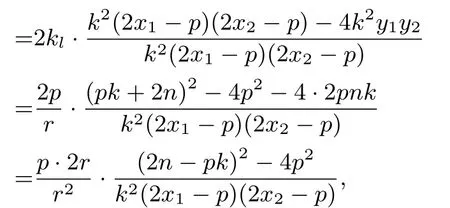
又直线FP的斜率则kl=由此及②式,可得

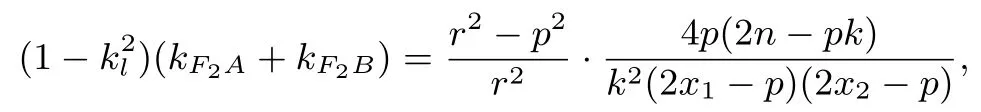
于是,

直线AB:y=kx+n过点

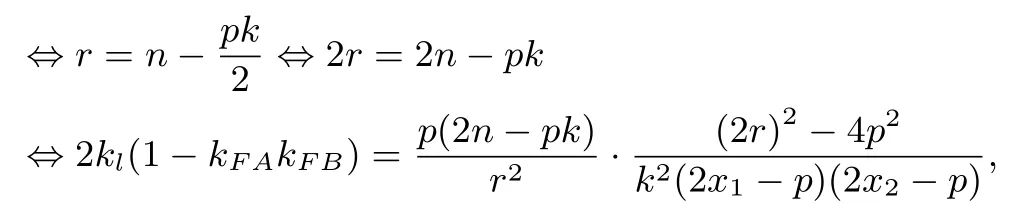
而上式右边== (1-k2l)(kF2A+kF2B), 从而有直线AB:y=kx+n过定点kF2AkF2B)⇔直线l平分∠AF2B. 综上,性质III 得证. 证毕.

至此,我们完成了对上述检测试题的探究.