一个新混沌系统分析及其电路实现
2021-11-18颜闽秀孙靖宇
颜闽秀, 徐 辉, 孙靖宇
(1.沈阳化工大学 信息工程学院, 辽宁 沈阳 110142; 2.工业环境-资源协同控制与优化技术辽宁省高校重点实验室, 辽宁 沈阳 110142; 3.北京首钢国际工程技术有限公司, 北京 100041)
Lorenz系统[1]是于1963年首次被提出的混沌系统,自其提出后,开创了混沌领域研究的篇章,促进了混沌理论的发展和应用.之后,不同类型的混沌系统不断地被发现,如Chen系统[2]、Lü系统[3]、Liu系统[4],而超混沌、分数阶、高维、多翼混沌也相继被提出[5-14].在1984年,Matsumoto[15]提出了双涡卷电路且首次搭建非线性电路将其实现,使其双涡卷电路模型成为研究混沌电路的经典模型.由于模拟电路能够有效地检测连续混沌系统的混沌特性,因此被广泛应用于混沌系统的验证.陈关荣[16]、吕金虎[17]、禹思敏[18]、包伯成[19]等对混沌系统的电路设计进行了深入研究,并在其专著中详细阐述了混沌电路原理.为了更深入探索混沌系统的工程应用,丰富混沌系统数量,寻找新的混沌系统十分必要.本文提出一个新型三维自治混沌系统,经理论分析和仿真验证其混沌特性,于Multisim软件中设计电子电路,模拟结果表明本文提出的混沌系统具有丰富的混沌特性.
1 系统模型及其相关特性分析
1.1 新混沌系统模型
提出的新混沌系统[系统(1)]数学模型为
(1)
式中:系统参数a,b,c,d,f,g是实常数,当a=-16、b=50、c=2、d=10、f=-8、g=4时,系统存在典型的吸引子,如图1~图4所示.由图1~图4可以看出:系统(1)的吸引子的几何形状非常复杂,具有很强的吸引性、复杂的折叠和拉伸轨线,轨线被限定在一个特定的区域内,是有界的.

图1 系统(1)的混沌吸引子
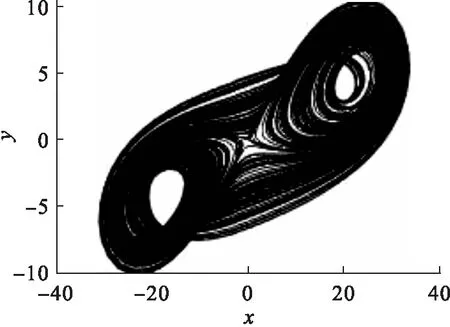
图2 x-y相图
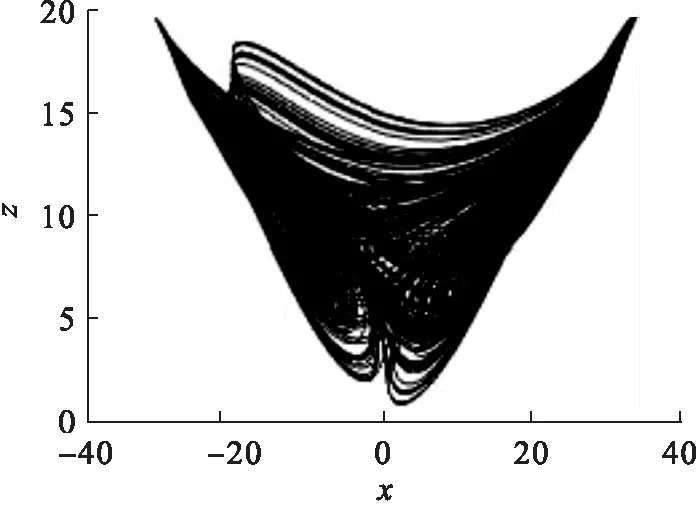
图3 x-z相图

图4 y-z相图
1.2 李雅普诺夫指数和维数
利用Matlab,通过正交法求得系统的李雅普诺夫指数为:λL1=2.392,λL2=0,λL3=-16.39.
计算李雅普诺夫维数DL为
(2)
由于系统(1)的李雅普诺夫指数分别为正、零和负,以及李雅普诺夫维数为分数,可以判断出系统(1)是混沌的[20].
1.3 系统的耗散性和吸引子的存在性
计算系统的能量函数∇V为

-16+10-8=-14<0.
(3)
所以系统是耗散的,且以
指数形式收敛,即体积元V0在时刻t时收缩至V0e(a+d+f)t=V0e-14t,即t→∞时,包含系统轨迹的每个体积元均以指数速率(a+d+f)收缩到零.所以系统轨迹都会被限制在体积为零的集合上,其渐近行为被固定在一个吸引子上,这说明了吸引子的存在性.
1.4 平衡点及其稳定性
令系统(1)式左边为0,即
(5)
解此方程,得到3个平衡点,分别为:A(0,0,0),B(24.2,4.904,12.03),C(-21.58,-4.959,12.3).
在平衡点A处对系统线性化,得到Jacobian 矩阵为
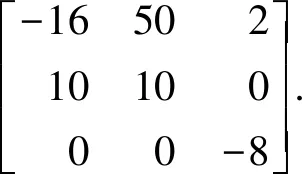
(6)
令det(J1-λI)=0,λ为特征值,I为单位矩阵.解得其特征值为:22.87、-28.87、-8,根据特征值的正负情况,分析出平衡点A为一个不稳定的鞍点.
同理,在平衡点B处线性化,得到Jacobian 矩阵为
(7)
解得其特征值为:0.899 4+31.86i、0.899 4-31.86i、-15.8, 因其特征值一个为负数,两个为正实部的共轭复数,所以平衡点B为一个不稳定的鞍焦点.
在平衡点C处线性化,得到Jacobian 矩阵为
(8)
解得其特征值为:0.733 4+30.63i、0.733 4-30.63i、-15.47,所以平衡点C为一个不稳定的鞍焦点.
综上所述,系统(1)具有1个不稳定的鞍点,2个不稳定的鞍焦点.
1.5 参数变化时系统的分岔图和李雅普诺夫指数谱
当固定参数b,c,d,f,g时,令a∈[-30,-10],绘制出系统关于x的分岔图以及李雅普诺夫指数谱,分别如图5和图6所示.
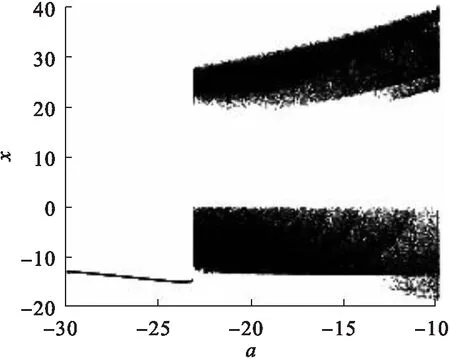
图5 a-x分岔图
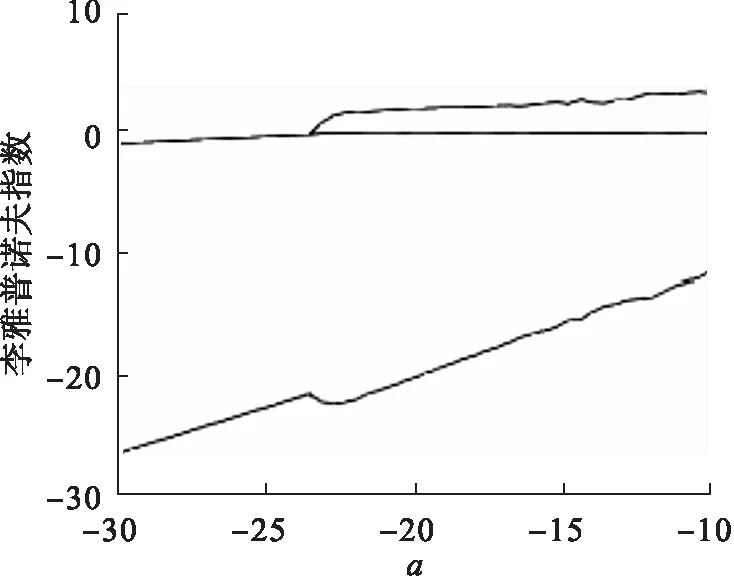
图6 李雅普诺夫指数
根据系统最大的李雅普诺夫指数是否大于0以及分岔图中有没有由点构成的成片的密集区域来判断系统是否处于混沌状态[18].从图5、图6可以看出:a在区间[-30,-23.4)上时,系统的李雅普诺夫指数均小于0,且分岔图没有出现由密集点构成的区域,此时系统处于周期状态;当a在区间[-23.4,-10]上时,系统最大李雅普诺夫指数大于0,系统处于混沌状态.
当固定参数a,c,d,f,g时,令b∈[-60,60],系统关于x的分岔图和李雅普诺夫指数谱分别如图7和图8所示.
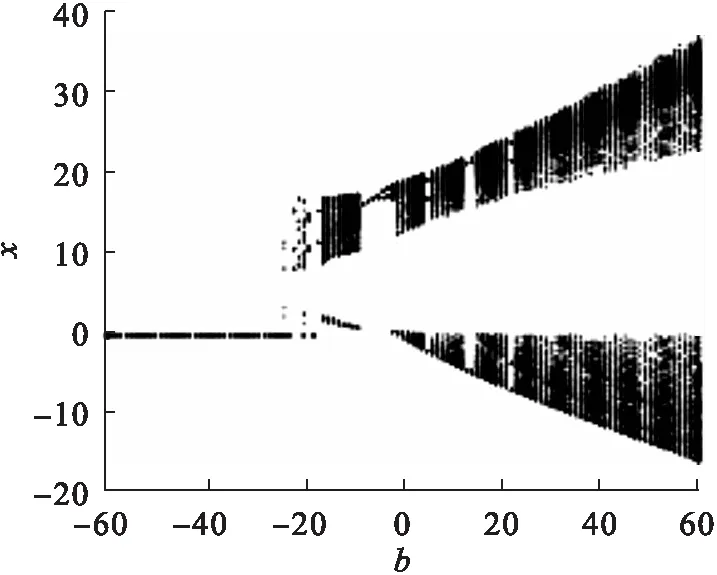
图7 b-x分岔图
从图7、图8可以看出:b在区间[-60,-19)上时,系统的李雅普诺夫指数均小于0,系统处于周期状态;b在区间[-19,-8]上时,系统最大李雅普诺夫指数大于0,系统由之前的周期状态进入混沌状态,分岔图在该区间内出现由密集点构成的区域;b在区间(-8,0]、[13,14]上时系统最大的李雅普诺夫指数小于0,系统处于周期状态;b在区间(0,5)、(5,13)、(14,22)、(22,60)上时,系统的李雅普诺夫指数大于0,系统处于混沌状态;在b=5、b=22处,系统最大的李雅普诺夫指数为0,系统处于周期状态,分岔图中出现分岔.
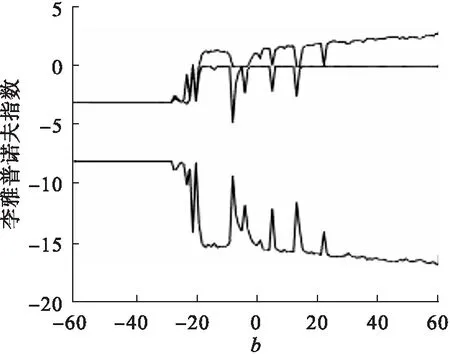
图8 李雅普诺夫指数
当参数c,d,f,g变化时,系统仍具有丰富的混沌特性,此处不一一赘述,只通过表格的形式给出参数变化对系统的影响(见表1).表1中的设置区间是当固定系统的其他参数时某一参数的变化区间,周期区间、混沌区间分别是出现周期和混沌现象的参数区间.
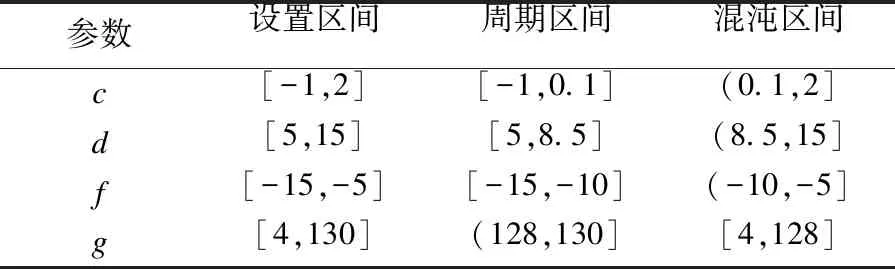
表1 参数变化对系统的影响
1.6 系统的频谱图及庞加莱截面图
系统的动力学特性还可以通过观察系统的频谱图和庞加莱截面图得到.当绘制庞加莱截面图时,庞加莱截面要选取恰当,不能包含系统的轨线,也不能与轨线相切.系统关于x的功率谱图和z=6、z=11、z=16关于xy平面的3个不同截面的庞加莱截面图分别如图9、图10所示.从图9可以看出系统的功率谱是连续谱,没有明显的波峰,并且峰值连成一片.从图10可以看出庞加莱截面图上有成片且具有分形结构的密集点,吸引子的叶片明显可见,再次说明系统(1)是混沌系统[18].

图9 功率谱图

图10 z关于平面xy的3个不同截面的庞加莱截面
2 电路设计与仿真
通过设计混沌电路进行模拟来判断文章提出的混沌系统能否物理实现,并对上述理论分析和仿真结果进行验证.通过Multisim设计实现该电路的原理图如图11所示.电路采用线性电阻、电容器、运算放大器、模拟乘法器(增益为1)设计实现. 其中:模拟乘法器用于实现系统中的非线性项;电容器用于实现积分运算;运算放大器及其相关电阻用于实现加、减运算.
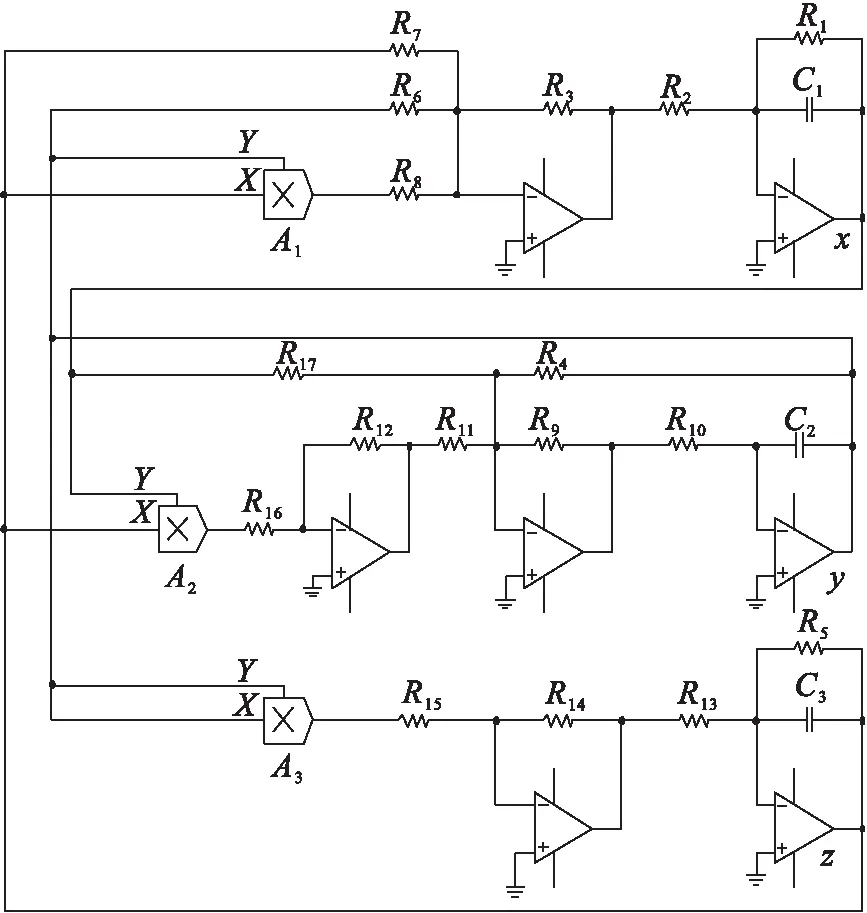
图11 混沌系统电路原理
根据电路原理和电路理论得到混沌电路的实现方程为
(9)
将式(9)与式(1)比较,可得
在(10)式作为约束条件下,令C1=C2=C3=1 μF,并取R1=62.5 kΩ,R2=R3=R6=20 kΩ,R7=R8=500 kΩ,R4=R9=R10=R11=100 kΩ,R5=125 kΩ,R13=R15=R16=R17=100 kΩ,R12=10 kΩ,R14=40 kΩ.基于以上数据对搭建的混沌电路进行仿真,仿真结果如图12~图14所示.从图12~图14可以看出电路模拟结果与上述理论分析以及数值仿真的结果一致,表明本文提出的混沌系统具有丰富的混沌特性.
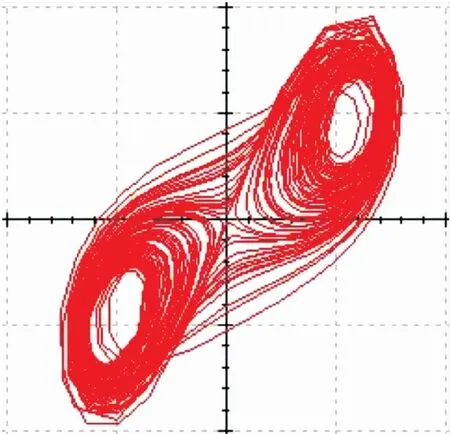
图12 U1-U2相图
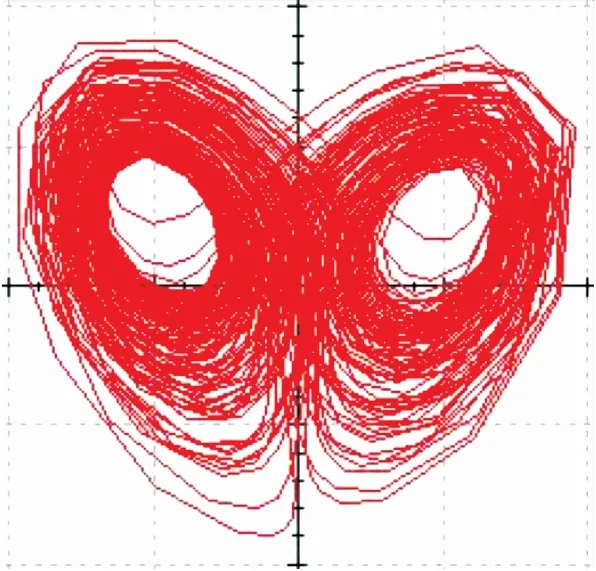
图13 U2-U3相图
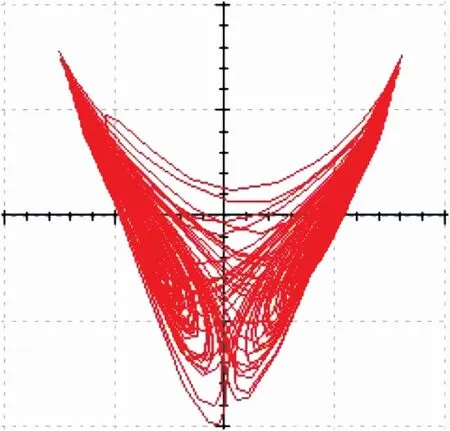
图14 U1-U3相图
3 结 论
本文提出了一个新的三维自治混沌系统,通过相关理论、Matlab仿真、李雅普诺夫指数和维数计算、耗散性、平衡点的稳定性、分岔图和李雅普诺夫指数谱、功率谱和庞加莱截面图分析新混沌系统的动力学特性.研究结果表明系统的吸引子是一个新的混沌吸引子,且由混沌系统模型搭建电路进一步验证证实了该系统的混沌特性.
