簧片式电磁振动台波形失真特性分析
2021-11-17胡天恩张旭飞
胡天恩, 张旭飞,2, 兰 媛,2
(1.太原理工大学 机械与运载工程学院,太原 030024;2.太原理工大学 新型传感器与智能控制教育部和山西省重点实验室,太原 030024)
随着加速度计等振动传感器在智能化生产、生活各领域应用越来越广泛,急需发展振动校准技术及装备,准确获取振动传感器的灵敏度等关键参数,为各类振动量值精确溯源及检测奠定基础[1]。振动传感器通常基于单频稳态原理进行校准[2],该原理规定由电磁振动台产生一定频率及幅值的振动信号,同时激励待校准传感器及已经过校准的标准检测系统(激光测振仪),比较两者输出可得到待校准传感器的灵敏度等参数。为保证更加稳定及接近单频的激励信号施加于待校准传感器,进而获取更高校准精度,国际标准推荐振动台输出的振动加速度波形失真度低于2%[3]。
为准确校准低频振动传感器,低频振动台通常需输出较大行程的振动激励信号,以获得足够的信噪比。但是,随着行程的增加,振动台结构参数的非线性不可避免会对输出振动信号产生影响,特别是板簧及乳胶管等回复弹簧刚度的非线性会造成输出振动信号产生严重的谐波失真。为此,Payne等[4]讨论了低频振动台谐波失真对稳态正弦激励低频振动校准的影响;魏燕定[5]基于振动台动力学方程,讨论了乳胶管弹簧非线性等因素导致的输出振动信号失真特性;陈晓建等[6]建立了振动台支撑结构强非线性动力学模型,分析了振动台的动力学特性;Li等[7]研发了一种用于低频光学加速度计校准的低成本、高精度簧片式振动发生器;何闻等[8]设计了十字簧片回复结构,有效改善了低频振动台的导向特性,降低了输出信号失真度;苏试公司[9]基于改进的弹性支撑装置,研发了一系列具有低失真动圈骨架结构的电磁振动台。此外,刘盈[10]分析了多种汽车悬架空气弹簧非线性刚度特性及相应的振动规律,为结构优化设计提供参考;Nicklich等[11-14]还分析了管线拖曳和横向振动等因素对乳胶管式振动台输出信号失真的影响。
综上所述,目前仅有学者针对低频振动台回复弹簧结构设计及输出波形失真理论计算等开展了研究。为进一步探讨簧片式低频电磁振动台的失真特性,本文基于有限阶幂级数非线性刚度假设,建立振动台状态空间表达式,通过理论计算、仿真分析及试验测试,深入研究刚度非线性等因素对输出波形失真的影响机理,为设计具有优化回复弹簧结构的低失真低频振动台及提高振动传感器校准精度提供理论及试验依据。
1 低频电磁振动台模型
传统电磁振动台可简化为图1所示结构,永磁体和内、外磁轭构成闭环磁路,驱动线圈嵌入与工作平台固连的动圈中。通入交流电流的驱动线圈在气隙磁场中受到安培力作用,推动动圈在回复弹簧作用下产生振动,进而为工作平台上安装的待校准传感器提供振动激励信号,完成校准过程。
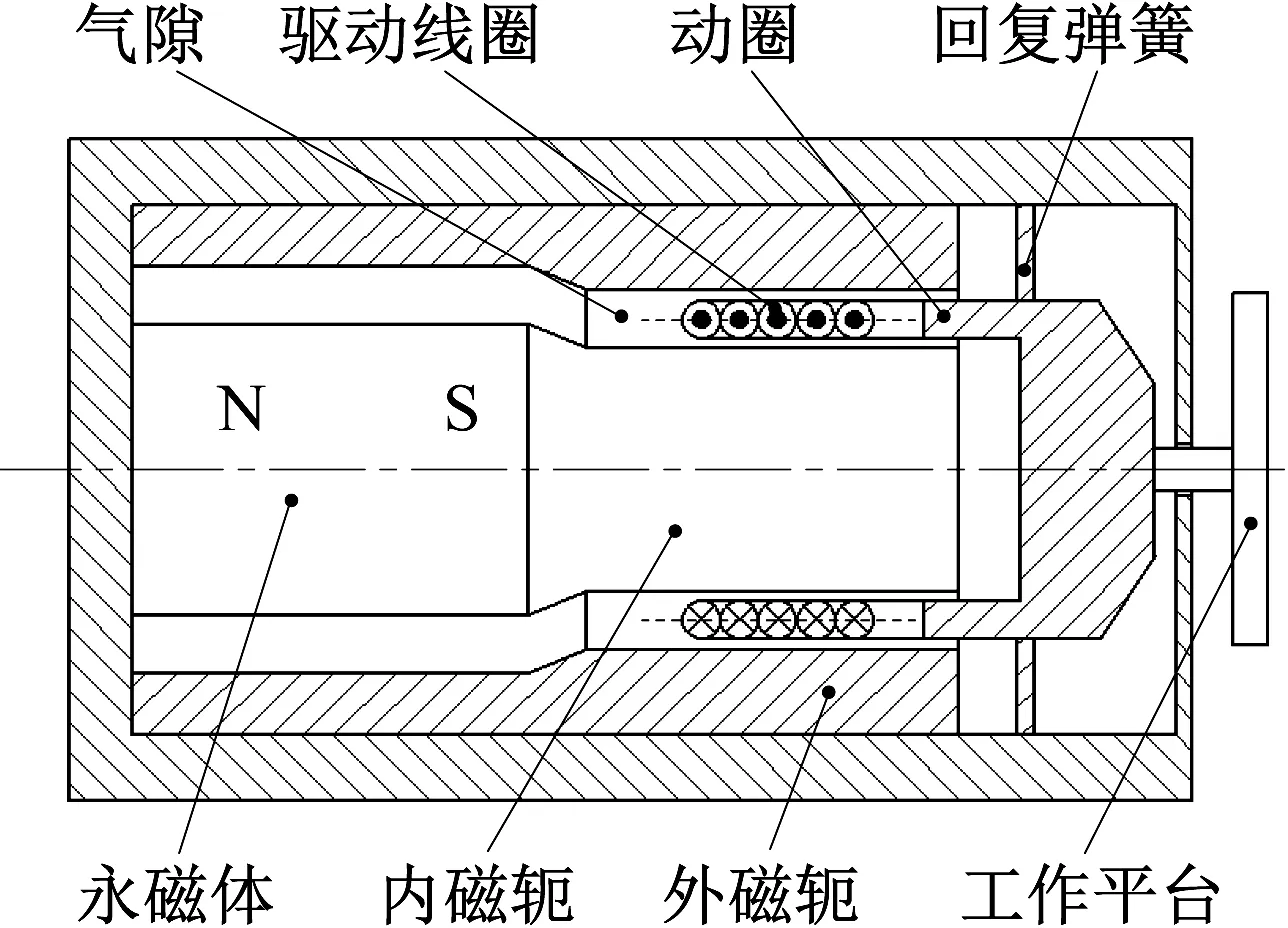
图1 电磁振动台简化结构Fig.1 Simplified structure of an electromagnetic vibrator
在低频段,工作平台、驱动线圈和动圈可视为刚性粘连的一体化运动部件,电磁振动台可简化为如图2所示的集总参数机电耦合模型,对应的运动方程为
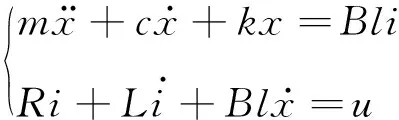
(1)
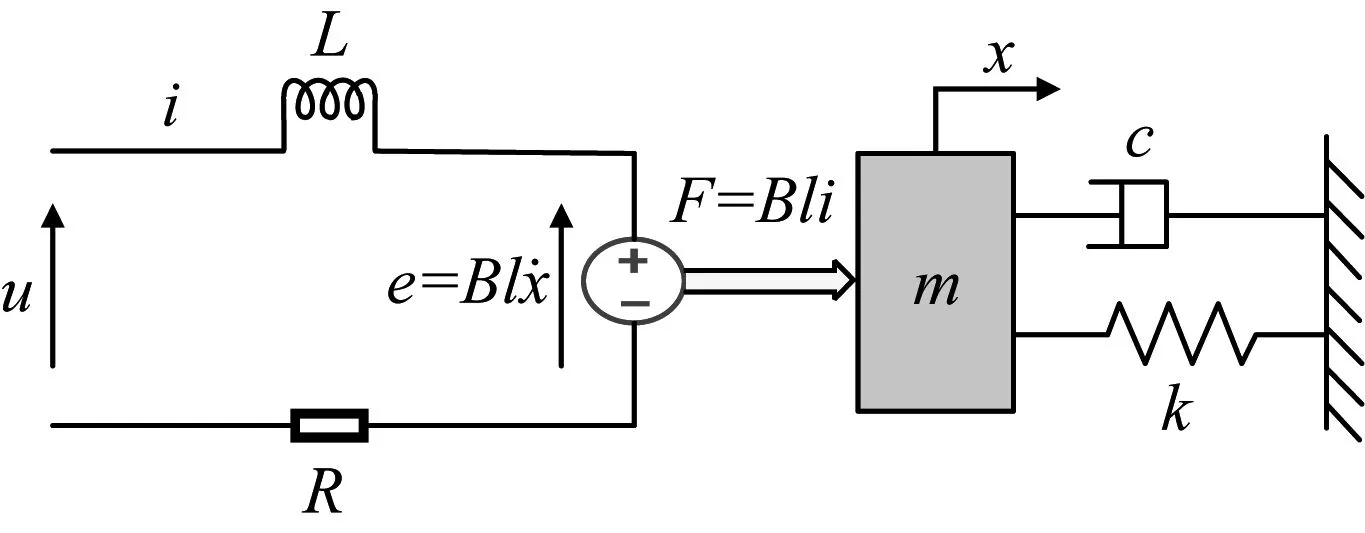
图2 机电耦合模型Fig.2 Electromechanical coupling model
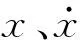
对于电磁振动台,参数m、l和R一般可视为常数,B也可通过优化磁路结构近似为常数,c和L为可忽略小量;但是,振动台回复弹簧刚度k在大行程振动时表现出明显非线性,即使标准单一频率正弦电流输入驱动线圈,输出信号也将不可避免产生较大谐波失真。
2 波形失真特性计算
考虑到簧片回复结构刚度随振动位移的变化而周期连续变化,可基于幂级数展开对非线性刚度k进行简化,进而计算大行程振动台输出信号的失真特性。
2.1 有限阶幂级数假设
一般情况下,即使针对低频振动台,簧片回复结构依然在小范围内形变,为简化分析过程,可将变形产生的非线性回复力Fk简化为前6阶泰勒级数
Fk=k0+k1x+k2x2+k3x3+k4x4+k5x5+k6x6
(2)
式中,k1~k6分别为各阶幂级数系数。考虑到回复力总与位移方向相反,而且平衡位置(x=0)的初始值为0,式(2)仅需保留奇次幂项,可简化为
Fk=k1x+k3x3+k5x5
(3)
将包含非线性系数k3及k5的式(3)替换式(1)中的线性项,可得频率ω的正弦输入电流对应的非线性运动方程为
(4)
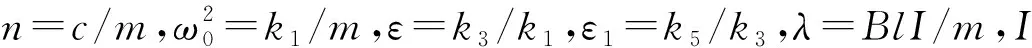
2.2 振动波形失真特性
假设式(4)的近似解为x=∑εsxs(s=0,1,2,…),其中,xs均为周期为2π/ω的函数,令ε的各次幂系数等于零,并代入式(4)可得
(5)
考虑到振动波形失真计算仅针对稳态情况,当阻尼系数n≠0时,可忽略瞬态解得到上式第一项的稳态解为
x0=X0sin(ωt-φ0)
(6)

(7)

x=x0+εx1=X0sin(ωt-φ0)+εX1sin(ωt-2φ0)+
εY1sin[3(ωt-φ0)-φ1]+εZ1sin[5(ωt-φ0)-φ2]
(8)
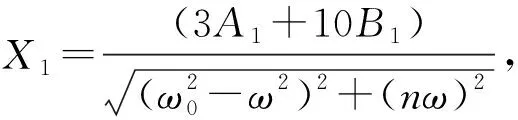
同理,可将求得的xs(s=1,2,…)逐次代入式(5)的第s项,可由第s次稳态近似解逐渐逼近非线性运动方 程的真实解。由假设的参数关系可知,随着非线性系数k3和k5的增加,式(8)中谐波成分的幅值将逐渐增大,导致更大的信号波形失真度,而对于具有确定簧片非线性特性的给定振动台,不同的输出信号基频及位移幅值等参数也将对应不同的波形失真特性。
3 仿真分析
基于上述计算结果,可首先辨识得到选定低频电磁振动台的非线性刚度系数,然后建立相应的仿真模型,分析不同频率及振幅输出振动信号的失真度。
3.1 非线性刚度辨识
图3所示为选定振动台的圆环状回复簧片模型,外环与振动台基体固支,内环连接运动部件,支撑臂连接内外环,起到支撑和柔性导向作用。

图3 圆环状回复簧片模型Fig.3 Model of the ring-type spring
为准确辨识图3结构的非线性刚度系数,用直流电源驱动振动台产生沿簧片平衡位置对称的若干静态位移,用以代表簧片产生的静态变形。由传感器检测得到该位移信号,并与输入激励电流产生的静态电磁力Bli比较,可近似计算得到簧片的非线性刚度特性。选取振动台的最大工作振幅±9 mm作为簧片最大变形量,可测试得到刚度-位移特性点分布如图4所示。基于式(3),可假设簧片的非线性刚度为4次偶阶多项式
k(x)=k1+k3x2+k5x4
(9)
由图4测试点可回归拟合得到该多项式为
k(x)=3 854.91+1 122.22×104x2+3 796.29×107x4
(10)
描述的刚度-位移特性曲线如图4所示,与实测值之间可求得决定系数R2≈0.996 1,与1非常接近,表明拟合多项式可以准确描述振动台的非线性刚度特性[15]。

图4 刚度-位移特性Fig.4 Stiffness-displacement characteristics
3.2 基于Simulink的仿真模型
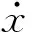
(11)
然后,基于式(11),可在Matlab/Simulink模块中建立如图5所示的近似非线性振动台仿真模型,相关参数如表1所示,其中,k1、k3、k5取式(10)求得的拟合值,其他参数由相应的试验测试得到。

图5 振动台仿真模型

表1 振动台参数
3.3 仿真结果分析
基于图5所示的仿真模型,可计算得到不同频率及振幅振动台输出信号的波形失真度值,对比分析选定簧片结构在不同频率及行程振动激励作用下的非线性特性及其对输出信号失真的影响。
首先,输入仿真模型0.1~10 Hz范围内若干选定频率的正弦电压信号u,使仿真模型输出不同频率下的等位移幅值(5 mm)振动信号x。在非线性回复弹簧作用下,输出的振动信号将产生谐波失真。考虑到振动加速度相对于速度及位移表现出更明显的失真特性,基于MATLAB中的FFT工具可计算出所有选定频率下的振动加速度失真度值,相应的频率-失真特性曲线如图6所示。此外,不同频率(1 Hz、2 Hz及3 Hz)对应的振动加速度波形对比如图7所示。由图6及图7可见,随着仿真频率的降低,振动加速度失真度逐渐变大,波形畸变更加严重,振动台表现出更大的非线性特性。其中,最低频率0.1 Hz对应的最大失真度达到16%,远大于国际标准推荐的2%。
然后,在上述选定的各频率点,输入仿真模型不同幅值的正弦电压信号u,使仿真模型分别输出位移幅值为2 mm及8 mm的振动信号,并计算得到相应的振动加速度失真度值,频率-失真特性曲线如图6所示。此外,频率为0.5 Hz对应的不同位移幅值振动加速度波形对比如图8所示。由图6及图8可见,随着仿真位移幅值的增加,所有频率下的振动加速度失真度均逐渐变大,波形畸变更加严重,振动台表现出更大的非线性特性。其中,0.1 Hz时最大位移幅值8 mm对应的最大失真度超过40%,远远大于国际标准推荐的2%。

图6 频率-失真特性曲线Fig.6 Frequency-distortion characteristic curves

图7 不同频率振动加速度波形Fig.7 Vibration acceleration waveforms with different frequencies
总体而言,由仿真分析结果可知,对于选定簧片结构,刚度非线性对振动台输出信号失真的影响规律为:振动行程(簧片形变量)的增加及频率的降低均使刚度非线性特性及对应的振动波形失真度增大。
4 试验测试
为验证上述理论计算及仿真分析的正确性,进一步建立试验平台,针对不同频率及幅值的振动信号失真特性开展试验测试。

图8 不同位移幅值振动加速度波形Fig.8 Vibration acceleration waveforms with differentdisplacement amplitudes
(1) 波形失真测试平台
如图9所示为建立的低频振动台输出振动波形失真测试平台,各装置型号及技术参数如表2所示。其中,信号发生器用于产生选定频率下具有极低失真度的标准输入电压信号,该信号经过功率放大器放大后,输入电磁振动台线圈中,驱动振动台产生目标振动信号。该振动信号由振动台运动部件上安装的加速度传感器及其电荷放大器检测。数据采集卡用于采集电荷放大器输出的模拟电压信号,并将该信号输入计算机,相应的计算机软件可以计算得到振动台输出振动加速度信号的幅值及失真度值。信号发生器、功率放大器及数据采集卡对试验测试的失真度影响通常可忽略不计。为提高测试结果的准确性,试验过程选用了失真度小于0.5%的加速度传感器,也可以基本忽略其对测试振动加速度信号失真度的影响。

图9 波形失真测试平台Fig.9 Test platform for waveform distortion

表2 试验装置型号及技术参数
(2) 测试结果分析
由图6可知,振动台加速度波形失真度在频率大于8 Hz后变化较小,而波形失真测试平台选用的加速度传感器的最低工作频率为2 Hz,所以试验过程选取2 Hz、5 Hz及8 Hz为测试频率,驱动振动台产生具有固定位移幅值5 mm的振动信号,实测得到的加速度波形失真度与相应的仿真值均列于表3。可见,试验与仿真失真度一致,误差在8%以内,由于振动台其他非线性因素及测试误差的影响,试验失真度均略大于仿真失真度。

表3 试验与仿真失真度值
此外,图10及图11所示结果表明,试验测试和仿真分析得到的2 Hz及5 Hz振动加速度波形具有相同的畸变规律。总体而言,试验测试结果验证了相关理论计算及仿真分析的正确性。
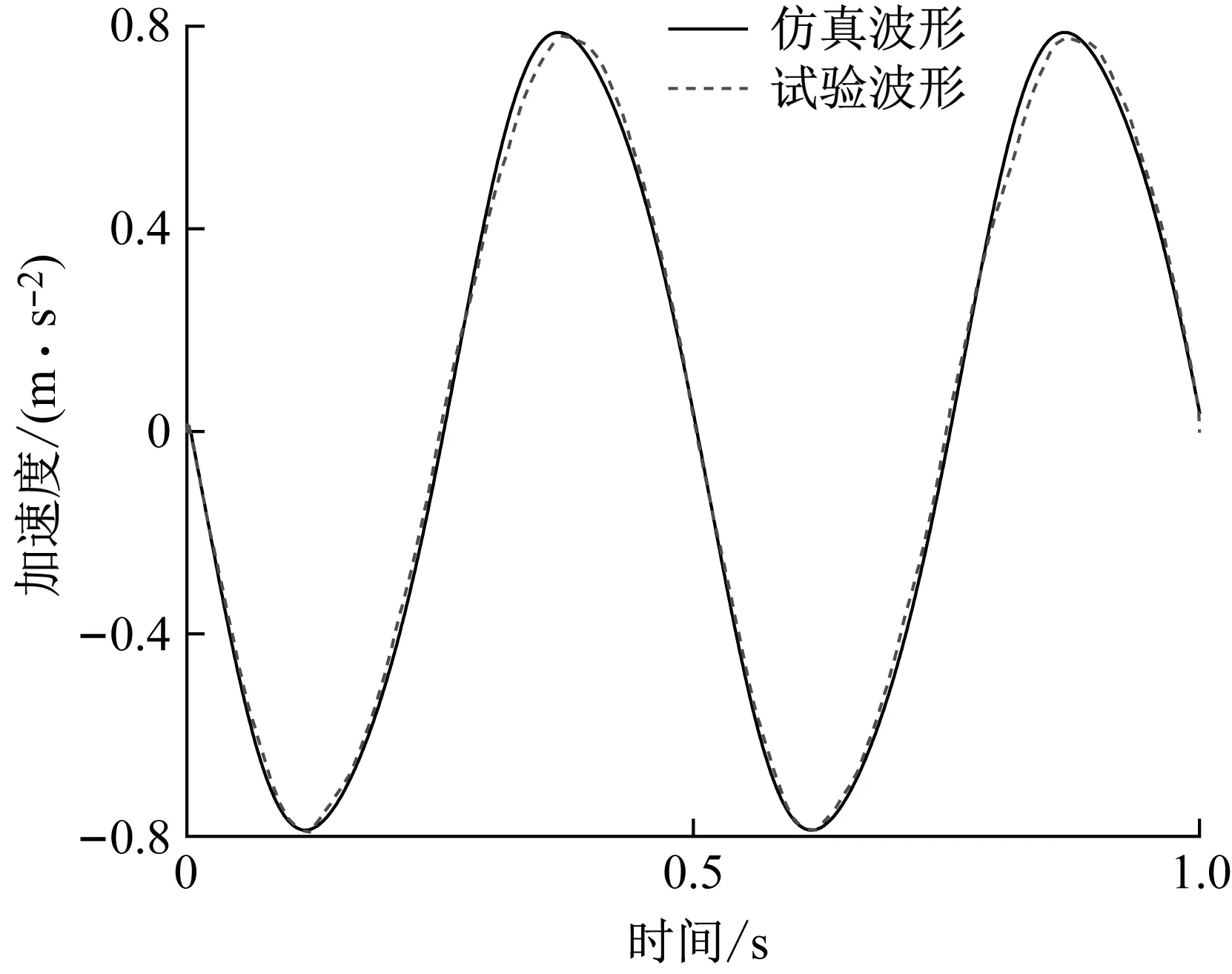
图10 2 Hz试验和仿真振动加速度波形Fig.10 Experimental and simulated vibration accelerationwaveforms at 2 Hz
5 结 论
针对簧片式低频电磁振动台大行程振动波形失真问题,本文基于有限阶幂级数非线性刚度假设,建立了考虑非线性因素的机电耦合模型及相应的状态空间表达式,进而通过理论计算及仿真,分析了具有特定非线性簧片的振动台波形失真机理,结果表明:振动台输出的基频振动位移幅值(簧片形变量)的增加及频率的降低均使刚度非线性特性及相应的波形失真逐渐增大。最后,通过试验测试不同频率及幅值输出信号失真度值及相应的振动波形,验证了理论计算及仿真分析的正确性。本文研究成果可为设计簧片式低波形失真电磁振动台提供理论及试验依据,并且可以进一步应用到其他形式的回复弹簧结构优化设计,为改善振动传感器校准系统的性能奠定基础。

图11 5 Hz试验和仿真振动加速度波形Fig.11 Experimental and simulated vibration accelerationwaveforms at 5 Hz
