船体加筋板耐撞性解析预报方法研究
2021-11-17赵延杰王海坤刘敬喜刘海蛟
张 敏, 赵延杰, 王海坤, 刘敬喜, 刘海蛟
(1. 武汉轻工大学 机械工程学院, 武汉 430048; 2. 中国船舶科学研究中心, 江苏 无锡 214082;3. 国防科技工业海洋防务技术创新中心, 江苏 无锡 214082; 4. 华中科技大学 船舶与海洋工程学院, 武汉 430074;5. 中国舰船研究设计中心, 武汉 430064 )
船舶在江海上运营时,由于天气、人为因素等原因,碰撞事故时有发生。若船舶碰撞事故发生,轻则使船体结构发生变形破坏,重则使船体进水甚至沉没,能造成巨大的损失。因此,合理评估船体结构的耐撞性以指导船体结构的耐撞性设计十分必要。
船体结构耐撞性评估方法主要有:模型试验法、数值模拟法和简化解析法[1-2]。模型试验法能获取结构物的碰撞损伤模式和载荷响应[3-4],但耗时较长。数值模拟法能模拟船体结构的损伤特征,计算船体结构抗碰撞载荷响应,但需准确校核单元的失效[5-6]。相对前两种方法,解析法的优势是能够快速评估船体结构的耐撞性[7-10]。在船撞舷侧场景中,撞击船船首一般是球鼻艏,在解析法的研究中,为简化计算过程,一般将球鼻艏简化为刚性球形撞头,且被撞结构物一般是船体局部结构——加筋板。然而,目前主要集中在光板的耐撞性解析研究。如:Wang等[11]考虑有限变形下圆板在球头撞击下的膜拉伸作用,提出了板的变形抗力和撞深计算公式;Simonsen等[12]基于板在球头压载下的整体稳定性,得到板的撞深和变形抗力公式,以及板的临界撞深公式;Lee等[13]考虑板初始破裂时刻的应力状态,结合数值模拟技术,提出了判断板初始破裂的计算公式;Gong等[14]将板的变形近似表达为对数函数和二次抛物线函数形式,运用里兹法求得板的变形抗力。
试验研究表明,相对于光板,加筋的添加使加筋板结构产生的变形抗力更大,但使其临界撞深变小[15]。因此,进一步开展加筋板耐撞性的解析研究是有必要的。加筋在板上一般是等间距分布的,但在抵抗外物撞击时,由于撞击位置的不同,加筋的类型有所区别。如图1所示,将撞头直接作用的加筋称为中间加筋;将未由撞头直接作用的加筋称为侧边加筋。两种加筋因变形驱动因素不同,变形模式存在区别。

图1 加筋的分类[16]Fig.1 Classification of the stiffeners
因此,本文开展了船体加筋板结构在球鼻艏撞击下的耐撞性解析预报方法研究。分别提出了板、侧边加筋和中间加筋的变形模式及其变形抗力计算公式;同时提出了预报加筋板临界撞深的计算方法。最终通过模型试验验证了所提解析解的准确性。本文提出的船体加筋板结构耐撞性解析预报方法对船体加筋板结构的耐撞性设计和评估有一定指导作用。
1 变形抗力计算
1.1 板的变形抗力
考虑尺寸为2a0×2b0(a0和b0分别为矩形板的半长和半宽)的矩形板受半径为r的球形撞头的侧向撞击作用。为简化处理,学者们一般将该类问题简化为轴对称问题。此外,对于撞击体质量较大,被撞物质量较小的低速碰撞问题,准静态压载下加筋板的变形模式和载荷响应与低速撞击下的结果接近[17]。因此,图2给出了圆形板在球头准静态压载下的变形模式。将板的变形模式置于ρ-w柱坐标系,ρ和w分别是板上任意一点到板边界的水平和垂直距离。此外,圆板的半径是矩形板的半宽b0,wp是板的撞深,C点是板与撞头接触的交界点,φc是C点与球头圆心所连直线与撞头对称轴之间的夹角。

图2 板的变形模式Fig.2 Deformation mode of the plate
板在大变形过程中主要受到膜拉伸作用,而弯曲作用较小。此外,板在发生面外变形时,不会发生面内变形,即:沿ρ方向的位移为0。因此,板的环向应变也可忽略(εθ=0)。仅考虑板的径向拉伸作用,其拉伸应变ερ可表示为
ερ=1/cosφ-1
(1)
式中,φ是板上任意一点与水平面的夹角。
考虑C点所在水平面以下板的变形区域,该区域同时受到球头向下的压载和板边缘的拉伸作用,在Ow方向,该区域的板受力平衡。因此,板整体承受的面外接触力F(φc)可以求得
F(φc)=σρ2πrsinφc·sinφctwp
(2)
式中:σρ是板的应力;twp是板变形后的厚度。
σρ用幂指数关系式表示为
(3)
式中,k和n分别是材料的强化系数和应变硬化系数。
将式(1)和式(3)代入式(2),得到板的变形抗力公式
F(φc)=2πktpr(1/cosφc-1)ncosφcsin2φc
(4)
式中,tp是板的初始厚度。
板的变形形式可以在ρ-w坐标系中用抛物线表示,并且假定抛物线的对称轴与球头顶端齐平。因此,当撞深为wp时,板变形形式可表示为
ρ(w)=aw2-2awpw
(5)
式中,a是待定系数,由式(9)决定。
C点坐标可以表示为
wc=wp-r+rcosφc
(6)
ρc=b0-rsinφc
(7)
C点是板与撞头的切点。因此,式(5)满足如下关系
(8)
将式(6)和式(8)代入式(5),可以求得系数a,表示如下
(9)
此外,C点也是板与撞头的交点。因此,式(5)也满足如下关系
ρ(wc)=ρc
(10)
将式(7)、式(9)和式(10)代入式(5),板的撞深可以表示为φc的函数
wp(φc)=
(11)
联合式(4)和式(11),可以同时得到由角φc决定的撞深wp(φc)及与撞深对应的变形抗力F(φc),即:变形抗力与撞深的关系。
1.2 中间加筋的变形抗力
由图1可知,中间加筋的变形由撞头驱动,其变形模式与板一致。图3给出了中间加筋的变形模式,中间加筋在变形过程中承受整体弯曲和膜拉伸作用。为简化计算,将未与撞头接触的变形区域简化为直线型,因此,中间加筋的弯曲作用集中在塑性铰处,如图3中阴影部分所示。
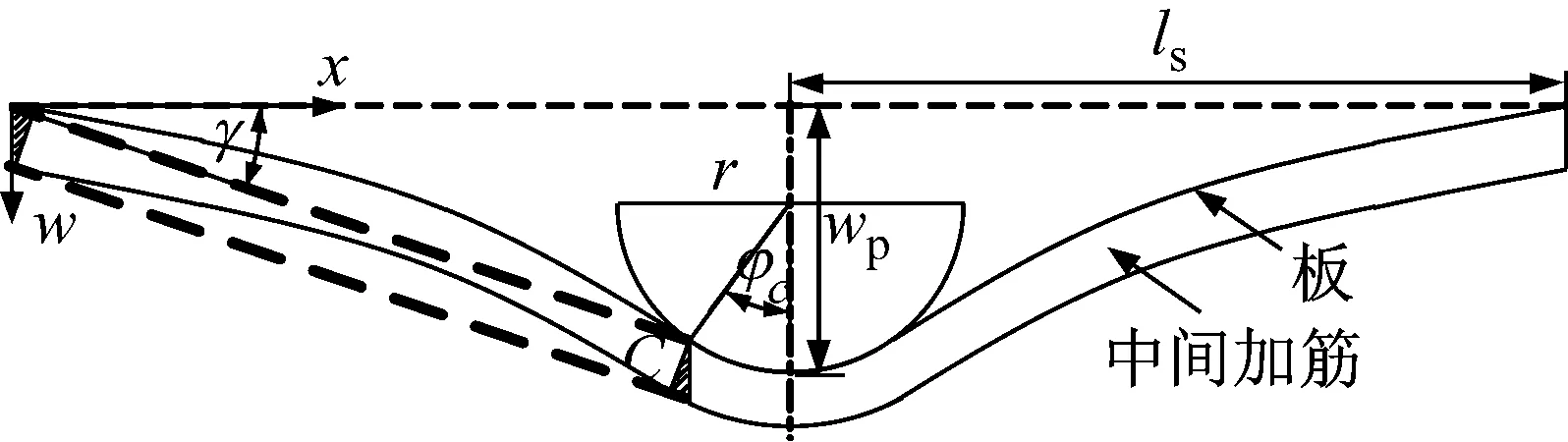
图3 中间加筋的变形模式Fig.3 Deformation mode of the central stiffener
中间加筋的转角γ可表示为
(12)
式中,xc是C点距加筋端部的水平距离。
此外,wc和wp有如下关系
wc=ccswp
(13)
式中,ccs是加筋在C点的变形量与加筋撞深的比值。
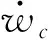
(14)
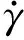
(15)
中间加筋的弯曲能量率可表示为
(16)
式中:ts是加筋的厚度;Mps是加筋单位尺寸的弯矩。由于中性面位于加筋板的板内[18],故Mps可表示为
(17)
式中:hs是加筋的高度;σ0s是加筋的流动应力,等于屈服应力和极限拉伸应力的平均值。
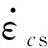
(18)
因此,加筋的膜拉伸能量率可表示为
(19)
式中,Scs是中间加筋单侧经历拉伸变形的面积,可表示为Scs=xchs。
根据上限定理,外力功率等于内力能量率,平衡方程可表示为
(20)
式中,Fcs是中间加筋的变形抗力。
将式(16)和式(19)代入式(20),Fcs可表示为
(21)
1.3 侧边加筋的变形抗力
加筋板变形过程中,侧边加筋与板之间存在耦合作用,板的变形驱动侧边加筋的变形;同时侧边加筋能约束板的变形。图4给出了侧边加筋在x-w直角坐标系中的变形模式,侧边加筋在变形过程中,整体承受拉伸作用;同时,侧边加筋两端会发生弯折。由于加筋面外弯曲单位尺寸弯矩比面内弯曲情形下小很多。因此,在计算侧边加筋变形抗力时,不考虑弯曲作用。侧边加筋的变形形式可表示为
(22)
式中:wls是侧边加筋的变形量;wlsmax是侧边加筋的最大变形量。
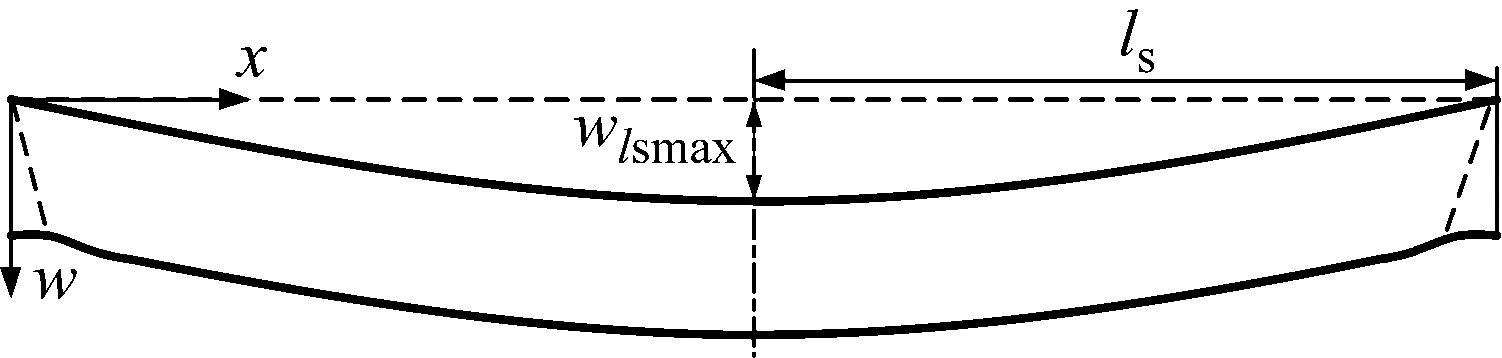
图4 侧边加筋的变形模式Fig.4 Deformation mode of the lateral stiffener
根据式(5),wlsmax可表达为
(23)
式中,xls是侧边加筋与板边的水平距离。
与中间加筋中的情形一致,对于侧边加筋,wlsmax和wp有如下关系
(24)
式中,cls是侧边加筋最大变形量与加筋板撞深的比值。
侧边加筋的拉伸应变可表示为
(25)
拉伸应变率可进一步表示为
(26)
侧边加筋的拉伸能量率可表示为
(27)
式中,Sls是侧边加筋的初始面积。
同样,根据上限定理,有如下平衡方程
(28)
因此,侧边加筋的变形抗力可以计算得到,表示为
(29)
2 临界撞深计算
2.1 光板的临界撞深
在船体壳板耐撞性评估中,壳板的初始破裂预报至关重要。目前,求取板临界撞深的方法主要有两种。第一种是计算板撞深与临界失效应变的关系,并用试验或数值模拟验证该临界失效应变值;第二种是基于板的整体稳定性,求得板的临界撞深。第二种方法中,板的破裂时刻与板变形抗力对撞深的一阶偏导为0的时刻一致,即∂F/∂wp=0[19]。事实上,通过该方法得到的临界撞深与板的拉伸应变表达式有关。本文所提变形抗力公式与文献[19]所提公式区别在于拉伸应变的表达式不同,若采用同样方法推导,最终得到的临界撞深公式会有差别。因此,本文引入一个修正系数,以确保预报结果的准确性。
式(4)中撞击力是夹角φc的函数。根据文献[19]中的方法,板的临界撞深取决于临界夹角φcf,当式满足∂F/∂φc=0,可以求得
(30)
求解式(30),可进一步得到
(31)
将式(31)代入式(11),去除小量,wpf可近似表示为
(32)
式中,c1是修正系数。
通过不同学者开展的模型试验校核得到c1值。表1总结了近些年学者们开展的球形撞头压载或撞击矩形板的模型试验,其中,文献[19]中的试验是低速冲击试验,测试试件有低碳钢和铝板,由于铝板的应变率不敏感性,因此将铝板试件所测得的数据进行校核。此外,对比几组数据发现,文献中模型试验的试件尺寸和撞头半径分布较离散,可确保所提临界撞深公式应用更广。
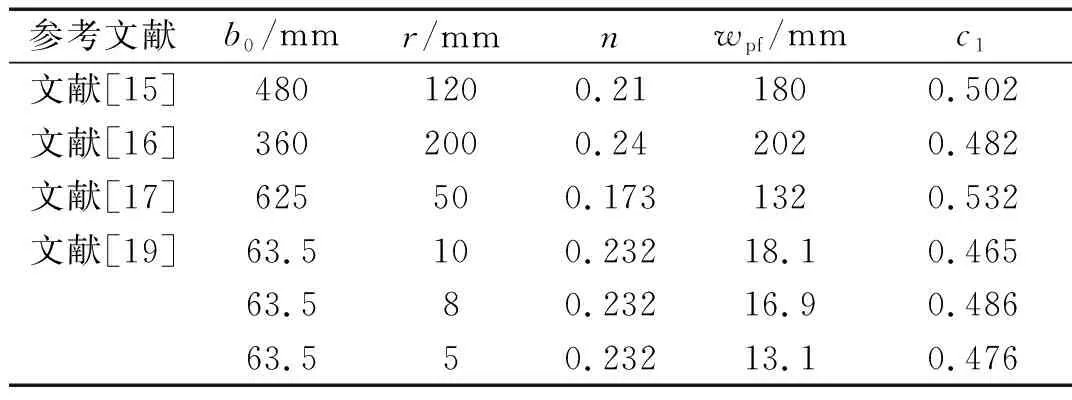
表1 文献中试验测得的临界撞深值
根据式(32),可计算得到每组试验的c1值,见表1。经计算,当c1值为0.49时,该组值的公差最小,将c1值代入式(32),光板的临界撞深可表示为
(33)
2.2 加筋的影响
侧边加筋能够约束板的变形,最终使板提前破裂。加筋板的临界撞深值wspf和板的临界撞深值wpf存在如下关系
wspf=wpf-dwls
(34)
式中,dwls是侧边加筋对板临界撞深的影响值。
对板筋交接处进行受力分析。板和加筋的耦合作用能使板的转角φ在板筋交接处不连续,如图5(a)所示,板既承受拉伸作用,即Fp1和Fp2;又承受侧边加筋的作用,即Fs。图5(b)是以侧边加筋的微元体作为研究对象,加筋承受板的反作用力,以及两端的拉力FNs,FNs可表示为
FNs=σ0stshs
(35)

(a) 板的受力
故图5(a)中由加筋提供的力Fs可表示为
(36)
式中,Rs是侧边加筋的曲率半径。根据式(22),可求得
(37)
此外,板自身的拉力可表示为
Fp1=Fp2=σ0ptpds
(38)
式中,σ0p是板的流动应力。
图5(a)中y方向合力为0。故Fs可表示为
Fs=Fp1(sinφ-sin(φ-dφ))
(39)
联合式(36),并将式(37)和式(38)代入式(39),板筋交接处板的转角变化量可表示为
(40)
根据式(5),板筋交接处的φ值满足如下关系式
(41)
根据式(41),侧边加筋对板临界撞深的影响值dwls可近似表达为
(42)
将式(40)代入式(42),dwls可进一步表示为
(43)
3 模型试验
本节开展模型试验以验证所提解析解的准确性。模型试验工装如图6(a)所示,自上至下依次为液压千斤顶、传感器、撞头和试件。其中,撞头顶部半径为75 mm,试件由上下夹具夹紧并由两排M20高强螺栓固定,加筋板试件中加筋两端与底座焊接固定,如图6(b)所示。加筋高度为55 mm,模型试件变形区域尺寸为600 mm×600 mm。试验过程中同步采集试件的变形抗力和撞头行进的位移,试验完成后,拍照得到试件的最终破坏形式。

(a) 试验工装
共开展了3组试件的模型试验,分别是光板试件US,2根加筋的加筋板试件2FB和3根加筋的加筋板试件3FB。试件详细尺寸和加筋布局如图7所示,每组试验需将试件压载至破裂。模型试件的板材厚度是3.15 mm,通过单轴拉伸试验可得到板材的工程应力-应变曲线,如图8所示。根据如下关系式
σtrue=σeng(1+εeng);εtrue=ln(1+εeng)
(44)
式中:σtrue和σeng分别是真实应力和工程应力;εtrue和εeng分别是真实应变和工程应变。
可以得到材料颈缩前的真实应力-应变曲线。材料的真实应力-应变关系可由下式表达
(45)
式中:σY是材料的屈服应力;εplat是材料屈服阶段结束时的应变值。
经曲线拟合,可得到k、n值,分别是690.2 MPa和0.2。材料属性值汇总于表2中。
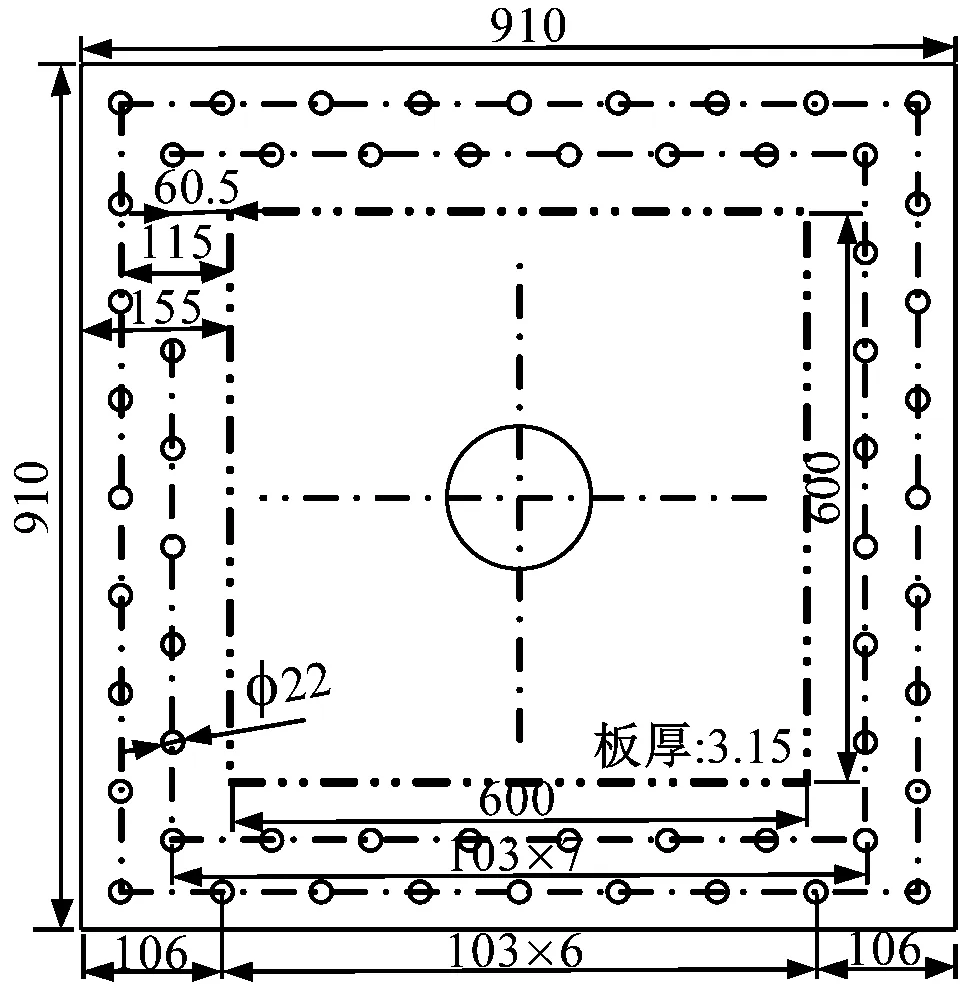
(a) 试件US
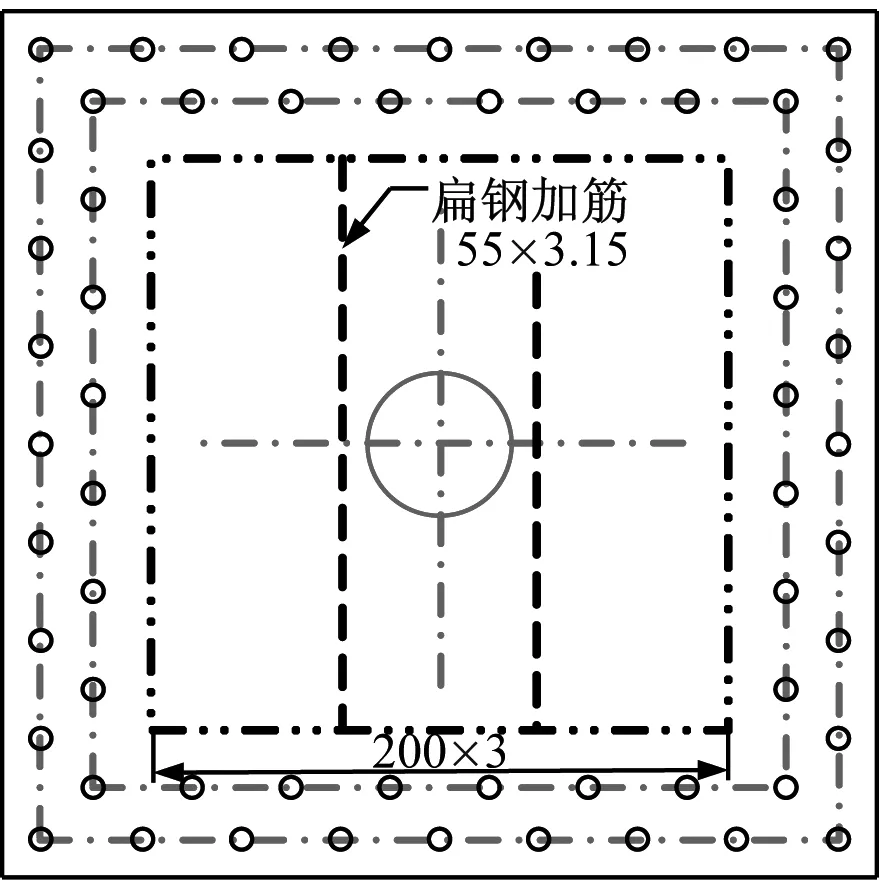
(b) 试件2FB (c) 试件3FB图7 模型试件尺寸(mm)Fig.7 Dimensions of the specimens (mm)

图8 板材材料曲线Fig.8 Material properties of the plate

表2 材料属性Tab.2 Material properties
4 解析解的验证
通过模型试验,得到了每组试件的最终破坏形式,如图9所示。同时,也得到了每组试件的变形抗力-撞深曲线。每组试件的变形抗力可由板、中间加筋和侧边加筋的解析公式叠加计算得到。对于加筋板的临界撞深,可由图10所示流程获取。通过式可计算得到板的临界撞深,通过式可计算dwls与φc之间的关系式,当式计算的wp(φc)与dwls(φc)之和与wpf接近时,即可得到侧边加筋对光板临界撞深的影响值,以及加筋板的临界撞深值。
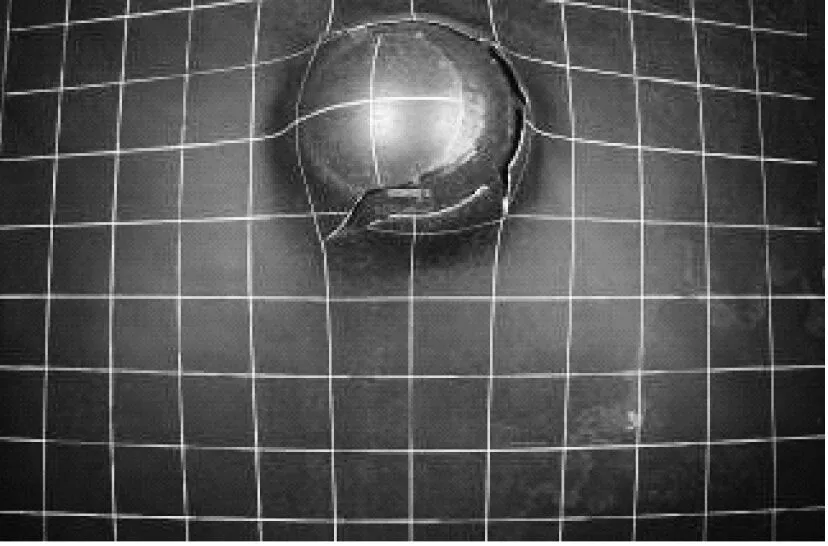
(a) 试件US

(b) 试件2FB
解析解与模型试验的变形抗力-撞深曲线对比如图11所示,3组曲线吻合良好,说明所提解析公式能准确预报球鼻艏撞击下加筋板发生大变形至初始破裂过程的载荷响应。

图10 加筋板临界撞深计算流程Fig.10 Workflow for calculating the critical penetrationdepth of the stiffened plate

(a) 试件US
5 结 论
本文提出了船体加筋板结构在球鼻艏撞击下发生变形至破裂过程的解析预报方法。所提解析方法包括:
(1) 加筋板的变形抗力计算。假设光板的抛物线变形模式,分别提出了光板的变形抗力和撞深计算公式;将加筋分为中间加筋和侧边加筋,分别提出两类加筋的变形模式,并结合塑性力学上限定理,推导了两类加筋的变形抗力-撞深计算公式。
(2) 加筋板的临界撞深计算。基于板变形过程的稳定性,初步获取板的临界撞深公式,并通过已有试验校核相关参数,最终得到了板的临界撞深计算公式;考虑板与侧边加筋的耦合作用,推导了侧边加筋对光板临界撞深的影响计算公式;两者结合,可计算加筋板的临界撞深。
开展了模型试验,验证了所提解析方法的准确性,本文所提解析预报方法对船体加筋板结构的耐撞性快速预报和评估有一定指导作用。
