两对称建筑干扰下的超高层建筑风荷载及风效应研究
2021-11-17余先锋林益新谢壮宁
余先锋, 林益新, 谢壮宁
(华南理工大学 亚热带建筑科学国家重点实验室, 广州 510640)
高层建筑风荷载和风致响应的干扰效应,一直是结构风工程关注的热点。已有文献主要集中在两个方形或矩形截面高层建筑的风致干扰效应上[1],且较少涉及基底扭转荷载[2-5]和顶部加速度[6-7]的干扰效应。由于问题的复杂性,三建筑间的风致干扰效应研究相对较少,但其影响不容忽视。Saunders等[8]研究了在上游不同位置的两栋施扰建筑对下游受扰建筑的影响,发现两侧对称施扰建筑下的基底荷载最大干扰因子较相应单侧布置施扰建筑下的结果高80%。在上游两建筑施扰下,Kareem[9]研究了受扰主建筑在4个特定施扰位置时的基底荷载干扰效应,试验结果与上游单栋建筑施扰产生的干扰效应相近,这可能是由于其施扰位置较少,导致其试验结论偏片面。Xie等[10-15]通过风洞试验系统研究了三栋高层建筑间的基底荷载干扰效应,结果表明三栋建筑之间的动力干扰效应较两栋建筑更为明显,在B类地貌且折算风速vr(vr=vH/(f0b),其中vH为结构屋顶高度H处的参考风速,f0为结构的固有频率,b为受扰建筑的特征宽度)为8时的干扰因子较两栋建筑的试验结果增大了80%,即使在D类地貌,二者仍有25%~30%的显著差异。
实际工程中多为两栋及以上周边建筑的情形,因此开展上游两对称建筑干扰下的超高层建筑风荷载和风效应研究,对完善三建筑间的干扰效应研究并对超高层建筑的抗风设计有重要理论意义和工程价值。
文中通过多工况建筑模型同步测压风洞试验,获取上游两对称高层建筑布置时的受扰主建筑表面时变风荷载,并由风振计算获得结构的基底荷载响应和顶部加速度响应。在此基础上,研究受扰建筑的基底气动力干扰因子(aerodynamic interference factor, AIF)、基底荷载响应和顶部加速度响应包络干扰因子(enveloped interference factor, EIF)的分布规律。
1 风洞试验概况
风洞试验是在一试验段截面尺寸为3 m×2 m的大气边界层风洞中进行的,试验照片如图1所示。按 GB50009—2012《建筑结构荷载规范》[16]模拟了C类地貌风场。模拟的平均风速剖面、湍流度分布以及屋顶高度处的功率谱密度如图2所示,图中VH为屋顶高度处的平均风速,Lu为屋顶高度处的湍流积分尺度。
试验主模型(受扰建筑)的横截面尺寸为100 mm×100 mm,高度为600 mm,按1∶400的几何缩尺比模拟240 m高的超高层建筑。试验模型上一共布置了7个测压层,各层测点布置情况如图3所示,共计196个测点。

图1 风洞试验照片Fig.1 Image of wind tunnel test

(a) 平均风速剖面和湍流度分布

(b) 屋顶高度风速谱图2 C类地貌风场参数模拟结果Fig.2 Simulated wind parameters in terrain category C
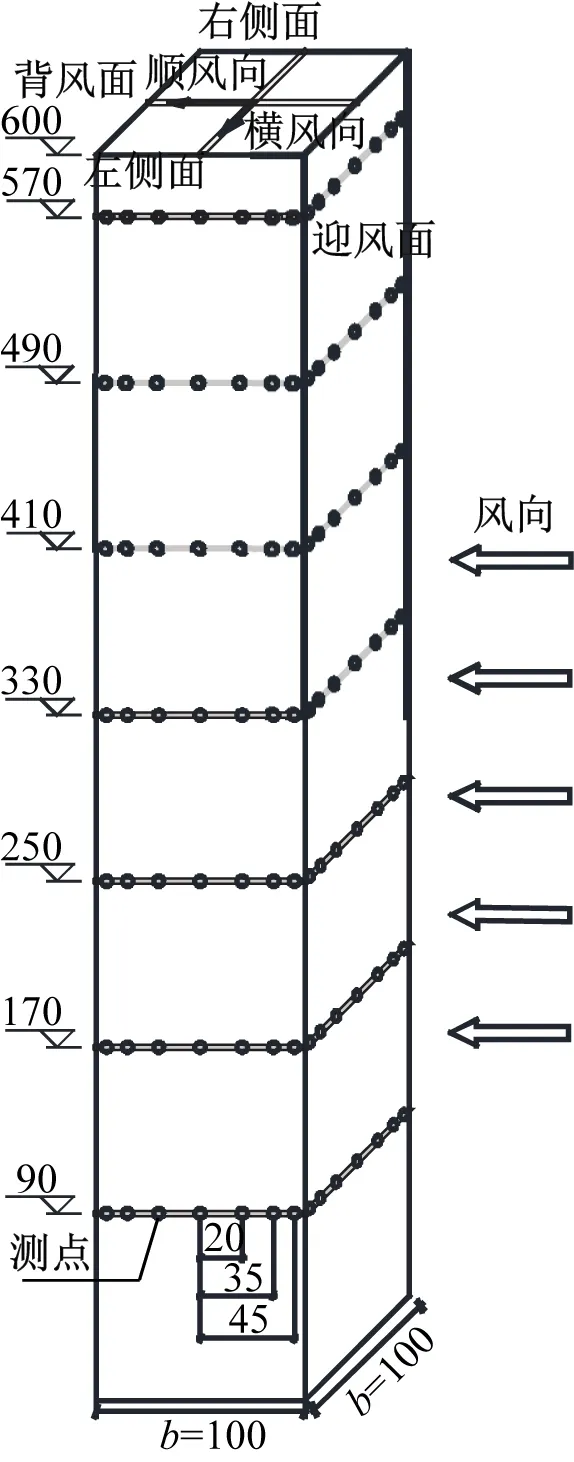
图3 各层测点布置(mm)Fig.3 Tap location on each tap floor (mm)
受扰建筑A与两对称施扰建筑B和C等截面等高,试验坐标系统如图4所示。图中风向角和受扰建筑A的位置保持不变,施扰建筑B和C以受扰建筑A的中线对称布置。b为受扰建筑和施扰建筑的截面宽度,x和y分别代表受扰建筑与施扰建筑的纵向间距与横向间距。试验采样时间65.536 s,采样频率为312.5 Hz,每个通道的采集数据为20 480个。

图4 风洞试验坐标系统Fig.4 Coordinate system of wind tunnel test
2 数据处理及风致响应计算
2.1 基底气动力

(1)
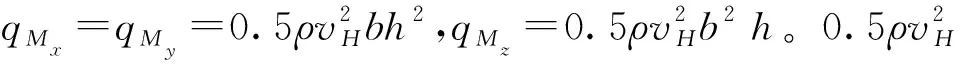
为了详细评估基底气动力的干扰效应,采用基底气动弯矩干扰因子(AIF)以评估顺风向、横风向和扭转向的气动力干扰效应,即:
(2)
2.2 荷载峰值响应
(1) 首先采用完全二次型组合(CQC)方法计算超高层建筑在脉动风荷载作用下的位移响应,其中广义位移标准差σy为
(3)
式中:|H(ω)|为系统的频率响应函数;Sf(ω)为广义力f(t)的功率谱密度;ω为频率。
(2) 基于GLRC原理计算各楼层等效静风荷载FESWL,其中对模态响应矩阵的计算是采用直接积分计算方式,不再做背景和共振部分分解的近似处理。
(3) 进一步由各楼层FESWL计算基底弯矩响应和扭矩响应。
(4)
在折算风速vr=2~11下进行受扰建筑基底弯矩响应计算,在折算风速vr=2~5下进行受扰建筑基底扭矩响应计算,在折算风速vr=2~6下进行受扰建筑顶部加速度响应计算。为考虑周边建筑的干扰影响,定义基底峰值荷载响应和结构顶部加速度响应干扰因子(interference factor of responses, RIF)为
(5)
为便于工程应用,进一步对不同折算风速vr下的干扰因子RIF进行包络,采用更具代表意义的干扰因子包络值EIF分析基底弯矩响应和结构顶部加速度的干扰效应,即:
EIF=max(RIF(vr))
(6)
3 试验结果分析
3.1 基底气动力干扰因子
图5给出了上游两侧对称建筑干扰下的顺风向基底气动弯矩干扰因子AIF随串列间距比x/b的变化。从图5(a)可以看出,顺风向平均AIF均小于1,表现为遮挡效应。上游两侧对称建筑横向距离较大(|y/b|=1.8)时的顺风向平均AIF远大于其横向距离较小(|y/b|=0.9)时的结果,并且它随着串列间距比x/b的减小而逐渐增大,即其遮挡效应随着串列间距的减小而逐渐减弱。对于横向距离较小(|y/b|=0.9)的情形,当x/b≥4时,顺风向平均AIF基本保持不变,但当x/b≤4时其随着串列间距的减小而急剧增大,即对称施扰建筑离受扰建筑越近,遮挡效应反而越弱,这可能是对称施扰建筑间的峡谷放大效应抵消了部分遮挡效应所致。
从图5(b)可知,上游两侧对称建筑横向距离较大(|y/b|=1.8)时顺风向基底气动弯矩均方根的AIF也大于其横向距离较小(|y/b|=0.9)时的结果。当横向间距较小(|y/b|=0.9)时,不同串列间距比x/b下的AIF皆表现为遮挡效应,而对于横向间距较大(|y/b|=1.8)情况,在串列间距比x/b为4和5时的AIF却大于1,表现为放大效应。
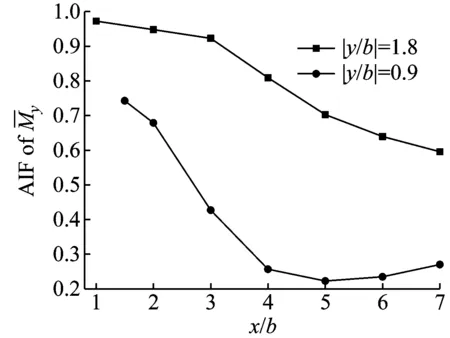
(a) 平均值

(b) 均方根值图5 顺风向基底气动弯矩干扰因子Fig.5 AIF for the along-wind base moment
上游两侧对称建筑干扰下的横风向基底气动弯矩均方根AIF随串列间距比x/b的变化,如图6所示。由图6可知,各串列间距下的横风向均方根AIF均小于1,表现为遮挡效应,尤其是上游两侧对称建筑横向间距较小时的横风向均方根AIF低于0.6,呈现强遮挡效应。当x/b≥2时,横向间距较大(|y/b|=1.8)时的横风向均方根AIF总是大于横向间距较小(|y/b|=0.9)时的结果,即上游两侧对称施扰建筑的横向间距越大,对横风向基底气动弯矩的遮挡效应越弱。
图7给出了不同串列间距比x/b下的气动扭矩均方根AIF的变化。从图中可知,各种x/b下的气动扭矩均方根AIF也都小于1,呈现遮挡效应。当串列间距比为2≤x/b≤3时,横向间距较大(|y/b|=1.8)时的气动扭矩均方根AIF小于横向间距较小(|y/b|=0.9)时的结果,而对于其它串列间距比x/b,横向间距较大(|y/b|=1.8)时的气动扭矩均方根AIF却大于|y/b|=0.9下的结果。

图7 扭转向基底气动力均方根值干扰因子Fig.7 AIF for the RMS torsion moment
3.2 基底荷载响应干扰因子
不同串列间距比x/b下,上游两侧对称建筑干扰时顺风向基底峰值弯矩响应干扰因子EIF的变化如图8所示。与顺风向基底气动弯矩均方根的AIF分布规律相似,上游两侧对称建筑横向距离较大(|y/b|=1.8)时的EIF也大于其横向距离较小(|y/b|=0.9)时的结果,即上游两侧对称施扰建筑的横向间距越小,对顺风向基底峰值弯矩响应的遮挡效应越明显。对于横向间距较小(|y/b|=0.9)的情况,当x/b≥5时,EIF低于0.6且基本保持不变,表现为强遮挡效应,而当2≤x/b≤5时EIF随着串列间距x/b的减小而急剧增大,但依然表现为遮挡效应。对于横向间距较大(|y/b|=1.8)的情况,除串列间距过近(x/b≤2)表现为遮挡效应外,其他串列间距下的顺风向基底峰值弯矩响应均为放大效应,且当x/b等于5时,EIF达到最大值1.387,此时最大EIF所对应的折算风速vr为10,如图9所示。图10进一步给出了相应的广义力功率谱密度,从图10可以看到,折算风速为10时的折算频率为0.1,刚好与广义力功率谱峰值频率重合,此时受扰建筑的固有频率和施扰建筑尾流中的涡脱频率一致,即在该折算风速下发生了尾流涡激共振现象。
各串列间距比x/b下,横风向基底峰值弯矩响应干扰因子EIF的变化如图11所示。与横风向基底气动弯矩均方根AIF的分布规律相似,上游两侧对称建筑横向距离较小(|y/b|=0.9)时的EIF也远小于其横向距离较大(|y/b|=1.8)时的结果。各种x/b下,|y/b|=0.9时的EIF低于0.6且基本保持不变,表现为强遮挡效应,而当4≤x/b≤6时,|y/b|=1.8时EIF大于1,呈现放大效应,这不同于横风向基底气动力均方根AIF的结果。

图8 顺风向基底弯矩峰值响应干扰因子包络值Fig.8 EIF for the along-wind peak base moment response

图9 不同折减风速下的顺风向基底弯矩峰值响应RIFFig.9 RIF of along-wind base moment in typical work case
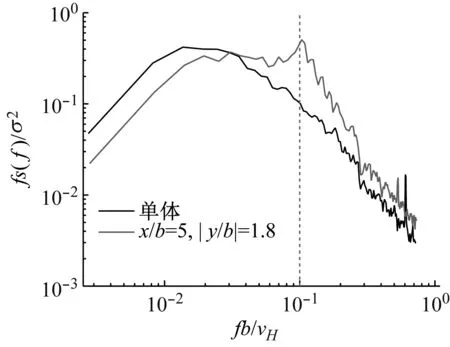
图10 顺风向广义力功率谱Fig.10 Power spectra density of the along-wind generalized force

图11 横风向基底弯矩峰值响应干扰因子包络值Fig.11 EIF for the across-wind peak base moment response
图12给出了不同串列间距比x/b下的基底峰值扭矩响应干扰因子EIF的变化规律。与基底气动扭矩均方根值AIF不同,上游两侧对称建筑横向距离较大(|y/b|=1.8)时的EIF均大于其横向距离较小(|y/b|=0.9)时的结果,且上游对称建筑横向距离较小(|y/b|=0.9)时EIF均小于1,表现为遮挡效应,但当横向距离较大(|y/b|=1.8)且串列间距为3≤x/b≤6时, EIF大于1,表现为放大效应。

图12 基底扭矩峰值响应干扰因子包络值Fig.12 EIF for the peak torsion response
3.3 顶部峰值加速度干扰因子
除了基底气动力及基底荷载响应,结构顶部加速度响应的干扰效应也不容忽视,它直接影响高层建筑的人居舒适度。结构顶部顺风向峰值加速度干扰因子EIF随串列间距比x/b的变化如图13所示。由图13可知,不同施扰建筑配置下的受扰建筑顶部顺风向峰值加速度主要起放大效应,仅当上游两侧对称建筑横向间距较小(|y/b|=0.9)且x/b=1.5和7时EIF小于1,呈现遮挡效应。当串列间距x/b=2时,上游两侧对称建筑横向间距较小(|y/b|=0.9)时的EIF大于横向间距较大(|y/b|=1.8)时的结果,除此之外,上游两侧对称施扰建筑的横向间距越小,对结构顶部峰值加速度的遮挡效应越明显。

图13 顺风向加速度峰值响应干扰因子包络值Fig.13 EIF for the peak response of along-wind acceleration
图14给出了结构顶部横风向峰值加速度干扰因子EIF随串列间距比x/b的变化。由图14可知,上游两侧对称施扰建筑的横向间距越小,对横风向峰值加速度的遮挡效应越明显。当x/b<2时,横向间距较小(|y/b|=0.9)时的EIF仅为0.52,表现为强遮挡效应,而横向间距较大(|y/b|=1.8)时的EIF接近于1,干扰效应不明显。当x/b=2时,两种横向间距下的EIF均为0.8,表现为弱遮挡效应。当x/b>2时,上游两侧对称建筑横向距离较大(|y/b|=1.8)时的EIF表现为放大效应,最大EIF为1.5,而上游两侧对称建筑横向距离较小(|y/b|=0.9)时的EIF基本保持0.8不变,呈现为遮挡效应。
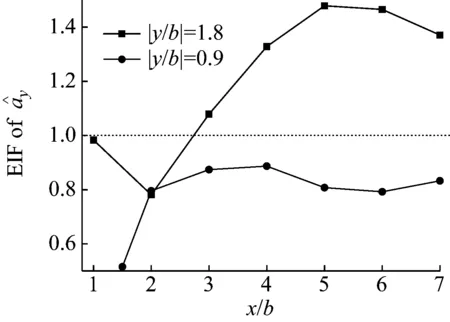
图14 横风向加速度峰值响应干扰因子包络值Fig.14 EIF for the peak response of across-wind acceleration
4 结 论
(1) 上游两侧对称建筑横向间距y/b较大时,顺风向基底脉动气动力弯矩干扰因子AIF在串列间距比x/b为4和5时表现为7%~9%的放大效应,除此之外,顺风向、横风向和扭转向的基底气动力平均值和脉动值均呈现遮挡效应。总体上,上游两侧对称建筑横向距离较大时的AIF大于其横向距离较小时的结果。
(2) 由于上游施扰建筑的尾流旋涡与下游受扰建筑的自振特性共同作用,上游两侧对称建筑横向距离较大时的顺风向、横风向、扭转向的峰值基底弯矩响应均表现不同程度的放大效应,最大干扰因子EIF分别为1.39、1.04和1.18。然而,上游两侧对称施扰建筑的横向间距较小时的顺风向、横风向和扭转向峰值基底弯矩响应依然表现为遮挡效应。
(3) 两种对称施扰建筑配置下的受扰建筑顶部顺风向峰值加速度主要起放大效应,最大干扰因子EIF达到1.77。横风向峰值加速度的最大干扰因子EIF达到1.48,但整体小于顺风向的结果。
需要指出的是,文中的受扰建筑与两施扰建筑是等宽等高的,受扰建筑的横风向效应不明显。当上游施扰建筑的截面宽度较小时,有可能出现尾流涡致振动,值得深入研究。
