板簧扭振减振器力学性质和规律研究

李嘉鹏，田中旭

（1.中煤科工集团 上海有限公司，上海 200030，2.上海海洋大学 工程学院，上海 201306）

0 引言

板簧扭振减振器因其可靠性高、减振性能优良、防腐蚀性等特点，在船用柴油机领域中广泛使用。其主要结构包括惯性块、弹性部件和阻尼部件等零件。比较早期的板簧减振器刚度计算模型是文献[1]给出的，也只能计算线性刚度，且簧片厚度须依次满足固定的厚度比。文献[2]推导出单片簧片的线性刚度，多片簧片的刚度则可视为所有簧片的刚度叠加。以上计算都是基于Euler-Bernoulli 梁模型，也没有考虑簧片与限位块的接触、簧片层间的相互作用，以及轴向和剪切变形等因素。田中旭等基于Euler-Bernoulli 梁模型[3]给出了板簧扭振减振器弯曲应力和扭转刚度的直接计算公式。目前，对渐变刚度钢板弹簧的计算方法[4-7]虽然不少，但其力学性质仍以经验公式总结和宏观力学性质测试为主要确定方法，计算精度不高，限制了减振器对工程应用的支持等多个方面。本研究基于Timoshenko 梁理论构建的高精度的力学模型，利用Matlab 软件编写基于Runge-Kutta 法的数值求解程序得到所述模型中关键参数的数值解，采用有限元进行了验证，在此基础上探讨垫片和簧片对变形和应力的影响规律。

1 减振器力学模型

采用考虑剪切变形的Timoshenko 梁理论建立减振器刚度力学模型。如若减振器设计制造合理，则簧片两端与槽底座始终接触，无冲击载荷。在构建力学模型时，减振器内外圈的相对转动可以看成簧片组与外圈接触时左端固定，簧片组与内圈接触时右端横向运动。此时，减振器扭转刚度研究的关键是簧片组两端发生相对运动，簧片受力可简化为一集中力，其集中力的方向垂直于簧片面。对于变截面的变刚度簧片来说，由于每片厚度是片长的函数，所以对于挠曲线上每一点斜率的求解较为困难。在本研究中，变形协调条件取其上下簧片的挠曲线在接触点处的坐标相等[8，9]这一假设进行求解。

减振器簧片组参数模型如图1 所示，图中黑色条状为紫铜垫片，下部为簧片1，上部为簧片2，簧片组左端固定。模型中各参数的含义见表1。

表1 板簧片参数

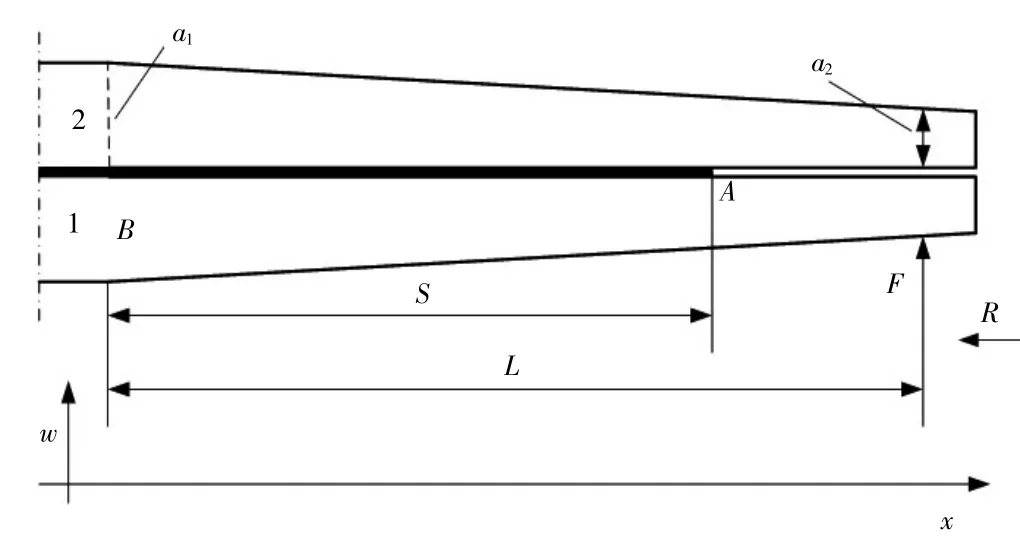
图1 簧片组参数模型

在文献[3]的基础上，考虑到边界条w1（x）|x=0=w2（x）|x=0= 0，得到两板簧片的挠度函数：

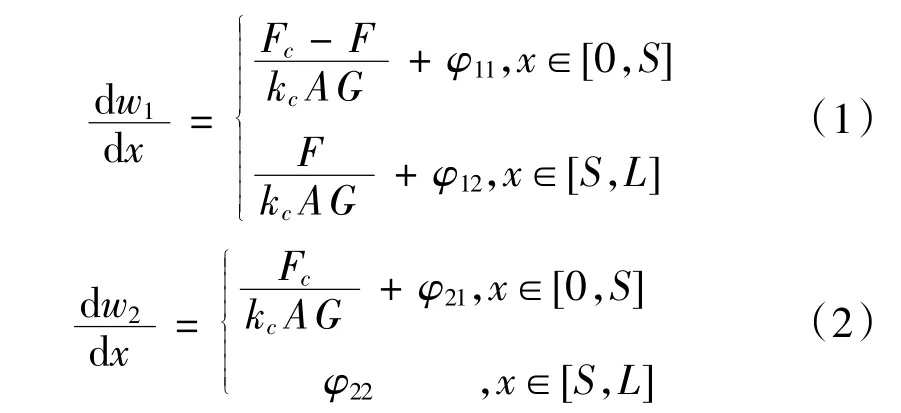
得到两板簧片的弯曲应力如式（3）和式（4）所示。

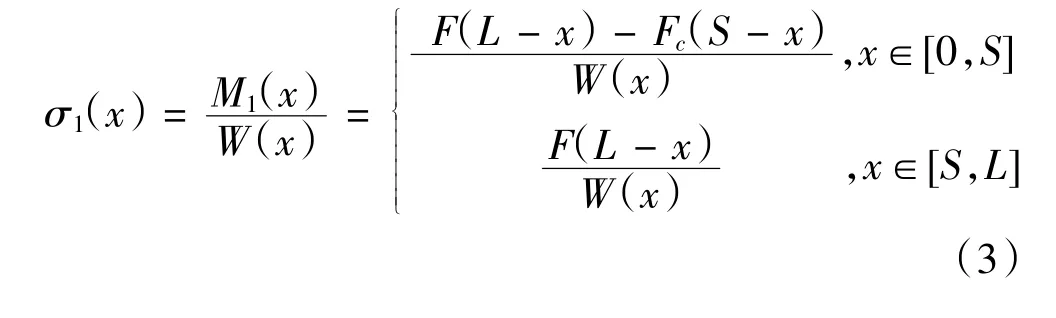
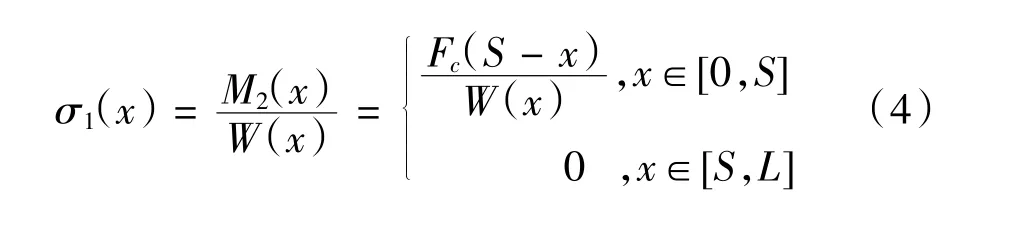
2 数值求解与验证

龙格-库塔（Runge-Kutta）法是求解数值计算中非线性常微分方程近似解的一种高精度经典方法。由于该算法精度较高，采取了抑制误差的措施，其整体截断误差为（Vx）5，通常应用于常微分方程数值求解，在工程上得到广泛应用。根据式（1）、（2），借助Matlab软件编程计算求解板簧片变形挠度的数值解，定义计算参数，分别计算5 组不同长细比板簧片末端挠度的变化结果见表2。

表2 Runge-Kutta 法和有限元法计算的挠度

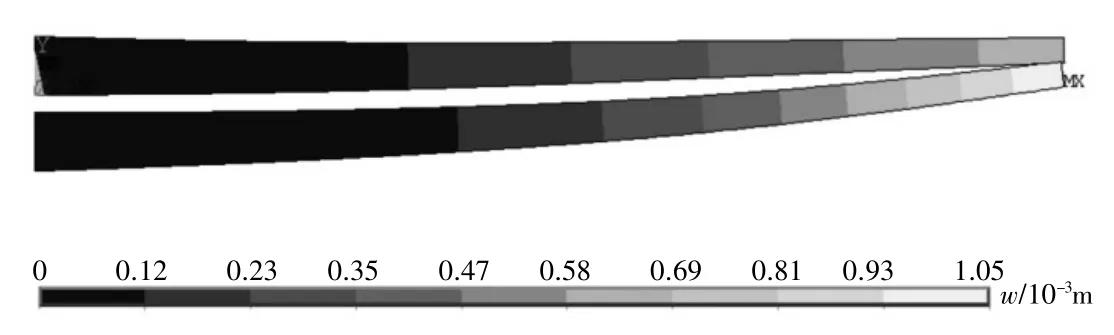
图4 有限元仿真应变云图

为了证明本研究提出的基于Timoshenko 梁理论所建立的力学模型精确解析解的可靠性和精确度，以图2 所示某型板簧片计算结果为例，利用ANSYS 进行计算分析，因板簧片的横截面大小和形状沿轴线方向不变，作用外力沿纵轴长度方向不变，故板簧片每个横截面的受力情况相同，在仿真时将板簧片分析的三维问题转化为二维平面应变问题，大大节约计算时间。建模时采用的参数如表2 所示，在板簧片垂直正方向施加集中力F= 1000 N，铜垫片末端（图1 中A处）耦合垂直方向的自由度，分别模拟板簧片长细比为8.7692、17.5385、7.0154、5.8462 以及4.3846 时板簧片1 和板簧片2 的沿Y轴变形量。图3 至图7 分别是表2 中第一至第五组数值的簧片应变云图，其中第二组至第五组数值分别是第一组簧片厚度扩大0.5 倍、1.25 倍、1.5 倍和2 倍得到的，其余参数不变。

图2 板簧片组几何模型图

图3 有限元仿真应变云图

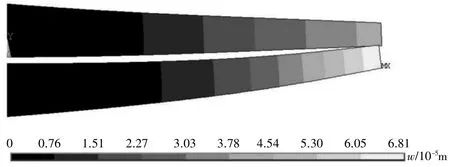
图5 有限元仿真应变云图

图6 有限元仿真应变云图

图7 有限元仿真应变云图

表2 中对集中荷载作用下减振器簧片在基于Timoshenko 梁理论构建的高精度的力学模型下四阶Runge-Kutta 数值解与有限元分析的计算结果进行比较，可以看出基于Runge-Kutta 求解方法的理论解与有限元值吻合良好。通过平面应力应变分析，以有限元分析ANSYS 的计算结果作为标准，使用Timoshenko 梁理论所建立的力学模型理论解与其比较，最大的误差才为-3.04%。从而证明了本研究求解方法对基于Timoshenko 理论建立的高精度力学模型的求解是可靠的，验证了本文计算方法的准确性。

3 减振器设计参数分析

3.1 紫铜垫片长度对变形和应力的影响

紫铜垫片作为减振器中的阻尼原件，其在减振器运行过程中虽然变形量很小（几乎可以忽略不计），但是却对簧片组结构的挠度有影响，也能改变簧片的弯曲应力分布，所以选用合适的垫片长度对于簧片组的性能发挥及强度寿命不容忽视。在研究紫铜垫片长度对变形和应力的影响之前首先要找到变形和应力最大的位置。根据式（3）和（4）编写Matlab 程序计算，绘制表2 中第一组参数簧片组的挠度曲线如图8 所示、弯曲应力分布曲线如图9 所示。从挠度图像图8 可以看到，两簧片仅在A 点接触，前文假设的计算方法正确。从图9 所示应力计算结果中可以看到，簧片1 在[0，S]范围内的应力逐渐增大，在[S，L]范围内逐渐减小到零；簧片2 在[0，S]范围内的应力逐渐减小到零，在[S，L]范围内一直为零。簧片的固定端和紫铜垫片末端为弯曲应力最大处。最大应力大小和位置受到紫铜垫片长度影响。

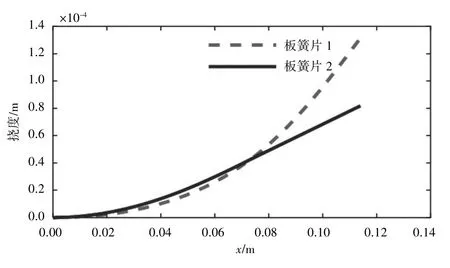
图8 板簧片挠度曲线

图9 簧片弯曲应力曲线

紫铜垫片、簧片直接关系到减振器的减振性能。为了进一步探究紫铜垫片长度对变形和应力的影响，以某型减振器为例，研究紫铜垫片长度对变形和应力的影响规律，以指导减振器的设计。从图9 可得，簧片1 在A 点和簧片2 在B 点均为簧片弯曲应力最大的地方，所以选择这两个点分析紫铜垫片长度和簧片厚度对簧片应力的影响。此时，只改变紫铜垫片长度，其余参数不变，计算10 组不同垫片长度下的簧片末端变形及弯曲应力，其结果如图10 和图11 所示。由图10 可见，随着紫铜垫片长度的增大，簧片1 末端变形减小，簧片2 末端变形增加，且越来越接近。在图11中，存在一相应的垫片长度使得板簧片1 在A 处和板簧片2 在B 处的弯曲应力值相等，且板簧片弯曲应力随着垫片长度的增大先增加后减小。

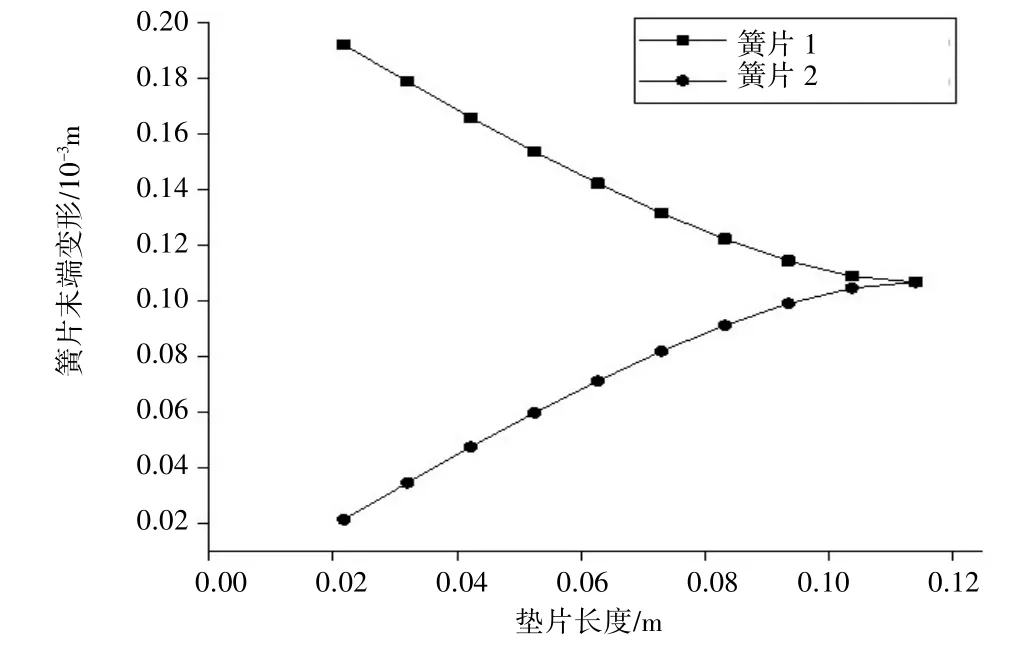
图10 垫片长度对簧片变形影响

图11 不同垫片长度下的簧片应力曲线

3.2 板簧片厚度对变形和应力的影响

板簧片作为板簧扭振减振器的核心部件，对减振器的减振性能至关重要。以某型减振器为例，研究板簧片厚度等参数对变形和应力的影响规律，以指导减振器的设计。用式（1）计算10 组不同板簧片厚度下板簧片1 末端挠度，用式（2）计算10 组不同板簧片厚度下板簧片2 末端挠度，用式（3）计算10 组不同板簧片厚度下板簧片1 在A 处的弯曲应力，用式（4）计算10组不同板簧片厚度下板簧片2 在B 处的弯曲应力。此时，只改变板簧片的厚度，其余设计参数不变。

图12 为板簧片厚度与板簧片变形关系曲线，不同板簧片厚度下的板簧片应力曲线如图13 所示。由图12 可以看出板簧片1 和板簧片2 末端变形均与板簧片厚度成负相关。图13 表明板簧片1 在A 处弯曲应力值和板簧片2 在B 处应力值随板簧片厚度的增大而显著减小。

图12 簧片厚度与簧片变形关系曲线

图13 不同板簧片厚度下的应力曲线

4 结束语

对依据Timoshenko 梁理论构建的板簧扭振减振器高精度的力学模型，本研究利用Matlab 软件编写的基于Runge-Kutta 法的数值求解程序得到了所述模型中关键参数的数值解，采用了有限元分析进行求解验证，并在此基础上探讨了力学性质的影响参数及规律，主要结论如下：

（1）基于Runge-Kutta 法的数值求解结果与有限元数值吻合较好，具有较高的分析精度。证实了本研究方法可以用于减振器的计算分析。

（2）计算并给出了减振器板簧片的挠度和弯曲应力曲线。随着紫铜垫片长度的增大，上、下两板簧片末端变形越来越接近，且板簧片1 弯曲应力最大处A和板簧片2 弯曲应力最大处B 的弯曲应力均随着垫片长度的增大先增加后减小。板簧片末端变形、板簧片1 弯曲应力最大处A 和板簧片2 弯曲应力最大处B 的弯曲应力均随板簧片厚度的增大而显著减小。

（3）在减振器的设计、制造和选型中，所提出的应力应变影响规律可起到有益的参考作用，丰富了减振器的计算方法研究。