交叉结构在面内冲压载荷作用下的损伤变形机理研究

王秀飞， 刘 昆， 沈超明， 王加夏

(江苏科技大学 船舶与海洋工程学院， 江苏 镇江 212003)

船舶碰撞搁浅事故频发，事故往往造成人员伤亡、经济损失、环境污染等灾难性后果，因此开展碰撞搁浅研究具有重要意义。在遭遇碰撞搁浅事故时，船体舷侧和船底结构中的交叉构件(舷侧纵桁与肋骨，船底纵桁与肋板)作为主要强力承载构件往往会受到面内载荷的作用而发生明显变形破坏。该类结构通常会主要承受碰撞搁浅事故载荷，需在设计分析中予以重点关注。

在船舶碰撞搁浅的相关研究中，学者们大多研究了船体外板与腹板梁在不同冲击物体下的损伤变形，并推导得到相关解析预报公式。如Wang等[1-5]对舷侧外板的变形进行了研究，提出多种解析公式预报变形阻力。傅杰等[6-7]对腹板梁在横向载荷下的变形开展了相关试验及仿真研究，并对横向载荷下腹板梁的结构抗力等进行解析预报。当交叉结构在其交叉轴线位置受到轴向压载时，交叉结构在失稳前会产生一定的压缩变形，相比于单块肋板受载情况更为复杂。针对该类问题Haris等[8-9]推导了交叉结构整体受压时的抗力计算公式，并研究了交叉结构在平面载荷下的屈曲变形过程。Hayduk等[10]分别对交叉结构、T型结构和L型结构在面载荷下的变形开展了研究，推导了平均抗力的解析计算公式。Yang等[11]开展试验研究了交叉结构和T型结构受压时的能量吸收情况以及平均抗压强度。但上述对交叉结构的研究均为面载荷，交叉结构外侧为自由边界，而当撞击船艏较小或者礁石较为尖锐时，交叉结构位置往往是受到局部载荷，故本文研究交叉结构在局部载荷下的损伤机理。

本文首先设计开展了交叉结构试件的准静态冲压试验，获得结构的损伤变形特征及承载特点，在此基础上开展相关数值仿真分析，确定交叉结构在面内载荷作用下的变形模式，运用塑性力学理论研究交叉结构受面内载荷的变形机理，得到结构变形能及抗力的解析计算公式，与试验结果比较验证。本文研究成果可用于快速评估结构抗撞性能，在船体耐撞结构设计阶段具有一定指导意义。

1 试验及仿真研究

图1为典型的碰撞搁浅场景，本文将复杂的球鼻艏结构与礁石简化为球形，研究在低速高能碰撞场景下十字交叉结构的变形损伤机理，由于在低速碰撞中材料应变率影响较小[12]，故通过对设计的交叉结构试件开展准静态冲压试验和对应的有限元仿真，分析交叉结构在面内冲压载荷下的结构响应。交叉结构受压模型如图2所示。

图1 船舶碰撞搁浅场景图Fig.1 Collision and grounding scenario of ship

图2 交叉结构受压模型Fig.2 Cross structure crushing model

1.1 试验介绍

模型试件部分由典型船底桁材与肋板的交叉位置结构简化得到，主要包括4块肋板以及面板，4块肋板焊接组成交叉结构，面板用以约束交叉结构在垂直于板面方向的位移，交叉结构与面板具体尺寸如图3所示。单块肋板尺寸为280.8 mm×300 mm×4 mm(长×高×厚)，面板尺寸为440 mm×440 mm×4 mm(长×宽×厚)。交叉结构焊接于10 mm厚的框架内部，框架顶部的四周用10#槽钢进行加强，交叉结构的面板焊接于槽钢上。整个试件材料均为船用低碳钢。球形锤头的半径为75 mm，实心锤头材料为硬度较高的GCr15(高碳铬轴承钢)，在受载情况下锤头不会产生变形。在试件上喷上银灰色油漆，并于交叉构件与面板上画上边长为20 mm的网格，以便方便观察交叉结构的变形。

1.2 试验装置及试验方案

图4为电液伺服万能试验机，该设备最大施加载荷为100 kN，移动试件将球头中心对准交叉结构中轴上，下降锤头使得锤头与面板接触，将试验机载荷值归零。试验过程中液压机以10 mm/min的恒定速率加载，锤头位移以及载荷数据由万能试验机记录，采样频率均为20 Hz。

2 有限元模型

基于图3的结构尺寸，利用非线性有限元软件ABAQUS建立有限元模型。坐标轴y沿着交叉构件的高度方向。试件模型采用四节点减缩积分壳单元(S4R)，将槽钢等效为壳单元，腰厚等效为5.3 mm，腿厚等效为8.5 mm。全局网格特征长度为10 mm。锤头刚度大且结构简单，变形忽略不计，将其设定为解析刚体。试件由四块肋板以及面板焊接为一整体，由于试件尺寸与厚度相对较小，焊缝对结构的加强显得较为明显。同时，焊缝使得结构连接处的截面变化平缓，减小受载时的应力集中现象。因此在本文的仿真中需要考虑肋板与面板以及肋板之间的焊缝。本文对于焊缝的处理方法是将焊缝处的板厚增加[13-15]，如图5所示，焊脚宽度在5～7 mm，将焊脚宽度设为6 mm，将一条焊脚截面等效为两侧板厚，在等效板厚小于焊脚截面积的情况下，经试算，两侧板厚各增加1 mm时仿真结果较为理想，即将面板与肋板焊接位置4 mm厚的板格单元设定为5 mm，交叉位置单元厚度设定为6 mm。

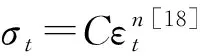
(a) 试件图

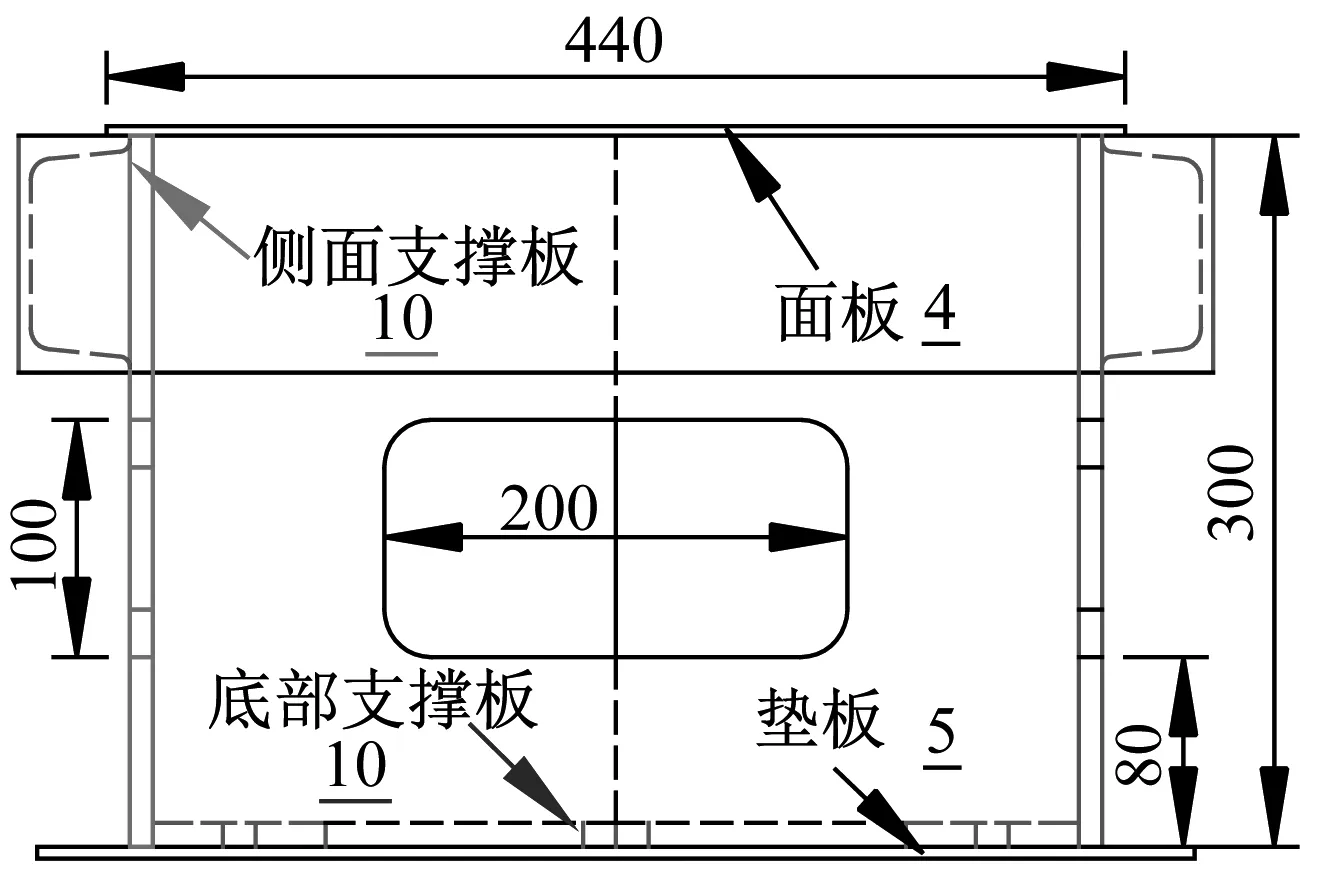
(b) 试件尺寸图图3 试件及试件尺寸图Fig.3 Specimen and geometry of specimen

图4 电液伺服万能试验机Fig.4 Electro-hydraulic servo universal testing machine

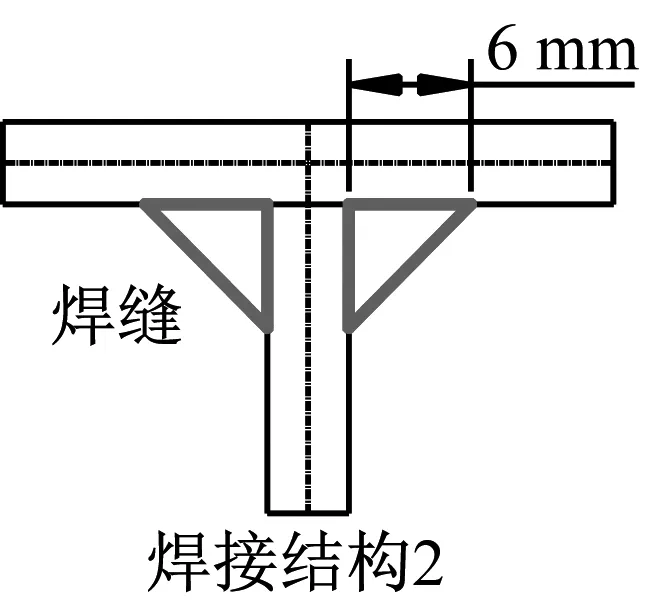
图5 焊缝处单元的等效处理Fig.5 Equivalent method of weld elements

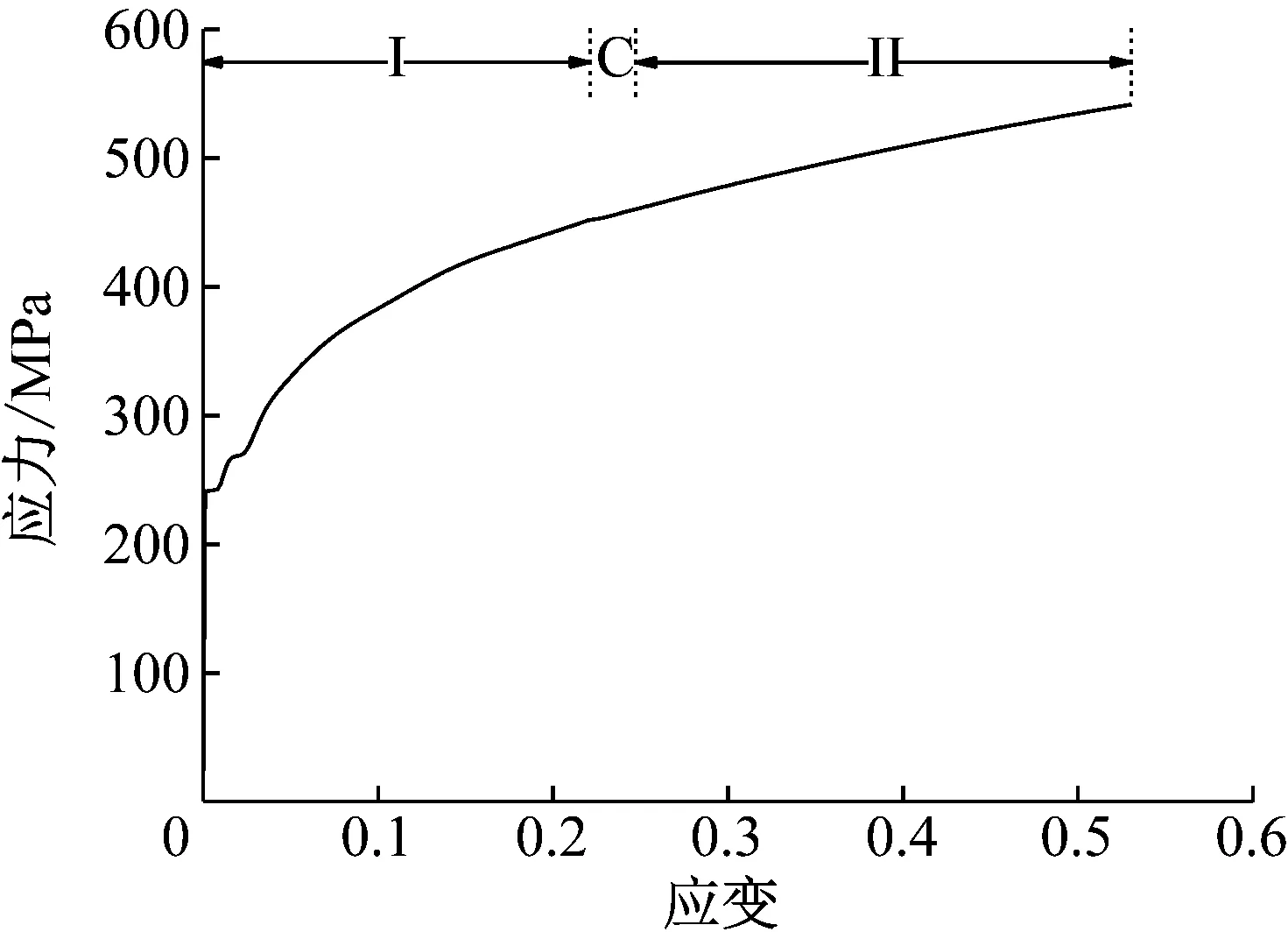
图6 组合材料关系曲线Fig.6 Combined material relationship

3 结果分析

3.1 冲压载荷

图7为试验与仿真所得的载荷撞深曲线，从图中可以看出，在I部分，试验得到的碰撞力小于仿真结果，这是由于在锤头刚接触时整个系统并未吻合。在I与II部分交替位置碰撞力达到峰值，其中仿真的碰撞力的峰值为421.12 kN，试验结果曲线中峰值为397.51 kN，误差为5.9%，II阶段为交叉结构刚刚失稳产生褶皱的阶段，碰撞力有一定的卸载，试验的卸载量小于仿真结果。II阶段末端仿真与试验的碰撞力结果一致。第III阶段，随着撞深的增加，结构抗力方向与中轴角度减小，沿着中轴方向结构抗力的分量增加，试验与仿真的结果吻合很好。

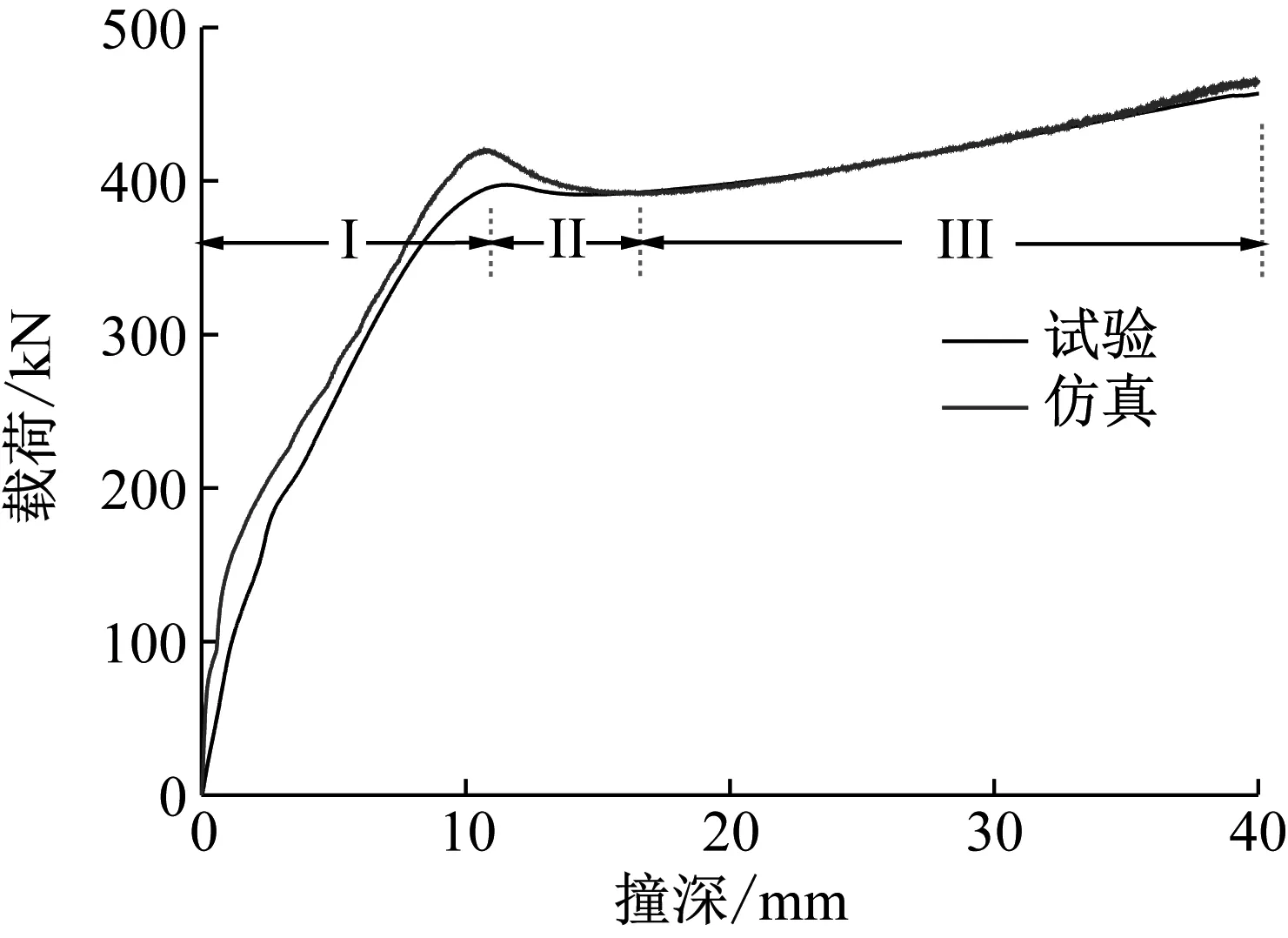
图7 试验仿真载荷-撞深曲线对比Fig.7 Comparison of impact force between test and simulation

3.2 损伤变形

图8为试验与仿真中结构的损伤变形图。从图8中可以看出，在面内冲压载荷下，面板与交叉结构均发生了很大的塑性变形。在面板与肋板的连接处，由于面板的约束，肋板仅产生向下的变形。中轴处并未产生明显的褶皱，这主要是由于交叉结构两个方向的肋板互相支撑，结构不易产生屈曲变形。由中轴向外，肋板屈曲变形程度迅速扩大，靠近约束端处不产生变形。在此阶段，单块肋板主要产生3条塑性铰，塑性铰线间肋板产生沿着其长度方向的膜拉伸变形。由于载荷与结构是对称的，试验与仿真结果均表现出4块肋板的变形近似，并关于中轴中心对称。

对比试验与仿真得到的载荷-撞深曲线以及结构的损伤变形可以看出，数值仿真较好的模拟了试验结果。因此可以使用仿真得到的肋板截面的变形过程以研究试验情况下肋板的变形过程，以便更好地分析肋板褶皱变形模式。

4 交叉构件受压变形机理

根据试验与仿真结果，对十字交叉结构变形进行如下假设:

(1) 十字交叉结构的变形分为弹性变形区域和塑性变形区域，弹性变形的能量耗散忽略不计；

(2) 由于肋板在轴向载荷下会互相支撑，相比单块肋板不易产生屈曲，故假设整个结构在碰撞初期产生局部压缩变形，当撞深达到一定距离时，交叉结构失稳产生褶皱。肋板交叉位置侧向偏移较小，不考虑其对外侧肋板变形的影响；

(3) 弹性变形区域在垂直于肋板方向的位移较小，故忽略弹性变形区域对上方褶皱变形的影响；

(4) 由于结构是对称的，并且载荷作用于结构中轴上，故四块肋板的变形近似，在解析中认为四块肋板的变形一致，并且关于中轴中心对称;

(5) 试验中锤头以恒定速率加载，并且加载速率较小，通常在实际搁浅事故中的碰撞速度较小，因此在解析方法中忽略材料应变率的影响。

(a) 中间结构变形

(b) 单块肋板变形图8 交叉结构损伤变形图Fig.8 The damage deformation of cross structure

图9 面板损伤变形Fig.9 The damage deformation of panel

由以上对试验以及仿真结果的分析和提出的假设，将交叉结构的变形分为两个阶段，并提出了一种新的肋板交叉结构面内受压的变形模式，如图10、图11所示，不同阶段变形模式的特征如下：

(1) 褶皱未形成时肋板产生局部压缩变形，受压区域范围与撞深及锤头尺寸密切相关；

(2) 褶皱从上往下三处塑性铰之间的板高比为1∶3∶2，即褶皱高度比为AB∶BC∶CD=1∶3∶2；

(3) 褶皱完成时，撞深为6H；

(4) 4块肋板的变形关于中轴中心对称。

基于提出的交叉结构受面内载荷的变形模式，运用塑性力学基本理论，推导出交叉结构在变形过程中的变形能、平均结构抗力以及瞬时结构抗力。

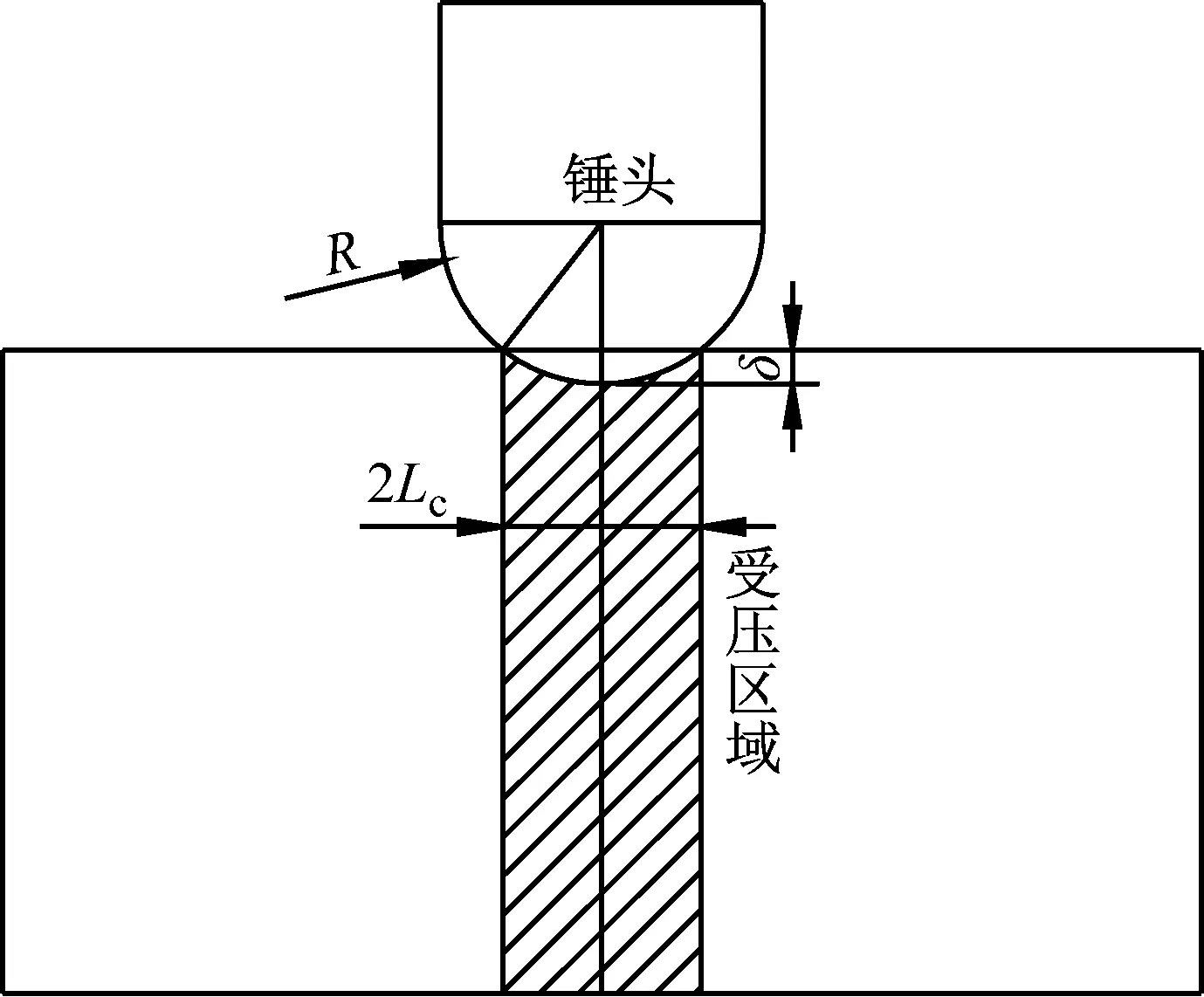
图10 局部受压阶段Fig.10 Stage of local compression

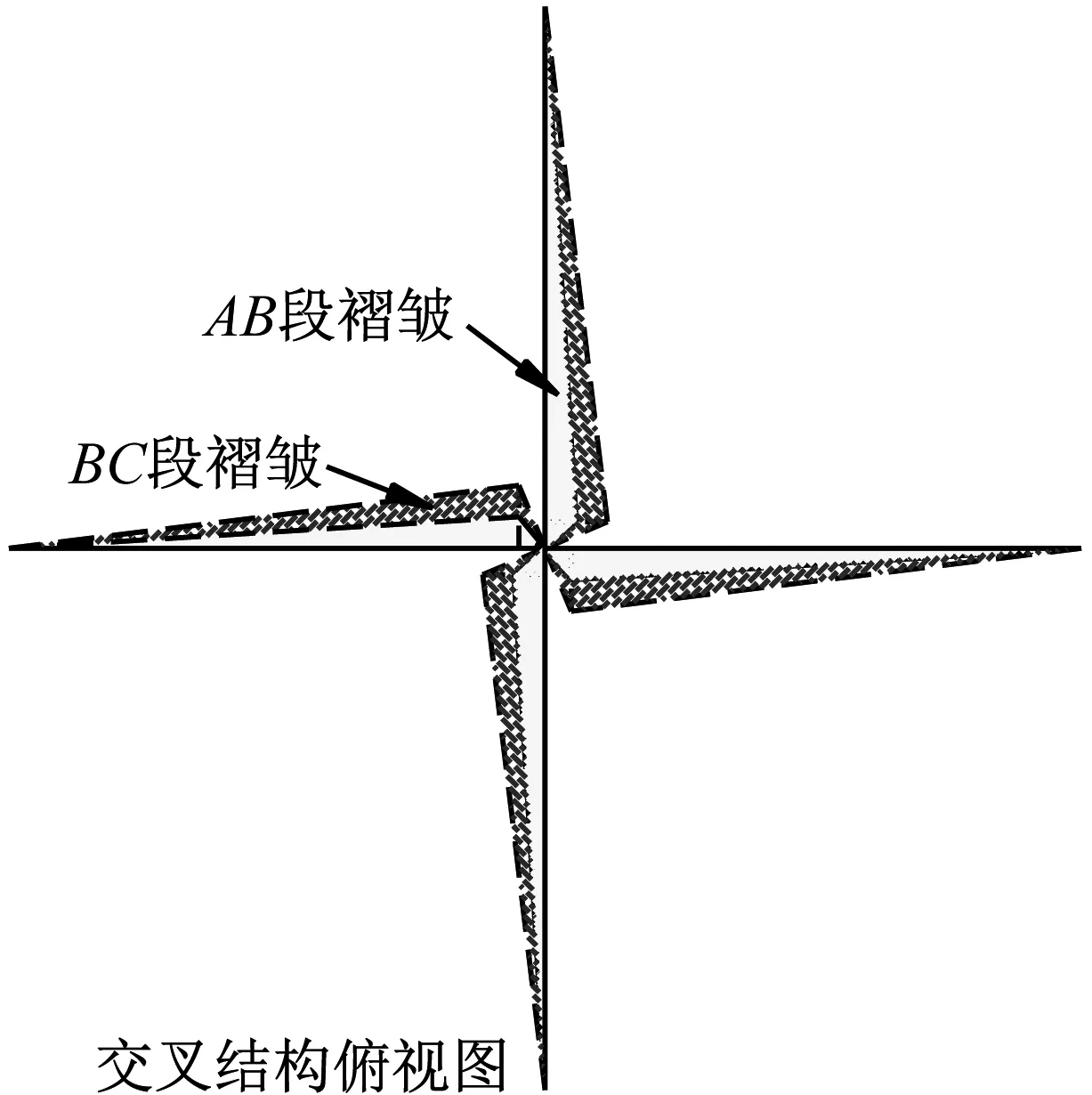
图11 肋板及交叉结构变形模式Fig.11 Deformation mode of single web girder and cross structure

4.1 交叉结构局部受压阶段

相比于单块肋板，交叉结构在面内载荷的作用下不易发生失稳，故假设在加载初期交叉结构与球头接触部分发生局部压缩变形，图10中，单块肋板受压区域长度为Lc，认为在焊缝位置在一开始时就已受压产生塑性变形。因此在第一阶段交叉结构受压的能量耗散率为

(1)

(2)

Fw,1(δ)=4σ0,wtwL+2σ0,wl2

(3)

式中：σ0,w为肋板材料的流动应力；tw表示肋板的厚度；l表示焊缝的长度，L表示肋板的长度。

4.2 褶皱形成

在褶皱形成过程中，单块肋板产生塑性变形的区域有MAB、MBC和MCD三部分，当三部分AB、BC、CD被完全压扁时褶皱完成，褶皱的总高度为6H。假设褶皱的特征高度H明显小于肋板长度L，即可认为塑性铰的长度为肋板的长度L，因此在此阶段单块肋板的塑性铰的能量耗散率为

(4)

(5)

根据图11中的几何关系，得到塑性铰转动角度与撞深的关系

δ=6H(1-cosα)

(6)

(7)

将式(7)代入式(4)，得到褶皱形成过程中单块肋板塑性铰的能量耗散率

(8)

在褶皱形成的过程中，角度α从0增加到π/2，则单块肋板塑性铰的总能量为

Eb,w,2=3πM0,wL

(9)

肋板受面内载荷时，除了产生塑性铰外还会产生膜拉伸变形。Simonsen等[22]指出，当肋板只发生沿着长度方向的拉伸变形时，才能产生最少的能量耗散。因此在解析中仅考虑沿着肋板长度方向的变形。在此情况下，膜拉伸的能量耗散率计算过程如下：

膜拉伸变形能量耗散率的计算公式为

(10)

N0,w=σ0,wtw

(11)

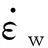
(12)

对应的应变率为

(13)

MD为塑性变形区域与弹性变形区的交界位置，此处的应变率为0，认为应变率由A～D线性变化，则塑性铰MB、MC、MD处的平均应变率分别为

(14)

(15)

(16)

计算得到褶皱的平均应变率为

(17)

将式(17)代入式(10)得到褶皱产生过程中单块肋板膜拉伸变形能量耗散率为

(18)

对上式进行积分得到褶皱被压扁时单块肋板总的能量耗散

(19)

由式(8)与式(18)得到交叉结构在变形的第二阶段的瞬时碰撞力与平均碰撞力为

(20)

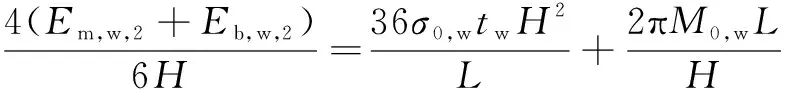
(21)

根据上限定理，在平均结构抗力最小时结构的能量耗散最小

(22)

求解得到褶皱特征高度H为

(23)

将褶皱特征高度H值代入式(20)与式(21)即得到交叉结构在褶皱产生时的瞬时结构抗力与平均结构抗力。对于试验工况，载荷加于十字交叉结构中心处，其褶皱的特征高度、瞬时结构抗力以及平均结构抗力为

(24)

对于交叉结构受压时结构抗力取式(25)中的较小值。

(25)

5 解析方法验证与讨论

通过将试验与仿真结果对本文提出的解析计算方法及进行验证，图12为试件受面内冲压载荷时的瞬时结构抗力解析计算结果与试验结果及仿真解结果的对比，从图中看出，各段的趋势吻合较好。

图12 瞬时结构抗力结果对比Fig.12 Comparison of resistance force

(1) 在碰撞初期，即曲线中I段的前部分，解析结果与仿真结果更为吻合，表明在交叉结构失稳前假设其会产生一定的压缩变形是合理的，而在I段的后半部分，解析结果的碰撞力增加减缓，数值小于仿真结果，这主要是由于解析中仅考虑了交叉结构的受压变形，而真实情况下，随着撞深的增加，产生压缩变形区域外围肋板会产生一定的膜拉伸变形，使得载荷保持继续上升。在I段，解析结果与仿真结果吻合较好。

(2) 在载荷以及变形到一定程度，交叉结构屈曲产生褶皱，载荷有所降低，从图12中的II部分看出，解析结果与试验和仿真趋势相近，并且解析中碰撞力峰值为402.67 kN，与试验及仿真结果相差很小，可见解析方法可以较好的预测该结构在面内冲压载荷下的第一次碰撞力峰值点。

(3) 图12中的III部分，随着撞深的继续增加，三种方法的载荷变化趋势一致，解析的载荷相比试验仿真结果小，主要由于产生解析中认为的膜拉伸变形区域的面积略小于实际变形区域。

6 结 论

本文以典型交叉结构为研究对象，设计并开展了带交叉结构试件的准静态冲压试验以及与之对应的数值仿真，利用塑性力学理论，对交叉结构在面内冲压载荷作用下的变形机理进行了研究。主要结论有：

(1) 由试验及仿真结果得到组成交叉结构的肋板的变形特点，提出了交叉结构受面内载荷时的变形模式，通过分析各变形阶段的能量耗散机理，获得用于预测交叉结构在面内载荷作用时的瞬时抗力、平均抗力的解析计算公式。

(2) 新的解析计算方法考虑了交叉结构较难失稳的特性，在载荷施加的初期，交叉结构两个互相垂直的肋板会互相支撑，主要在受压区域产生肋板的压缩变形。第二阶段的主要产生塑性铰以及肋板掩沿着长度方向的膜拉伸变形。

(3) 通过与仿真与试验和仿真结果的对比发现，本文提出的解析计算方法能较好的预测交叉结构在面内冲压载荷下的结构抗力，适用于船体耐撞性的初期设计与结构抗撞性能的快速评估。