超大型冷却塔龙卷风作用塔筒內表面风荷载特性研究
2021-11-17黄珑霆丁福祥
陈 旭, 黄珑霆, 丁福祥, 韩 力, 王 通, 赵 林
(1. 上海师范大学 建筑工程学院, 上海 201418; 2. 同济大学 防灾国家重点实验室, 上海 200092)
冷却塔作为火/核电厂二次高温循环水冷却的重要基础设施,被誉为世界上体量最大的空间薄壁壳体结构[1]。进入21世纪,为满足国内经济社会快速发展带来的电力高速持续增长需求,国内兴建/预研了一批超规范适用高度(165 m)[2-3]甚至刷新世界记录(200 m,德国Niederaussem电厂)[4]的火/核电超大型冷却塔。
这类兼具超高层建筑和超大跨空间结构的超大型冷却塔具有自振频率低、模态密集、阻尼比小等典型风敏感结构的特点[5-6]。传统抗风理论框架下的冷却塔结构设计研究主要基于良态气候模式,风速剖面、紊流度、湍流积分尺度、脉动风速谱等风环境参数主要针对季风、冷锋大风等气候特征[7-8]。面对全球气候变化导致龙卷风等特异风灾气候频发,受灾程度加剧的趋势[9]。若继续沿用基于传统直线式边界层气流模拟的风洞试验和结构抗风计算分析势必带来巨大的安全隐患。尤其对于核电厂而言,一旦发生龙卷风导致倒塔事故,轻则造成财产损失,重则危害核电厂运营安全甚至引发核安全事故。
风荷载作用下的冷却塔内表面风压相对外表面虽然分布较为均匀,沿高度方向差异较小,但是其数值大小对塔筒壳体稳定具有重要影响,考虑内压效应后,冷却塔整体稳定和局部稳定性下降,并随着塔高的增加下降趋势更加显著[10]。我国水工规范和德国VGB规范[11]均定义塔筒内表面风压均值取塔顶风压的-0.5倍;Kasperski等[12]的风洞试验结果也表明内压沿环向和子午向均匀分布,体型系数均值取-0.5;李鹏飞等[13]、邹云峰等[14]、柯世堂等[15-17]分别基于风洞试验和数值模拟建议了不同透风率、风雨耦合和风热耦合作用下的塔筒内压分布取值参考。然而,上述研究均基于良态气候模式。Cao等[18]基于龙卷风物理模拟器开展了龙卷风作用下的超大型冷却塔表面风荷载特性研究,结果表明:塔筒内压分布较为均匀,且内吸力远大于良态气候。上述研究可谓是超大型冷却塔龙卷风作用下的内压初探,但对于内压分布规律和内压参考取值并未深入开展讨论研究。
鉴于此,本文以某规划建设的超大型冷却塔(215 m)为研究对象,采用龙卷风物理模拟装置,开展超大型冷却塔在静态龙卷风作用下塔筒内表面风压分布规律研究,提出塔筒内压分布数学模型,量化内吸力取值,为超大型冷却塔结构抗龙卷风设计提供指导和依据。
1 工程背景与试验模型
该规划拟建的双曲线型自然通风冷却塔总高215 m,塔筒喉部标高160.610 m,塔筒下环梁标高19.594 m,塔顶中面半径51.622 m,喉部中面半径49.684 m,柱底(±0.000 m)中心半径84.634 m,塔筒底部壳体最大壁厚1.800 m,喉部附近最小壁厚0.270 m,整个塔筒由46根矩形截面一字柱支撑,原型结构尺寸如示图1所示。

图1 冷却塔原型结构示意图(m)Fig.1 The prototype of cooling tower (m)
综合考虑龙卷风物理模拟装置的阻塞率以及试验龙卷风的实际尺寸,确定该超大型冷却塔物理试验模型的几何缩尺比为1/1 500。模型采用铝锭材料并经数控铣床加工而成,确保了模型的加工精度和风洞试验必要的结构刚度(见图2)。为了使测量风压具有代表性,12个内表面测压点均匀布置在塔筒喉部位置。测压设备为PSI公司DTC Initium电子式动态压力扫描阀,采样频率为600 Hz。

图2 冷却塔试验模型Fig.2 Test model of cooling tower
2 龙卷风风场模拟
2.1 试验装置
龙卷风作用下的结构表面风荷载研究有物理试验、数值模拟和现场实测三种方法。其中,物理试验由于模拟参数可控成为目前龙卷风作用下各类机理研究应用最为广泛的工具。本试验基于同济大学防灾国家重点实验室新型龙卷风模拟器,该模拟器与美国爱荷华州立大学龙卷风模拟设备原理相似[19],属于Ward型龙卷风模拟器(见图3)。整个装置由三个同轴圆筒构成,风机和导流板布置在模拟器顶部,通过移动台架模拟自然界中龙卷风的水平迁移。试验平台采用开口式设计,升降高度H可在150~550 mm范围内自由调节,从而满足不同缩尺比的模型试验要求。

图3 同济大学龙卷风模拟器示意图(mm)Fig.3 Schematic of Tongji’s tornado vortex simulator (mm)
与之配套的龙卷风风场的测量设备是澳大利亚TFI公司的Cobra Probe三维脉动风速仪以及DPMS动态压力测量系统。该仪器的四孔探头可以测量±45°圆锥范围内2~100 m/s的三向风速和静压,测量频率为0 ~3 000 Hz。
2.2 风场特征
龙卷风作为具有三维强切变旋转效应的小尺度强烈涡旋,涡流比(Swirl ratio)是影响龙卷风涡核结构的重要参数[20],衡量切向环量与轴向动量的比值;Ward型龙卷风模拟器的涡流比按如下定义[21]
(1)
式中:r0是上升半径,与风机圆筒半径相同,为250 mm;H是试验平台的高度,本试验固定在300 mm;θV是导流板角度,试验中以10°的间隔在20°~60°范围内调节;对应五个涡流比分别为0.15、0.24、0.35、0.50和0.72。
龙卷风的风场特征可通过切向风速U、径向风速V、轴向风速W和气压降P四个参量描述。其中,切向风速是龙卷风最主要的速度分量,气压降则是造成结构破坏的最主要因素。考虑到国内F4级以上的龙卷风发生概率较小,本试验中龙卷风风场模拟的风速比设定为1/10。
图4给出了S=0.72时龙卷风切向风速U分布,其中,相对龙卷风涡核中心的距离r以及竖向高度h均由r0进行量纲归一化,可以看出:龙卷风涡核半径rc(同一高度沿r方向最大切向风速Umax的位置)沿h呈“漏斗型”分布,整个风场的最大切向速度出现在龙卷风底部靠近地表的涡核半径位置;沿r方向,切向速度呈W型分布,从涡核中心向外U先增大再减小,在rc处达到最大值。图5将五种涡流比下的U与Mulhall[22]和Spencer[23]两次龙卷风的实测值进行了对比,其中,U与r分别由Umax和rc进行量纲归一化,可以看出:试验值与实测值吻合较好,也说明了该模拟器可以较好模拟龙卷风的切向风速场。
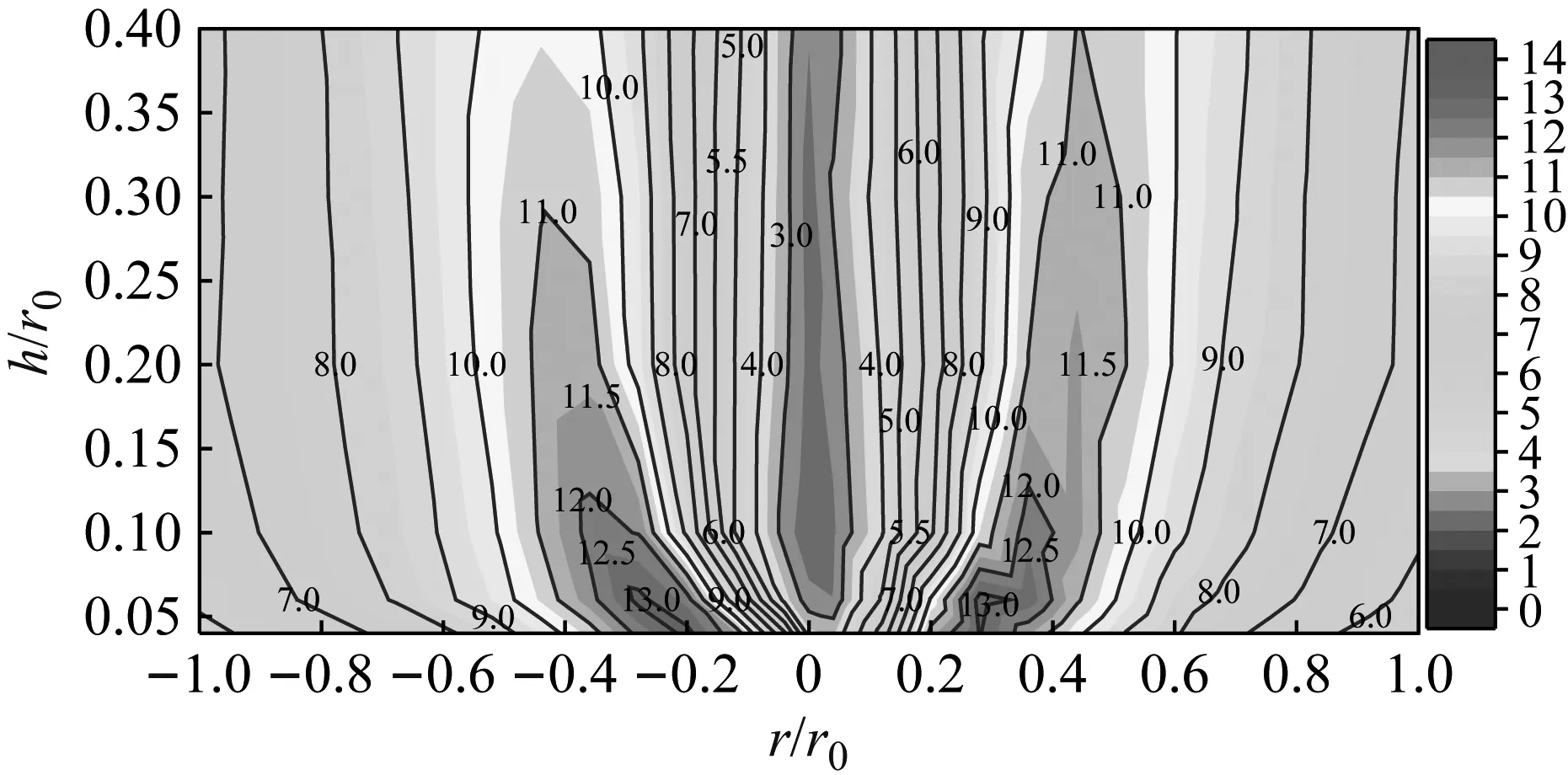
图4 龙卷风切向风速U分布Fig.4 Distribution of tangential wind velocity U
径向风速V表示龙卷风周围气流向涡核中心汇聚的速度,图6给出了S=0.72时的V分布,正/负值分别表示气流从四周流出/流向涡核中心,可以看出:涡核中心以外,气流向龙卷风中心汇聚;涡核中心附近,气流从中心向外流出;V的最大值出现在龙卷风底部靠近地表附近。
轴向风速W表示龙卷风风场中气流上升的速度,图7给出了S=0.72时的W分布,正/负值分别表示上升/下降气流,可以看出:涡核半径处上升气流速度最大,涡核半径外气流下降;由于涡流比较大,涡核中心出现了下降气流。

图5 切向风速试验值与实测值对比Fig.5 Comparison of U in the test with those fromfield measurements

图6 龙卷风径向风速V分布Fig.6 Distribution of radial wind velocity V

图7 龙卷风轴向风速W分布Fig.7 Distribution of axial wind velocity W
为了显示龙卷风二维涡核结构,将V和W进行矢量求和,图8分别给出了低(S=0.15)、高(S=0.72)两种涡流比下的结果,可以看出:低涡流比下,龙卷风涡核结构中只有上升气流,为单核;高涡流比下,涡核中心出现了明显的下降气流,为双核龙卷风;因此,涡流比增大,龙卷风从单核向双核转变。同时,涡核中心两侧的空气流速不对称,说明了龙卷风涡核结构的不对称。
图9给出了S=0.72时的气压降P分布,可以看出:涡核中心气压降最大,距离涡核中心越远,气压降越小。将五种涡流比下的气压降与Rankine理论模型[24]以及Manchester实测值[25]进行对比(见图10),分布形式上试验值与实测值吻合较好,均为非对称V型分布,Rankine模型则为对称V型分布,数值上试验值与Rankine模型较为接近,但与实测值存在一定偏差,这是由于试验中无法再现某个特定的龙卷风。

(a) S=0.15

图9 龙卷风气压降W分布Fig.9 Distribution of pressure drop accompanying a tornado W
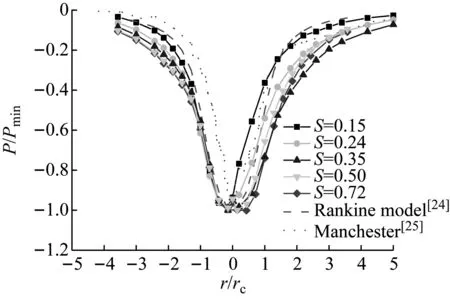
图10 气压降试验值、理论值与实测值对比Fig.10 Comparison of P in the test with results from thetheoretical model and the field measurement
从对龙卷风U、V、W和P的模拟结果来看,该龙卷风模拟器可以较好地模拟自然界中真实龙卷风的一般风场特征。
3 内压试验结果与讨论
3.1 参数定义
与传统大气边界层风洞试验中风压数据处理方式相同,采用风压系数对龙卷风作用下的内表面风荷载进行无量纲化处理,其定义如下
(2)
式中:CP是无量纲风压系数;P是环向角度θ下风压时程;P∞是远离龙卷风风场的静压;ρair是空气密度;Umax是涡核半径处的最大切向速度。
极值风压采用考虑测点间相关性的定义方式,公式如下
μE=μP+ρ*g*σP
(3)
式中:μP、σP和μE分别是内压系数的均值、脉动值和极值;g是Davenport峰值因子[26];ρ是内压测点间的相关系数。
冷却塔中心与龙卷风涡核中心相对距离rm的定义如图11所示;其中,rm的正/负值分别表示龙卷风位于冷却塔左/右侧,1~12分别为塔筒喉部12个内压测点的环向位置。

图11 冷却塔与龙卷风相对距离Fig.11 Relative distance between cooling tower and tornado
3.2 分布特征
图12给出了S=0.72时冷却塔相对龙卷风涡核中心不同距离的环向内压分布,其中,rm由rc进行量纲归一化;可以看出:内压均值和脉动值沿环向分布均匀,当冷却塔位于龙卷风涡核中心时(rm/rc=0),内吸力最大,内压的脉动性也最强,随着冷却塔逐渐远离龙卷风涡核中心,内吸力逐渐减小;同时,与平均值相比,内压脉动值较小,说明内压时程的波动性较小;内压的分布特征说明了其受塔筒外部龙卷风三维风场的影响较小,主要受龙卷风气压降的影响。
图13给出了不同涡流比龙卷风下的冷却塔内压分布,其中,内压均值/脉动值是对相同rm处环向12个内压测点平均/脉动内压系数取算术平均。从均值分布来看:当冷却塔位于龙卷风涡核半径内(0≤|rm/rc| ≤1),内压系数绝对值随着S的增大而减小,即S越大,内吸力越小;当冷却塔位于龙卷风涡核半径以外(|rm/rc| >1),内压系数绝对值随着S的增大而增大,即S越大,内吸力越越大。从脉动值分布来看:0≤|rm/rc| ≤1的内压脉动性最大,|rm/rc| >1的内压脉动性迅速减小,同时,低涡流比龙卷风作用下的内压脉动性大于高涡流比。

(a) 内压均值

(b) 内压脉动值图12 冷却塔内压环向分布Fig.12 Distributions of inner pressure coefficients oncooling tower in the circumferential direction
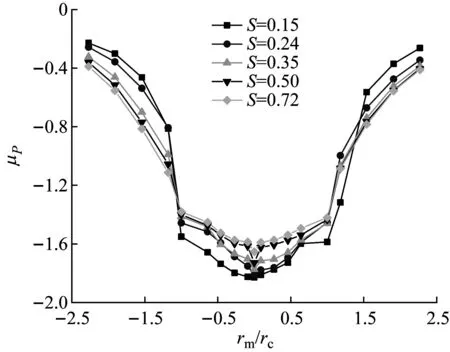
(a) 内压均值

(b) 内压脉动值图13 不同龙卷风涡流比下冷却塔内压分布Fig.13 Distributions of inner pressure coefficients oncooling tower with swirl ratios
从S=0.72时所有内压测点与1号测压点间的环向相关系数分布来看(见图14),随着测压点沿环向逐渐远离1号点,相关性逐渐减弱,但是即便是与1号点相背离的7号测压点,两者之间的相关系数也约0.90,因此,可以说龙卷风作用下的环向内压间呈强相关性。

图14 内压测点间相关系数分布Fig.14 Distributions of correlation coefficients amonginner pressure taps
图15给出了五种涡流比下相关系数随冷却塔与龙卷风相对距离的变化趋势,其中,每个rm处的相关系数是对环向12个测点相关系数的算术平均值。随着rm的增大,内压间的相关性先增大再减小,在涡核半径处(|rm/rc|=1)相关性最强;同时,高涡流比下的内压相关性要小于低涡流比。

图15 不同龙卷风涡流比下冷却塔内压相关性Fig.15 Correlation coefficients of inner pressures withswirl ratios
图16和图17分别给出了峰值因子沿环向的分布以及五种涡流比下峰值因子随冷却塔相对位置的变化,可以看出:g沿环向均匀分布,不同S下,数值介于3.6~4.0之间;当冷却塔位于龙卷风涡核中心(|rm/rc|=0)以及涡核半径处(|rm/rc|=1),g最小;低涡流比龙卷风下的g要小于高涡流比下。
由于构成内压极值μE的均值μP、脉动值σP、峰值因子g以及相关系数ρ均沿环向均匀分布,因此,μE也沿环向均匀分布(见图18);同时,μE在|rm/rc|=0绝对值最大,即涡核中心的冷却塔内吸力极值最大,随着|rm/rc|逐渐增大,μE绝对值逐渐减小,当|rm/rc|>1后,μE绝对值迅速减小;并且,当0≤|rm/rc|≤1时,μE绝对值随着S增大而减小,而|rm/rc|>1后,μE绝对值随着S增大而增大(见图19)。
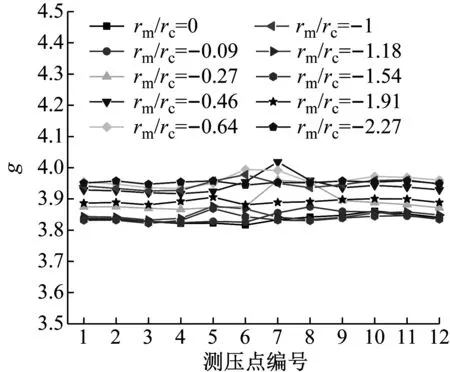
图16 内压峰值因子分布Fig.16 Distributions of peak factors of inner pressures
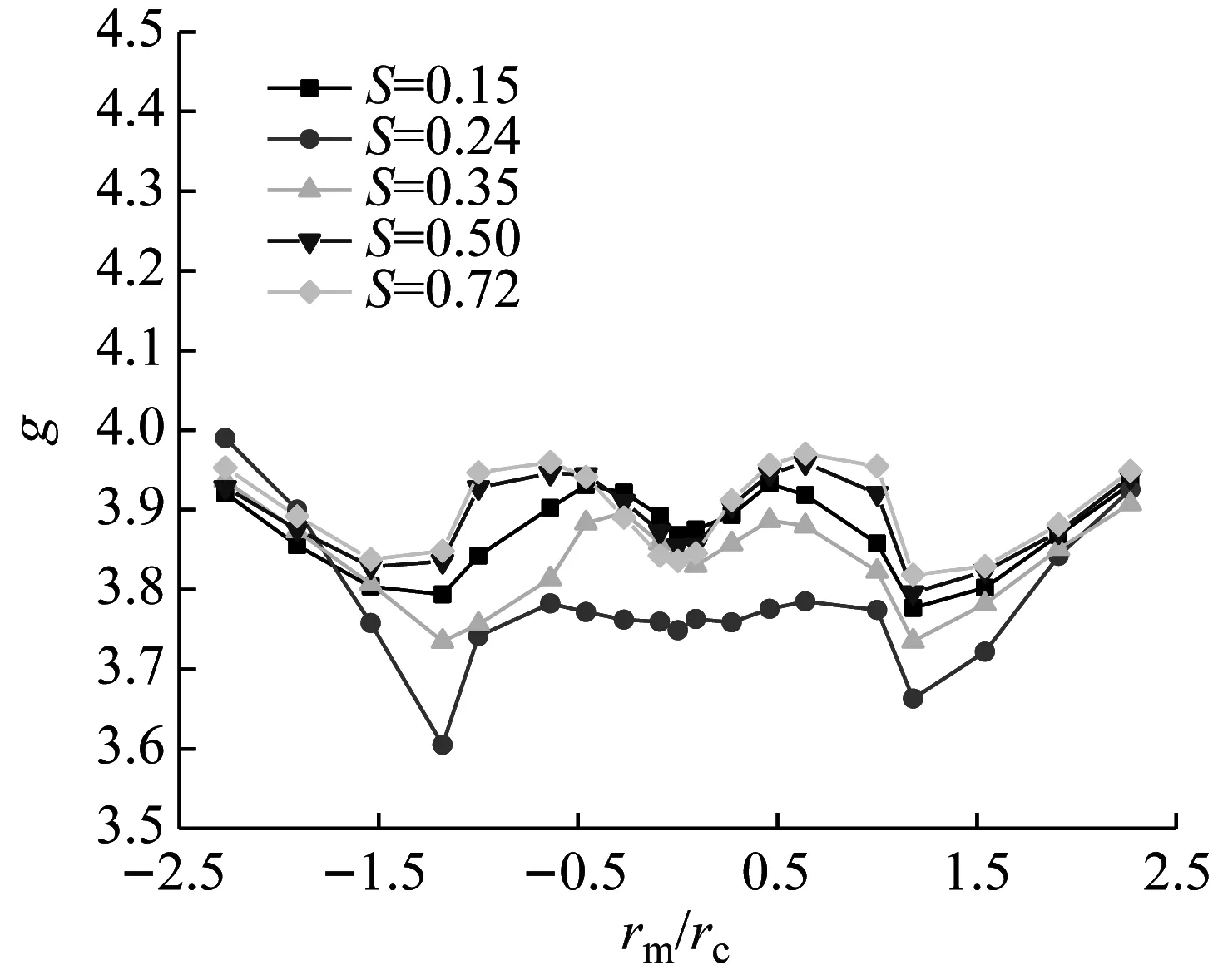
图17 不同龙卷风涡流比下冷却塔内压峰值因子Fig.17 Peak factors of internal pressures with swirl ratios

图18 内压极值分布Fig.18 Distributions of peak values of inner pressures
3.3 内压模型
从不同涡流比下冷却塔内表面风压随龙卷风与冷却塔相对位置的变化趋势(见图13(a)、图19)可以看出,其分布形式与龙卷风气压降的分布形式相似(见图10),服从Rankine模型的V型分布。

图19 不同龙卷风涡流比下冷却塔内压极值Fig.19 Peak values of inner pressures with swirl ratios
基于Rankine二维涡旋模型的龙卷风气压降[27]表述如下

(4)
式中:P(r)是距离龙卷风涡核中心位置r处的龙卷风气压降;Pmin是龙卷风涡核中心的气压降;rc是龙卷风涡核半径。
由于龙卷风作用下的冷却塔内压主要受气压降的影响,将内压均值表述成与Rankine模型相似的形式,公式如下
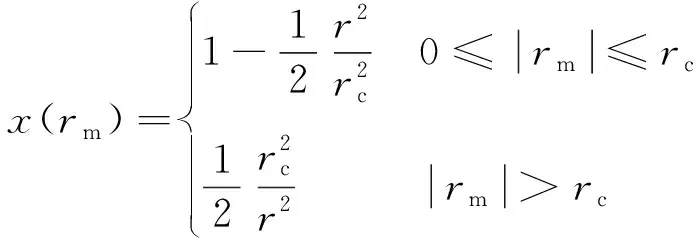
(5)
(6)
式中:μP(rm)是距离龙卷风涡核中心rm位置处的冷却塔内压均值;μmin是处于龙卷风涡核中心位置的冷却塔内压均值。
图20给出了S=0.72时y与x的拟合关系式,冷却塔内压随其相对龙卷风的位置呈对数分布关系,并且试验值与拟合值吻合较好(见图21)。表1给出了五种涡流比下的内压拟合关系,可以看出:不同涡流比下,冷却塔内压与其相对龙卷风的距离均满足对数分布关系,其中拟合关系式中的常数项均为1,对数项因子为0.32~0.40。
实际工程设计中一般采用最不利荷载,对五种龙卷风涡流比下的冷却塔内压均值取最不利分布,并采用上述模型进行拟合(见图22);其中,冷却塔位于龙卷风涡核中心的内压均值取-1.82,对数拟合公式的常数项和对数项因子分别取1和0.34(见式(7))。与水工规范中定义的良态气候下冷却塔内压均值-0.5相比,龙卷风产生的内吸力大于良态气候,这将不利于塔筒局部风致稳定性。
μP(rm)=

(7)

图20 内压分布拟合关系Fig.20 Fitting curve of inner pressure distributions

图21 内压试验值与拟合值对比Fig.21 Comparison between experimental values and fitting values

表1 五种涡流比下的内压拟合曲线Tab.1 Fitting curves of inner pressure with five swirl ratios
4 结 论
本文采用龙卷风物理模拟装置开展了某215 m超大型冷却塔内表面风荷载特性研究,探讨了不同涡流比下的塔筒内压分布特征,提出了龙卷风作用下的塔筒内压分布数学模型,主要结论如下:

图22 最不利内压值拟合Fig.22 Fitting of the most adverse inner pressures
(1) 龙卷风作用下的冷却塔内表面风压受龙卷风气压降和塔筒外部龙卷风三维风场共同作用,其中,气压降是影响内压大小和分布的最主要因素。
(2) 龙卷风作用下的塔筒内压呈均匀分布、环向强相关的负压,即表现为吸力;内吸力随龙卷风涡核半径内涡流比的减小以及塔心至涡心间距的减小而增大,即冷却塔位于低涡流比下的龙卷风涡核中心时所受内吸力最大。
(3) 龙卷风作用下的塔筒内压服从Rankine涡旋模型的V型分布,可以定量表示为与塔筒和龙卷风相对位置有关的对数模型;最不利工况下龙卷风涡核中心的塔筒内压均值取-1.82,内吸力大于水工规范定义的良态气候;内压对数拟合公式中的常数项和对数项因子分别取1和0.34。
