针对齿轮箱阶次噪声问题的多体仿真

2021-11-16张剑

传动技术 2021年3期

张剑

(上海汽车集团股份有限公司商用车技术中心，上海 200438)

0 前言

齿轮系统噪声声源主要有：齿轮系统本身轮齿啮合的动态激励、原动机(发动机、电动机等)的振动以及工作机构的振动和负载变化等[1]。齿轮啮合产生的齿轮力阶次脉动，通过齿轮轴及轴承传递到齿轮箱壳体，引起壳体振动，对外辐射出噪声，严重影响整车品质及用户体验。因此有必要分析齿轮箱噪声产生机理及影响因素，在设计初期，通过减振降噪设计尽量避免可能产生的NVH问题。在设计后期，通过工程手段有效控制齿轮箱振动，降低噪声水平，提升整车舒适性。

本文基于齿轮箱多体动力学建模，进行全转速域内齿轮箱动力学仿真分析，特别是关注轴承力及关键区域壳体表面振动速度响应。通过相应的车内振动噪声试验，比较壳体表面振动频谱与噪声频谱数据，验证单啮合阶次下共振频率的准确性。也为通过激励源“减振”方法，达到齿轮箱“降噪”目标提供理论依据。

1 机械振动理论基础

系统受到外界持续的激励作用而“被迫地”产生振动，其振动特性除取决于系统本身的特性外，还取决于激励的特性[2]。单自由度有阻尼机械系统在简谐激励力作用下的强迫振动运动微分方程为：

(1)

(2)

微分方程式(2)是一个二阶线性常系数非齐次微分方程式。它的通解可以用二阶线性常系数齐次微分方程式的通解x1(t)和方程式(2)特解x2(t)之和来表示：

x=x1(t)+x2(t)

(3)

式中，x1(t)代表阻尼系统的自由振动，在小阻尼的情况下，这是一个衰减振动，在开始振动后某一较短的时间内有意义，随着时间的增加，它将衰减下去[2]。当仅研究受迫振动中的持续的等幅振动时，可以略去x1(t)。

x2(t)表示阻尼系统中的受迫振动，称为系统的稳态解。从微分方程式非齐次项是正弦函数这一性质，可知特解的形式也是正弦函数，它的频率与激振频率相同。因此可设特解为：

x2(t)=Bsin(ωt-ψ)

(4)

式中B—受迫振动的振幅；Ψ—位移落后于激振力的相位角。

将x2(t)及其一阶、二阶导数代入方程式(2)中，可解出B与Ψ为：

(5)

(6)

(7)

(8)

从式(3)、式(7)及式(8)可以看出，具有粘性阻尼的系统受到简谐激振力作用时，受迫振动也是一个简谐运动，其频率和激振频率ω相同，振幅B、相位角Ψ取决于系统本身的性质(质量m、弹簧刚度k、黏性阻尼系数r)和激振力的性质(激振力幅值F0、频率ω)，与初始条件无关[2]。

2 齿轮箱多体建模

2.1 齿轮箱构造

电驱总成由驱动电机、控制器及齿轮箱组成，采用三点悬置与车身连接。齿轮箱总成由前、后壳体、齿轴系及差速器组成，总成结构如图1所示。齿轮箱后壳体大断面通过周向法兰与驱动电机连接，后壳体输出轴侧、前壳体输入轴侧通过悬置支架连接。齿轴系结构如图2所示，为两级斜齿轮减速机构。输入轴为独立齿轮轴结构，中间轴由齿轮轴与中间轴大齿轮组成，输出轴齿轮与差速器壳体通过周向法兰连接，齿轮设计参数如表1所示。

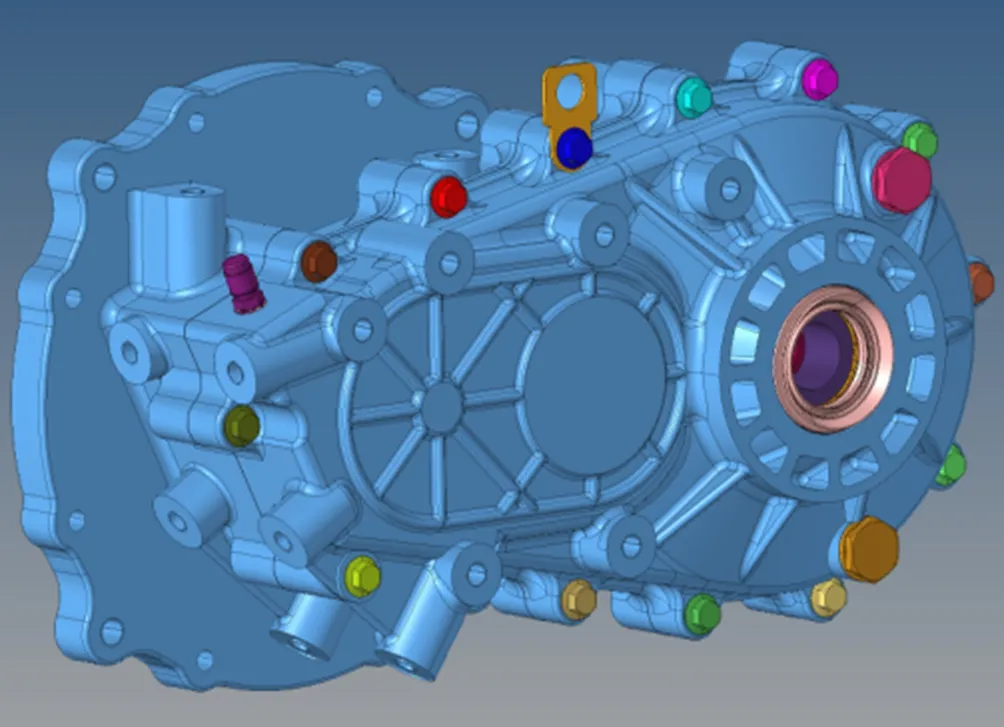
图1 齿轮箱总成Fig.1 Gearbox

图2 齿轴系Fig.2 Gear train

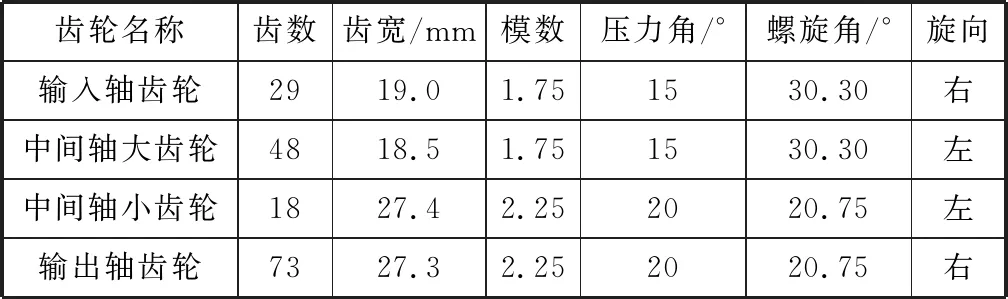
表1 齿轮设计参数Tab.1 Gear design parameters

2.2 多刚柔耦合体

多体建模采用刚柔耦合法，考虑到壳体结构表面振动及弹性变形，建立柔性体差速器壳体、齿轮箱壳体如图3所示。采用四面体网格划分，前后壳体连接螺栓采用rbe2单元刚性简化，轴承中心处同样采用rbe2单元与轴承座表面刚性连接。提取壳体前50阶约束模态，基于振型叠加法计算柔性体响应。齿轮轴采用刚性体建模，导入高质量三维数模，刚体之间定义接触。轴承简化为线性轴承，定义三个方向刚度及随转速变化的黏性阻尼。基于齿轮设计参数，定义3D齿轮。齿轮箱刚柔耦合多体动力学模型如图4所示。

图3 壳体有限元模型Fig.3 Housing FEA model

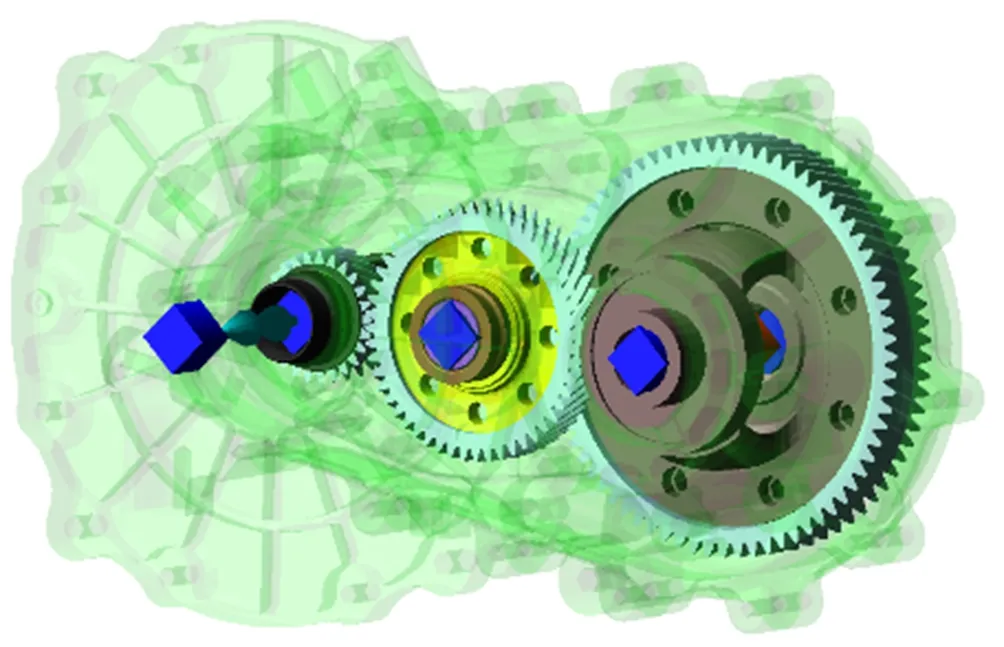
图4 刚柔耦合多体模型Fig.4 MBD model with rigid and flex body

2.3 载荷及边界条件

参考电驱总成在整车上的悬置布置方式，约束齿轮箱后壳体大断面、后壳体输出轴侧、前壳体输入轴侧的悬置螺栓孔。齿轮箱输入轴施加转速，5.6 s内转速从0 r/min恒定加速度提升至7 000 r/min，如图5所示。根据电机输出外特性扭矩和齿轮箱理论速比，反算出齿轮箱输出轴扭矩，加载到齿轮箱输出轴，如图6所示。

图5 电机输入转速Fig.5 Motor rpm

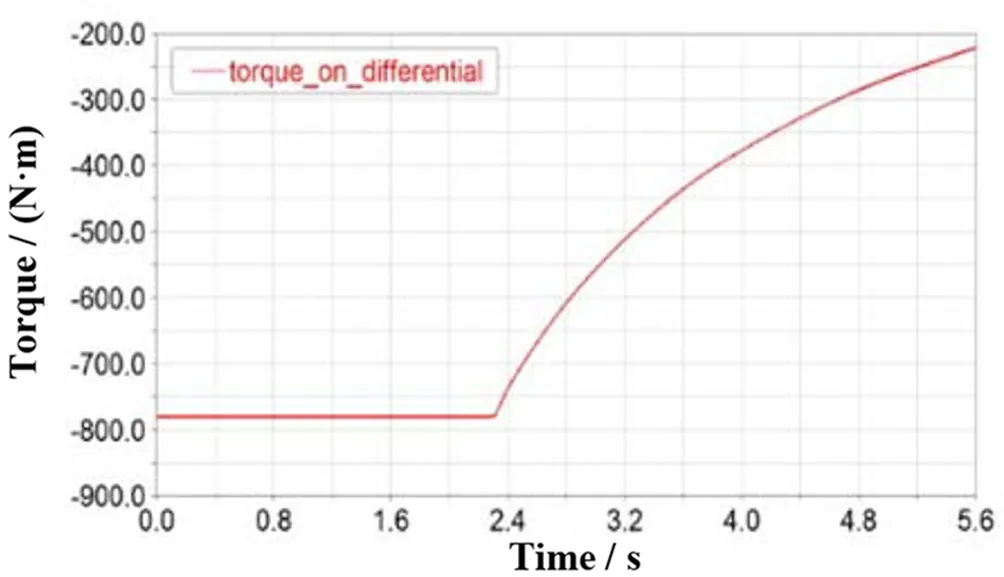
图6 差速器输出扭矩Fig.6 Differential torque

3 齿轮箱多体动力学分析

3.1 轴承力

轴承力由齿轮啮合产生，取0.4 s到4.8 s时间域内，即500 r/min到6 000 r/min转速内轴承力数据进行快速傅里叶变换。显示频域内11阶、29阶齿轮啮合阶次轴承力幅值，及对应的啮合阶次二倍频22阶、58阶轴承力。输入轴对应的轴承轴向力、左右轴承径向力如图7所示，中间轴对应的轴承力如图8所示，输出轴对应的轴承轴力如图9所示。

图7 输入轴轴向、径向左、径向右轴承力Fig.7 Input shaft bearing force at axial, radial left and radial right

图8 中间轴轴向、径向左、径向右轴承力Fig.8 Middle shaft bearing force at axial, radial left and radial right

图9 输出轴轴向、径向左、径向右轴承力Fig.9 Output shaft bearing force at axial, radial left and radial right

与扭矩传递方向相关，输入轴及中间轴轴向力同向，输出轴轴向力反向。由于速比逐级增大，扭矩及轴承力逐级增大，且径向轴承力较大，轴向轴承力较小。根据齿数计算，一级齿轮啮合阶次29阶，二级齿轮啮合阶次11阶，因而输入轴轴承力主要受29阶齿轮啮合影响，中间轴轴承力受29阶及11阶共同影响，输出轴轴承力主要受11阶影响。

3.2 振动速度

辐射噪声由壳体表面振动引起，近场声压与壳体有效振动面积上的振动烈度强相关。壳体关键区域振动速度如图10所示，最大振动速度出现在前壳体中间轴与输出轴连接位置，与轴承力分析中，中间轴及输出轴轴承力较大，输入轴轴承力较小相吻合。

图10 关键区域振动速度Fig.10 Vibration velocity of key area

壳体关键振动区域在阶次轴承力激励下，产生共振响应。壳体受迫振动过程中，无约束的大平面且薄壁结构对辐射噪声的贡献度最大。仿真过程中，在柔性体壳体表面标记节点，输出时域内法向振动速度。由于输入轴轴承力幅值较小，仅标记中间轴及输出轴。节点1011对应中间轴区域，1005、1010对应输出轴区域，如图11所示。

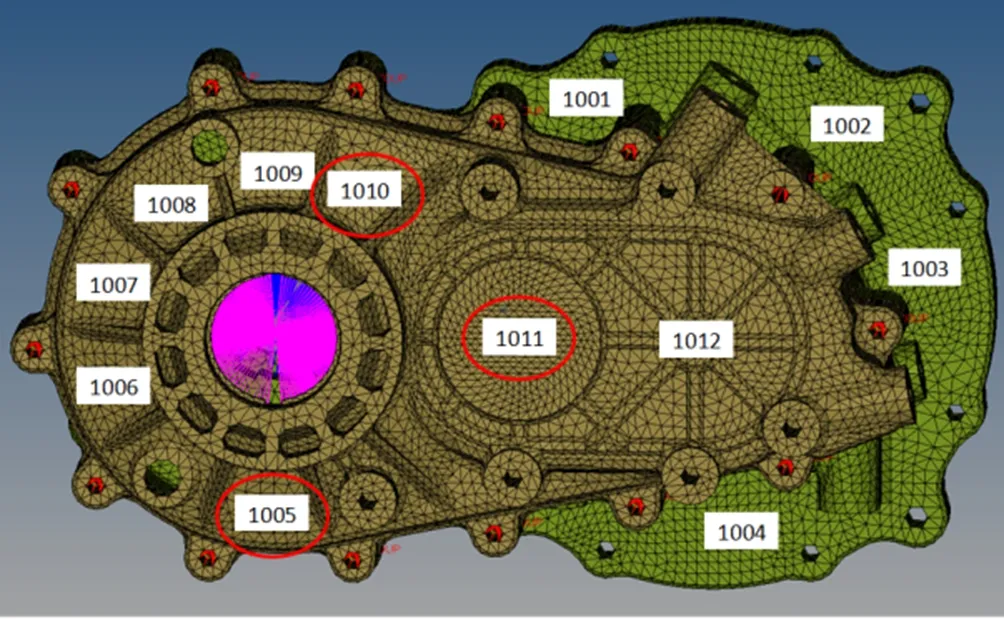
图11 壳体表面振动关键区域Fig.11 Key area of housing surface vibration

4 车内噪声试验验证

将关键振动区域点1005、1010、1011时域内振动速度进行傅里叶变换，得到振动速度频谱如图12所示。1005、1010点11阶振动速度在2.1 s(2 625 r/min)时有最大振幅，1011点29阶振动速度在1.75 s(2 150 r/min)时有最大振幅。车内噪声测试频谱如图13所示，其中11阶共振峰值转速2 800 r/min，29阶共振峰值转速2 400 r/min。

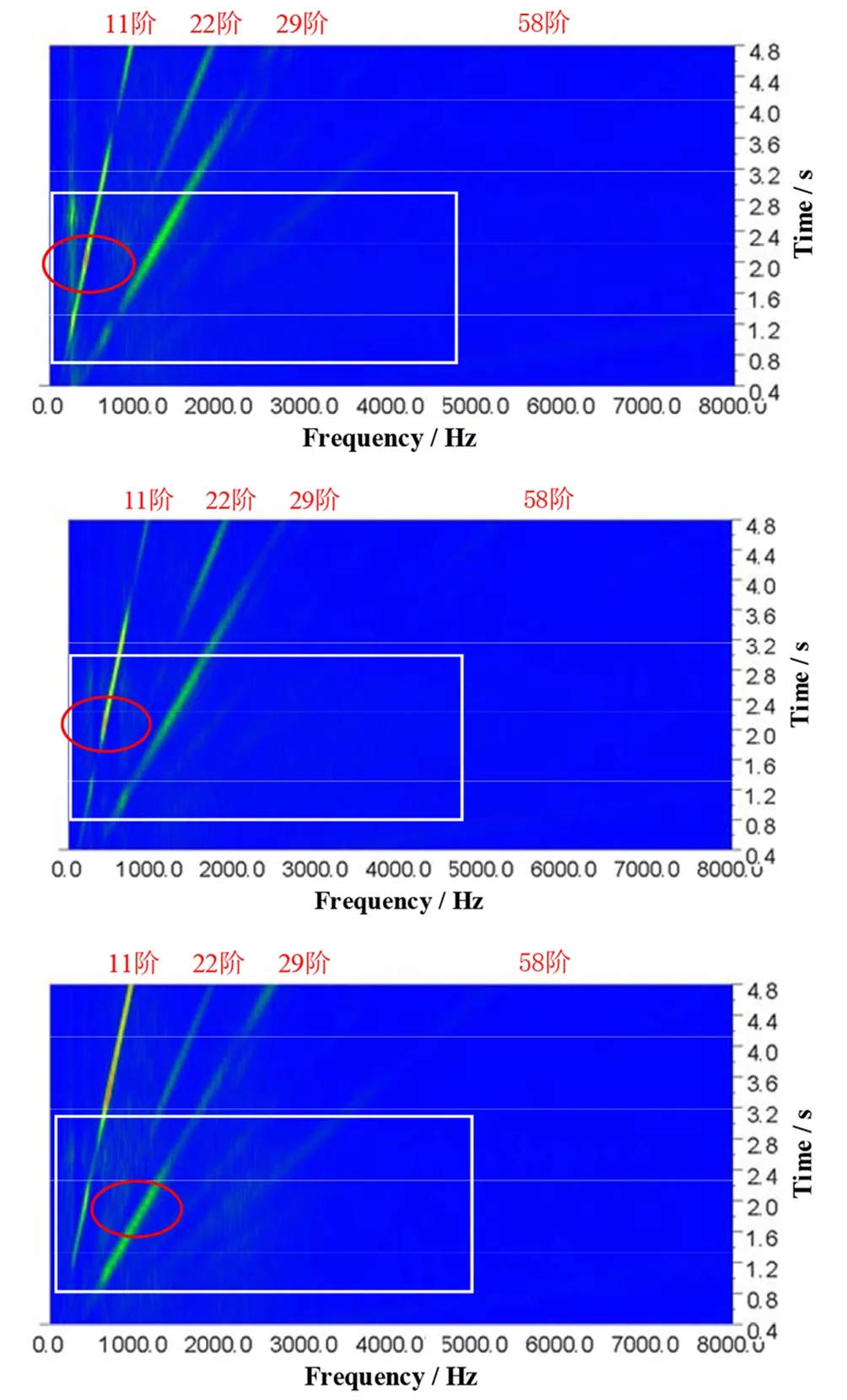
图12 节点1005、1010、1011振动速度Fig.12 Vibration velocity of node 1005,1010,1011

图13 车内噪声测试Fig.13 Vehicle interior noise measurement

振动仿真与噪声测试共振频率对比如表2所示，11阶对应的壳体共振频率481 Hz，噪声测试体现的共振频率513 Hz，相差-6.3%，29阶对应的壳体共振频率1 039 Hz，噪声测试体现的共振频率1 160 Hz，相差-10.4%。仿真结果显示出较高的精度，表明振动仿真对于噪声测试的共振频率有较强的指向性。