初中数学易错题的纠正措施例谈

宋春莹 刘玉梅

摘要：近几年的教育教学理念不断更新：核心素养、深度教学、 大单元教学……

层出不穷，但这些理念的本质都是让教师跳出教材的僵化使用、跳出中考题型的束缚，是在提倡教育是为了学生的发展而教，而不是为了应考而教。数学错题纠正的过程，实际上就是纠正一种习惯或者一种思维的过程，数学是培养学生思维的学科，数学教师需要不断的优化教學方法，研究出更好的教学案例，让教学研究成为教师教育生涯的养料，让教师在学生的错误土壤中浇灌出智慧之花。

关键词：易错题;策略;数学思;案例;纠错;方法;审题

初中数学是一门对逻辑性和推理性要求较高的课程，由于这一学科的抽象性和严谨性，学生就会经常出现各种不同的错误，致使教师最复杂、最常态的工作也就是要经常对学生进行差错、纠错，但有些错误是在学生做题中错误的频率较高，我们称这样的题为“易错题”，这些题就需要教师将其进行总结、整理，最后集中在课堂上进行策略性讲解。

一、对概念理解不深刻的知识性错误

案例一：填空题：①零是非负数②零是整数③零是自然数④零是偶数⑤零既不是奇数也不是偶数。其中正确的有

（填写正确的序号）

【考点】有理数的概念

【答案】①②③④

【分析】此题考查的是偶数、非负数、整数、自然数、奇数的概念及性质，对于初中的学生而言，五项中最容易出错的就是④和⑤的选择，很多学生会选择⑤是正确的，这就是由于小学对概念理解的不够透彻，单凭死记硬背的知识和概念很容易忘记，那么教师应该怎样采取措施，解决这类问题呢？

【解决措施】教师给学生们讲解这些概念的由来，讲数学的历史：2002年国际数学协会规定0为偶数;2004年中国也规定了0为偶数。那什么又是偶数呢？我们知道偶数的定义是：能被2整除的数就是偶数，因为0÷2=0，没有余数，所以0是偶数。

通过此案例，我们发现，若要让学生对概念有深刻的印象，就必须对概念有深刻的理解，对概念的形成过程，需要教师的深层挖掘，要让学生知其然并知其所以然。概念是学生用来判断归属性问题的依据，比如，有的学生问：“老师，重合算是平行的一种情况吗？”这就是对概念理解的不透，我们不应该直接回答学生是或不是，而是应该反问：“那你先说说两条平行的直线有没有交点？”学生会回答：“没有交点。”老师再问：“那重合的两条直线有没有交点？”学生会说：“有交点，有无数个交点！”这时老师再问：“那你认为重合的两条直线算是平行吗？”生答“不算。”

大家有没有发现，当我们不是直接把答案告诉学生，而是从概念的本身去引导学生思考时，学生自然就理解了，而且从本质上学会了判断和分析问题了。

案例二：计算

学生的解法：原式=3（x+1）+2（x-1）

=3x+3+2x-2

=5x+1

显然，这是把分式计算与解分式方程记混了，那么我们应该如何引导学生呢？有一名老师是这样做的：

她在黑板上呈现两个式子：，

然后请同学们观察并思考这两个式子有什么区别，他们都叫什么？

这样做能让学生在类比中发现问题和矛盾，在思考中重新理解概念，然后，让学生在分别解一下这两道题，夯实对分式计算与分式方程的理解，强化了认知。

以上是对学生再概念理解上犯的 错误采取的措施，这种措施对与 几何图形的性质和判定同样有效，只要老师多学习、勤思考、深研究，总会创造出更有效的方法帮助学生解决易错的问题。

二、思考问题不全面，思维不严谨的错 误

案例三：直线y=kx+b（k≠0）经过点（0，4），它与两个坐标轴围成的三角形面积为4，求这条直线的函数解析式。

此题产生错误的原因是学生在考虑一次函数图像位置时的情况，已知经过点（0，4），只能判定b=4，k的值无法判断，所以k有大于0和小于0两种情况，而学生经常会忽略一种小于零的情况。

这就要求我们教师在给学生训练一次函数的性质时，对函数中的参数进行逆向发问，比如，正向的问题是：一次函数中k>0，b>0时图像在第几象限？改为逆向发问就是：图像在一、二、三象限时kb（k与b的乘积）的符号是什么？图像在一、二、四象限时kb的符号是什么？一次函数图像与y轴交于（0，5）时，经过那几个象限？……进行这种训练后的学生，在逆向思维和周密的思考习惯上能有很大的突破。

案例四：在平面直角坐标系中，抛物线y=a（x+4）（x-2）与y轴交于点A（0，-4），求：（1）a的值.

（2）若P是该抛物线在第三象限部分上的一个动点，Q是直线y=-x上的动点，当以B、O、P、Q为顶点的四边形是平行四边形时，求点Q的坐标。

此题有OB或OB是对角线的两种情况，最后求得Q的坐标有四个，学生经常会出现丢解的问题。

解决这种错误的根源，可以在学平行四边形的时候就进行训练和渗透，比如：给出两条长度不等的线段，让学生探究能画出几种平行四边形，思考方法是什么？

对于学生来讲，最难解决的就是综合探究题，尤其是函数与几何图形综合在一起的题、动点与相似综合在一起的题，然而，对于一个优秀的数学老师，既要有分解大题的能力，也要有分散难点的能力，还要有大单元教学的能力，对于教材中的课时教学就相当于是碎片化的教学，就像教学生一颗一颗的栽树，到了初三总复习时就是要进行网络化的教学了，也就是要把知识体系化，此时呈现给学生的就是一片森林，而要想让学生认识这片森林，就要在平时栽树的时候给他勾画蓝图，也就是训练思维，为后续学习做好铺垫。

三、审题和计算马虎出现的错误

这种错误属于学生自身习惯的问题，据了解，从小学三年级开始，由于学生识字的数量不够多，语文还好，有拼音标注，但有些数学题，就需要老师给学生读，久而久之，老师读题、分析题就养成了一种教学习惯，而学生呢，也养成了依赖的习惯，久而久之，到了初中，因为学生没有养成读题的习惯，所以造成了读题不认真，审题就不认真了，计算还经常看错数，马虎都是因为没有养成仔细阅读的好习惯造成的。

有些优秀的老师是这样做的：每道题都找一名学生读题，然后再找其他学生指出有没有读错或丢字的地方，这样无论是读题的还是听读的学生，都能养成认真的习惯。而对于计算马虎的学生，首先要让他自己检查一遍，然后再互相检查一遍，学生的心理特点就是给别人检查很认真，但不愿意给自己检查，所以，利用镜子原理，让他给别人检查，检查出问题再负责给同学讲明日，这样就能使学生在不知不觉中纠正了自己的错误，能力也得到了全面的提升。

四、解题策略上的错误

近几年，教育教学理念不断更新：核心素养、深度教学、大单元教学……层出不穷，

但这些理念的本质都是让教师跳出教材的僵化使用、跳出中考题型的束缚，是在提倡教育是为了学生的发展而教，而不是为了应考而教，只有师生跳出套路，才能让学生具有灵活应变的能力，才能拥有答题策略和解题技巧。

案例五：

（2016.南京中考）下列长度的三条线段能组成钝角三角形的是（    ）

A.3，4，4           B.3，4，5          C.3，4，6           D.3，4，7

思考这道题的常规方法是：由勾股数可排除B，由三角形两边之和大于第三边可排除D，那么对于A、C又该怎样进行判断呢？有的同学随便蒙一个答案，有的同学用画图的方法来判定，这都是解题策略上的问题。

其实，此题真正的用意是在考查三角形的三边大小与角的大小关系，我们在很多版本的初中数学教材中，只有勾股定理及其逆定理是用来研究直角三角形由边定角、由角定边的问题，然而在教学中，倘若教师在引导学生探究勾股定理的性质时，进一步探究锐角三角形、钝角三角形的三边关系，既能激发学生的学习兴趣，也会让学生对三角形的边角关系有更深入的了解，这样做才能对三角形知识点的探究趋于完整，经过这种探究的学生，再让他解决此题就能直接看出C是正确答案，因为他知道钝角三角形的两条短边的平方和小于最长边的平方，锐角三角形的两条短边的平方和大于最长边的平方。他就可以通过计算得到C是正确答案，也可以比较发现：3，4，4与3，4，6都有3和4，而6>4，所以选C一定是正确的。

五、屡教不改的错误

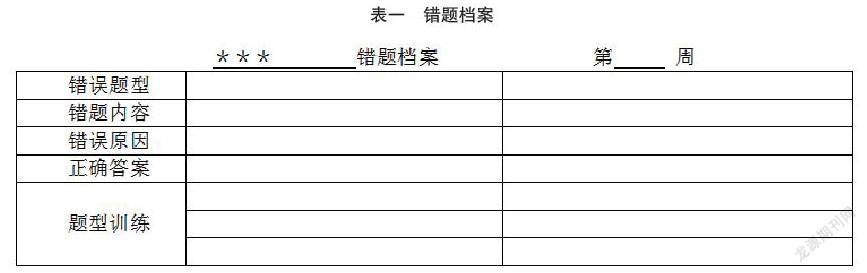
有些学生对某些问题是一错再错，屡教不改，这是因为，大部分学生的学习都只是在进行“浅学习”，他们只注重盲目做题，甚至是被动做题，不重視对数学知识的整体把握和深度理解，所以不利于他们数学思维的形成，由于平时做题都属于章节训练式的碎片化学习，缺少对各个单元的知识点联系起来进行整理和分析，面对这样的学生，有个老师就给出了方案，如表一所示，即：给学生留了一份特殊的周作业：

这个周作业就是教师针对屡错不改的学生发明的，在老师给予讲解和分析后，每周末进行错题整理，并进行自我剖析，里面还设计了让学生针对错题对应找出相应的2-3道同类题型进行纠错训练，这样做既起到了复习巩固的作用，同时也培养了学生自主学习的好习惯，还可以让学生在自我反思中成长，强化了正确的思路，纠正了错误的认知，这种方法，不仅适用于学生的周作业，也适用于学生平时的小测验和各种测试后的总结，还可以用于教师在每次批改作业或测试后建立学生错题库以及习题课的备课等，方法极好。

总之，对学生的错题进行分析、纠正，研究出合理的解决方案，还需要教师不断学习和思考，好的教学，就是要求老师在课堂上以尽可能少的时间达到理想的教学效果，学生用尽可能少的精力，达到较高的学习效率，纠正错题的过程，实际上就是纠正一种习惯或者一种思维的过程，数学教师的责任重大，教师们需要不断的优化教学方法，研究出更好的教学案例，让教学研究成为教育生涯的养料，让教师在学生错误的土壤中浇灌出智慧之花。

参考文献：

[1]潘卫贤.初中数学易错题的成因及其对策[J].数理化学习，2014（4）：15.

[2]张武丰.对初中数学典型易错题的分析[J].考试周刊，2020（011）：97-98.