现代有轨电车线路轨距加宽对独立轮对磨耗的影响

胡耀华，杨新文，钱鼎玮

（1. 同济大学上海市轨道交通结构耐久与系统安全重点实验室，上海 201804;2. 同济大学道路与交通工程教育部重点实验室，上海， 201804）

现代有轨电车大量运用低地板结构，并且独立轮对在低地板车辆结构中被大量采用。 现代有轨电车独立轮对和传统轮对两种不同走行原理转向架同时装配在同一组车上，使得有轨电车在运行过程中加剧了轮缘和钢轨轨距角磨耗现象，轮轨侧磨严重时将影响乘坐舒适性、 列车运行安全性和平稳性。 现代有轨电车由于独立轮对这一特殊结构导致车轮轮缘磨耗较为严重，并且容易造成列车脱轨和晃车等问题，所以找到其解决问题的办法有着很重要的意义[1]。

在轮轨磨耗问题上，国内外大量学者开展了一系列研究，Pearce 和Sherratt[2]是最早对车轮和钢轨磨耗进行理论研究的学者， 考虑当时计算能力有限，他们在得出接触斑轮轨切向蠕滑力和法向接触力后， 利用磨耗指数评价了相应的轮轨磨耗程度。Kalker[3]采用简化理论Fastsim 算法进行轮轨接触应力计算，后来结合材料磨耗模型分析了车轮磨耗情况，得到的结果与实测较为相近。 Zhou 等[4]利用临界平面法以及通过多体动力学软件建立钢轨磨耗与裂纹共存模型，分析了重载铁路钢轨磨耗与裂纹两者互存的制约关系。 Wang 和Gao[5]利用UM 动力学软件和Specht 磨耗模型， 建立了重载铁路钢轨型面磨耗演变的分析模型， 进行了相关计算。Zobory[6]等基于车轮磨耗试验数据，并在现场对统计数据进行分析，建立轮轨型面磨耗模型，将其应用于车轮和钢轨的磨耗预测。Jendel[7]在Archard 磨耗模型基础上，结合试验得到的数据建立轮轨磨耗模型。黄照伟[8]根据实际情况下列车运营条件建立了理论仿真模型，分析了车轮不同形式的侧磨对车辆动力学性能的影响，讨论了车轮的镟修策略。 李霞等[9-10]在建立的车轮磨耗计算模型中，采用改进的三维非Hertz 滚动接触模型， 考虑了车轮每通过接触斑内划分的网格时轮轨接触状态发生改变的情况下，可以更精确地分析车轮滚动时接触斑内的情况。张俊[11]选择Hausdorff 距离匹配算法对现有的槽型轨进行型面匹配， 分析了现有槽型轨型面磨耗的形成原因。杨新文等[12]考虑了独立旋转车轮，建立现代有轨电车车辆-轨道耦合动力学模型，结合Archard 磨耗模型研究了轨底坡对钢轨磨耗的影响。 杨阳等[13]基于Specht 磨耗模型和轮轨多点接触理论，建立了现代有轨电车59R2 槽型轨磨耗模型， 分析了不同曲线段槽型轨的磨耗情况。 丁军君等[14]基于轮轨多点非椭圆接触理论及Archard 材料磨耗模型对低地板有轨电车车轮磨耗的演变过程进行了仿真和模拟研究，对不同轮背内侧距下的车轮磨耗进行了详细分析。 都敏[15]基于弹塑性问题的有限元法对有轨电车轮轨匹配关系进行了不同角度的分析和研究。

列车在小半径曲线轨道（≤350 m）上运行时，轨距要进行合理的加宽设计，这对改善轮轨接触状态、减少和降低轮轨横向力以及减轻车轮磨耗的作用比较显著。 目前我国在小半径曲线情况下有轨电车车辆在槽型轨上运行时的轨距加宽设置暂无统一规范，均参考《地铁设计规范》 GB 50157-2013，如表1 所示。

为了探究现代有轨电车车辆小曲线半径通过时轨距加宽对车轮磨耗的影响，建立了车轮磨耗预测模型， 包括独立轮对的现代有轨电车车辆-轨道耦合动力学计算模型、考虑轮轨多点接触的分析模型及Archard 材料磨耗模型3 个子模型。 基于该磨耗预测模型研究并分析了轨距加宽对低地板有轨电车车辆经过小半径曲线时车轮不同位置磨耗的影响规律。

1 车轮磨耗预测模型

1.1 计算分析思路

现代有轨电车车轮型面预测模型的计算流程如图1 所示。

1） 利用建立的车辆-轨道耦合动力学模型求解轮轨接触点所需要的横移量、摇头角、蠕滑率等动力学参数；

2） 通过Hertz 非线性接触理论求解法向接触力；

3） 利用Kalker 简化理论Fastsim 数值方法求解切向接触力；

4） 通过Archard 材料磨耗模型分析和计算不同轮对不同位置对应的磨耗量。 将车轮最大磨耗深度0.1 mm 作为更新条件并更新车轮型面， 再进入下一步迭代。 图1 为车轮磨耗预测流程。

1.2 有轨电车车辆车辆-轨道耦合动力学计算模型

采用多体动力学软件对70%低地板的有轨电车车辆与轨道系统进行建模，其中车辆模型由“动+拖+动” 形式的3 个模块组成， 动车采用非独立轮对，轮轴包括第1 轮对和第2 轮对，拖车采用独立轮对，轮轴包括第3 轮对和第4 轮对。 模型基本参数如表2 所示。

表2 车辆模型基本参数Tab.2 Basic parameters of the vehicle model

主要考虑有轨电车车辆低速通过曲线时独立轮对的磨耗问题，当车速较低时轮轨激扰主要集中在低频；因此将钢轨视为刚体。

2 结果分析

2.1 模型验证

文献[14]基于Archard 磨耗模型对磨耗演变过程进行模拟，研究了低地板有轨电车车轮磨耗情况。其曲线工况中线路参数设置为：曲线半径100 m，通过速度为平衡速度27 km/h，曲线超高90 mm，轨道不平顺选用德国低干扰谱。 本文采用以上线路参数进行验证， 将车轮的磨耗深度达到0.1 mm 作为踏面更新条件，经过30 次迭代，所得独立旋转车轮磨耗计算结果对比如图2 所示。

图2 轮对内外侧车轮磨耗量对比Fig.2 Comparison of abrasion of inner and outer wheels

由图2 可以看出，本文计算结果与文献[14]计算结果处于同一数量级，外轮踏面位置在计算时出现少量磨耗，对比后发现，是由于列车经过曲线前设置一定的前直线所致，数据体现的轮轨磨耗位置及变化规律总体相似，不同位置车轮磨耗量数值相差较小，可认为本文所建立的车轮磨耗预测模型是可靠的。

2.2 70%低地板有轨电车车辆轮对磨耗特征分析

由于列车车轮镟修工作一般要求车轮运行上万公里，故仿真选择10 000 km 作为线路运行终止条件。

选取独立轮对转向架和非独立轮对转向架的内外侧车轮磨耗进行分析，图3～图6 为有轨电车车轮在轨距加宽为15 mm 时，列车通过不同里程后的磨耗量，其中横轴X 表示车轮踏面横坐标。

将轨距加宽为15 mm 时，独立轮对和非独立轮对不同主要位置列车运营10 000 km 产生的磨耗量统计如表3 所示。

由图3～图6 可知，当轨距加宽为15 mm 时，在列车运营10 000 km 后，不同轮对的不同位置存在不同的磨耗，3 节编组的有轨电车车辆磨耗发生较为严重的部分是第1 轮对和第3 轮对内外侧，对于外侧车轮， 发生磨耗的主要位置在轮缘X=30 mm部分，这是由于当列车进入缓和曲线和圆曲线部分时， 车轮轮缘与外轨轨距角贴靠从而引起较大侧磨；对于内侧车轮，车轮踏面X=0 和轮背X=50 mm分别与钢轨轨顶和护轨发生接触从而使得两部分磨耗较大，此时轮缘与轨距角几乎无接触，内轮侧磨几乎为0。从表3 还可得知，第1 轮对和第3 轮对磨耗中，独立轮大于非独立轮，尤其表现在侧磨，差值最大为0.94 mm，其它轮对侧磨较低，踏面磨耗二者接近，同时，第2 轮对和第4 轮对非独立轮和独立轮的磨耗量较第1 轮对和第3 轮对小很多，但发生磨耗的位置和规律相同。

图3 第1 轮对和第3 轮对外侧车轮Fig.3 First and third wheelsets outside wheels

图4 第1 轮对和第3 轮对内侧车轮Fig.4 First and third wheelsets inner wheels

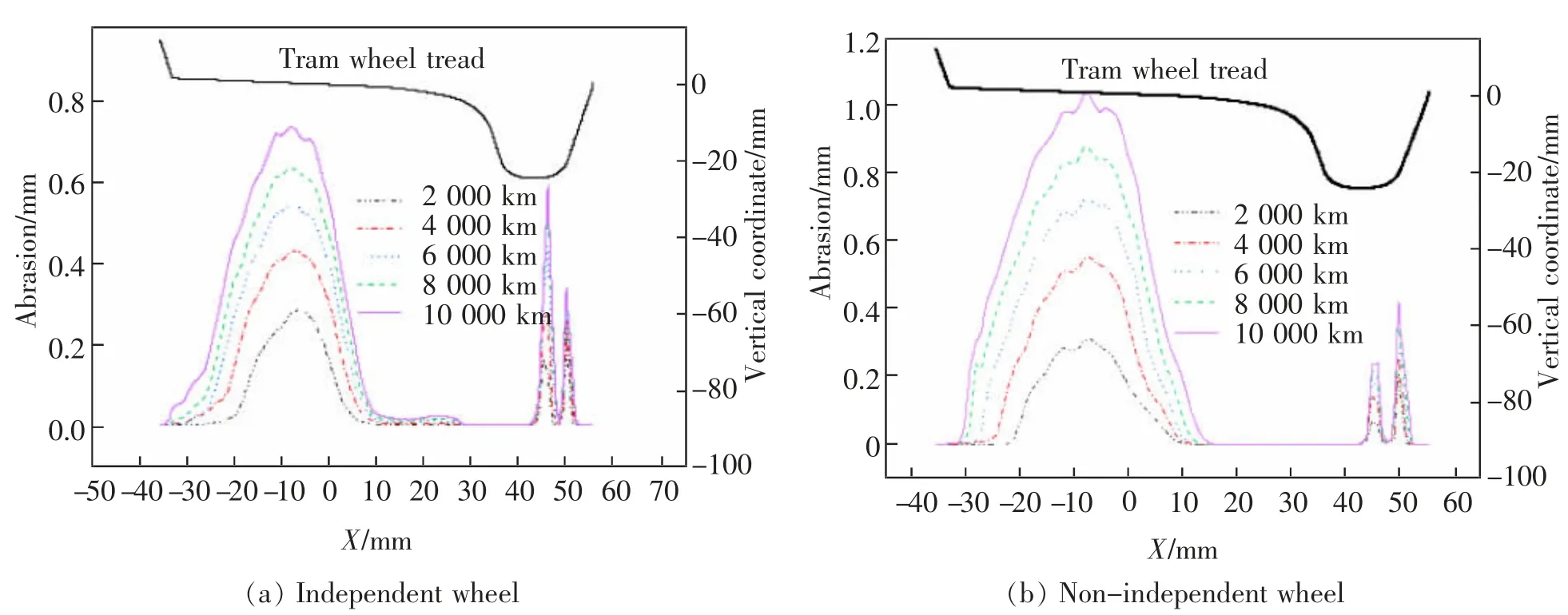
图5 第2 轮对和第4 轮对外侧车轮Fig.5 Second and fourth wheelsets outside wheels

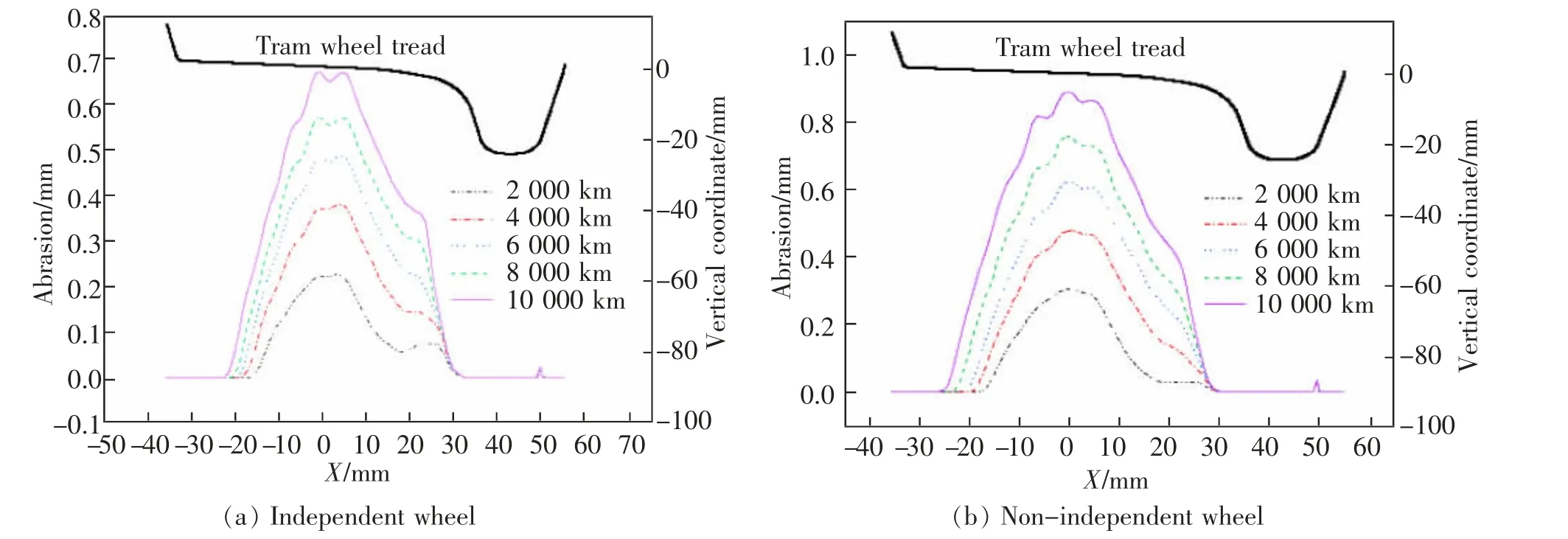
图6 第2轮对和第4轮对内侧车轮Fig.6 Second and fourth wheelsets inner wheels

表3 轨距加宽15 mm 工况下列车通过10 000 km 后各车轮对置磨耗量最大值统计Tab.3 The maximum friction of each wheel after the train passes 10 000 km under the condition of 15 mm widened gauge

另外，表3 从非独立轮对和独立轮对的对比中以第1 轮对和第3 轮对为例，外侧非独立轮对踏面磨耗量1.56 mm，轮缘磨耗量1.94 mm，而独立轮对踏面磨耗量1.75 mm，轮缘磨耗量2.88 mm，二者数据均大于非独立轮对， 尤其独立轮对侧磨十分严重，这是因为在过小半径曲线时，独立车轮没有纵向蠕滑力矩，只能依靠重力复原力进行导向，造成独立轮对在曲线上的冲角较大， 轮轨横向作用力大，侧磨量较非独立轮对大很多；轮对内侧车轮踏面和轮背的磨耗量二者相近，故独立轮对的局限性主要反映在外侧车轮的侧磨量较大。

2.3 轨距加宽对车轮磨耗的影响分析

考虑到地铁设计规范中轨距加宽最大不超过15 mm 的原则，设计了轨距加宽分别为0，5，10，15 mm共4 种工况， 列车在半径50 m 的曲线上运行，速度为27 km/h，研究轨距加宽变化对车轮磨耗的影响。

图7～图10 是4 种轨距加宽工况下列车运营通过10 000 km 后车轮型面变化。

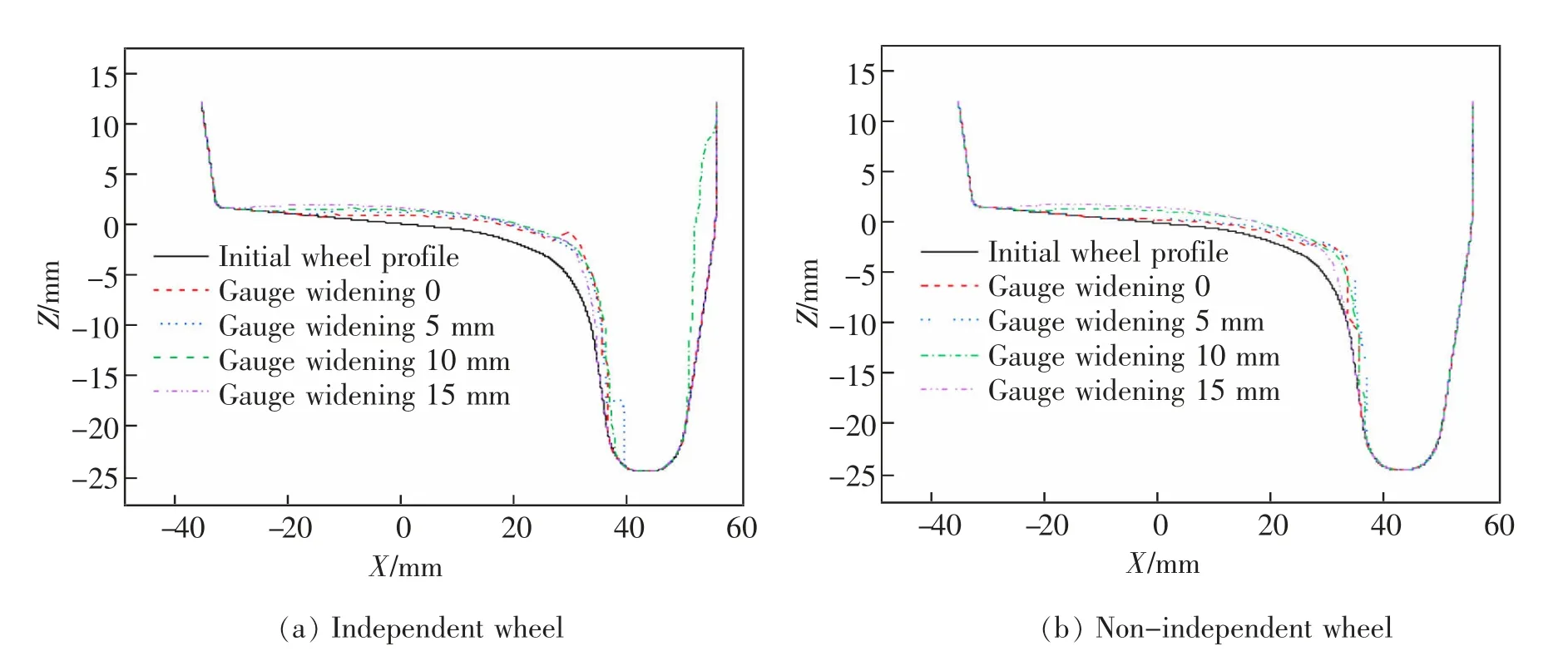
图7 第1 轮对和第3 轮对外侧车轮Fig.7 First and third wheelsets outside wheels

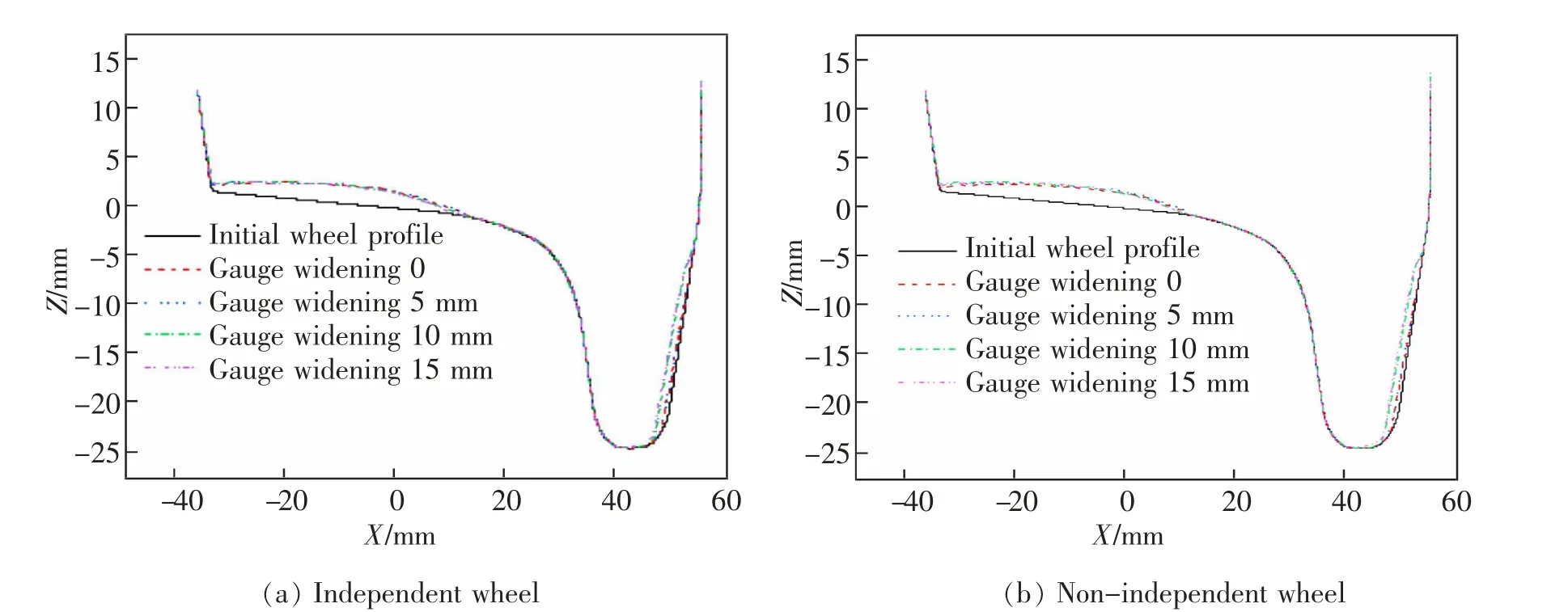
图8 第1 轮对和第3 轮对内侧车轮Fig.8 First and third wheelsets inner wheels

图9 第2 轮对和第4 轮对外侧车轮Fig.9 Second and fourth wheelsets outside wheels

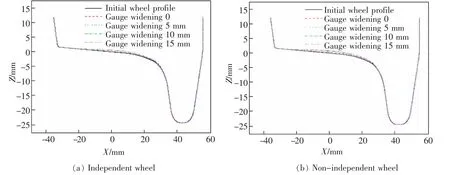
图10 第2 轮对和第4 轮对内侧车轮Fig.10 Second and fourth wheelsets inner wheels

由图7～图10 中各轨距加宽下的车轮型面可知， 第1 轮对和第3 轮对外侧车轮发生磨耗的主要位置为车轮踏面和轮缘，且轨距加宽越小，磨耗越严重， 非独立轮轮缘最大20.24 mm， 独立轮30.55 mm，再次表明独立轮对轮缘位置磨耗更为严重；第1 轮对和第3 轮对内侧车轮发生磨耗的主要位置为车轮踏面和轮背，且独立轮对和非独立轮对磨耗量相近；第2 轮对和第4 轮对外侧车轮磨耗主要为踏面， 但磨耗量远小于第1 轮对和第3 轮对，均在1 mm 以下，有的甚至接近0，轮背处也存在少量磨耗；第2 轮对内侧车轮磨耗主要发生在踏面位置，轮缘处也存在少量磨耗。

另外，从图中可以直观得知，随着轨距的不断加宽，车轮的磨耗宽度不断增加，磨耗产生位置向X 轴负方向移动，在轨距加宽为15 mm 时，同一轮对的磨耗宽度最大，此时磨耗较为均匀，轮轨接触处的磨耗深度降低，磨耗量减小。轨距加宽为15 mm时磨耗量最小，磨耗宽度最大，磨耗最为均匀。

进一步分析， 第1 轮对和第3 轮对外侧车轮侧磨在轨距加宽为0 和5 mm 处十分严重，非独立轮对可达20.24 mm，独立轮对可达30.55 mm，降低使用寿命。随着轨距加宽的增加，侧磨量迅速降低，但独立轮对侧磨仍大于非独立轮对； 其余轮对车轮踏面和轮背位置磨耗量较小， 但会随着轨距加宽的增加而出现少量的上升，当曲线半径小于150 m 的线路，轨距加宽为10～15 mm 时， 各个位置的最大磨耗较为接近，说明当轨距加宽在10～15 mm 时较为理想，另外，从磨耗发生均匀的角度出发，15 mm 加宽为最佳，故轨距加宽应选择磨耗量小，磨好宽度较大的工况。 综上，主要考虑因素为磨耗量的大小，当曲线半径较小的线路，轨距加宽为10～15 mm 总磨耗量较小，其中15 mm 加宽时磨耗宽度最大，磨耗最为均匀。

3 结论

建立了70%低地板有轨电车车辆车轮磨耗预测模型，计算分析了独立轮对和非独立轮对的磨耗特征以及轨距加宽对独立轮对的磨耗规律，主要结论如下。

1） 现代有轨电车车轮磨耗发生较为严重的部分是前导向轮。 对于外侧车轮，发生磨耗的主要位置在轮缘部分；对于内侧车轮，车轮踏面和轮背分别与钢轨轨顶面和护轨发生接触从而使得两部分磨耗较大。

2） 在相同线路条件下，独立轮轮缘磨耗大于非独立轮，差值最大为0.94 mm，两种车轮踏面磨耗较为接近，故独立轮对的局限性主要反映为外侧车轮的侧磨量较大。

3） 列车在曲线半径较小的线路上运行，轨距加宽为10～15 mm 时车轮轮缘磨耗较小， 而轨距加宽为15 mm 时车轮轮缘磨耗较为均匀。