建构数学模型思想 培育学生核心素养

苏文朝

(厦门外国语学校海沧附属学校 福建 厦门 361000)

模型思想，旨在引导学生能够在学习过程中体悟数学和生活的联系，寻找现实生活或具体情境下的问题如何抽象成数学符号(例如数学语言、方程、数量关系、函数等)，进而更清晰的去揭示从特殊到一般，从具象到抽象的描述数量关系及其变化。建立数学模型的过程，其实就是从数学角度观察各类现象，以数学思维去思考问题，说到底，就是数学化思维的培育过程。因此，教师在数学课堂教学活动中，应该精心设计教学环节，有意识的创设针对性训练学生建模思维活动策略，引导孩子挣脱常规课堂的思维模式束缚，逐步渗透模型思想于课堂环节中，从而提升学生的思维品质，达到培育学生核心素养的目标。

1.构建方程模型 强化应用能力

著名教授张奠宙认为“数学应用的本质是数学建模”。他在《小学数学研究》一书中提到：小学数学应用题的求解，可以用算数方法和代数方法，分别建立问题的算数模型与代数模型。[1]如果说模型思想是具有一般性的上位概念，那么，方程思想就是它的最典型的具体体现[2]。建立方程模型，就是对上位概念的一个具体应用。小学数学课堂中，从《用字母表示数》开始，就开启了小学数学从具象思维到抽象思维的序幕。

方程是小学生接触的最抽象的概念，用方程法解决问题是很多学生想避开的“雷区”，相较于方程法解决问题，他们更倾向于用算术法解决。以“相遇问题”为例：甲乙两人分别从相距30千米的AB地方同时相向而行，甲每小时行6千米，乙每小时行4千米，多少小时二者相遇？

学生求解两者的相遇时间，会侧重使用算术法：总路程÷甲乙速度和=相遇时间，但是如果使用方程法，还需要寻找数量关系，解设未知数，列并解方程，相对算术法就繁琐。学生会钟爱算术法也无可厚非，但是，如果题型变换成：甲乙两人分别从AB两地同时相向而行，甲每小时行6千米，乙每小时行4千米，在距离中点2千米处相遇，甲乙相距多少千米？又该如何解答？如果再变题型成：甲乙两人分别从AB两地同时相向而行，甲每小时行6千米，乙每小时行4千米，甲先达到B地后又往回走，在10千米处再次和乙相遇，甲乙相距多少千米？这又该如何解答？

所以，构建方程的模型，最关键就是让学生体会题目中的等价关系，也就是说，学生需要学会从现实情境中，能够寻找并概括其中内涵的等价关系，把这种等价关系转化成数学语言(也就是数量关系)，这种有意识的思维引导和对比提升，大大培养了学生提取题目显性或者隐性条件的能力，进而，在解决实际问题策略过程中，他们的思维方式就会聚焦于数量关系，凝练把数量关系抽象成数学语言的能力，就是用代数式表示数量关系的能力，这是凝练方程模型的过程。如此再辅与丰富例证加以夯实，对于上述的问题，只需要抽象构建两个一般方程模型：S甲+S乙=S总；S甲-S乙=S差，再应用于实际问题的解答过程中，只需要再把方程模型进行分解细化，问题也就迎刃而解。学生的应用意识和解题能力也得以强化提升。

2.另辟面积模型 深耕推理能力

对于面积的学习，学生大多停留在对各个平面图形面积计算公式的记忆，而忽略了这些平面图形面积之间的结构化联系。在复习多边形面积，教师习惯性依照教材设计，依次复习长方形、正方形、平行四边形、三角形、梯形和圆，并以长方形为模型，复习正方形、平行四边形、三角形、梯形和圆面积推导过程，从而建立各个平面图形的结构化关系。笔者在执教过程，在此基础上，另辟梯形为面积模型，以梯形面积公式S=(a+b)h÷2为中心，逐一推导出长方形、正方形、三角形、梯形和圆的面积，从而建立以梯形为联结点的面积结构化网络，重新审视已学的平面图形面积公式，这是对已有知识认知系统的重新组织和建构，加深了对它们的理解和掌握程度，深耕平面图形面积的推理过程，培养了学生的推理能力。

下面论述其推理过程：

梯形面积公式S=(a+b)h÷2，当其中一底(b)逐渐变小为0，则由梯形演变成一个三角形，这时可理解为三角形是一个其中一底(b)为0的梯形，运用梯形面积公式S=(a+b)h÷2=(a+0)h÷2=ah÷2；当梯形的两个底变成一样长，即a=b时，梯形变成一个平行四边形，运用公式S=(a+b)h÷2=(a+a)h÷2=2ah÷2=ah；当梯形的上下底一样长时，且两腰等于高时，梯形变成一个长方形，长即底，宽即高(b=h)，S=(a+b)h÷2=(a+a)h÷2=2ab÷2=ab，同理可推理证明得正方形面积公式。

最难是由梯形面积推导，我们借助图形来推理分析会更清晰，如图1所示。

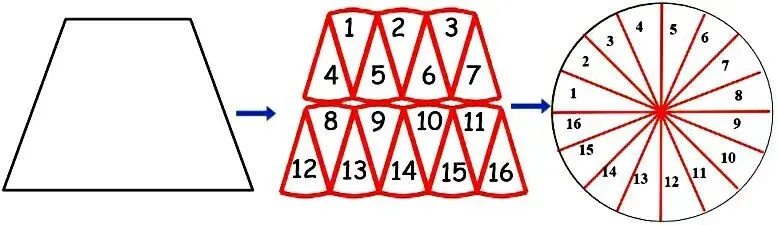
图1

虽然学生已经掌握了从长方形出发去推导其他几个平面图形面积公式的方法，但是，通过我们另辟梯形面积为模型，逆推其他几个平面图形面积公式，如此，学生在图形的变与不变的过程中，感受到几个平面图形之间的深刻联系，在推理面积公式的过程中，学生对于平面图形面积之间的结构化联系也更加深入，结构化思维和推理能力都在这个几何模型的创设和应用中得到了提升。

不仅如此，在后面学习长方体、正方体、圆柱、乃至于三棱柱，四棱柱、五棱柱......学生都能以此为几何模型的推导方式为思维联结点，寻找这几个柱体的共性特征进行体积推理。

3.透析模型价值 享乐趣悟思想

模型思想对于促进学生的数学理解有积极且重要的作用，这体现在它的数学价值和教育价值。[3]而这个数学价值，主要体现在对数学的理解上，学生从机械记忆到理解记忆，从形象思维到抽象思维，整个过程，其实是由简单到复杂，由具象到抽象的转变，这时候，模型思想就能够很好的辅助学生去理解、去感悟、去体验这种转变过程的乐趣。从另外一方面讲，模型思想的培养，其实就是对学生思维能力的培养，这不是简单认为是为了模型思想而训练模型思想，而是在培养模型思想的同时，学生其他方面的核心素养能够在应用模型解决问题的过程中得到提升，这种提升就是模型思想教育价值所在。

弗赖登塔尔指出：‘学习数学就是学习数学化’。所谓数学化，是指从数学的角度看现象、用数学思维想问题，用数学方法解决和解释问题，建立数学模型就是数学化，就是在用模型思想看现象；用模型思想思考问题的本质；应用模型思想去带动思维品质的提升；用模型思想去为学生的终身发展奠基。