基于等效黏性阻尼模型的非比例阻尼体系反应谱CCQC 法

2021-11-12孙攀旭

工程力学 2021年10期

孙攀旭，杨红

(1. 郑州大学土木工程学院，郑州 450001；2. 重庆大学土木工程学院，重庆 400045；3. 重庆大学山地城镇建设与新技术教育部重点实验室，重庆 400045)

振型分解反应谱法建立在模态叠加法基础上，通过将多自由度体系解耦为单自由度体系，结合给定的地震反应谱，可计算对应模态下的地震作用效应，从而依据振型组合方法得到结构的地震作用效应[1-2]。振型分解反应谱法实质上是一种将动力问题简化为静力问题的方法，具有表达形式简单的优点。因此，振型分解反应谱法被广泛用于工程设计中，是各国规范的主要抗震设计分析方法[3-6]。

对于由不同阻尼特性材料组成的非比例阻尼体系，传统的实模态叠加法不再适用[7-9]，导致对应的反应谱CQC(Complete Quadratic Combination)法无法直接用于计算结构的地震作用效应。针对该问题，在基于黏性阻尼模型的复模态叠加法基础上，结合平稳随机理论，部分学者推导了适用于非比例阻尼体系的反应谱CCQC(Complex Complete Quadratic Combination)法表达式[10-15]，但该方法的表达形式复杂，涉及位移相关系数、速度相关系数和位移-速度相关系数的计算，不便于工程应用。Sinha 等[16]忽略非比例阻尼体系中位移与速度的相关性，推导了非比例阻尼线性体系的反应谱SRSS(Square Root of the Sum of the Square)法表达式。俞瑞芳等[17-18]分析了相关系数随频率比的变化规律，发现位移-速度相关系数在频率比较小时不可忽略，其分析结果表明反应谱CCQC 法不可直接简化为反应谱SRSS 法，并进一步提出了考虑部分相关性的反应谱复振型平方组合CPQC(Complex Partial Quadratic Combination)法。综上可见，相比基于黏性阻尼模型的反应谱CQC 法，基于黏性阻尼模型的反应谱CCQC 法增加了位移-速度相关系数、速度相关系数的计算，计算过程更为复杂。由于位移-速度相关系数的影响，振型之间的相关性也更复杂，对于自振频率分布稀疏的非比例阻尼体系，反应谱CCQC 法无法直接简化为忽略相关系数的反应谱SRSS 法。此外，应注意的是黏性阻尼模型的阻尼矩阵构造存在明显困难，阻碍了其推广应用；采用常用的分块Rayleigh 阻尼模型时，阻尼矩阵依赖于振型组合的选择[19-20]，导致基于黏性阻尼模型的反应谱CCQC 法计算结果不唯一、合理性不易被判定。

相比黏性阻尼模型，复阻尼模型具有阻尼矩阵易构造的优点，刘庆林等[21-22]在基于复阻尼模型的复模态叠加法基础上，结合平稳随机理论，推导了基于复阻尼模型的反应谱CCQC 法。但基于复阻尼模型的反应谱CCQC 法计算的谱矩需要引入两个相关系数，对应的振型组合表达式较复杂。此外，更明显的问题是复阻尼模型存在时域发散、非因果性等理论缺陷[23-26]，导致基于复阻尼模型的反应谱CCQC 法的正确性有待进一步验证。

与复阻尼模型等效的黏性阻尼模型不但保留了阻尼矩阵易构造的优点，还克服了复阻尼模型的时域发散、非因果性等缺陷。本文在基于等效黏性阻尼模型的复模态叠加法基础上，结合虚拟激励法和平稳随机理论，推导出反应谱CCQC 法实数表达式，公式表达简单，且计算结果唯一，合理性易被判定，可直接用于计算非比例阻尼体系的地震作用效应。

1 常用的非比例阻尼体系反应谱法

首先对已有的非比例阻尼体系地震作用效应常用计算方法进行介绍，以便于后文的算例分析，并可与本文建立的方法(见第2 节)进行对比。

1.1 基于能量法的反应谱CQC 法

基于黏性阻尼模型的多自由度体系时域运动方程为：

对于由不同阻尼特性材料组成的非比例阻尼体系，阻尼矩阵不再满足经典阻尼条件，传统的实模态叠加法不再适用。为了沿用实模态叠加法，一些学者建议，可借助于能量法将非比例阻尼体系近似等效为比例阻尼体系[27-29]。

采用无阻尼模态分析，式(1)对应的实振型向量为：

上述理论分析表明，基于能量法的反应谱CCQC 法实质上是一种近似解耦的计算方法，不能充分考虑结构的非比例阻尼特性。

1.2 基于分块Rayleigh 阻尼模型的反应谱CCQC 法

对于非比例阻尼体系，其地震效应计算需要建立在复模态叠加法基础上。由于基于黏性阻尼模型的非比例阻尼体系阻尼矩阵构造是十分困难的，部分学者建议，可采用分块Rayleigh 阻尼矩阵[19-20]，即：

以上分析可见，基于分块Rayleigh 阻尼的反应谱CCQC 法考虑了结构的非比例特性，但式(12)表明，其阻尼矩阵的确定不仅依赖于子结构的振型阻尼比，还依赖于结构无阻尼自振频率ωm和ωn的选择，即依赖于振型组合的选择。选择不同振型的自振频率，构造出不同的阻尼矩阵，必将得到不同的计算结果。因此，基于分块Rayleigh阻尼的反应谱CCQC 法计算结果受振型组合的影响，计算结果不具有唯一性。

2 基于等效黏性阻尼模型的CCQC 法

为解决复阻尼模型的缺陷，引入正负频率共轭关系，可得到基于复阻尼模型的滞变阻尼模型[30-31]，作者建立了与滞变阻尼模型等效的黏性阻尼模型[32]，以及基于等效黏性阻尼模型的复模态叠加法。上述研究成果是本文推导基于等效黏性阻尼模型的反应谱CCQC 法实数表达式的理论基础，因此在2.1 节重复给出部分关键公式。

2.1 基于等效黏性阻尼模型的复模态叠加法

基于复阻尼模型的滞变阻尼模型解决了时域发散问题，但仍存在频响函数非因果的缺陷。为克服滞变阻尼模型中频响函数非因果的缺陷，依据频域本构等效的原则，作者[32]构建了一种等效于滞变阻尼模型的黏性阻尼模型，并得到了等效黏性阻尼模型的时域运动方程为[32]：

等效黏性阻尼模型是一种近似等效的阻尼模型，需要限制其适用范围。以两种阻尼模型的动力放大系数的相对误差小于等于10%作为限制条件，可确定等效黏性阻尼模型的适用范围[32]。等效黏性阻尼模型方程的构建实质上引入了一个等效假定，即：

依据等效假定，式(44)可进一步转化为：

2.2 反应谱CCQC 法相关公式的推导

设g(t)为平稳高斯过程，其自功率谱密度为Sg(ϖ) ，振动频率为正频率，为求响应x(t)的功率谱密度，应用虚拟激励法[33]，构造虚拟地面加速度激励如下：

式(86)即为基于等效黏性阻尼模型的非比例阻尼体系反应谱CCQC 法的实数表达式。

对比式(8)和式(88)可知，式(88)与基于能量法的反应谱CQC 法表达式完全相同。理论分析结果表明，当非比例阻尼体系退化为比例阻尼体系，基于等效黏性阻尼模型的反应谱CCQC 法相应退化为基于能量法的反应谱CQC 法。可见，基于等效黏性阻尼模型的反应谱CCQC 法具有统一性，应用范围更为广泛。

2.3 算例分析及验证

关于基于等效黏性阻尼模型的反应谱CCQC法正确性的验证，采用的验证思路是：首先，采用试验方法验证基于等效黏性阻尼模型的时域计算方法正确性，然后，采用基于等效黏性阻尼模型的时域计算方法验证基于等效黏性阻尼模型的反应谱CCQC 法正确性，从而，实现验证本文提出的基于等效黏性阻尼模型的反应谱CCQC 法正确性的目的。关于基于等效黏性阻尼模型的时域计算方法，作者在已发表文献[32]中采用钢板-阻尼胶片组合板的振动台试验验证了其求解方法的正确性。

以时域计算结果为依据验证本文建立的反应谱CCQC 法(见2.2 节)的正确性，验证分析的流程如图1 所示，其思路、做法与参考文献[11]是相同的。该验证方式的核心思想是，将某条特定地震波作用下结构的时域计算结果作为精确解，据此验证振型分解反应谱法(即本文建立的基于等效黏性阻尼模型的反应谱CCQC 法)计算结果的正确性。如图1 所示，首先计算某条地震波作用下结构的时程动力响应，得到对应的响应峰值；然后计算该地震波的反应谱、对结构进行复模态分析，并按前文所述方法进行振型分解反应谱CCQC组合计算，得到结构的响应峰值；最后，将两种方法计算所得的响应峰值进行对比，并评价基于等效黏性阻尼模型的反应谱CCQC 法的误差。下文将分别以El Centro 波、天津波为例进行分析。

图1 振型分解反应谱法的验证分析流程图Fig. 1 The flow chart of verification analysis of mode superposition response spectrum method

以5 层剪切型框架模型A 为例，对应的质量和刚度分布如图2 所示，上部两层结构为钢结构，对应的损耗因子为0.04，下部三层结构为钢筋混凝土结构，对应的损耗因子为0.10。

图2 模型A 示意图Fig. 2 The schematic diagram of Model A

在模型A 的地震作用效应计算过程中，采用的反应谱CCQC 法不是基于《建筑抗震设计规范》(GB 50011-2010)[3]的设计反应谱进行计算，而是以选定地震波的反应谱为依据进行计算，其目的是避免规范反应谱所涉及的大量地震波反应谱的概率统计特性、场地条件等对该验证过程的干扰。因此，模型A 的场地条件是没有限制的(或者说模型A 可以位于各种类型的场地之上)，即模型A 的输入地震波不涉及场地类别的选择问题，换而言之，模型A 的场地类别必然包含El Centro波和/或天津波对应的场地类别。与此同时，模型A 的输入地震波不需要按照《建筑抗震设计规范》(GB 50011-2010)[3]的规定，要求输入地震波的反应谱在主要周期点附近的谱值与规范反应谱接近，因为模型A 是一个抽象的力学模型，仅进行理论意义上的验证分析，并不涉及规范反应谱的相关问题。

首先，对框架模型A 进行复模态分析，得到结构的自振频率和模态损耗因子。然后，采用基于等效黏性阻尼模型的时域计算方法分别计算不同模态损耗因子对应的El Centro 波、天津波作用下的位移反应谱，结果如图3 所示。最后，分别采用基于等效黏性阻尼模型的时域复模态叠加法(以下简称VCT，详见2.1 节)和基于等效黏性阻尼模型的反应谱CCQC 法(以下简称VCCQC，详见2.2 节)计算模型A 在El Centro 波、天津波作用下的结构最大层位移，所得结果见表1。

图3 地震波的位移反应谱Fig. 3 The displacement response spectrums of seismic waves

表1 模型A 的最大层位移Table 1 Maximum storey displacements of Model A

在表1 中，VCT 是地震波作用下结构的时域计算结果，如前所述，可视为精确解。如表1 所示，模型A 的最大层位移相对误差最大为5.28%，从而证明了基于等效黏性阻尼模型的反应谱CCQC法的正确性。

3 不同振型分解反应谱法的对比分析

在验证了基于等效黏性阻尼模型的反应谱CCQC 法正确性基础上，可将其与《建筑抗震设计规范》(GB 50011-2010)[3]的规范设计反应谱相结合，用于计算结构的地震作用效应。

如图4 所示，以多自由度组成的平面框架结构模型为例，模型是由不同阻尼特性材料组成的12 层平面框架，1 层～7 层为钢筋混凝土结构、8 层～12 层为钢结构，底层高度为4.8 m、其余各层层高均为3 m，各跨的跨度均为6 m，钢筋混凝土柱、梁的截面尺寸分别为400 mm×500 mm、250 mm×500 mm，钢柱、钢梁的截面尺寸分别为HM400 mm×300 mm× 8 mm×10 mm、HM300 mm×150 mm×6 mm×8 mm，各楼层集中质量皆为20 000 kg。抗震设计参数如下：抗震设防烈度为7 度，设计基本地震加速度为0.15g，设计地震分组为第二组，场地类别为Π 类。与模型B 相比，模型C 仅1 层～4 层增设了X 型金属耗能阻尼器，模型D 则在1 层～12 层均增设了X 型金属耗能阻尼器，材料参数见表2。

表2 不同材料的参数Table 2 Parameters of different materials

图4 平面框架模型的示意图Fig. 4 Schematic diagrams of the plane frame models

依据损耗因子与阻尼比的近似2 倍换算关系[34-36]，VCCQC 可直接利用规范反应谱计算结构的地震作用效应。依据规范反应谱，结合结构的模态参数和场地条件，对结构施加计算所得的等效水平力，分别采用VCCQC、基于分块Rayleigh 阻尼模型的反应谱CCQC 法(RCCQC)和基于能量法的反应谱CQC 法(EVCQC)计算模型B、C 和D 的地震作用效应。

对于模型B，结构的一阶振型和二阶振型的模态有效质量参与系数较大(见表3)，一阶振型为整体一阶横弯振型，二阶振型为整体二阶横弯振型。因此，模型B 中贡献较大的振型为一阶振型和二阶振型；对于模型C，结构的一阶振型和六阶振型的模态有效质量参与系数较大(见表3)，一阶振型为上部一阶横弯振型，六阶振型为上部四阶横弯、下部一阶横弯振型，因此，模型C 中贡献较大的振型为一阶振型和六阶振型；对于模型D，结构的一阶振型和二阶振型的模态有效质量参与系数较大(见表3)，一阶振型为整体一阶横弯振型，二阶振型为整体二阶横弯振型，因此，模型D 中贡献较大的振型为一阶振型和二阶振型。

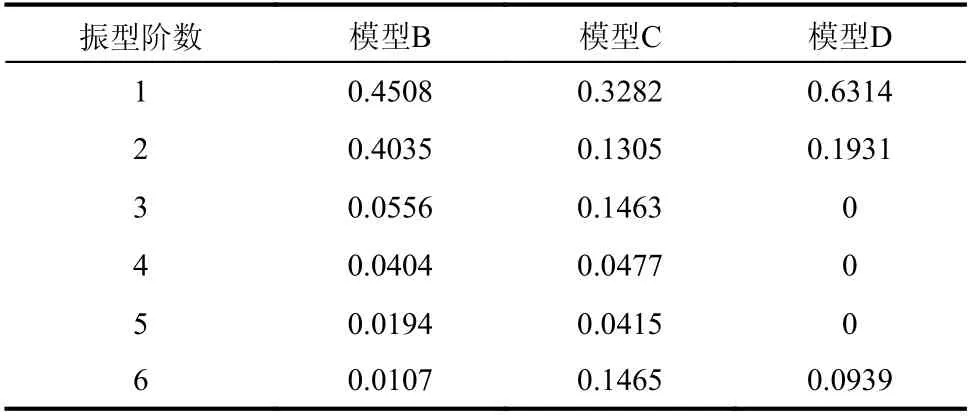
表3 不同模型的模态有效质量参与系数Table 3 Modal effective mass participation coefficients of different models

对于2 自由度以上的多自由度体系，RCCQC需要选择某两阶振型才可以完成相关计算，依据模态分析结果，本文仅以基于一阶振型和二阶振型的反应谱CCQC 法(RSCCQC)、基于一阶振型和六阶振型的反应谱CCQC 法(RXCCQC)为例，对模型B、C 和D 进行对比分析。

采用文献[37]建议的方法计算不同模型的非比例阻尼特征指数，EVCQC 采用的是等效比例阻尼模型，对应的非比例阻尼特征指数为0，VCCQC、RSCCQC 和RXCCQC 的非比例阻尼特征指数如表4 所示。由表4 可知，模型B、模型C 和模型D 的非比例阻尼特性依次逐渐增强。

表4 不同模型的非比例阻尼特征指数Table 4 Index of non-proportionality of plane frame

本文皆以柱的地震剪力为指标，分析不同方法的差异。

对于模型B，不同方法计算得到的柱剪力如图5 所示，图中“柱编号”代表不同楼层的中柱，其对应的平面位置如图4 所示。由图5 的计算结果可知，VCCQC、RSCCQC、RXCCQC 和EVCQC 计算得到的柱剪力最大相对误差小于10%，结果近似相等。分析结果表明，对于非比例阻尼特性较弱的混合结构，EVCQC 的计算结果即可满足要求。同时，对于非比例阻尼特性弱的混合结构，振型组合的影响较小，采用不同振型组合的分块Rayleigh 阻尼模型反应谱CCQC 法计算结果近似相等。

图5 不同反应谱法计算的模型B 柱剪力对比Fig. 5 Comparison of column shear forces of Model B calculated by different response spectrum methods

对于模型C，不同方法计算的柱剪力如图6所示，对比分析可知：

图6 不同反应谱法计算的模型C 柱剪力对比Fig. 6 Comparison of column shear forces of Model C calculated by different response spectrum methods

1) RSCCQC 和VCCQC 计算得到的柱剪力最大相对误差大于10%，RXCCQC 和VCCQC 计算得到的柱剪力最大相对误差小于10%，表明RSCCQC和VCCQC 的计算结果差异较大，RXCCQC 和VCCQC 的计算结果近似相等。由模态分析可知，模型F 的上部结构主要受一阶振型的影响，下部结构主要受六阶振型的影响。因此，采用RXCCQC可得到合理的计算结果，进而间接证明了VCCQC的正确性。对于非比例阻尼特性较大的混合结构，可采用基于分块Rayleigh 阻尼模型的反应谱CCQC 法和基于等效黏性阻尼模型的反应谱CCQC法计算结构的地震作用效应。

2) RSCCQC 和RXCCQC 的计算结果差异较大，表明振型组合对基于分块Rayleigh 阻尼模型的反应谱CCQC 法的影响较大，采用不同振型组合得到的计算结果差异无法忽略，选择不合理的振型组合将导致计算结果偏差较大。在实际工程计算中，合理振型的选择并不总是容易的，且对于复杂结构不能仅考虑某两阶振型的影响，这些因素都将导致其计算结果的合理性不易被判定。

3) EVCQC 和VCCQC 计算得到的柱剪力最大相对误差小于10%，计算结果近似相等。与模型B 的规律相似，EVCQC 的计算结果唯一，可用于计算非比例阻尼特性弱的混合结构的地震作用效应。

对于模型D，不同方法计算的柱剪力如图7所示，对比分析可知：

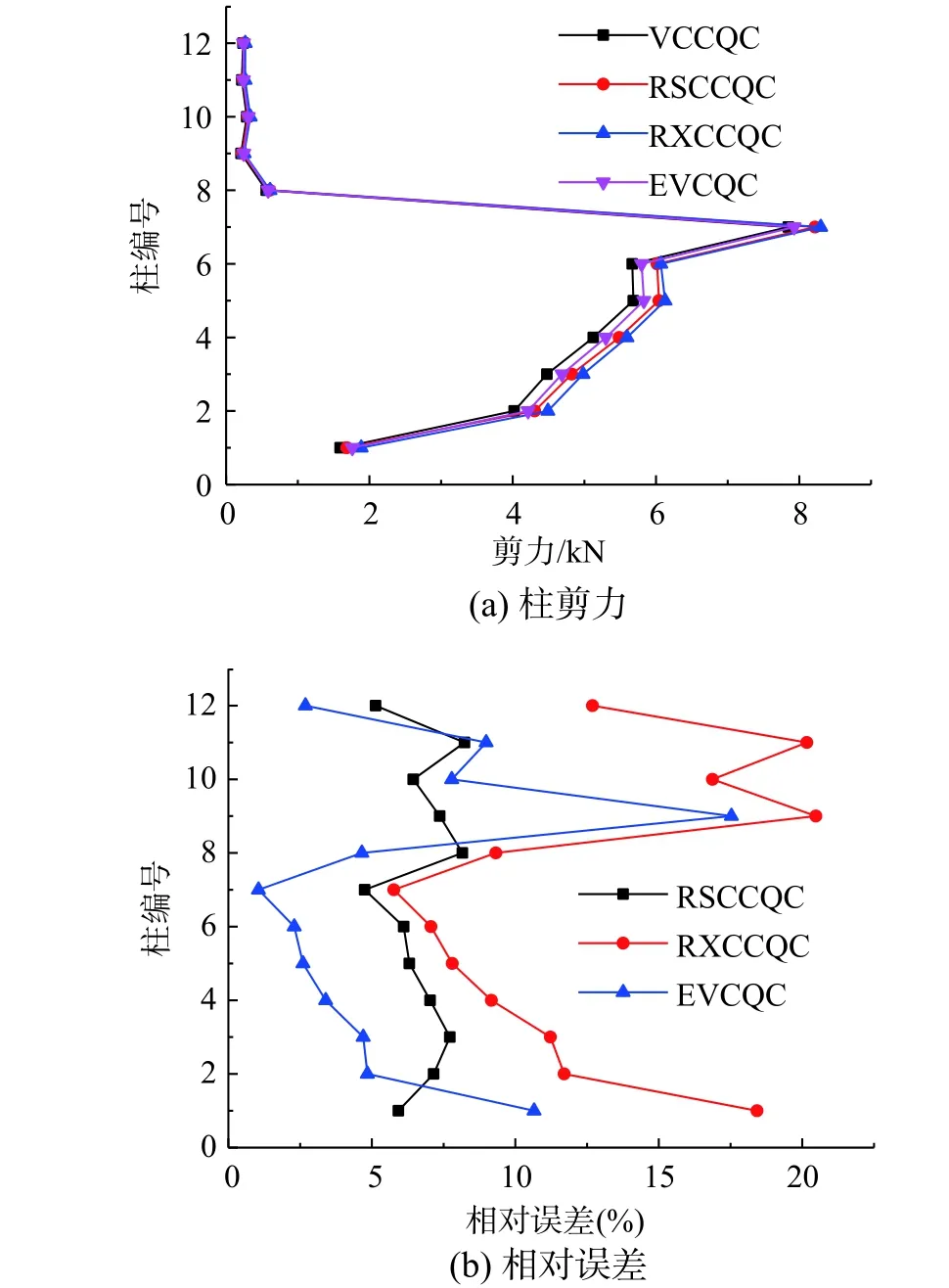
图7 不同反应谱法计算的模型D 柱剪力对比Fig. 7 Comparison of column shear forces of Model D calculated by different response spectrum methods

1) RSCCQC 和VCCQC 计算得到的柱剪力最大相对误差小于10%，RXCCQC 和VCCQC 计算得到的柱剪力最大相对误差大于10%，表明RSCCQC和VCCQC 的计算结果近似相等，RXCCQC 和VCCQC 的计算结果差异较大。由模态分析可知，随着阻尼器布置从1 层～3 层转变为1 层～12 层，结构的重要振型由一阶振型和六阶振型转变为一阶振型和二阶振型。因此，采用RSCCQC 将得到合理的计算结果。与模型C 的规律相似，基于分块Rayleigh 阻尼模型的反应谱CCQC 法计算结果的可靠性依赖于振型组合的选择。

2) EVCQC 和VCCQC 计算得到的柱剪力最大相对误差大于10%，计算结果差异较大。可见，EVCQC 作为一种近似解耦的计算方法，不能充分考虑结构的非比例阻尼特性，随着结构非比例阻尼特性的进一步增强，计算结果将会出现较大偏差。