沪苏通大桥风-车-桥耦合系统非线性动力响应研究
2021-11-12郭薇薇
徐 曼,曾 滨,乔 宏,许 庆,郭薇薇,夏 禾
(1. 中冶建筑研究总院有限公司研究院,北京 100088;2. 北京建筑大学土木与交通工程学院,北京 100044;3. 北京交通大学土木建筑工程学院,北京 100044)
公铁两用斜拉桥能合理利用空间、节省建设费用[1]。随着我国高速铁路的快速发展,越来越多的大跨度高铁桥梁选用斜拉桥的设计方案。大跨度斜拉桥通常建设于跨江、海、峡谷等地形区域,风场环境复杂。并且,随着跨径的增大,桥梁刚度逐渐降低,对风和列车荷载的敏感性逐渐增加,在拉索垂度效应、结构大变形等几何非线性因素影响下,动力荷载下的桥梁响应通常呈现出中小跨度桥梁所没有的非线性特性[2]。国内外学者对风-车-桥耦合振动问题进行了大量研究[3-13],关注了横风作用下车-桥系统响应[3,5],大跨度桥梁气动特性[3-7],考虑几何非线性因素的桥梁非线性响应及结构安全分析[12-14]等。
由于大跨度斜拉桥结构形式的独特性和风场环境的复杂性,每一座大跨度桥梁的安全运行均需遵循严谨细致的研究分析。为了保证桥梁结构自身的服役性能及桥上运行列车的安全性与平稳性,研究复杂风场环境和高速列车荷载下的大跨度斜拉桥非线性响应十分必要。
沪苏通公铁两用长江大桥(以下简称沪苏通大桥)是世界首座跨度突破1 km 的公铁两用型斜拉桥,该桥地处长江中下游,受海洋性季风影响,风场条件复杂,车辆运行时直接暴露于自然风场,风对桥梁及行驶车辆的作用显著。刘德军等[15]和张骞等[16]以沪通长江大桥为研究背景,进行了不同风速激励下列车以不同速度通过桥梁时系统的动力响应分析。然而,上述分析中未考虑桥址区实际风场作用特点,且忽略风荷载非线性对车-桥耦合系统响应的影响。
因此,本文以沪苏通大桥为工程背景,基于实测风场数据,考虑几何非线性因素影响,进行沪苏通大桥的风-车-桥耦合振动分析,对保证大桥在自然风场中的结构安全以及行车安全性、舒适性,具有重要的研究价值和工程意义。
1 工程概况
沪苏通大桥全长2296 m,主跨跨径1092 m,为双塔三索面斜拉桥,具体桥跨布置如图1 所示。上层桥面为6 车道高速公路;下层为4 线铁路,分别为2 线通苏嘉城际铁路(设计速度250 km/h)和2 线沪通铁路(设计速度200 km/h)。

图1 沪苏通大桥立面布置图 /mFig. 1 Elevation of Hu-Su-Tong Yangtze River Bridge
大桥采用钢桁架主梁,横断面如图2 所示。主梁钢桁架弦杆采用带肋空心矩形截面,由500 MPa级高强钢板制造,共164 个节间;主塔及桥墩采用C60 混凝土;斜拉索钢绞线采用2000 MPa 级高强度平行钢丝。
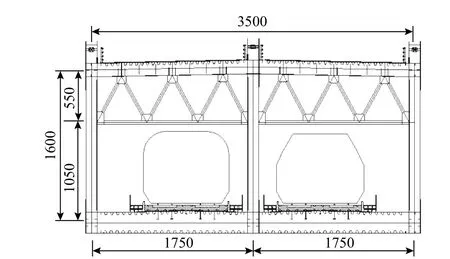
图2 沪苏通大桥主梁横断面 /mmFig. 2 Cross section of girder of Hu-Su-Tong Yangtze River Bridge
2 风-车-桥耦合系统建立
2.1 风荷载模型
沪苏通大桥地处长江中下游,临近入海口,受海洋季风气候影响大,风场环境复杂,规范给出的设计风速无法准确描述桥位处的风场特征。笔者开展了实地风场测试[17],提取风场特征,经比较,规范风谱与实测风谱数据差异明显,采用实测谱参数模拟的风速时程与实际风场特征吻合度高。
基于沪苏通大桥节段模型风洞试验[18]获得的三分力系数,结合基于实测的功率谱参数模拟主梁横/竖桥向、主塔横桥向等多组一维脉动风速场,以14 m 为主梁模拟点间隔,考虑上、下桥延伸距离,建立全桥风荷载模型。在此基础上,对车辆运行位置处线性插值计算得到车辆风荷载。表1 给出了瞬时风速30 m/s 时主梁跨中抖振风荷载极值。

表1 瞬时风速30 m/s 时沪苏通大桥主梁跨中抖振风极值Table 1 Max buffeting wind load at mid-span with U=30 m/s
2.2 桥梁模型
本文采用ANSYS 建立沪苏通大桥全桥有限元模型,采用Ernst 公式[18]修正拉索弹性模量以表征垂度效应。
提取主梁的前5 阶振型及自振频率如表2 所示,将其与文献[18]给出的沪苏通大桥有限元模型的自振特性比较。可以看出,除纵飘振型外,本文桥梁模型的前5 阶振型与文献一致,且自振频率的差异率在±5%以内,纵飘是大跨度桥梁的常见低频振型,符合客观规律,可认为本文模型有效。
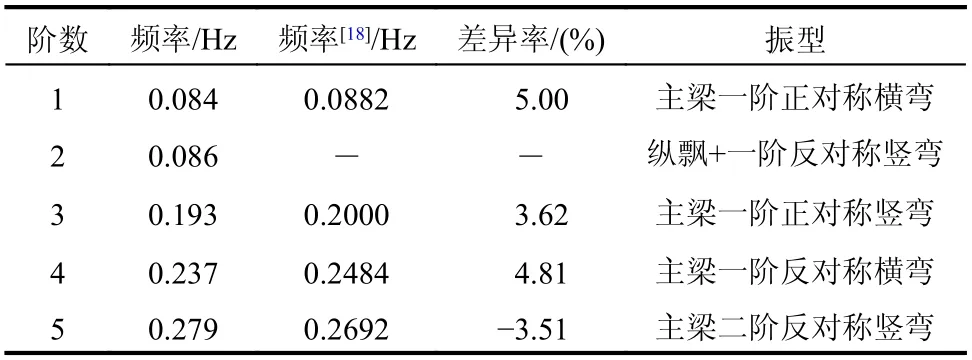
表2 沪苏通大桥自振频率及振型特点Table 2 Natural frequencies and mode-shape characteristics
2.3 非线性因素
由于风-车-桥耦合分析中,桥梁结构一般仍处于弹性状态,因此本文仅考虑几何非线性因素的影响。考虑梁柱效应与大位移效应的影响,建立桥梁结构的非线性运动方程:

式中:M、C和K分别为质量矩阵、阻尼矩阵和刚度矩阵;下标b 代表桥梁;刚度矩阵Kb与桥梁的位移向量Xb相关,并由结构自身的弹性刚度矩阵KE和随位移变化而改变的几何刚度矩阵KG组成:

由式(2)可知,为了考虑几何非线性的影响,需在每一计算时间步之后重新计算桥梁的内力和位移,以更新刚度矩阵进行下一时间步的计算。
自然风场中,桥梁各位置响应各异,结构变形导致风攻角变化而影响风荷载分布,进而改变桥梁位移响应,体现出风荷载的空间非线性特征[19]。
2.4 风-车-桥耦合模型
以16 节车辆编组((3 动+1 拖)×4)的CRH2 高速列车为研究对象,基于刚体动力学假定建立车辆模型。车辆模型与桥梁模型之间的相互作用通过轮轨关系实现,计算时假定横向蠕滑、垂向密贴。将风以外荷载的形式作用于车-桥耦合系统,轨道不平顺则采用德国低干扰谱模拟获得。最终建立风-车-桥耦合系统的运动方程为:

式中:下标v 为车辆;Fvb和Fbv分别为车辆与桥梁系统间的相互作用力;上标st、bf 分别为静风荷载和抖振风荷载。
采用全过程迭代法[20]对耦合系统的动力响应进行求解,求解过程中考虑桥梁结构非线性的影响。考虑到受荷载作用的最不利情况,在以下分析中,桥梁动力响应取自直接承受列车荷载作用的铁路桥面节点。
3 风-车-桥系统非线性动力响应分析
设定瞬时风速30 m/s,车速200 km/h 为基本工况,多种非线性工况风-车-桥耦合系统动力响应结果如下。
3.1 耦合系统分析模型的验证
为验证耦合动力分析结果的有效性,本节以竖向加速度响应为例,绘制了主梁多位置处的竖向加速度时程曲线和低频区频谱曲线如图3 所示。

图3 主梁竖向加速度时程及频谱曲线Fig. 3 Bridge vertical acceleration and spectrums
根据图3(a),竖向加速度呈现出明显的受激振动特征,列车行驶过程,主梁自左向右呈现出典型的此起彼伏振动趋势,符合客观规律。根据图3(b),可识别0.2 Hz 和0.4 Hz 的自振频率,分别与主梁一阶正对称竖弯(0.193 Hz)和主梁二阶正对称竖弯(0.400 Hz)吻合,认为耦合系统分析结果与桥梁模型的特征吻合。
3.2 非线性因素对桥梁动力响应的影响
以不考虑非线性因素的工况为基本对照,分析非线性因素对风-车-桥耦合系统桥梁动力响应的影响程度,得到的桥梁动力响应最大值如表3。图4 给出了主梁跨中竖向加速度时程曲线对比,图5 给出了考虑非线性因素下桥梁各动力响应相对差。

表3 不同非线性因素下桥梁动力响应最大值Table 3 Bridge maximum dynamic responses under nonlinear factors

图4 多工况桥梁跨中竖向加速度时程曲线Fig. 4 Vertical acceleration histories of bridge on mid-span in different cases
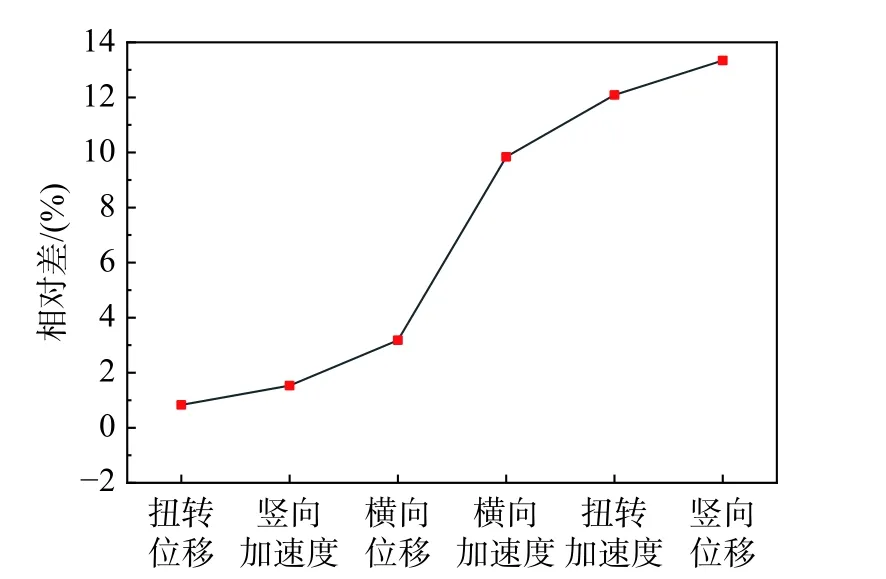
图5 考虑组合非线性因素的桥梁响应相对差Fig. 5 Relative error of bridge responses between linear and nonlinear conditions
由表3 可知,非线性因素对桥梁动力响应影响较大,其中大位移效应影响最大,垂度效应对竖向动力响应的影响较大。梁柱效应的影响较小,且计入活载内力前后,梁柱效应影响差异小。根据图4,除幅值变化外,非线性工况下主梁响应的波动强度更明显。根据图5,综合非线性因素后,竖向位移、扭转加速度、横向位移受影响程度最大,达到10%以上。
3.3 非线性因素对车辆动力响应的影响
图6 给出非线性/线性工况桥上列车动力响应最大值相对差曲线,图7 给出了某节车体在多工况下的横向加速度曲线。

图6 非线性与线性工况的列车响应相对差Fig. 6 Relative error of train responses between linear and nonlinear cases
由图6(a)可知,非线性因素对车辆的多项动力指标有影响,其中,Sperling 竖向受影响最大,达到12.75%,除横向加速度外,其余动力指标影响程度均在5%左右。结合图6(b)和图7,大位移效应导致车辆动力响应峰值增大,且显著增大低频成分,垂度效应对车辆竖向动力指标的影响较为显著,梁柱效应对车辆动力响应的影响很小。
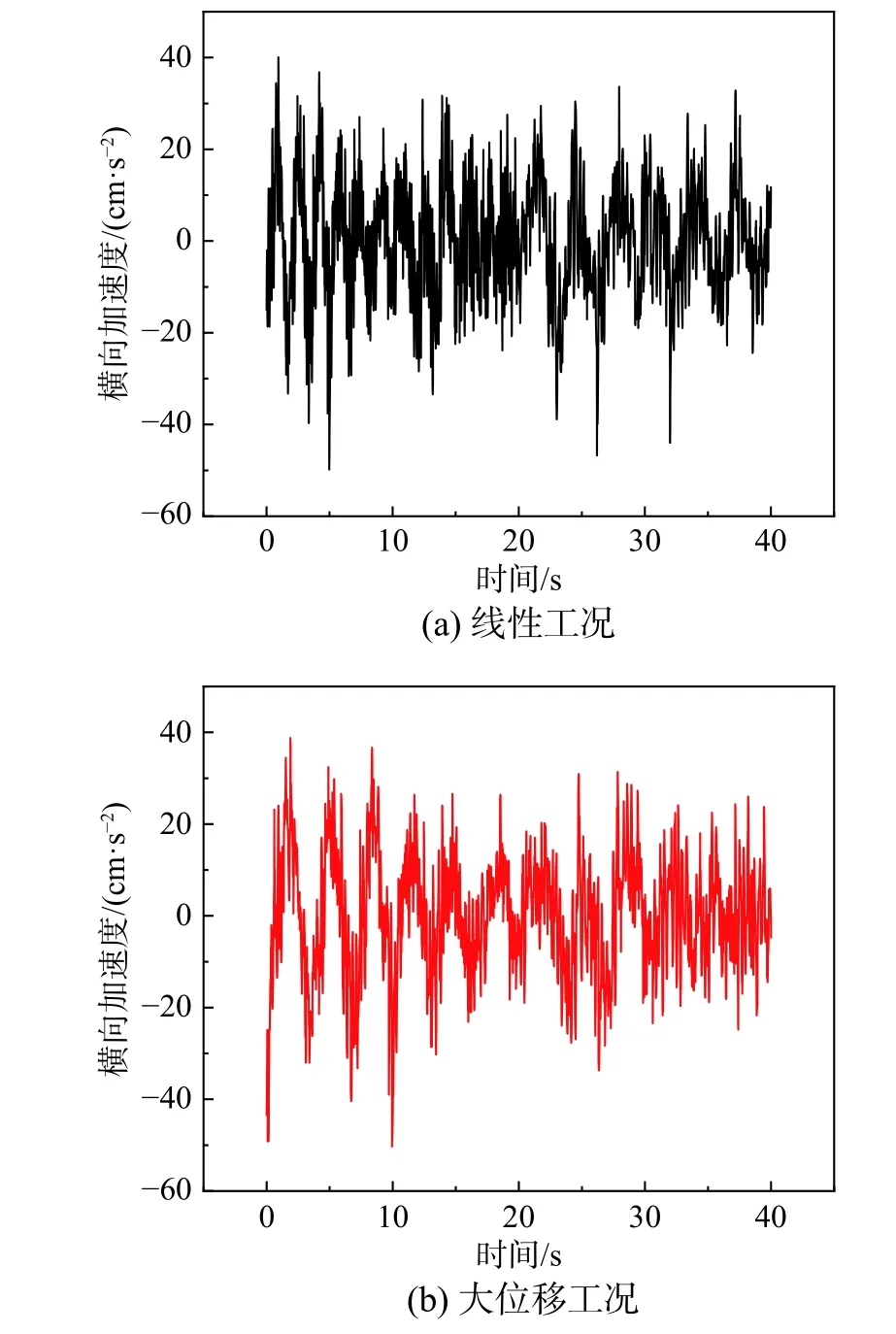
图7 多工况下车体横向加速度时程曲线Fig. 7 Horizontal acceleration histories of train in different cases
3.4 考虑非线性因素的行车安全性分析
基于上述分析,采用考虑非线性因素的风-车-桥耦合模型进行多工况下的车-桥响应分析,得到车速200 km/h,瞬时风速从0 km/h~40 m/s 时的9 组工况下车辆最大动力响应,和瞬时风速30 m/s,车速160 km/h~250 km/h 的5 组工况下车辆最大动力响应如表4 所示。图8 给出了不同车速和不同风速工况下的车辆轮重减载率最大响应曲线。

图8 车辆轮重减载率最大值随风速/车速的变化曲线Fig. 8 Maximum wheel off-load index of train vs. wind/train speeds

表4 不同风速/车速下车辆动力响应最大值Table 4 Maximum dynamic responses of train under various wind/train speeds

续表4
根据《铁道车辆动力学性能评定和试验鉴定规范》[21]和铁道部《铁道机车动力学性能试验鉴定方法及评定标准》[22],轮重减载率应小于0.6(图8 中虚线)。
由表4 及图8 可知,当车速为200 km/h,瞬时风速超过35 m/s,或当瞬时风速为30 m/s,车速超过210 km/h 时,车辆轮重减载率指标超出安全阈值,车辆的安全性能受到威胁。
4 结论
本文以沪苏通大桥为工程背景,考虑大跨度斜拉桥在自然风场中的几何非线性特征,基于实测风场特征模拟风荷载,建立风-车-桥耦合系统动力模型,通过多工况计算,分析了非线性因素对桥梁与车辆动力响应的影响,并给出沪苏通大桥行车安全性分析,主要结论如下:
(1)根据桥梁模型自振特性和动力响应频谱分析,本文的桥梁模型及考虑几何非线性因素的风-车-桥耦合系统动力分析结果,符合客观规律并与既有研究结果吻合。
(2)几何非线性因素对风-车-桥耦合系统振动的影响不可忽略,考虑非线性因素时,桥梁和车辆的多个动力响应指标均有一定程度的增大,忽略非线性因素可能导致结构动力响应分析和行车安全性分析偏不安全。
(3)非线性因素中,大位移效应对桥梁和车辆的动力影响最显著,垂度效应对竖向动力响应影响较大,梁柱效应的影响较小。
(4)对于沪苏通大桥,当车速为200 km/h,瞬时风速超过35 m/s,或当瞬时风速为30 m/s,车速超过210 km/h 时,车辆轮重减载率指标超出安全阈值,车辆的安全性能受到威胁。
本文的研究成果表明,对于大跨度斜拉桥,几何非线性因素对桥梁结构及桥上列车运行的安全性具有重要的影响,是分析中不可忽视的重要因素。本文对沪苏通大桥开展的多种工况自然风场-车辆-桥梁耦合振动分析,为世界首座跨度超1 km 的公铁两用斜拉桥的安全运营提供了可靠的研究支撑。而沪苏通大桥其复杂的风场环境、大跨度带来的结构非线性,汽车荷载与风-列车-桥梁的耦合作用以及多线行车的荷载工况等多方面的耦合影响,仍有待更丰富的科学研究补充探明。
