中式高耸古木塔风压分布与体型系数风洞试验研究

李雨航，邓 扬，李爱群,，许 涛

(1. 东南大学土木工程学院，南京 211189；2. 北京建筑大学土木与交通工程学院，北京 100044；3. 北京未来城市高精尖创新中心，北京 100044)

中式高耸古木塔是我国建筑文化遗产的重要组成部分，因其结构设计精巧，外形复杂多样而具有极高的历史与文化价值[1]。其中，最具有代表性的高耸古木塔为应县木塔(如图1 所示，其中图1(b)由王贵祥教授团队于1991 年绘制)，其塔高65.84 m，共9 层，由五个明层、四个平座层(又称暗层)及其一个屋顶组合而成，明层与平座层交替建造，增强了木塔抗震与抗风性能[2]。木塔建成于公元1056 年，是我国现存最高、最古老的木塔。然而，木塔长期受到地震与风荷载等作用产生了较大程度的损伤，尤其是风荷载作用，因其具有作用持续时间长，周期重现时间短等特点，使得古木塔风致状态评估成为需要解决的问题。

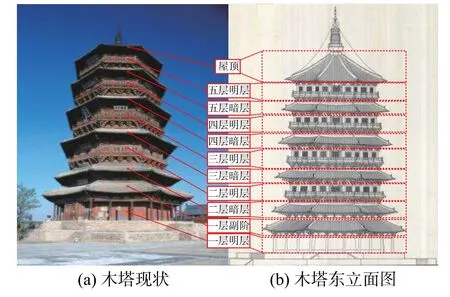
图1 木塔现状及其分区Fig. 1 Zones of wooden pagoda

通过相关研究机构对应县木塔的监测与检测表明，木塔已产生较为严重的倾斜。同时通过现场风环境监测发现，木塔塔址主导风向为西南方向，表明木塔倾斜损伤的持续发展与塔址风作用存在相关性[2]。因此，开展中式古木塔风压分布的全面研究是十分必要的。

目前，研究风压分布的方法主要为风洞试验、计算流体力学与现场实测。国内外学者针对现代建筑结构开展了大量的研究工作，包括低矮结构风洞试验与体型系数研究[3-4]，高层结构风洞试验与实测[5-6]以及桥梁结构的风振响应研究[7]，本文不予赘述。在中式古建筑风荷载研究方面，吴德伦等[8]、李铁英等[9-11]与单文姗[12]等分别对古木塔、古木殿堂建筑进行了风洞试验与风振分析的研究。杨声虎[13]与李雨航等[14]采用CFD技术分别研究了唐代殿堂式建筑与高耸古木塔的风压分布规律。王林安等[15]对应县木塔开展了风荷载与塔址的风环境实测研究。然而，现有研究仍有不足，主要表现在：1)对古建筑抗风安全性能的关注较低，尤其是针对此类具有复杂外形的高耸古木塔的研究较少，尚难以精细刻画其风荷载分布规律，而风荷载分布特性又是风振、风致损伤与木塔振动控制研究的重要前提；2)风荷载体型系数是衡量稳定风压在建筑物表面的分布情况的重要指标之一，其主要与建筑物外形尺度有关[16-18]。体型系数的确定，有助于应县木塔及其类似高耸木塔结构的风荷载计算与保护；3)现场实测是较为准确直接的一种计算风荷载的方法[19-20]，但主要缺点在于受天气、成本与建筑本身的影响较大[21-22]。由于中式古木塔外形复杂，具有较多的挑檐、重檐[23]，所以有限的现场实测测点能否把握住复杂中式高耸木塔整体的风压分布特性与每层风荷载是需要进一步探究的。

本文开展了1∶50 应县木塔精细化刚性模型的风洞测压试验，研究了应县木塔表面的风压特性及其分布规律，并计算了木塔各区域体型系数。采用风洞试验结果计算了木塔的风荷载层间力与层倾覆弯矩，并与实测结果进行了对比。本文旨在通过风洞试验全面深入的研究应县木塔的风压分布特性与规律，同时与现场实测进行互补，为应县木塔的保护提供基础，也为具有类似特殊复杂外形的中式高耸古木建筑的保护与修缮提供参考。

1 风洞试验概况

1.1 试验模型

风洞测压试验在长沙理工大学风洞试验室高速试验段中进行。因木塔结构高宽比相比现代高耸结构小很多，且体型庞大，主体风振效应不明显，故采用刚性测压模型进行研究。基于风洞试验室条件，试验模型采用1∶50 的几何缩尺比，模型总高度为1.32 m，采用松木材质制作，模型如图2 所示，对比图1、图2 可见，该缩尺模型较完备的复刻了应县木塔的外形结构特征，廊柱、栏杆、门窗、斗拱、屋檐及宝顶等区域均按照比例进行精细制作，在风洞试验中将木塔门窗封闭[14]。经计算，模型在风洞中的最大阻塞比为4.5%，小于5%，满足风洞试验要求[24]。

图2 风洞试验模型Fig. 2 Wind tunnel test model

1.2 试验风场

根据木塔所在区域，确定其地面粗糙度指数α=0.15[25]。通过在风洞试验段入口处设置劈尖，在试验段内设置粗糙元，使风场达到规范要求[24]。在风洞转盘中心处测得的风场平均风速与湍流度如图3 所示，图3 中曲线与散点分别为规范理论值与风洞试验值，误差满足试验要求[26]。风洞试验参考点高度为1 m(相当于实际50 m 高度)，该处的脉动风速功率谱密度与Von Karman风速谱的对比如图4 所示[26]，从图4 中可以看出，两者吻合较好，满足试验要求。

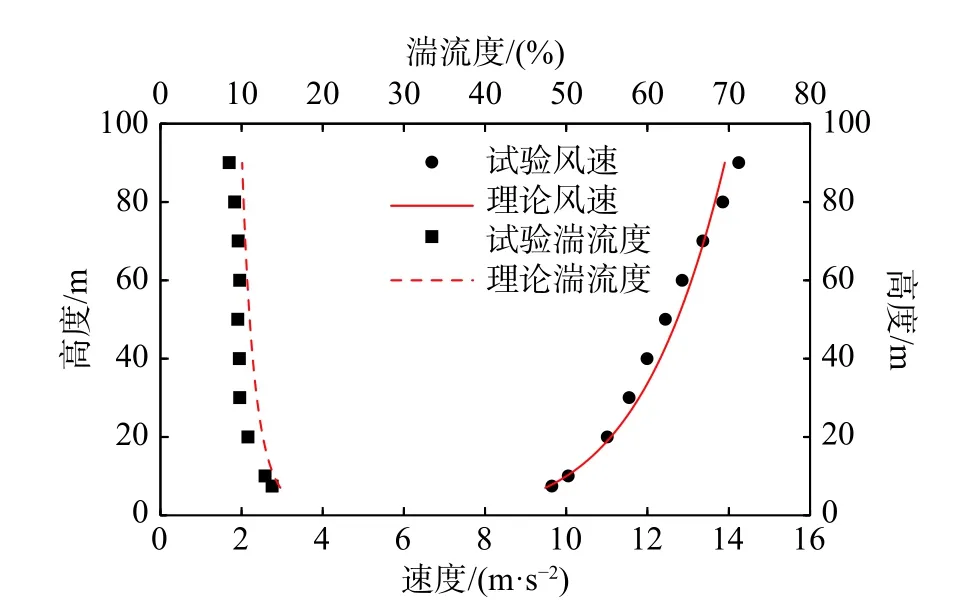
图3 平均风速与湍流度剖面Fig. 3 Mean wind velocity and turbulence intensity profiles

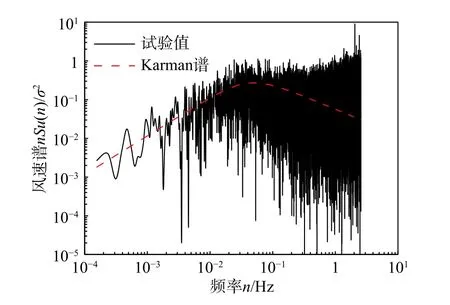
图4 风场1 m 处的风速功率谱密度Fig. 4 Velocity spectra at 1 m height

1.3 测试系统与测点布置

如图5 所示，木塔平面呈现正八边形，因此选取木塔五个面布置风压测点，为①号面～⑤号面。0°风向角为来流风向与①号面正交，风向角按逆时针方向增加，从-45°～45°，变化间隔为11.25°，共开展了9 个工况的试验。

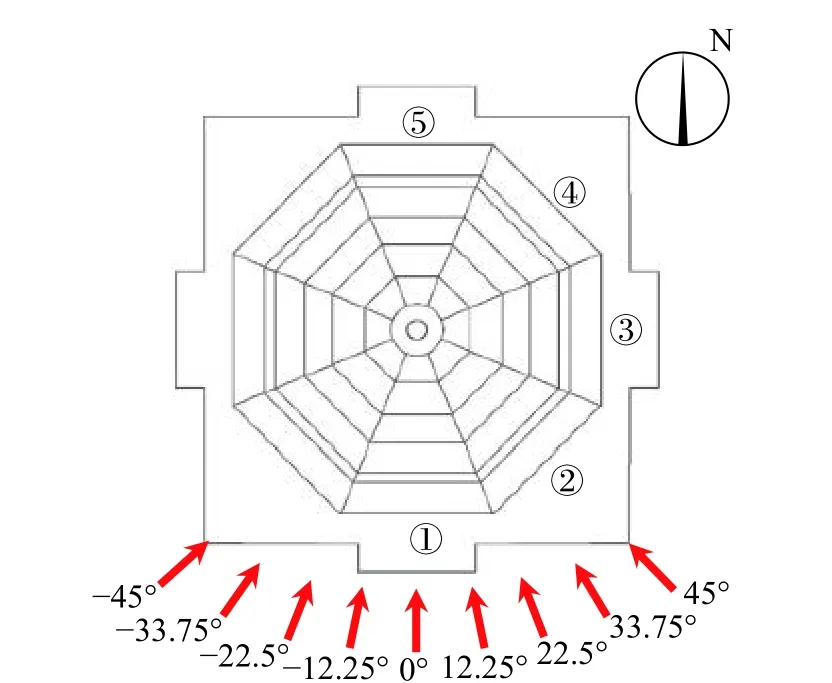
图5 风向角示意图Fig. 5 Diagram of wind directions

风压测点布置如图6 所示，图6 仅给出了图5中①号测点面的测点布置情况，其余面的测点位置及数量与①号测点面相同[14]。根据古木塔的建筑特征，沿高度分为11 个区域，分别为一层门窗墙面(A 区域)、一层副阶及屋檐(B 区域)、二层平座层及屋檐(C 区域)、二层门窗(D 区域)、三层平座层及屋檐(E 区域)、三层门窗(F 区域)、四层平座层及屋檐(G 区域)、四层门窗(H 区域)、五层平座层及屋檐(I 区域)、五层门窗(J 区域)、屋顶(K 区域)。

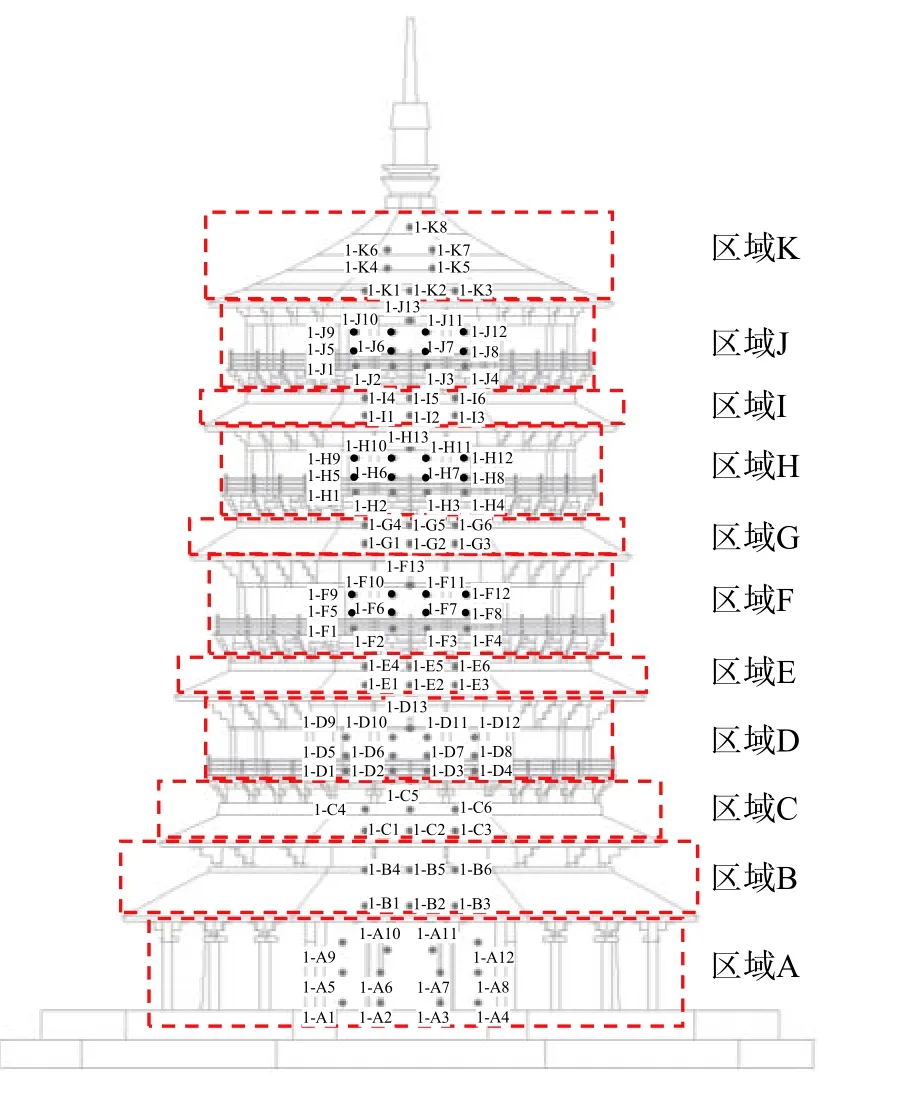
图6 木塔风压测点布置Fig. 6 Pressure taps on wooden pagoda

其中：A 区域布置12 个测点；D 区域、F 区域、H 区域和J 区域各布置13 个测点；B 区域、C 区域、E 区域、G 区域和I 区域各布置6 个测点；K 区域布置8 个测点；屋檐区域的测点均布置在屋檐上表面，距离屋檐边缘20 mm。每个面的风压测点数量为102 个，整个模型为510 个。图6 中测点编号规则为“测点面编号+区域号+测点编号”。

1.4 数据处理

由风洞试验获取脉动风压，并在输出数据时进行测压管畸变修正[27-28]。0.2 m 高度处(实际10 m 高度处)的风速为10 m/s，根据几何与风速缩尺比，采样频率选定为200 Hz，采样时间为60 s[29-30]，约为原型结构的10 min。使用修正后的风压时程数据可计算每个测压点i的瞬时风压系数Cpi(t)为[31-32]：

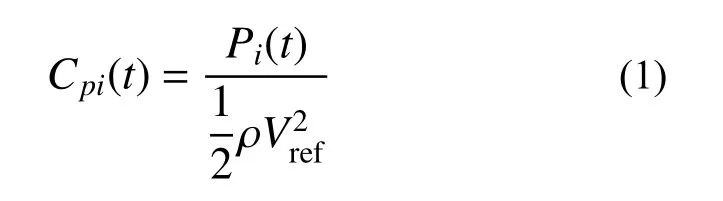
式中：Pi(t)为t时测得的测压点i的压力；ρ 为空气的密度，可取1.225 kg/m3；Vref为参考高度处的风速。规定风压系数为正时，结构所受风压力，反之为风吸力。

2 木塔平均风压系数计算结果

因木塔结构较为复杂，故将木塔的风荷载特性结果分为两个部分进行阐述，分别为门窗墙面区域(明层区域)和各层平座层及屋檐区域(暗层区域)。其中门窗墙面区域包括图6 中A 区域、D 区域、F 区域、H 区域与J 区域，他们的外形特征为正八边形，且与楼面垂直。而各层屋檐及其屋顶区域包括B 区域、C 区域、E 区域、G 区域、I 区域与K 区域，其主要特点为有较大屋顶，且屋顶具有较大的挑檐，它与现代结构相差较大。对式(1)计算出的测点i下的风压系数取平均值，得到净平均风压系数。各面在0°风向角作用下平均风压等值线图如图7 所示。

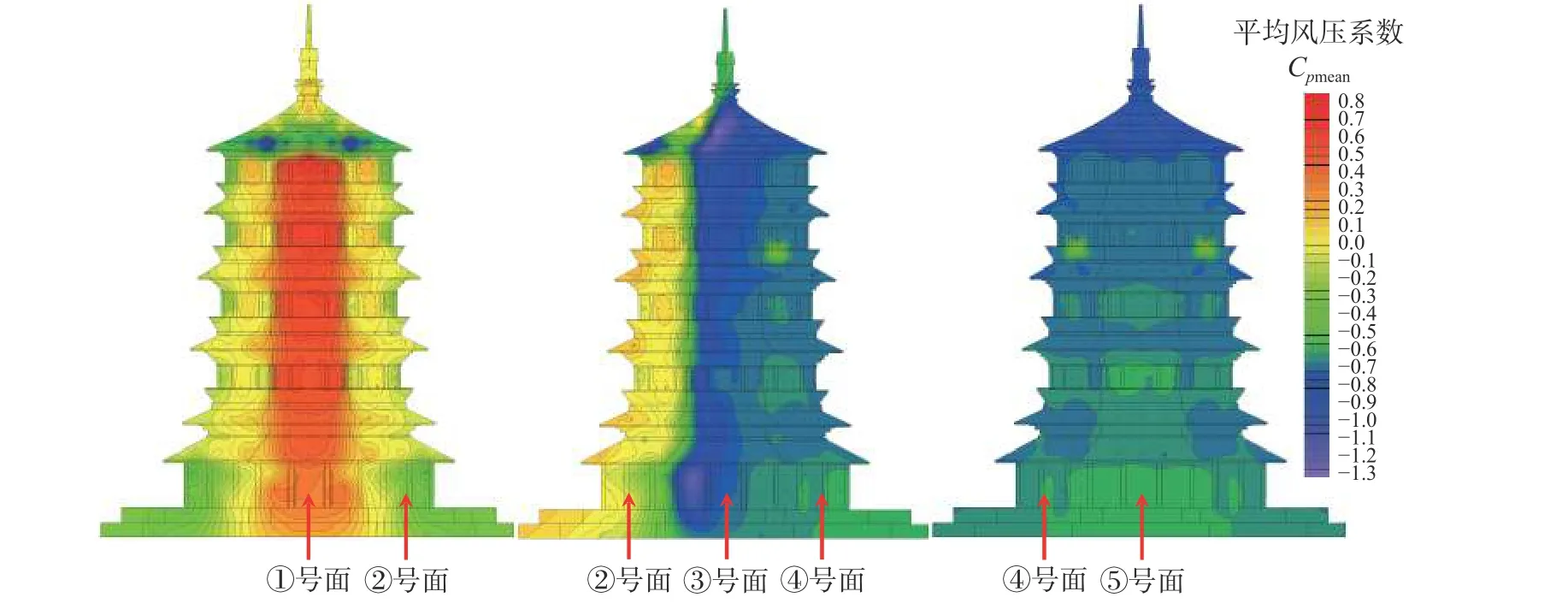
图7 各面在0°风向角下平均风压等值线Fig. 7 Contour plots of mean pressure coefficients at wind direction of 0°

2.1 门窗区域

如图7 所示，①号面上的门窗墙面受风压力，风压系数最大值出现在中部偏上处(H 区域与J 区域)，数值可达0.7，这与普通矩形建筑风压系数趋势类似。在②号面上风压分布从风压力转变为风吸力，说明此时风已发生了分离。在侧风面③靠近迎风面处出现了较大的风吸力，风压系数超过-0.6。其中，因有一层副阶影响，横截面变小，风速变快，一层走廊墙面(A 区域)风压系数绝对值可达到1.2。④号面与⑤号面均受风吸力，因风回旋较小，故风压系数几乎不产生变化，这与外形为矩形的现代结构的风压分布趋势具有一定相似性。

不同位置的测点在不同风向角工况作用下的风压系数均有所不同，因篇幅有限，选取四层门窗墙面区域中部层测点(H5 点～H8 点所在平面层)进行分析，该区域内测点在不同风向角工况下的平均风压系数如图8 所示。由于木塔以45°为一对称轴，所以可以从图8 中看出-45°、0°与45°的风压分布是几乎一样的，只是相差了一个平面的距离，这也验证了风洞试验的准确性。在迎风面①上，当风向角在-22.5°～22.5°变化时，四层门窗测点风压系数受风向角影响较小；当风向角大于22.5°或小于-22.5°时，迎风面风压系数变化明显，逐步由风压力转为风吸力。值得注意的是，当风向角在-22.5°～22.5°变化时，位于区域中间位置测点(H6 点与H7 点)的风压系数受风向角的变化影响较小，而位于区域两侧位置的测点(H5 点与H8 点)受风向角的变化影响较大，说明突出的结构角柱对结构风压系数有一定的干扰作用。在②号面上，随着风向角的增大，风压系数也随之增大。在侧风面③上，当风向角在-22.5°～22.5°变化时，风压系数变化较小，且风上游处风压系数比风下游处风压系数的绝对值大，主要原因在于风在②号面与③号面的转角处产生了分离，致使转角处的风吸力变大；当风向角大于22.5°时，风压系数变大直至变为正值。在④号面与⑤号面上，风压系数随着风向角变化幅度较小，风压系数绝对值为0.650左右，主要原因在于木塔宽度较大，风不易产生回流。

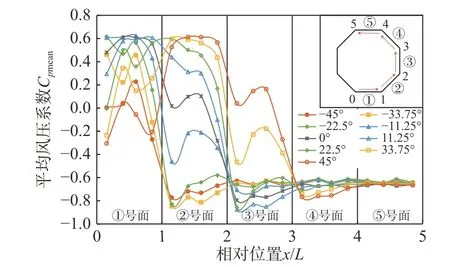
图8 四层门窗区域中部测点在不同风向角下的风压系数Fig. 8 Mean pressure coefficients at the middle layer of the 4th wall zone under different wind directions

2.2 屋檐区域

大屋檐是中国古代木结构的主要特点之一，具有结构复杂，规模庞大等特点，也是古木建筑保护的重要部分。而应县木塔具有多重屋檐，且每一层都具有不同形式，这就使得风在每层屋檐的变化不尽相同，也给木塔的保护造成了新的难题，本节主要介绍木塔风洞试验中各层屋檐尤其是顶层屋檐的风压系数。为进一步研究木塔大屋顶的风压变化，将屋顶层的风压系数单独提取出来，其云图如图9 所示。

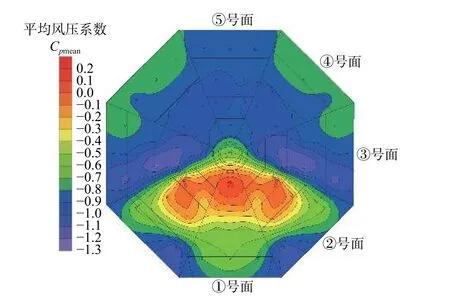
图9 顶层屋檐平均风压等值线图Fig. 9 Contour plots of mean pressure coefficients on the top roof at 0° wind direction

从图7 与图9 可以看出，迎风面①上第1 层～第5 层屋檐(B 区域、C 区域、E 区域、G 区域、I 区域)受风压力，这是因为屋檐上部还有新的一层，会受到周围斗拱与栏杆等构件的影响，使得风没有产生分离现象，这与现代建筑屋檐完全不同；其他面上的第1 层～第5 层屋檐平均风压系数与墙面风压系数趋势相似。在屋顶层上，迎风侧宝塔尖顶下方的一小块区域达到0.200，这是因为风流场被宝塔顶点所阻挡。在②号面上，靠近上游风的屋顶(E1 点和G1 点)产生最大的正风压系数，数值可达+0.173，这与门窗区域的风压系数相似。在屋顶区域，靠近风上游区域的绝对风压大于风下游区域的绝对风压，最小风压系数达到-1.090。在③号面上，整个屋檐区域均受较大风吸力，风压绝对值在上游区域大于下游区域，屋顶会产生最大的平均压力，其值为-1.220。在④号面与⑤号面上，整个区域均受到风吸力的作用，其压力系数稳定在-0.599～-0.707。

通过对不同风向角作用下的屋顶区域边缘层测点(K1 点～K3 点所在平面层)进行分析可以得出(图10)，屋顶测点在不同风向角作用下均为负值，产生较大的风吸力。在迎风面①上屋顶中间区域测点(K2 点)受风向角的变化影响较小，而边缘测点(K1 点与K3 点)影响较大，最大增幅可达70%。同样的，在②号面～④号面平面上由于屋顶形状复杂，测点风压对风向角极其敏感，尤其在②号面上，其变化率可达到100%。同时从图10 中可以看出，风上游的压力测点比风下游的压力测点对风向角更为敏感，这是因为屋顶处有屋脊的阻挡，会扰动来流的风。背风面⑤上风压测点的风压系数受风向角变化影响较小，其变化幅值小于15%，其原因在于⑤号面距离风场加速区较远，受风分离作用的影响较小。

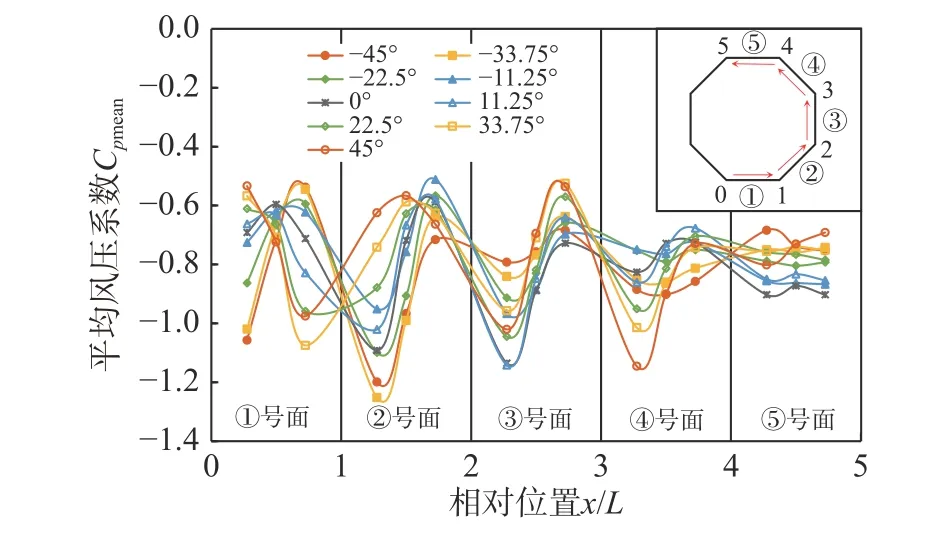
图10 五层屋檐区域边界测点在不同风向角作用下风压系数Fig. 10 Mean pressure coefficients at the boundary layer of the 5th roof under different wind directions

2.3 木塔体型系数的计算

风压系数可一定程度上反映木塔风压分布特性，但无法直接与其他建筑进行比较。而体型系数反应建筑物体型与尺度，可较为直观地与不同建筑进行比较，也可直接的用于应县木塔的风荷载计算与保护及其相似建筑的设计。

荷载规范规定测点体型系数为该点产生的表面风压与来流风的速度压之比。故通过式(1)计算出的风压需要将其中的参考风速换算为测点高度处的来流速度才可以计算出木塔每个测点的体型系数。在得到各测点体型系数后，按式(2)将每个区域上每个测点的体型系数按照所属面积进行加权平均，可得到每个区域面上的体型系数[31]。

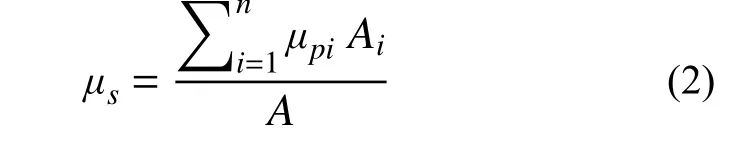
式中：μpi为i测点的体型系数；Ai为i测点附属面积；A为各区域所有测点的总面积。

根据式(2)计算出图6 中每个墙面与屋面区域面的平均体型系数分别如图11 所示。从图11 计算出的风洞试验结果可以看出：①号面体型系数为正值，系数随结构高度变化较小，其平均值为+0.634。②号面上，一层门窗区域(A 区域)为负值，说明此处风速较快，产生了风吸力。而整体门窗区域体型系数平均值为-0.116。③号面上各层体型系数均为负值，其中A 区域体型系数绝对值最大，是其他区域的1.7 倍左右。其他区域随高度变化不大，说明木塔侧风面受建筑性质影响较大，其一层副阶走廊区域会使风速加快，使得系数增大。在④号面与⑤号面上，体型系数相差不大，分别为-0.866 与-0.839，且沿高度变化较小。

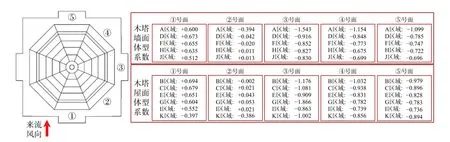
图11 风洞试验计算出的门窗墙面与屋面区域体型系数Fig. 11 The shape factors for the walls and roofs of the pagoda model calculated by the wind tunnel test

而通过对每层屋檐的体型系数的计算与分析可以得出：除顶层屋檐外的各个屋檐体型系数与门窗区域类似，数值均随高度的增加而减小，但变化幅度较小。较为特殊的是屋顶区域，整个屋顶区域体型系数均为负值，①号面与②号面数值相同，在③号面达到最大，主要原因为塔尖在中间起到了阻挡作用，导致风绕流引起变化。

3 风荷载计算及其与实测结果的对比

2011 年中国文化遗产研究院进行了木塔风荷载与风效应原型实测[2,20]，确定了木塔周边的风场特性与木塔表面的风荷载分布规律，并计算出了风荷载作用下结构基底剪力与弯矩。由于木塔周边环境复杂，木塔表面实测的风压系数影响因素较多，不易准确反映木塔表面每个测点的风压状况，故通过计算每个点的实测风压系数获得每层的风荷载，进而得到风荷载层间力。同时，采用相同方法对风洞试验下的结果进行计算，并将结构层间力与实测结果进行对比。

3.1 风荷载计算方法及其结果

风荷载可以通过实际压力和实际高度来计算。风荷载分区示意图如图6 所示，与测点分布区域一样，具体为：将木塔分为11 个区域，其中A 区域、D 区域、F 区域、H 区域、J 区域分别为第1 层～第5 层的明层；B 区域、C 区域、E 区域、G 区域与I 区域为副阶；第2 层～第5 层的平座层与屋檐，K 区域为屋顶层。风荷载包括风层间力与风倾覆弯矩，分别定义为：

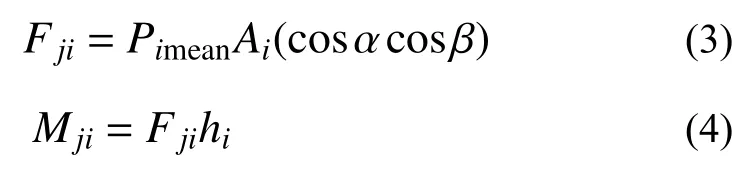
式中：Fji与Mji为在j层中i测点的风荷载力与倾覆弯矩(应县木塔包括五个明层、四个平座层、一个副阶屋檐与一个顶层屋檐)；Pimean为测点i的风洞试验平均风压数值；Ai为测点i的子区域面积；α 和β 为测点i所在的表面的法线和风向之间的水平与竖直夹角；hi为测点i的模型高度。

风荷载层间力与倾覆弯矩Fj和Mj可以表示为：

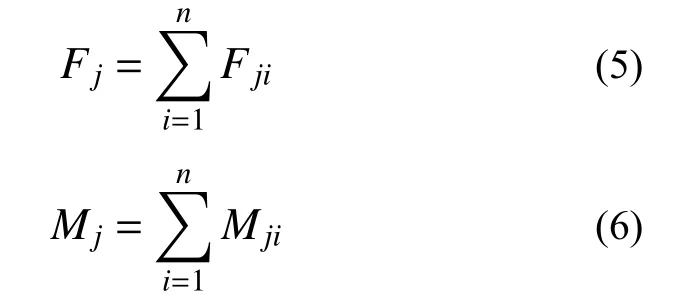
式中，n为j楼层上的压力测点的数量。

木塔模型在三个风向角(-22.5°、0°和22.5°)下的风荷载层间力如表1 所示。从表1 中可以看出随着模型高度的增加，风荷载层间力减小。除了A 区域外，明层层间力要大于对应平座层层间力。一层明层层间力小于一层平座层层间力的原因在于平座层部分所属面积较大，在第一层副阶区域出现最大风荷载层间力为4.64 N。最大基底剪力在0°风向角下为40.04 N，大于在-22.5°与22.5°风向角下的35.5 N 与34.7 N。随着高度的增加，层倾覆弯矩会有所增加，除A 区域外，明层的层倾覆弯矩大于平座层的层倾覆弯矩，这与风荷载层间力趋势类似。在J 区域出现最大层间倾覆弯矩为3.38 N·m，0°方向角下基底倾覆力矩为21.15 N·m，比-22.5°与22.5°下的层倾覆力矩大15.6%。

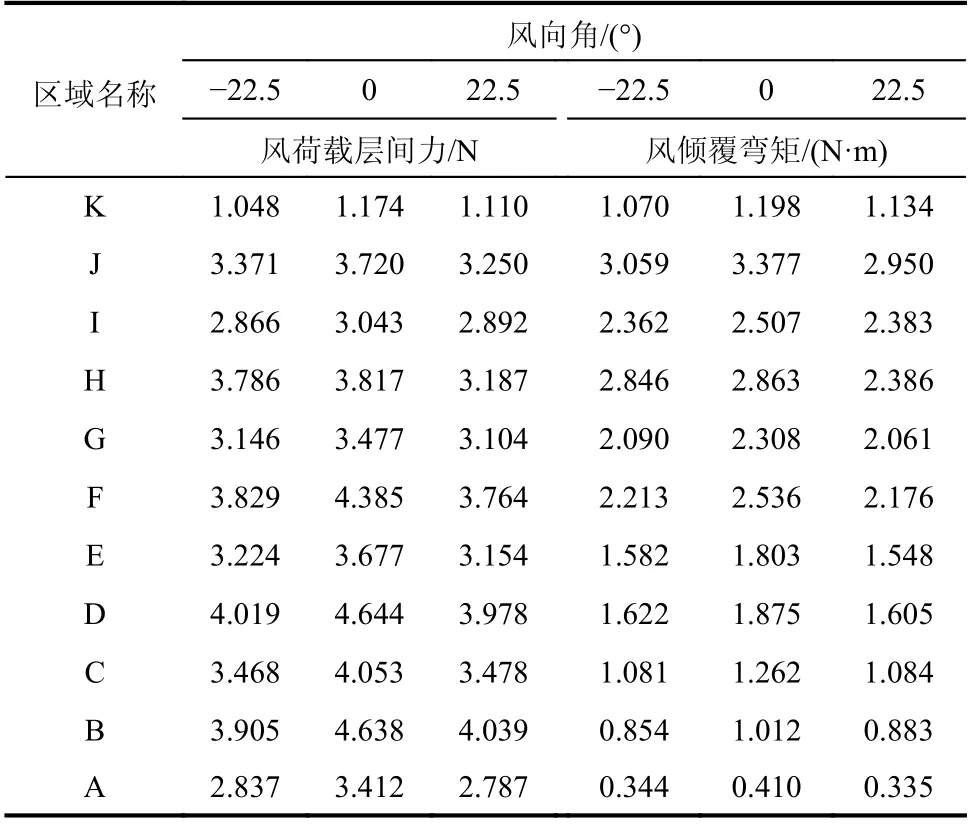
表1 木塔模型在-22.5°、0°与22.5°下的风荷载层间力与层倾覆弯矩Table 1 Wind story force and story overturning moment of pagoda model under -22.5°, 0° and 22.5°

3.2 与实测结果的对比

通过公式的计算可得实测结果的风荷载层间力，由于实测计算出的风压系数与测试中风环境风向有较大关系，进而计算出的木塔体型系数也会与风向有很大联系。经过计算发现实测结果层间力与22.5°风向角下的结果较为相近，层间力与层倾覆弯矩对比如图12 所示。其中风洞试验中的风荷载层间力需要根据缩尺比与风速比进行换算，需要说明的是图中层间力与层倾覆弯矩为在实际测试中10 m 高度处27.1 m/s 风速时的计算数值。从图12 中可以看出两者的风荷载层间力趋势大致相同，都随高度的增加而减小。经过计算对比可知，风洞试验的基底剪力为638.1 kN，而实测的基底剪力为560.3 kN，两者相差13.9%，也验证了两者的趋势相同。实测中的风荷载层间力在大多数楼层上比风洞试验小，这主要是因为木塔的一部分构件如上窗等是透风的，导致整体风压系数偏小，进而计算出的层间力较小。同样地，层间倾覆弯矩的趋势与层间力大致相同，其基底倾覆弯矩分别为，风洞试验17031.0 kN·m，而实测结果为15098.3 kN·m，两者相差12.8%，相差较小。由于实测受到诸多限制，例如监测测点较少，费用较高，环境因素复杂等问题，无法十分准确地反应木塔风荷载特性，尤其是在复杂的屋檐区域，此时还需要风洞试验来确定木塔的风荷载特性。

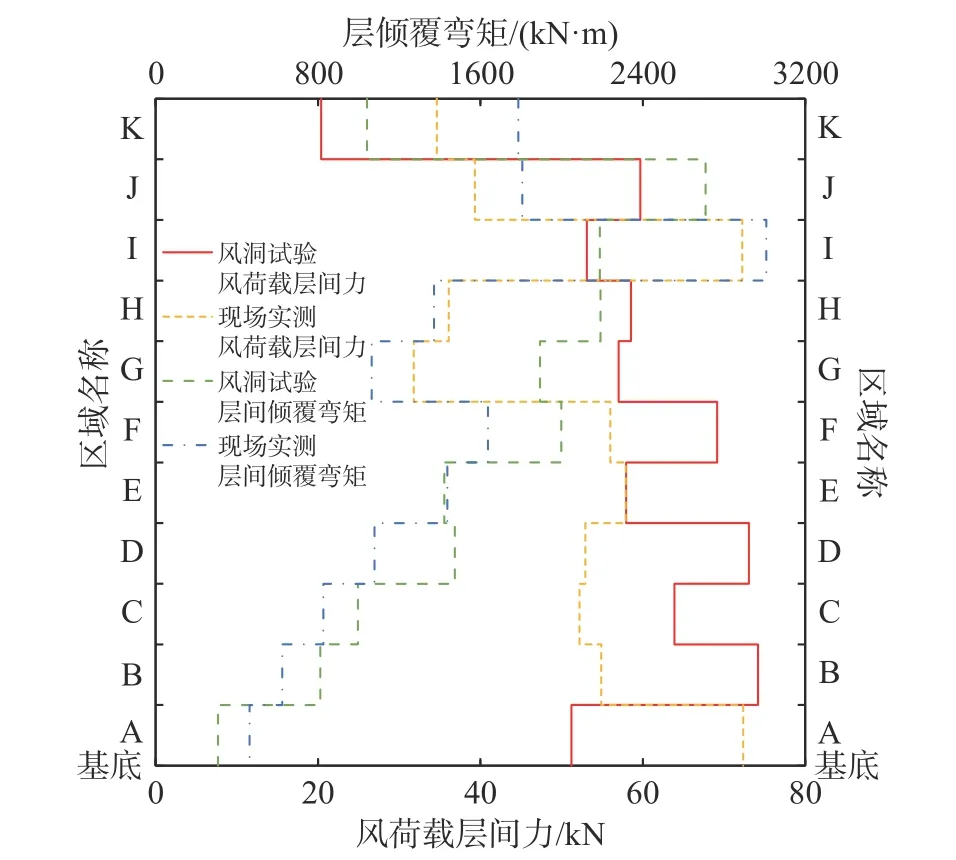
图12 试验与实测的风荷载层间力与倾覆弯矩对比Fig. 12 Comparisons of story forces and overturning moments under wind action between test and measuring field

4 结论

基于1∶50 缩尺比的应县木塔刚性模型，开展了风洞测压试验，研究了木塔表面的风压特性与典型测点在不同风向角作用下的分布规律。从墙面与屋檐两个角度计算了木塔各区域体型系数。采用风洞试验结果计算了木塔的风荷载层间力与层倾覆弯矩，并与实测结果进行了对比，研究结论如下：

(1)风洞试验中木塔墙面区域的迎风面会出现风压力，最大风压力出现在中部偏上区域(H 区域)；在②号面上风压分布从风压力(正值)变化为风吸力(负值)；③号面区域产生较大风吸力，且离迎风面越近，风压系数绝对值越大；④号面与⑤号面产生较大风吸力，但各区域数值变化较小。①号面1 层～5 层屋檐受到风压力，且数值与门窗墙面区域基本相同；屋顶屋檐上，仅在塔尖正下方的一小块区域产生风压力，其余均为风吸力。②号面与③号面上，风压绝对值在上游区域大于下游区域。在④号面与⑤号面上，整个区域均受到风吸力的作用，风压系数较为稳定。

(2)通过计算，获得木塔的体型系数，除屋顶屋檐外，各区域随着木塔高度增大，体型系数均有所减小。且门窗区域体型系数与屋檐体型系数趋势与数值大致相同。A 区域因有副阶的影响而有所不同，在②号面上表现为明显风吸力，同时在③号面～⑤号面上具有比其他各层大的风吸力。屋顶区域因有塔尖的阻挡作用，使得其整个区域体型系数均为负值，与其他各层的数值有较大不同。

(3)风洞试验计算出的层间力随着木塔模型高度的增加而减小，而风荷载层倾覆弯矩随着木塔模型高度的增加而增大；除了第一层(A 区域与B 区域)外，风洞试验计算出的木塔明层风荷载层间力与层倾覆弯矩要大于对应平座层的风荷载层间力与层倾覆弯矩；在0°风向角作用下的层间力与倾覆弯矩要大于-22.5°与22.5°风向角作用下的风荷载。经过与实测数据的比对，风洞试验计算的风荷载层间力与倾覆弯矩与实测结果沿高度变化趋势大致相同，基底剪力与基底倾覆弯矩误差均在13%左右，相差较小。但因实测的场地多变与建筑物外形复杂而无法准确反映木塔风荷载分布特性，实测中的风荷载层间力在大多数楼层上比风洞试验小，此时还需要风洞试验来进行补充与验证。本文研究成果可为应县木塔风致损伤、安全性评估与保护提供基础。