高变形能力螺栓抗剪连接件抗剪承载力理论分析与验证

齐连训，罗云标,2，严加宝,2，林旭川

(1. 天津大学建筑工程学院，天津 300350；2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300350；3. 中国地震局地震工程与工程振动重点实验室，黑龙江，哈尔滨 150080)

由于充分发挥了混凝土抗压和钢材抗拉性能好的优势，钢-混凝土组合梁等新的组合构件在桥梁和建筑结构领域得到了广泛的应用。这些构件中使用的抗剪连接件提高了两者的组合作用，其中焊接栓钉是已有的抗剪连接件中应用最普遍的一种，其基本力学性能得到了深入而广泛的研究[1-2]。近年来，随着可持续、资源有效和低碳的循环经济目标得到越来越多的重视，如何使得结构或构件具备全生命周期可拆卸和重复利用功能，已成为研究的热点[3]。在钢-混凝土组合结构中，使用螺栓替代焊接栓钉作为抗剪连接件，也得到越来越多的研究和实际应用[4]。

虽然螺栓作为抗剪连接件使组合梁具备可拆卸性，但是多位学者[5-9]通过推出试验得出螺栓连接件剪切变形小于或略大于Eurocode 4 规定6 mm限值，变形能力较差，因此有必要采取一定措施增强螺栓抗剪连接件的变形能力。针对传统焊接栓钉抗剪连接件存在变形能力不足的问题，刘玉擎等[10-11]在焊钉杆部外套橡胶构成新型焊钉-橡胶连接件，Han 等[12]则首次将掺加橡胶颗粒的弹性混凝土用于焊钉连接的钢-混组合梁，两位学者采用弱化连接件周围材料的方法来提高连接件变形能力。基于相似的思路，针对螺栓抗剪连接件变形能力较低的问题，本文提出了一种插块式螺栓抗剪连接件(plug-type bolted shear connector, PTBSC)，如图1 所示。这种插块式螺栓抗剪连接件通过锥台式的插块设计，使得螺栓螺杆根部部分区段周围无混凝土包裹，成为预设的集中变形区段。此外，将螺栓抗剪连接件封装成插块形式，便于装配和可拆卸功能的实现。

如图1 所示，PTBSC 由上部的埋固段、螺杆根部的集中变形段和下部的紧固段三部分组成。

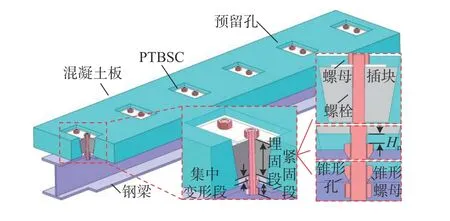
图1 插块式螺栓抗剪连接件细节图Fig. 1 Details of PTBSC

埋固段将混凝土插块和双头螺纹高强螺栓预制成一体，通过插块顶端外露的螺栓螺纹段拧紧螺母，插块整体楔入混凝土板预留孔内且与预留孔孔壁严密贴合，该段可将螺栓承受剪切作用力时对混凝土体的损伤阻断在插块范围内，降低了混凝土板的损伤。

集中变形段是在插块下表面和锥形螺母上表面之间预留了螺栓螺杆的变形区段，因为钢材的变形能力较强，因此这种设置可增强连接件变形能力。

紧固段通过在钢梁翼缘钻设锥台形开孔，并通过部分埋入锥台形开孔的锥形螺母和普通螺母将带螺纹段的穿孔螺杆紧固于钢梁翼缘上，首先由于锥形螺母增大了剪切面接触面积从而减小了作用于钢梁开孔的应力，因此保护了钢梁开孔，其次锥形螺母的使用避免了钢梁的初始滑移问题，也避免螺纹段与钢梁开孔接触造成的螺纹段局部变形，增强了连接件可拆卸性。

本文提出的插块式剪力连接件采用抗压强度大于100 MPa 超高性能混凝土(ultra-high performance concrete, UHPC)作为插块材料，作为保证连接件在发生插块的压溃破坏之前，先发生螺栓集中变形段剪断破坏的构造措施。

为了对PTBSC 的力学性能进行理论评价，本文研究了现有抗剪连接件理论计算公式。针对焊接栓钉连接件[13-18]、新型连接件[19-21]和螺栓连接件[5,22-23]，国内外规范和学者运用统计分析或理论推导的方法给出了抗剪连接件抗剪承载力的计算公式。

本文首先根据初步推出试验和相应的精细化有限元分析，得到PTBSC 的剪切-滑移关系曲线，发现曲线呈现明显的近似双线性。基于PTBSC 的受力机理，提出了其在抗剪承载力屈服状态的理想受力模型，推导出PTBSC 的屈服抗剪承载力的理论计算公式。通过理论计算结果与有限元分析结果的比较，对提出的理论计算公式的准确性进行了验证，并分析了不同参数对PTBSC 屈服抗剪承载力的影响规律，为PTBSC 的工程应用给出了设计建议。最后，通过有限元模拟结果的统计分析，得到了PTBSC 极限抗剪承载力的经验公式。

1 剪切-滑移特性

为研究PTBSC 的基本力学行为和剪切-滑移特性，本文参照Eurocode 4[14]设计了2 组推出试件，并以推出试件为原型建立了相应的ABAQUS 有限元分析模型。

如图2(a)所示，推出试件包括2 块带锥台形预留孔的混凝土板、1 根钻设锥形开孔的H 型钢梁、2 个PTBSC。其中，PTBSC 是由混凝土插块与2 根双头螺纹高强螺栓及其配套的六角螺母和适配于钢梁开孔的锥形螺母组成。在推出试件顶部使用位移控制进行加载，加载速率为0.5 mm/min，过螺栓水平面位置设有4 个位移计，用于测量推出试件四个高强螺栓的相对滑移s，顶端竖向荷载通过液压机内置力传感器读取，单个螺栓所承受剪力P取顶端施加荷载的1/4。如图2(b)所示，以所制作推出试件为原型建立了推出试件的ABAQUS有限元模型并进行网格划分。模型中的不同部件(H 型钢、螺栓、插块和混凝土板等)间的相互关系如下：不同部件之间采用面面接触(surface-tosurface)，接触关系定义中切向采用罚函数，法向采用硬接触来模拟，钢材与钢材、钢材与混凝土之间的摩擦系数分别取为0.3、0.25；钢筋骨架与混凝土板的相互关系则采用嵌入关系进行模拟。采用动态显式进行有限元分析，分析结果获取方法与推出试验相同。

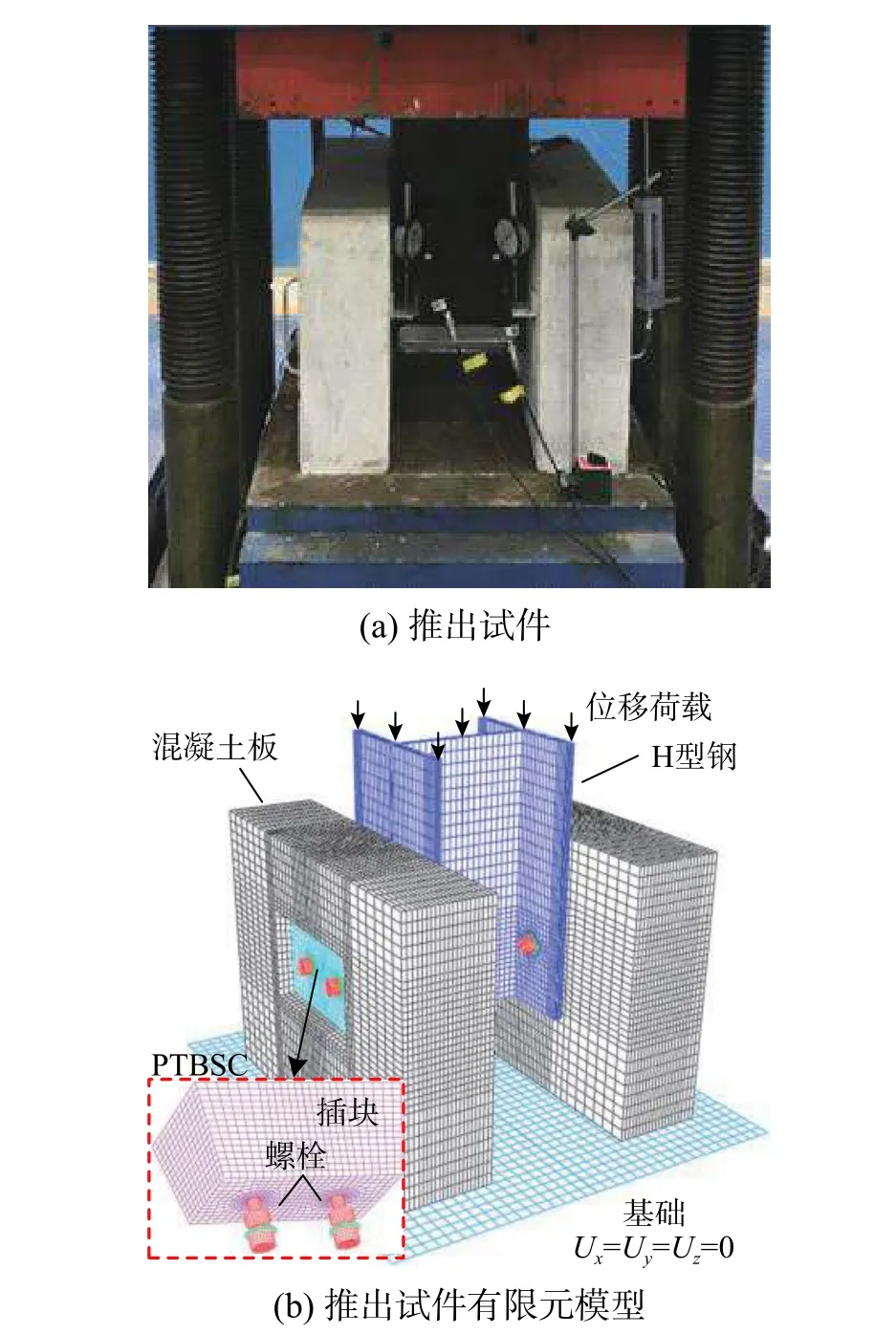
图2 推出试件原型试验及有限元模型Fig. 2 Push-out specimen prototype test and FEM

图3 为分别采用M14 和M18 螺栓的两组PTBSC 试验及有限元分析中的破坏模式对照图。推出试验和对应的有限元分析发生的破坏模式均为螺栓集中变形段剪断破坏，且集中变形段均表现出较好的变形能力，验证了PTBSC 的设计破坏模式，同时表明有限元模型可再现PTBSC 的破坏模式。

图3 试验和有限元PTBSC 破坏模式Fig. 3 Failure mode of test and FEA for PTBSC

图4 为分别采用M14 和M18 螺栓的两组PTBSC，以及普通M14 螺栓[24]的剪切-滑移曲线的推出试验结果及有限元模拟结果。将有限元曲线与试验曲线对比可以发现，其屈服荷载和极限荷载的误差在12%以内，有限元模型可较好地模拟出PTBSC 的剪切-滑移行为。其次，有限元分析曲线和推出试验曲线的曲线形状均表明PTBSC 的剪切-滑移关系曲线存在明显的屈服点和极限点，曲线呈现出近似双线性特征。同时，曲线有较大的屈服后刚度(为初始刚度的1/3～1/2)，以及较大的屈服后承载力储备(极限承载力接近2 倍的屈服承载力)。最后，对比表明，PTBSC 在相同直径的条件下，其极限抗剪承载力与普通螺栓相当，而变形能力则远大于普通螺栓抗剪连接件。

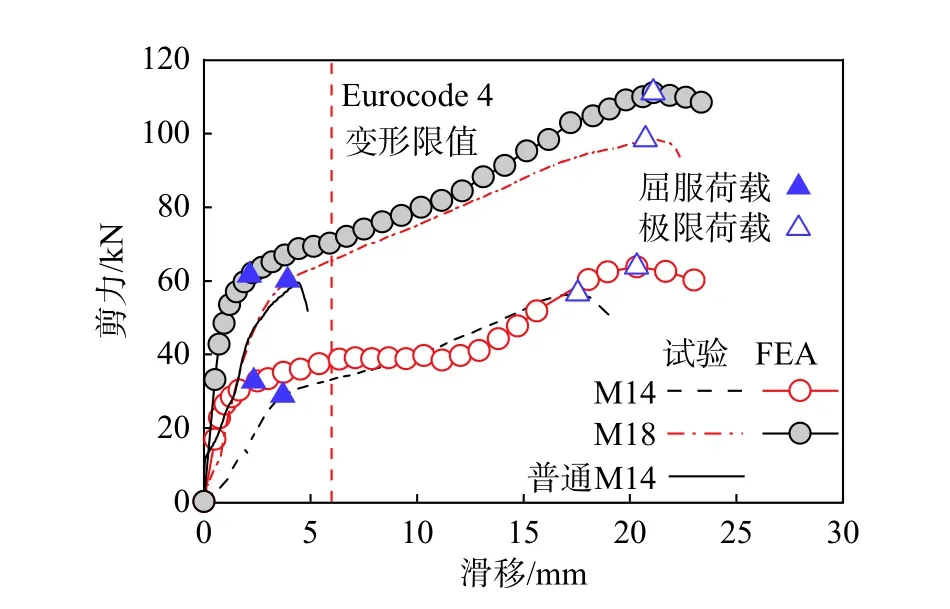
图4 试验和有限元PTBSC 剪切-滑移曲线Fig. 4 Load-slip curve for PTBSC of tests and FEA

如图5 所示，对剪切-滑移曲线近似为双线性关系。其中，屈服抗剪承载力Py参考冯鹏等[25]提出的“最远点法”来确定，极限抗剪承载力Pu则取为剪切-滑移关系曲线的峰值点。

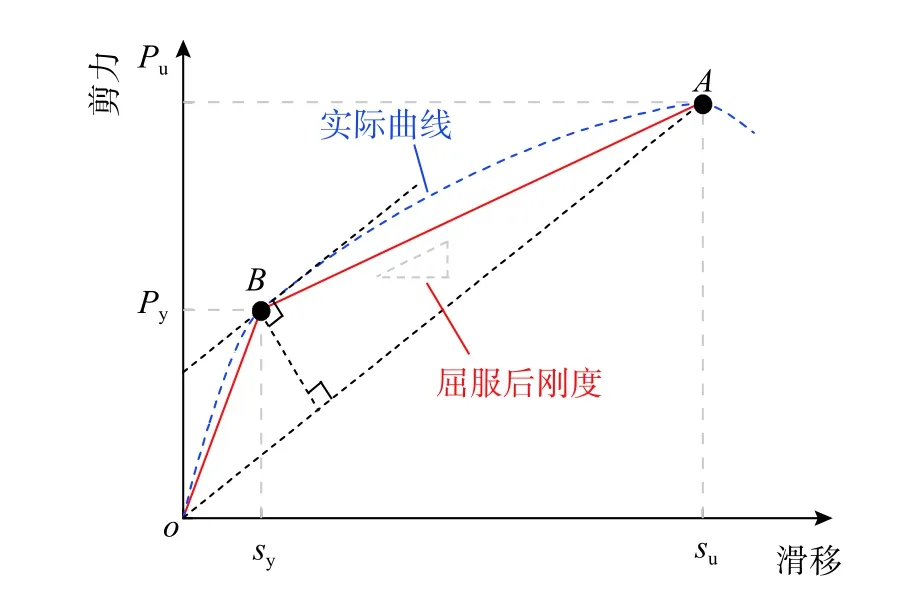
图5 典型的PTBSC 剪切-滑移关系曲线Fig. 5 Characterized shear-slip relationship curve of PTBSC

为便于对采用PTBSC 的组合构件进行设计，需要在理论分析的基础上建立其Py和Pu相应预测和计算方法。

2 屈服抗剪承载力的理论分析

2.1 屈服抗剪承载力的理论推导

屈服抗剪承载力Py是抗剪连接件力学性能的关键指标，常用的焊接栓钉抗剪连接件的剪切-滑移关系曲线中并无明显的屈服点，通常基于其极限抗剪承载力按一定取值方法来确定。本文提出的PTBSC 的剪切-滑移关系曲线具有明显的屈服点，因此，本节根据其屈服时对应的受力状态，通过理论推导的方式，确定其屈服抗剪承载力。

为简化受力状态的分析，对PTBSC 力学模型作理想化假设如下：

1) PTBSC 在工作荷载下的力学性能符合弹塑性理论，该理论认为PTBSC 中的高强螺栓是一个均质的理想弹塑性部件，PTBSC 中插块材料是一种均质的理想弹塑性材料。

2) PTBSC 各部分在工作荷载下的变形满足变形协调原理。

3) PTBSC 中插块材料具有足够高的强度，以避免在各种外力的共同作用下PTBSC 中的插块的完全压溃。

4) PTBSC 中螺栓在剪力作用下的变形应在满足部件正常工作的范围内。锥形螺母和钢梁翼缘锥形孔、插块和预留孔均始终严密贴合，锥形螺母未发生相对于锥形孔的相对位移。

由于本文所提PTBSC 受力机理与埋置在粘性土中的桩头被约束桩的受力状态类似，因此借鉴Broms[26]对于桩基水平承载力的理论推导方法对PTBSC 屈服抗剪承载力理论公式进行推导。

选取如图6(a)所示的单个PTBSC 作为分析原型，对其进行受力简化如图6(b)所示。螺栓上侧插块上表面位置边界条件简化为固端支座，螺栓下侧锥形螺母上表面位置边界条件简化为滑动支座，埋固段螺栓简化为直径D0的光滑螺杆，集中变形段螺栓简化为直径Dn(螺纹段螺栓最小截面直径)的光滑螺杆，插块简化为与混凝土板固结的混凝土体，其中滑动支座处承受垂直于螺杆轴线的剪力P。

PTBSC 在受剪力作用时螺杆对插块混凝土体产生挤压变形，并产生反作用力。如图6(c)所示，随着剪力P增大，长度为Hn集中变形段在锥形螺母上表面处(即最大负弯矩处)形成塑性铰C；随后，埋固段螺栓距离插块下表面Hy的最大正弯矩处也形成塑性铰D，螺栓两个塑性铰C和塑性铰D处的弯矩值分别为对应螺栓截面的屈服弯矩。此时，抗剪连接件PTBSC 达到其屈服抗剪承载力Py。

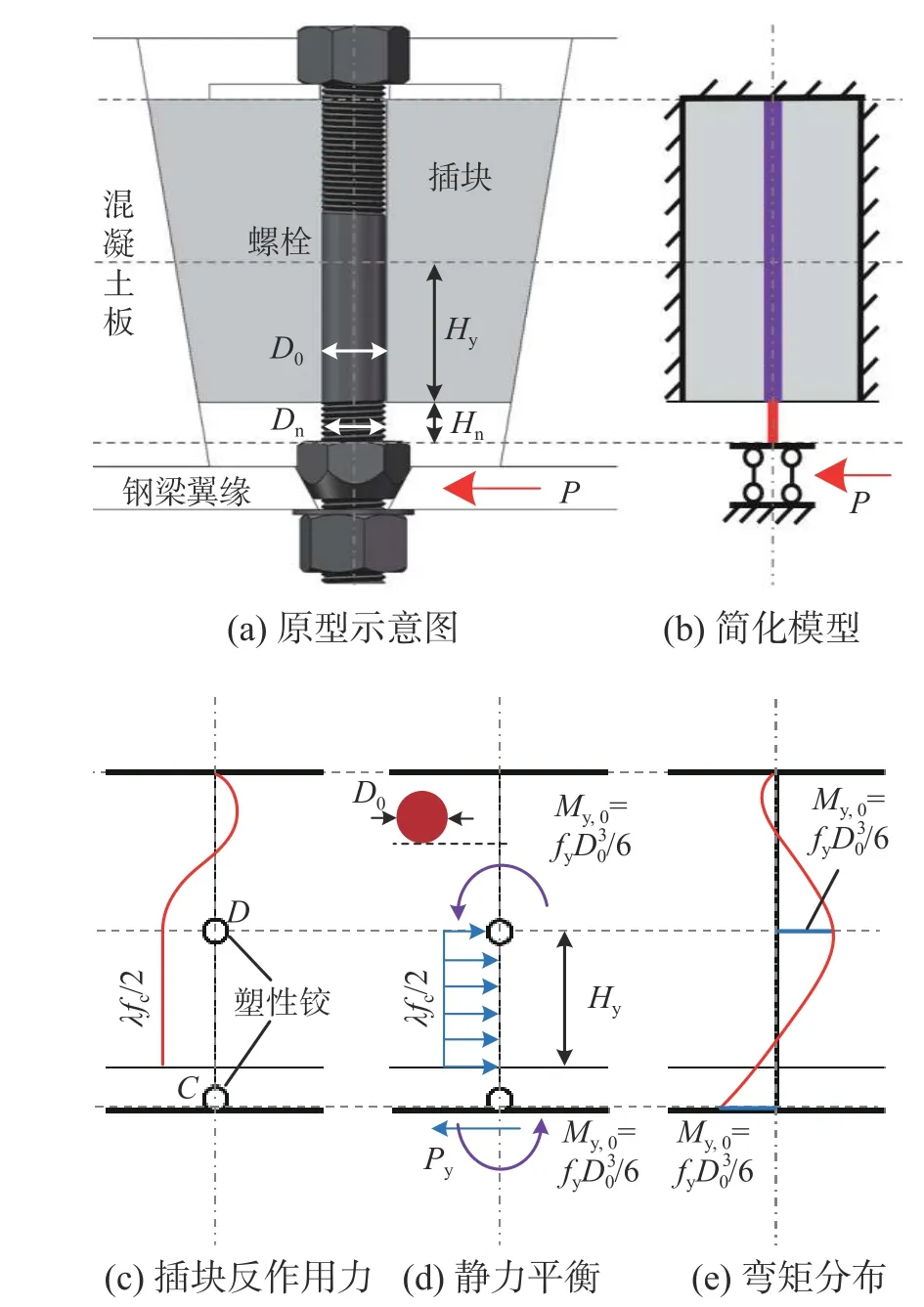
图6 PTBSC 屈服抗剪承载力力学机理Fig. 6 Mechanical mechanism of PTBSC yield strength

假设在两个塑性铰C和D之间混凝土的反力在整个区域达到侧向抗压强度，等效成大小为λfc/2(λ 为反力系数[26]，fc为插块的抗压强度)的均布荷载作用于该段螺栓，荷载分布如图6(d)所示。

因此，通过求解如图6(d)所示静力平衡，可得到PTBSC 如图6(e)所示弯矩分布图，以及屈服抗剪承载力Py理论计算公式。

根据图6(d)中静力平衡进行以下求解。

由水平方向的静力平衡∑FH=0，有：

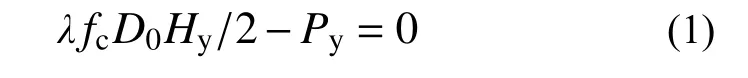
式中：λ 为反力系数，Broms 研究其范围在[8.28,12.56]，本文经过试算取与有限元分析结果最吻合的取值，取为λ=9；fc/MPa 为混凝土抗压强度；D0/mm 为螺栓光滑段直径；Hy/mm 为螺栓塑性铰D与插块下表面的距离；Py/N 为螺栓屈服时的剪切力。

由绕塑性铰C的弯矩平衡∑MC=0，有：

2.2 参数分析和公式验证

由于抗剪连接件的屈服抗剪承载力在工程设计中具有重要作用，本文对所提出的屈服抗剪承载力理论计算公式相关变量进行了如表1 所示参数分析，即螺栓直径D0、螺栓强度等级、集中变形段的长细比Hn/Dn、插块材料(混凝土)性能，以便为PTBSC 的工程应用提供设计参考。为减少分析参数，统一取Dn=0.88D0-1.17，该线性关系通过对工业标准手册中各型号高强螺栓的螺纹段有效直径与光滑段直径进行线性拟合得到。本节内容包含两方面：一是基于本文提出的屈服抗剪承载力的理论计算公式，探讨公式中的关键参数对其影响；二是以基于推出试验的有限元分析结果作为检验的对照样本，验证理论计算公式的有效性与准确性。

表1 研究参数范围Table 1 Range of parameters

1) 螺栓直径的影响

螺栓直径通常是影响抗剪连接件抗剪性能最重要参数，在所提出的屈服抗剪承载力理论公式中影响最为明显。图7 的曲线为屈服抗剪承载力随PTBSC 的螺栓直径变化的理论公式计算曲线(式(3))，随着螺栓直径的增加，PTBSC 屈服抗剪承载力不断增加，说明增加螺栓直径对PTBSC 的屈服抗剪承载力提高作用明显，但当螺栓直径小于10 mm，屈服抗剪承载力很小，因此在组合梁中不建议使用此直径范围值的螺栓作为抗剪连接件。

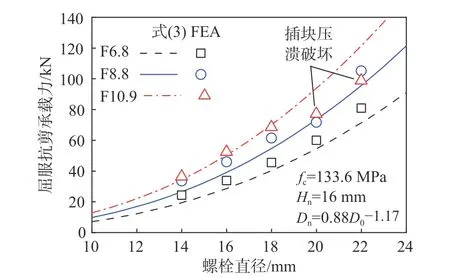
图7 螺栓直径对屈服抗剪承载力的影响规律Fig. 7 Effect of D0 on Py

图7 中的数据标记点为与理论公式相同的计算参数下的有限元分析结果。对比图7 中的理论公式计算曲线与有限元计算结果发现，理论公式计算结果与有限元计算结果吻合较好。只有在螺栓强度为10.9 级时，螺栓直径大于M20 时PTBSC发生插块压溃破坏，理论计算结果大于有限元分析结果，过高预测了屈服抗剪承载力Py。

2) 螺栓屈服强度的影响

螺栓屈服强度作为抗剪连接件材料性能的指标，也是其抗剪性能的重要影响参数。图8 的曲线为屈服抗剪承载力Py随PTBSC 的螺栓屈服强度变化的理论公式计算曲线，随着螺栓材料屈服强度fy的提高，PTBSC 屈服抗剪承载力理论公式计算值随之增大，增长的速率逐渐减小，说明螺栓屈服强度的提高，对PTBSC 屈服抗剪承载力的影响越来越小，由于实际工程抗剪性能需求，PTBSC中所使用的螺栓建议采用高强螺栓，即强度等级在6.8 级和12.9 级之间，强度等级不宜过大以避免材料浪费，与减轻螺栓对混凝土和钢梁的损伤。

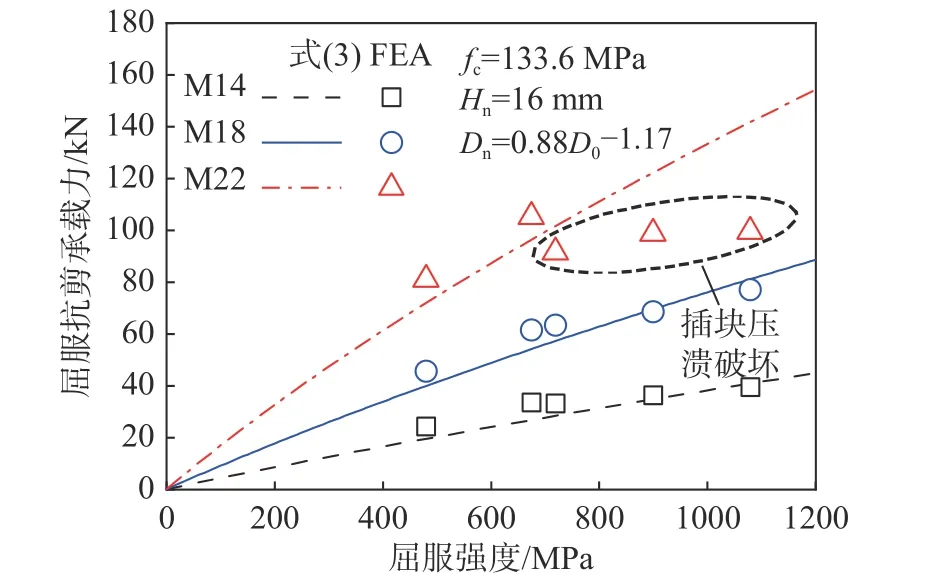
图8 螺栓屈服强度对屈服抗剪承载力的影响规律Fig. 8 Effect of fy on Py

当PTBSC 采用M14 和M18 时，理论公式的计算结果与有限元分析结果吻合得较好。当螺栓直径为M22 且螺栓强度等级大于8.8 级时，PTBSC发生插块压溃破坏，理论公式计算结果大于有限元分析结果，其原因是理论公式的计算假设前提为螺栓塑性屈服而插块不发生破坏。

3) 集中变形段长细比的影响

PTBSC 通过设置集中变形段来提高连接件的变形能力，集中变形段长度Hn的变化会影响连接件的抗剪性能。为使参数无量纲化，对Py和集中变形段的长细比Hn/Dn的关系进行研究。图9 中的曲线为屈服抗剪承载力随Hn/Dn变化的理论计算曲线，随着螺栓集中变形段长细比增大，PTBSC屈服抗剪承载力不断减小，当长细比大于2.5 时，Py基本没有变化，说明在设计中在满足PTBSC 变形要求的情况下宜减小长细比，以获得更大的Py。

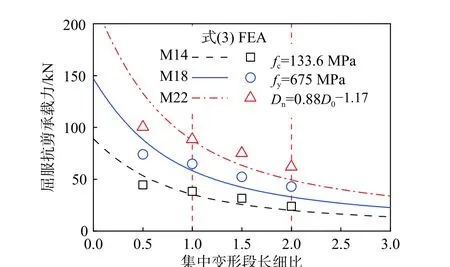
图9 集中变形段长细比对屈服抗剪承载力影响规律Fig. 9 Effect of Hn/Dn on Py

经有限元分析结果发现，图9 中当Hn/Dn为0.5 时，理论计算结果明显大于有限元分析结果，其原因是该长细比不满足理论计算的弯剪变形假设，因此应避免Hn/Dn小于0.5。当Hn/Dn在1.0～2.0 时，理论公式的计算结果与有限元分析结果吻合得较好。

4) 插块材料抗压强度的影响

在钢-混凝土组合构件中，抗剪连接件周围的混凝土材料的力学性能对连接件的抗剪性能影响显著[27]。为提高PTBSC 的抗剪性能，本文对插块材料进行参数分析。图10 的曲线为屈服抗剪承载力Py随插块抗压强度fc变化的理论公式计算曲线。观察曲线发现，当插块材料的抗压强度超过50 MPa 后，Py增长缓慢；当插块材料抗压强度超过100 MPa，Py变化很小。由于本文所设计的PTBSC 既定的插块材料为UHPC，并且UHPC 的抗压强度大于100 MPa，因此上述论证为本文预先选定的UHPC 插块材料提供理论依据。

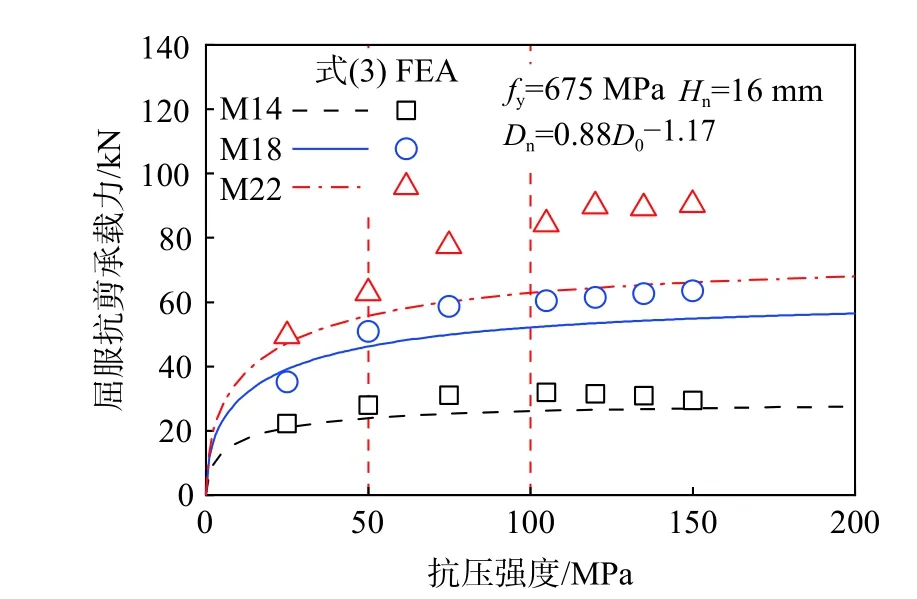
图10 插块材料抗压强度对屈服抗剪承载力的影响规律Fig. 10 Effect of fc on Py

5) 反力系数λ 取值的影响

为了比较反力系数的不同取值对式(3)的计算精度的影响，在已经确定反力系数的适当取值范围[8.28, 12.56]中选取4 个代表数值：8、9、10和12，并将其分别代入式(3)进行有效性和准确性验证。

将全部犯罪划分为轻罪和重罪，并通过简易程序，用较轻的刑罚方法制裁轻罪，是域外许多国家的普遍做法。在我国，关于建立轻罪制裁制度的建议也很早就有学者提出[1]，但由于我国的犯罪成立标准总体较高，犯罪圈较小，故这一建议一直未引起应有的重视。近年来，随着劳动教养制度的废止和《刑法》的第八、九次修正，大量原属治安违法或行政违法的行为被纳入犯罪圈，我国轻型犯罪的规模迅速扩大。在此背景下，构建轻罪制裁制度的呼声日益高涨。笔者也赞同这一提议。“通过程序繁简、刑罚轻重的不同安排，合理配置资源，以快速简易程序轻缓处罚治理大量轻微犯罪，而将有限资源集中处理少数严重犯罪，这是科学治理犯罪的基本要求。”[2]

图11 数据标记点为PTBSC 屈服抗剪承载力Py理论计算结果和有限元分析结果，对角实线为横纵轴等值线。图11(a)～图11(d)中理论计算公式中的反力系数λ 分别使用8、9、10 和12。经统计分析得出：与λ=9 相比，代入其他数值下理论计算结果与有限元分析结果的比值平均值的差值在正负0.03之内，对应的变异系数(coefficient of variation, CoV)差值在正负0.02 之内，说明λ 对Py影响很小，因此本文取反力系数λ=9 进行计算。

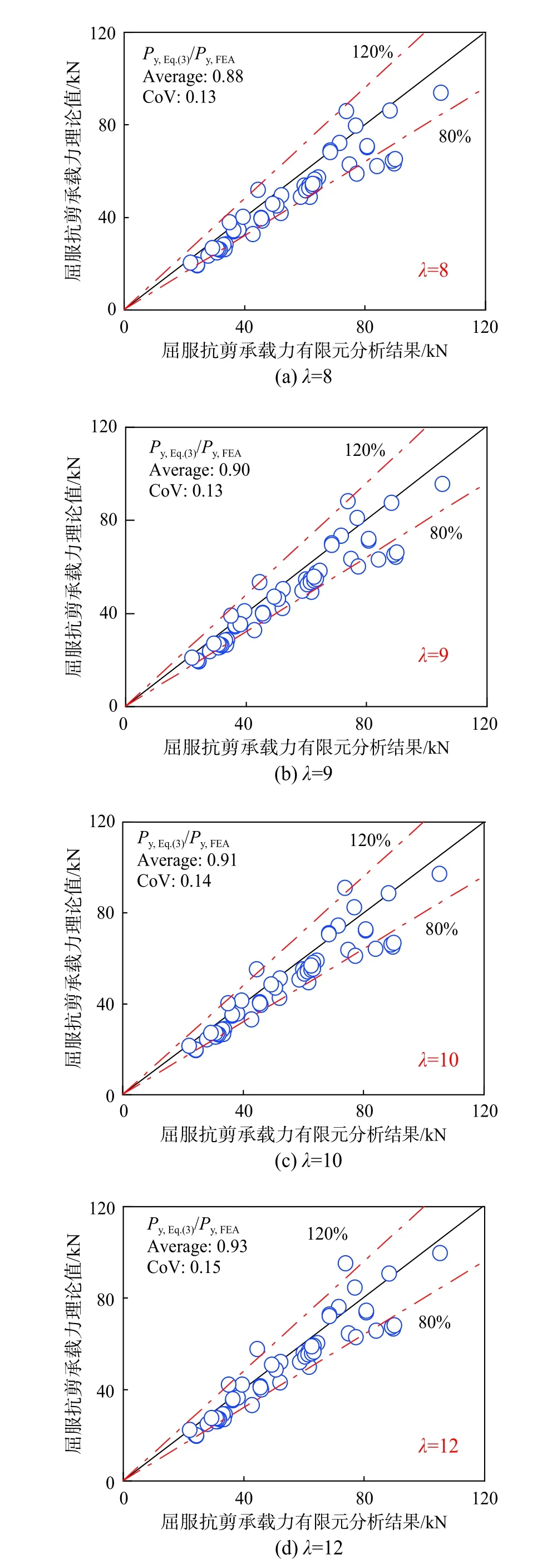
图11 屈服抗剪承载力理论公式和反力系数λ 评估Fig. 11 Evaluation of theoretical formula for Py and λ

Py标记点分布在等值线两侧，理论计算结果与有限元分析结果偏差在正负20%之内，吻合较好。因此，本文所提出的PTBSC 屈服抗剪承载力理论计算公式具有较好准确性，可用于指导PTBSC的工程设计和应用。

3 极限抗剪承载力的评估公式

极限抗剪承载力是PTBSC 的剪切-滑移关系曲线中的关键指标，需要对其进行定量评估。

目前，国内外针对抗剪连接件极限抗剪承载力的计算及预测，主要针对混凝土压溃破坏和连接件剪断破坏两种破坏模式分别提出相应的计算公式。本文所提出的PTBSC 构造措施使其只有螺栓集中变形段剪断破坏一种破坏模式，因此仅需对螺栓剪断破坏模式下的极限抗剪承载力进行理论评估。当螺栓抗剪连接件的破坏模式为螺栓剪断时，其极限抗剪承载能力一般表示为Pu=αAscfu。其中，不同的研究针对α 的取值有不同的建议，如Kwon 等[22]取α=0.5，Liu 等[23]取α=0.66。如图12 所示，本文提出的新型抗剪连接件极限抗剪承载力采用相同的表达式，α 的取值通过对有限元分析结果中的极限抗剪承载力进行统计回归分析来确定。

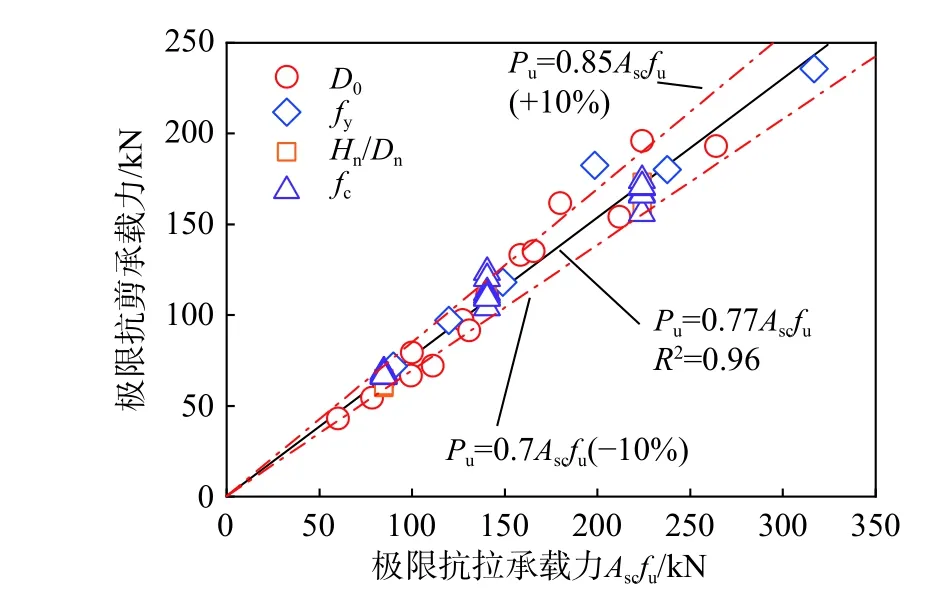
图12 PTBSC 极限抗剪承载力理论公式评估Fig. 12 Evaluation of theoretical formula for Pu of PTBSC

计算发现，有效的样本数据线性回归所得α=0.77，相关指数R2=0.96，具有较高准确性，因此可得出PTBSC 极限抗剪承载力回归公式Pu=0.77Ascfu。图12 中实线为回归线Pu=0.77Ascfu，图中各数据标记点分别为四种研究参数所得极限抗剪承载力，有限元分析结果与回归线偏差在正负10%之内，即系数α 在0.7～0.85 变化。本文为提出可用于指导PTBSC 的工程设计和应用且具有一定安全储备的Pu理论计算公式，取系数α 为下限值0.7，因此可得理论计算公式Pu=0.7Ascfu。

4 结论

本文为实现装配式钢-混凝土组合梁的可拆卸功能的目标及其抗剪连接件的变形能力改善需求，提出了一种高变形能力的插块式螺栓抗剪连接件。通过对新型高变形能力抗剪连接件的抗剪承载力进行受力分析，提出了相应的理论计算公式，得出主要结论如下：

(1) 根据PTBSC 推出试验和有限元分析研究发现，PTBSC 的剪切-滑移关系曲线存在明显的屈服点和极限点，曲线呈现出近似双线性特征。同时，曲线有较大的屈服后刚度(为初始刚度的1/3～1/2)，以及较大的屈服后承载力储备(极限承载力接近2 倍的屈服承载力)。

(2) 针对PTBSC 的屈服抗剪承载力和极限抗剪承载力，分别提出了相应的理论计算公式，经有限元分析验证表明，所提出的理论计算公式均有较高的精度。

(3) PTBSC 的屈服抗剪承载力随螺栓直径、螺栓屈服强度的增加而显著提高；随集中变形段长细比增大而变小，长细比在1.0～2.0 时，理论公式计算结果能较精确地预测PTBSC 的屈服抗剪承载力；当插块材料抗压强度超过100 MPa，屈服抗剪承载力提高的幅度变化很小，因此本文预先选定UHPC 插块材料经理论分析是合理的。