多角度观察 多维度思考 多手段处理——一道多元函数最值问题的求解

广东省惠州市第一中学 (516007) 钟时泉

多元函数最值问题是指含有多个变量、以求解最大值或最小值为目的的一类数学问题．多元函数最值问题中蕴含着丰富的数学思想和方法，而且有利于培养学生数学解题思维和能力.怎样求多元函数的最值，是师生们非常关注的问题，也是高中生必须具备的解题技能.本文借用一道多元函数最值问题的求解，通过一题多解及解法演变，以点带面，连点串线，不仅激发了学生的好奇心与求知欲，而且帮助学生拓宽解题思路，提高数学素养.

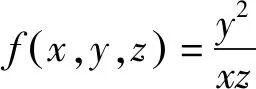
1.利用消元法求解

“消元法”是处理多元最值问题的一种常见方法，所谓消元法是指根据题设或题目所求结论，直接消去一个或多个变量，或者通过变形、构造把多个变量转化成一个变量的问题，把原问题变换角度进行研究.

2.巧用换元法求解

“换元法”也是处理多元最值问题的一种常见方法，所谓换元法是指根据题设或题目所求结论，引入一个或多个新“元”代换原来问题中的旧“元”，通过换元对原问题进行变换，使得问题变为简单，从而便于求解.

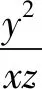
在解决多元最值问题中，三角换元是常客，由于本题没有常见的平方和等于1，那么该如何借用三角换元法去解决呢？

评注：换元的实质是转化，它是用一种变数形式取代另一种变数形式,关键是构造元和设元，理论依据是等量代换，目的是变换研究对象.

评注：题海茫茫，变化无穷，通常数学问题中已知与未知之间的联系并不明显,有时甚至好象隔着一条难以逾越的鸿沟，本题借用引进参数m，牵线搭桥,沟通了已知与未知的联系,可使问题迎刃而解．

3.借用构造法求解

“构造法”就是根据题设条件或结论所具有的特征、性质，构造出满足条件或结论的数学模型，借助于该数学模型解决数学问题的方法.

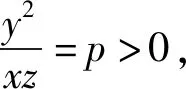
评注：从表面上看，本题纯属代数中的函数问题，但根据多元函数式及条件的结构特点，联想到与之相应的几何模型和代数背景，通过挖掘代数问题中蕴含的几何含义，使问题获得了简捷快速的解答．其解法独特，实属巧妙，体现了数学的奇异美.

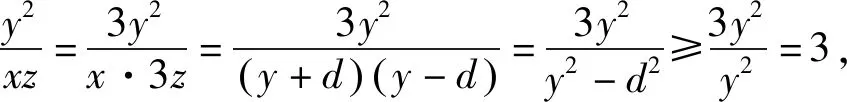
评注：由于2y=x+3z，看到这个等式很容易联想到等差中项，于是构造等差数列辅助求解，巧妙的构造给解题带来了意想不到的神奇效果.

评注：回顾解法3的整体换元，在求解过程中出现了y2=txz，由这个形式我们不难联想到等比中项,于是构造等比数列辅助求解.其解法新颖别致,独树一帜，可唤起学生的求知欲,诱发他们的好奇心,培养他们的创造力.

4.引用配凑法求解

“配凑法”是一种迂回的解题方法，体现了化归的思想，它指的是在解答数学问题的过程中，巧妙地配、凑一些适当的数、式或图形，以获得或化归成利于解答的形式.

综上,一题多解，殊途同归，是数学解题的一大奇观.一题多解对于提高学生的学习能力是十分必要的,但一题多解的最终目的不是用来展示有多少种解决问题的途径,也不是所有的题目都需要用多种方法求解.通过一题多解的教学，学生的数学思维可以得到锻炼，并且从不同的角度对问题进行深入思考，可提高学生的解题能力，达到一举多得的效果.研究表明，一题多解也是被认为是培养学生创造性思维的有效手段.