理解运算本质，破解不对称式

江苏省张家港市外国语学校 (215600) 何 威

一、问题提出

解析几何中的定点定值问题是常考的一类题型，韦达定理法是一种常见的方法，其过程一般为：将直线与圆锥曲线联立，由韦达定理得到关于x1,x2或y1,y2的一组对称的等式，再将题中所给的关键条件，转化韦达定理上，即可设而不求.但在实际计算中并不是总能如此顺利，如当目标式不对称式时，韦达定理使用遇阻，导致很多学生运算止步不前.

数学运算是新课标关注的核心能力，教学中特别要关注对运算本质的理解和对运算方向的预判.运算是一种演绎推理，包含着程序化思想.理解运算的问题，明确运算的方向，进而构造运算的程序，才能有效进行运算.以下以近期高三调研测试为例，谈一谈笔者的体会.

二、试题呈现

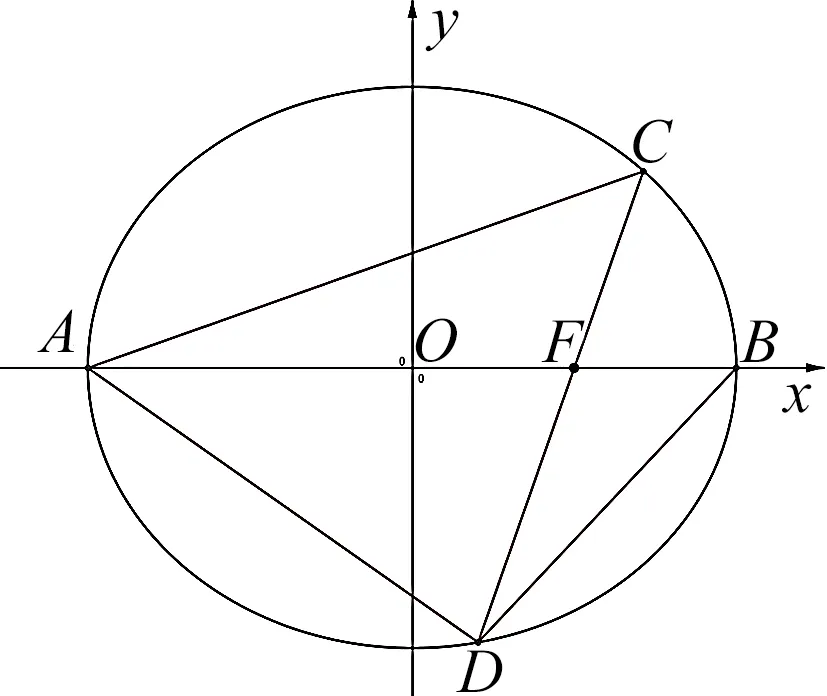
图1

三、消元法探析

韦达定理的本质是：通过设而不求，消减多变量，得到结构简单、少元的形式，从而整体运算得到定值.在韦达定理中，出现了三个元y1,y2,m，只有两个方程，本质上是方程的思想，消元才是核心，至于是否是消去y1,y2，则应视目标式情况而定.因此破除思维定势，关键在于确定留下哪些元，消去哪些元，请看如下不同视角的消元处理.

视角一：直接通过求根公式消元

评注：该解法直接借助求根公式消元，得到关于m的一元结构式，虽然看起来根式略显复杂，学生往往不敢算下去，其实代入后就柳暗花明.

视角二：利用韦达定理消m

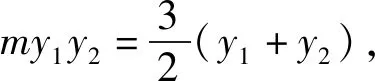
视角三：借助韦达定理消去y1

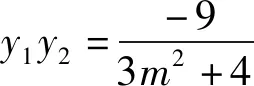
评注：视角三与视角二处理方法类似，实现整体消除.

视角四：利用椭圆方程消元

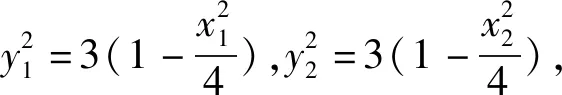
评注：前三种做法运用了实际上是借助直线方程x=my-1消去了x1,x2，而视角四先借助椭圆的方程，转化为对称式的结构，从而直接使用韦达定理消元.韦达定理式是直线与椭圆的方程联立得到的，学生在运算时常常知道利用直线的方程消参，却忽略了借助椭圆方程也可以消参，调整目标式的结构.

视角五：抓住椭圆中的斜率性质，转换目标式

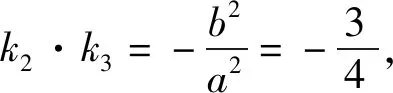
四、总结反思

综合以上解法，对于这类问题三元两等式的问题，处理目标式有三种策略：一是直接使用韦达定理，消去x1,x2(或y1,y2)，设而不求；二是转而消去其他的参数，留下一元或二元式，实现整体运算得到定值；三是运用已知条件或椭圆的性质，转化目标式，使目标式对称.这三种策略本质上都是抓住韦达定理中的变量关系，减少参数，使得目标式在消元后更加简洁、对称，从而更好地保持整体性，实现设而不求.

数学运算是解决数学问题的基本手段，反映了数学学科的基本特征，要求学生在“明晰运算对象的基础上，依据运算法则解决数学问题”.在本题中，学生算不对、算不下去，主要原因在于学生不能理解运算的意义和作用，未能形成合适的运算思路，远远不是加减乘除的问题.例如视角二中消m，首先需要学生能“看”出韦达定理式如何用y1,y2表示m；视角四借助椭圆方程处理目标式，需要理解运算的起点，未知量的来源；视角五需要熟悉“识”图合理联想，运用斜率结论简化运算，这些技巧中都蕴含了对运算对象的观察，对运算目标的转化，体现了运算是一种典型的逻辑推理，充满了辩证与选择.面对学生出现的运算错误，要作深入的分析，了解学生的想法，不能简单的归结为粗心，片面的追求运算速度.只有在深入理解运算对象和法则的基础上，形成好的思维品质，才能真正提高运算的质量与速度.