关于函数零点之差不等式问题的探究
2021-11-10重庆市长寿中学校401220
重庆市长寿中学校 (401220) 田 鹏
1 问题提出
如果一个函数有两个零点,这两个零点的差往往不能得到一个精确的值,尤其是在含参数的问题中,零点的差更难求出一个精确的值.因此,这类问题往往以不等式知识为载体,综合运用导数知识证明不等式问题.主要考查数形结合,转化与化归,分类与整合等数学思想.难度偏大,技巧性较强,抽象程度高,对直观想象,数学运算等数学素养要求较高.本文通过一些典型的例题说明这类问题的几种常见处理方法,以供读者参考.
2 数学模型
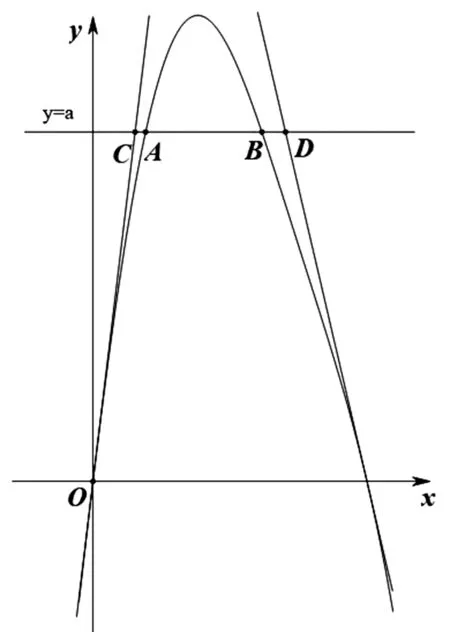
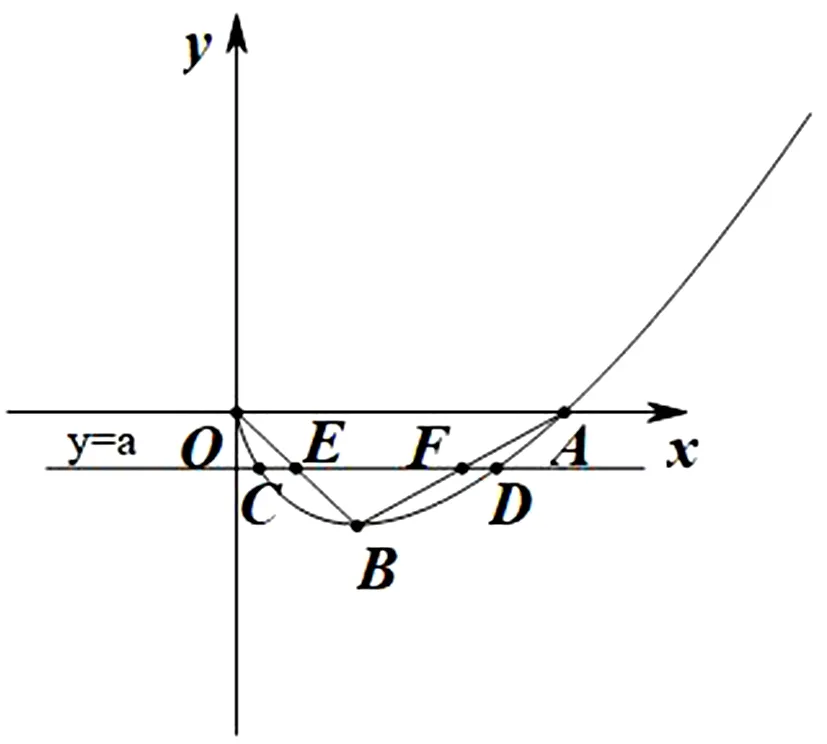
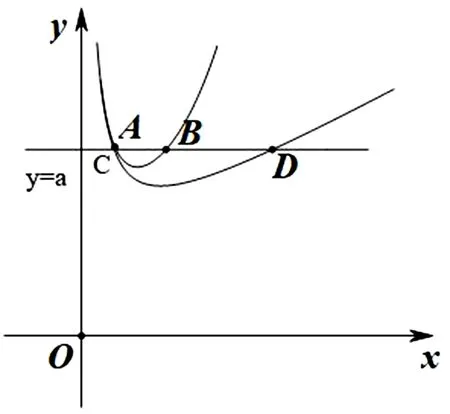
模型1 设函数y=f(x),y=g(x),若直线y=a与函数y=f(x)和y=g(x)分别交于点A(x1,y1),B(x2,y1),不妨设x1 模型2 设函数y=f(x),若函数的两个零点满足x1∈(a,b),x2∈(m,n),则m-b 图1 模型3 如图1,函数y=f(x)的图象下凹,直线AD,BD是函数y=f(x)的两条切线,且切线AD,BD恒在函数y=f(x)的图象上方,线段AC,BC是函数y=f(x)的两条割线段,且割线段AC,BC恒在函数y=f(x)的图象下方.直线y=a与切线AD,BD分别交于E,F两点,与y=f(x)的图象分别交于M,N,与割线段AC,BC分别交于G,H.设M(x1,y1),N(x2,y2),E(x3,y3),F(x4,y4),G(x5,y5),H(x6,y6),则x6-x5≤x2-x1≤x4-x3.该模型主要是通过切线放缩和割线放缩来解决,更一般地,可通过曲线进行放缩.若函数y=f(x)的图象上凹,也有类似的结论. 例1 设函数f(x)=2x+3-a,g(x)=ln(2x)-a的零点分别为x1,x2,则|x2-x1|的最小值为. 评注:结合零点的定义,可构建方程f(x1)=0和g(x2)=0,从中可解出x1和x2,进而构造函数,特别注意其中的参数a的范围.另外,若f(x1)=0或g(x2)=0不可解时,注意变量的选取,此时往往将x1和x2其中一个作为变量来构造函数. (1)设函数h(x)=(x-1)F(x),当a=2时,证明:当x>1时,h(x)>0; (2)若F(x)>0恒成立,求实数a的取值范围; 评注:此题难度较大,综合性强,思维灵活.主要考查利用导数来分析函数的图象与性质问题,利用零点存在定理来逼近函数的零点.其中将F(x)的零点转化为g(x)的零点这一步很关键,用零点存在定理可得x1∈(e-a,t1),x2∈(t2,ea),最后结合一元二次方程的韦达定理顺利得到证明.对这类问题,应深入分析不等式结构,通过直观想象,数据分析,找到问题的突破口,理清解题思路. 例3 已知函数f(x)=2sinx-x2+2πx-a. (1)当a=0时,求f(x)在其零点处的切线方程; 图2 解:(1)当a=0时,f(x)有两个零点x=0和x=2π.f(x)在x=0的切线方程为y=(2+2π)x;f(x)在x=2π的切线方程为y=(2-2π)(x-2π),过程略. 评注:函数f(x)的零点等价于函数g(x)=2sinx-x2+2πx的图象和直线y=a的交点,由(1)可得函数g(x)的两条切线.接着证明g(x)≤(2+2π)x和g(x)≤(2-2π)(x-2π)在定义域内恒成立,进而得到x2-x1≤x4-x3,而x3和x4可以解出来,问题得证.这类问题的关键是分析函数的图象特点(画出函数的大致草图),寻找函数的两条切线,至于寻找函数的切线没有通法可言,常用的经验是根据不等式的结构,大胆猜测,小心求证,方能顺利解决问题. 例4 已知函数f(x)=xlnx-a(a∈R). (1)讨论f(x)的零点个数; (2)若f(x)有两个不同的零点x1,x2,且x1 图3 (1)当a=1时,比较f(x)与x+1的大小; 解:(1)当a=1时,f(x)>x+1恒成立,过程略. 图4 函数问题内容多,方法多,技巧多,本文着重从函数的零点之差的视角进行探究,很可能本文中的这些例题还有其他的方法解决,这一点留给读者去探索.另外,在学习和研究这类问题时,要注意以下几点,其一,注重基础知识的积累,勤于思考,勤于探究,多积累解题经验,不断提高学生分析问题,解决问题的能力.其二,建构常见的函数放缩模型,努力钻研典型试题,深度挖掘其背景知识,不断提高学生发现问题和提出问题的能力.其三,加强学生逻辑推理、数学运算等数学素养的培育.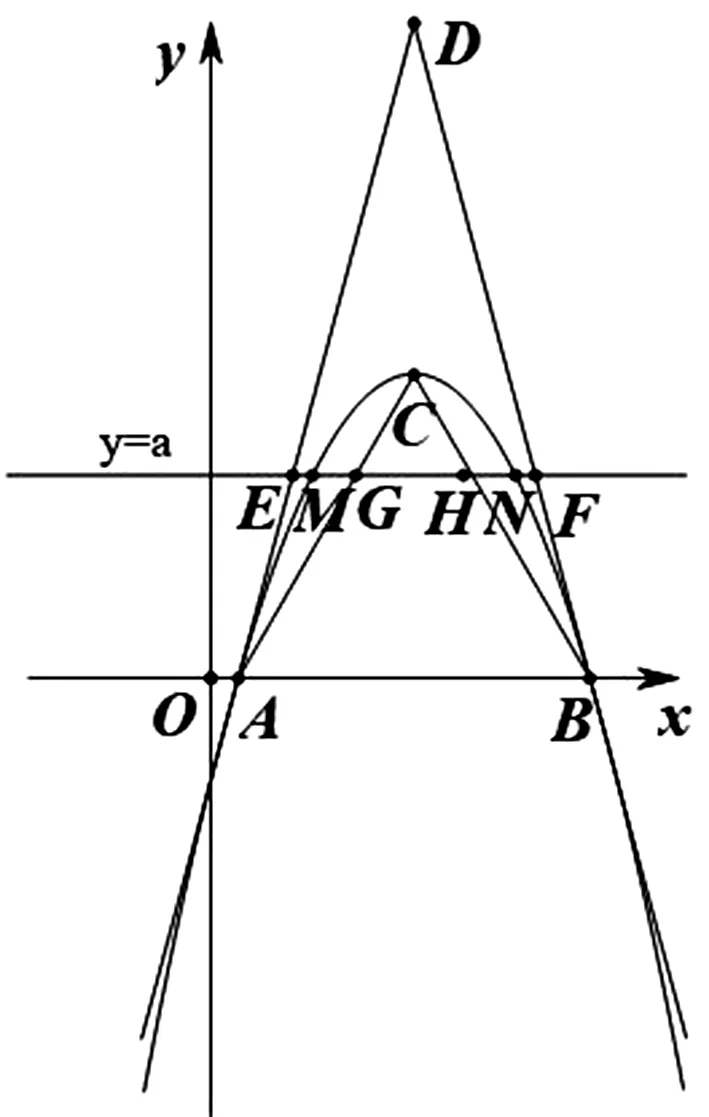
3 模型运用






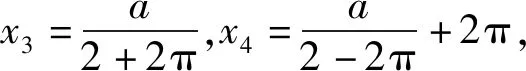


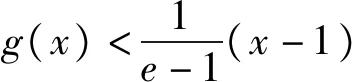



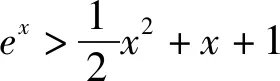
4 一点说明
