半结晶聚合物损伤演化的实验表征与数值模拟1)
2021-11-09薛世峰韩丽美刘建林
张 毅 薛世峰 韩丽美 周 博 刘建林 贾 朋
(中国石油大学(华东),山东青岛 266580)
引言
作为半结晶聚合物的一种,聚乙烯(polyethylene,PE)材料因其优良的物理和力学性能、耐腐蚀性以及便捷的安装和维护过程而被广泛用于制造排水和燃气管道.根据美国运输部管道和危险材料安全管理局的统计,2020 年美国新安装的燃气管道90%以上是由PE 材料制成的,产生了巨大的经济效益和社会效益,同时也面临着一系列严重的安全问题.由于材料缺陷、第三方损伤以及地壳运动等原因,PE 管道的失效破坏甚至爆炸等特大事故时有发生.因此对PE 材料力学性能以及损伤失效机理的研究对PE 管道的安全运行具有重要意义.
聚合物材料的力学行为与应力状态紧密相关.例如,很多聚合物材料单轴压缩屈服应力比单轴拉伸屈服应力要大.此外,有研究指出应力三轴度是控制韧性损伤起始最重要的因素[1].因此,自1976 年以来对不同应力状态的损伤断裂行为进行了一系列的研究,但主要是针对金属材料[2-15].通过改变预制缺口试样的缺口半径获得不同的应力三轴度水平,并且缺口半径越小应力三轴度越大.对缺口试样进行单轴拉伸实验得到的应力三轴度比较高,通常大于1/3.有学者通过对“蝴蝶状”试样进行单轴拉伸/剪切实验研究了材料在0~1/3 低应力三轴度状态下的力学行为[16-17].研究发现,金属材料的延展性和断裂应变随着应力三轴度的增大而逐渐降低.另一方面,考虑应力三轴度的损伤模型逐步发展完善,主要有两类,一类是连续介质损伤力学模型;另一类是基于多孔塑性理论的GTN 损伤模型.Bonora 等[18-20,13]基于Lemaitre[21]和Chaboche[22]提出的连续介质损伤力学框架发展了考虑应力三轴度的连续介质损伤模型.Brünig 等[6]通过有限元模拟和实验相结合的手段建立了考虑应力三轴度和洛德角的损伤准则.
近年来,对聚合物材料在不同应力状态下的损伤断裂行为的研究也取得了一定进展[23-33].对聚合物材料缺口圆棒试样的单轴拉伸实验结果表明:同等应变水平下聚合物材料的应力随着缺口半径的减小而增大[24-26,28-29,31,33],但断裂位移或断裂应变随着缺口半径的减小而减小[23-29].Ognedal 等[28]通过高速摄像机和扫描电子显微镜分别从宏观和微观角度研究了聚氯乙烯和高密度聚乙烯(high density polythylene,HDPE) 材料在三轴应力状态下的体积应变和孔洞变化规律,研究发现缺口半径越小体积应变越大、孔洞数量越多.此外,也有研究通过有限元模拟和实验相结合分析聚合物材料试样横截面上应力三轴度的分布[26,28]和孔隙度的分布[26-27].由此可见,文献中对聚合物材料不同应力状态下损伤行为的研究以定性分析为主,未能定量描述聚合物材料在不同应力状态下的损伤演化过程.
因此,本文提出一种可以定量表征聚合物材料损伤演化的两阶段实验测试方法,结合微观结构演化分析系统地研究了应力状态对聚合物材料损伤演化的影响;提出了适用于聚合物材料的损伤模型参数确定方法,并将得到的损伤模型用于PE 材料冲压实验的有限元模拟,模拟结果与实验结果吻合良好,证明了其可行性和适用性.
1 实验分析
1.1 实验材料
实验材料为HDPE,其重均相对分子质量和密度分别为63 069 g/mol 和0.940 g/cm3.为得到不同应力状态下的损伤演化方程和断裂应变,设计了4 种不同尺寸的缺口圆棒试样,其缺口半径分别为0.5,2,5 和20 mm,具体试样尺寸如图1 所示.4 种试样均由直径为10 mm 的HDPE 圆棒加工得来,并且圆棒最小直径均为6 mm.所有实验都通过电子万能试验机完成,并采用径向电子引伸计测量变形过程中试样中间位置(即横截面积最小处)的直径变化(如图1 中小图所示).

图1 缺口半径为20,5,2 和0.5 mm 的圆棒试样Fig.1 Example Axisymmetric specimens with notch radii of 20,5,2 and 0.5 mm
1.2 实验流程
单轴拉伸实验:以1 mm/min 的恒定速度对4 种缺口圆棒试样进行单轴拉伸实验直至试样断裂,并采用扫描电子显微镜分析断口形貌.
两阶段实验:为定量描述HDPE 材料的损伤演化过程,本文采用两阶段实验法对缺口圆棒试样进行损伤表征.第一阶段实验为损伤引入,其实验流程如图2 所示,首先以1 mm/min 的速度将圆棒试样拉伸至不同的位移(加载阶段),紧接着保持位移不变10 000 s (应力松弛阶段),最后以0.1 mm/min 的速度卸载(卸载阶段).将卸载后的试样放在干燥、避光的环境保存2 个月.第二阶段实验为损伤表征,即将第一阶段拉伸过的试样以0.01 mm/min 的速度再次进行单轴拉伸实验直至试样断裂.
中断实验:将采用图2 实验流程拉伸到不同位移后卸载的R2 和R20 试样放入液氮中脆断,应用扫描电子显微镜分析试样在变形过程中的微观结构演化规律.

图2 第一阶段实验流程示意图Fig.2 Schematic description of the test procedure used in the first stage tests
冲压实验:采用如图3 所示的冲压实验装置对40 mm×40 mm×3 mm 的HDPE 平板进行冲压实验.压头直径分别为4,6,8 和10 mm,冲压速度为1 mm/min,并记录冲压过程的载荷-位移曲线.

图3 HDPE 冲压实验有限元模型Fig.3 Finite element model for punch test on HDPE
2 有限元分析
2.1 有限元模型
缺口圆棒试样有限元模型:对4 种缺口圆棒试样的单轴拉伸实验进行有限元模拟,以获取4 种缺口圆棒试样对应的应力三轴度.该部分工作在文献[34]中有详细介绍,此处不再赘述.
冲压实验有限元模型:为验证本文提出损伤模型的正确性,对HDPE 平板的冲压实验进行有限元模拟分析.考虑到试样、压头和压杯均为轴对称结构,为减小计算量,建立如图3 所示轴对称模型.HDPE平板采用CAX8R 单元,压头和压杯采用刚体进行分析并设立参考点.模拟过程中,固定压杯,压头以一定速度向下移动,提取压头参考点的作用力和位移,并与实验结果对比分析.
2.2 有限元本构方程
Kwon 和Jar[35]提出的四段式唯象学本构模型成功用于PE 材料的大变形及断裂行为的描述.因此,本文采用上述本构模型进行有限元分析,具体方程为

式中,σeq和ε 分别为等效应力和等效应变,εy为线弹性段到非线弹性段的转折应变点,εn为颈缩起始应变点,εt为应变硬化起始应变点.其他参数,包括a,b,c,d,e,αk,k,N,M,β 为用户自定义参数.本文通过迭代程序调整上述参数直至模拟结果与实验结果吻合.方程(1a)为胡克方程,用于描述HDPE 材料线弹性力学行为[36-37];方程(1b)为修正Ogden 方程[38],用于描述HDPE 材料非线弹性段的力学行为;方程(1c)和(1d)为Hutchinson 和Neale[39]提出的描述应变硬化行为的应力-应变方程.
3 非线性损伤模型
连续介质损伤力学采用损伤变量D从宏观层面描述材料的损伤演化过程.损伤变量定义为参考体积单元中存在的不可逆缺陷(微孔洞、微裂纹等)的比率,例如D=0 表示无损伤的完整材料.连续介质损伤力学的假设是当损伤变量达到临界值Dcr时,材料失去承载能力[40-41],宏观裂纹和失效破坏产生.损伤会引起弹性模量等力学性能的衰退,在应变等效假设下,损伤变量可以采用下式计算

式中,ED和E0分别表示有损伤和无损伤材料的弹性模量.
Borona 等[18]提出金属材料韧性损伤演化过程中的损伤耗散能

式中,Dcr表示宏观裂纹产生时的临界损伤变量,S0是材料参数,n是Ramberg-Osgood 材料硬化指数,α是决定损伤演化曲线形状的损伤指数,p为累积等效塑性应变.Y表示应变能释放率

式中,σeq表示等效应力,f(η) 是应力三轴度η(η=σH/σeq,其中σH和σeq分别为静水压力与等效应力)的方程,其表达式为
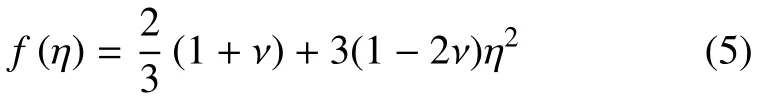
式中,ν 为泊松比.
将式(3) 中的损伤耗散能对应变能释放率求导数可得

将式(4)代入式(6)可得

根据Ramberg-Osgood 幂法则[39],等效Mises 应力可以描述为累计塑性应变的函数
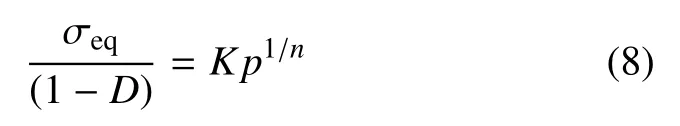
损伤演化的动力学规律可以描述为[5]

将式(7)和式(8)代入式(9)可得


将式(11)代入式(10)可得

对式(12)进行积分可得

在单轴加载情况下,材料破坏失效时的累计塑性应变pf等于材料单轴拉伸失效时的塑性应变εf;材料损伤起始时的累计塑性应变pth等于材料单轴拉伸损伤起始时的塑性应变εth.因此,式(13) 可以改写为

式(14)中的损伤模型将会用于HDPE 材料不同应力状态下损伤演化的定量描述.该损伤模型需要确定5个材料参数,分别为无损伤材料的初始损伤变量D0,宏观裂纹产生时的临界损伤变量Dcr及其对应的断裂应变值,损伤开始时对应的临界应变值εth和损伤指数α.
4 结果和讨论
4.1 应力三轴度对损伤演化的影响
对4 种缺口半径的HDPE 圆棒试样进行单轴拉伸实验,基于公式[42]

式中,σEng为工程应力,σT为真应力,εT为真应变.A0和A分别为试样变形前和变形过程的横截面面积,通过夹持式径向电子引伸计测得的直径计算得来.引伸计夹具与试样接触处设计为楔形,方便固定到R0.5 和R2 圆棒式样的缺口中.对拉伸试样的数据进行处理,可得HDPE 材料的工程应力-位移和真应力-真应变曲线(如图4 所示).由于所选用的HDPE 材料的应力-应变曲线重复性很好,故图4 中针对各缺口半径只列出一个试样得到的应力-位移和应力-应变曲线.由图4 可知,R20 试样的工程应力-位移曲线可以分为4 个阶段,分别为弹性阶段、屈服阶段、颈缩阶段和应变硬化阶段.但是随着曲率半径的逐渐减小,最后的应变硬化阶段逐渐弱化直至完全消失.此外,HDPE 的屈服应力随着曲率半径的减小而增大,但断裂位移或断裂应变随着曲率半径的减小而减小,这与文献[23-29]中的结果是一致的.由图4(a)试样拉伸断裂后的图片也可看出,随着曲率半径减小,HDPE 试样由韧性断裂转变为脆性断裂.图4(b)的结果表明,在真应变相同的情况下,缺口半径更小的HDPE 试样表现出更高的应力水平.

图4 缺口圆棒试样的单轴拉伸实验结果Fig.4 Experimental results from uniaxial tensile tests on notched round bar specimens
HDPE 缺口圆棒试样单轴拉伸断裂后的形貌分析表明曲率半径较大的HDPE 试样断裂表面有明显的韧性延展,并伴有纤维化现象,如图5(a)和图5(b)所示.作为半结晶聚合物,HDPE 由结晶区-非晶区-结晶区三明治分子结构组成.在拉伸变形过程中,相邻结晶区发生相对错动的剪切变形、结晶区自身发生旋转运动以及结晶区内分子链的解缠绕会导致分子链逐渐沿着拉伸方向取向.HDPE 材料的这种局部取向包括结晶区和非晶区分子链的局部断裂、重组、取向等过程,随着纤维的进一步拉伸,最终导致试样的韧性断裂.分子链局部取向引起的纤维化现象,宏观表现为图4 所示的应变硬化现象.因纤维化现象的存在,R20 和R5 的HDPE 试样断裂表面比较光滑,孔洞现象不明显.但是图5(c)和图5(d)所示的R2 和R0.5 试样断裂形貌表明曲率半径较小的HDPE 试样孔洞化现象更加明显,具体表现为孔洞数量增多、体积增大.

图5 缺口圆棒试样单轴拉伸断口形貌Fig.5 Tensile fracture morphology of notched round bar specimen
图6 为第一阶段实验测得的工程应力-位移曲线.按照图2 所示的实验流程将不同缺口半径的HDPE 试样拉伸到不同的位移,保持位移不变10 000 s 后以恒定速度卸载试样.需要说明的是,图6(a)~图6(c) 中将R20,R5 和R2 试样拉伸到6个不同位移后卸载,图6(d)对应的R0.5 试样只采用了5 个不同位移.这是因为R0.5 试样断裂位移比较小,故R0.5 试样只测试5 个不同位移.
为研究应力状态对HDPE 材料微观结构演化的影响,将R2 和R20 试样拉伸到图6 所示的位移并卸载后,放入液氮中脆断,而后采用扫描电子显微镜研究断裂表面的形貌,如图7 和图8 所示.图7(a)为将R2 试样拉伸到1.5 mm(屈服点之前)的断裂形貌,结果表明HDPE 材料屈服之前的微观结构变化比较微小,变形主要集中于比较软的非晶区.但是过了屈服点之后,HDPE 试样中出现了明显的孔洞并且随着变形的增大孔洞逐渐增大(图7(b)~图7(e)).孔洞附近伴随有不同程度的微裂纹,或银纹现象.

图6 第一阶段实验中拉伸到不同位移的缺口圆棒试样工程应力-位移曲线Fig.6 Curves of engineering stress versus displacement for notched round bar specimens with different radii stretched to various displacements in the first stage tests

图7 单轴拉伸下R2 试样的微观结构演化Fig.7 Microstructure evolution of R2 specimens subjected to uniaxial tension

图7 单轴拉伸下R2 试样的微观结构演化(续)Fig.7 Microstructure evolution of R2 specimens subjected to uniaxial tension(continued)

图8 单轴拉伸下R20 试样的微观结构演化Fig.8 Microstructure evolution of R20 specimens subjected to uniaxial tension

图8 单轴拉伸下R20 试样的微观结构演化(续)Fig.8 Microstructure evolution of R20 specimens subjected to uniaxial tension(continued)
图8 所示的R20 试样的微观结构演化.图8(a)为将R20 试样拉伸到2 mm (屈服点) 的断裂形貌,结果表明R20 试样在屈服点附近出现孔洞,这与文献[40] 中的实验结果是一致的.随着变形的增大,孔洞逐渐增大、融合(图8(b)和图8(c)).相比于R2试样,R20 试样产生明显的纤维化现象(图8(d)和图8(e)),宏观表现为图6(a)的应变硬化现象.
将第二阶段实验测得的HDPE 试样的弹性模量和屈服应力与未进行第一阶段拉伸变形的HDPE 试样的弹性模量和屈服应力进行比较,得到归一化的弹性模量和屈服应力随第一阶段实验拉伸位移(预应变)的变化规律,如图9 所示.结果表明HDPE 材料的弹性模量和屈服应力随着预应变的增大而衰减,而且试样缺口半径越小衰减程度越严重.这说明第一阶段实验对HDPE 材料的拉伸变形造成分子链的局部损伤,宏观表现为力学性能的衰退.根据式(2)和弹性模量的衰减可以计算得到不同缺口半径试样的损伤演化规律,如图10 所示.结果表明缺口半径越小,HDPE 材料的损伤萌生越早、演化越快.

图9 第一阶段实验中引入HDPE 试样的预应变对第二阶段实验测得的力学性能的影响Fig.9 Example effects of prestrain introduced in the first stage tests on mechanical properties of HDPE measured from the second tests
4.2 损伤模型参数的确定
式(14) 的损伤模型需要确定5 个参数,根据文献[19] 中对初始损伤变量的定义,这里取初始损伤变量D0=0,损伤演化指数α=1.其次采用D=A[1-exp(-Bε)]对图10 中实验测得的损伤变量进行拟合.采用拟合得到的曲线可以预测损伤起始时对应的应变值εth,以及单轴拉伸实验测得的断裂应变(图4(b)) 对应的临界损伤变量Dcr.采用式(1)本构关系和式(14)损伤模型对4 种缺口圆棒试样的单轴拉伸断裂进行模拟,获得每种试样对应的应力三轴度和损伤模型参数如表1 所示.图11 为采用式(14) 损伤模型预测得到的损伤演化与实验测得结果的对比,结果表明损伤模型可以比较好地描述HDPE 材料不同应力状态的损伤演化行为.

图10 损伤变量随第一阶段试验施加的预应变的变化规律Fig.10 Variation of damage parameter as a function of prestrain applied in the first stage tests

表1 损伤演化模型各参数的取值Table 1 Values of parameters in damage evolution model

图11 采用两阶段实验法测得的损伤演化与式(14)损伤模型对比Fig.11 Comparison of damage evolution determined from two-stage tests and predicted using model described in Eq.(14)
4.3 模拟结果与冲压实验结果对比
采用式(1)本构方程及表2 和表3 的本构方程参数和式(14)损伤演化模型及表1 的损伤模型参数对压头直径为4,6,8 和10 mm 的HDPE 平板冲压实验进行模拟,结果如图12 所示.本文提出的本构损伤模型可以较好地描述HDPE 平板冲压过程中的变形与损伤断裂行为,且冲压最大载荷和断裂位移随着压头直径的增大而增大.这是由于试样变形初期以弯曲变形为主,压头直径越大,载荷距边界约束条件越近,使试样发生弯曲变形的载荷越大.同时,不同压头直径对试样最终的断裂形式具有显著影响(如图13),随着压头直径的增大,试样断裂处的厚度减薄逐渐被“颈缩”现象所代替.这意味着随着压头直径的增大,试样的断裂模式由脆性断裂逐渐转变为韧性断裂,与图12 实验测得的结果相吻合.


图12 有限元模拟结果与冲压实验结果对比(续)Fig.12 Comparison of the FE simulation results with punch test results(continued)

图13 不同压头直径冲压下HDPE 平板变形Fig.13 Deformation of HDPE plate under punch test with various indenter diameters

表2 式(1)本构方程参数的取值Table 2 Values of parameters of constitutive equations described in Eq.(1)

表3 式(1)本构方程应变区间的取值Table 3 Strain ranges of constitutive equations described in Eq.(1)
5 结论
本文采用实验和有限元模拟对HDPE 材料在不同应力状态下的损伤演化的断裂行为进行了系统研究,提出了一种适用于聚合物材料的本构关系和损伤演化模型参数的确定方法.
(1)完成4 种缺口圆棒试样的单轴拉伸实验,获得了载荷-位移曲线和真应力-真应变曲线,结果表明载荷和应力随着试样缺口半径的减小而增大,但断裂应变随着缺口半径的减小而减小.
(2)基于缺口圆棒试样拉伸实验获得的载荷-位移曲线,采用实验和有限元模拟相结合的方法得到HDPE 材料不同应力状态的本构关系,并获得了4 种缺口圆棒试样对应的应力三轴度,结果表明缺口半径越小的试样应力三轴度越大.
(3)通过两阶段实验法测得了HDPE 材料不同应力状态下损伤变量与预应变的关系,结合单轴拉伸实验测得的断裂应变确定了非线性损伤演化模型中的参数,建立了HDPE 材料不同应力状态的损伤演化模型.
(4) 结合中断实验和扫描电子显微镜分析了HDPE 材料不同应力状态下的微观结构演化,结果表明高应力三轴度试样中的孔洞数量更多、体积更大,但取向纤维分子结构没有低应力三轴度试样多,宏观表现为高应力三轴度试样基本没有应变硬化阶段,且最终为脆性断裂.
(5) 基于HDPE 材料的本构关系和损伤演化模型,实现了对HDPE 平板冲压过程的精确模拟,模拟结果与实验结果有较好的一致性,表明本文提出的确定HDPE 材料本构关系和损伤模型的方法具有真实性和普适性.
