颗粒群碰撞搜索及CFD-DEM 耦合分域求解的推进算法研究1)

刘巨保 王 明,2) 王雪飞 姚利明 杨 明,3) 岳欠杯

*(东北石油大学机械科学与工程学院,黑龙江大庆 163318)

†(新加坡南洋理工大学机械与航天工程学院,新加坡 639798)

引言

在自然界和工业领域,流体中的颗粒碰撞普遍存在[1].如泥沙流中的砂粒碰撞与沉积[2],石油开采携砂压裂液中的颗粒碰撞与管壁冲蚀等.这些颗粒群与流体运移的两相流动中,流体输运的湍流效应和颗粒运动的碰撞相互影响[3].在颗粒体积分数低至4.0×10-4情况下[4],颗粒间的碰撞效应也不应被忽略.通常采用数值模拟手段来量化整个流场以及单个颗粒的动力学[5].

固液两相流动中,颗粒间接触和碰撞十分剧烈、复杂[6],成为影响两相流动行为的关键因素[7],也是数值模拟研究的热点和难点.固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8-9]和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10]两大类.前者将颗粒与流体视为互相渗透的拟流体或拟连续介质,在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性,适合进行大规模的工程问题计算,但忽略了颗粒离散特性,对颗粒流动行为的预测会与实际过程产生偏差[11],无法得到颗粒的运动轨迹[12].后者采用欧拉-拉格朗日坐标系研究两相流动,即流体作为连续介质,在欧拉坐标系研究,颗粒作为离散相,在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程,跟踪颗粒在流场中的复杂运动.欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度,取决于能否准确地刻画颗粒间的碰撞,而颗粒碰撞搜索算法成为解决这一难题的关键.

前人对颗粒碰撞搜索算法进行了大量研究,如分割单元算法也称网格单元算法[13-15],将计算域划分成均匀的立方体单元,单元长度为颗粒直径的整数倍.计算时间步结束时刻根据颗粒当前位置被分配到某个单元,只有同一单元或相邻单元内颗粒可能发生碰撞.一个颗粒最多占据8 个单元,当其成为目标颗粒时,只对其占据的单元内其他颗粒进行碰撞检测.该算法遗漏了那些时间步结束前,离开或穿过立方体单元,可能与目标颗粒发生碰撞的颗粒.Allen等[16]提出的邻居列表算法,规定了一个阈值距离来确定颗粒间相互作用的影响半径.碰撞搜索只对列表内的颗粒对进行搜索,如果两个颗粒之间的距离大于阈值距离,其就不可能在下一个时间步中发生碰撞.所以,邻居列表需要几个时间步更新一次.该算法构建的搜索列表内颗粒众多,在高浓度颗粒存在的应用中,每对颗粒进行一次判定计算代价过高.Vemuri 等[17]提出的八叉树算法,建立一个能够容纳任意方向上最大颗粒的立方体,将其作为划分域的基本单元.在对小颗粒进行搜索碰撞时,基本单元将会被多次划分八叉树,每个颗粒根据其大小与单元的关系,配置到对应单元中.在计算域内有多种尺寸颗粒时,需多次划分基本单元,计算过程繁琐.

Baraff[14]提出了边界盒算法,使用轴向对齐的边界盒来确定颗粒之间的碰撞.如果两个颗粒相撞,其在x,y和z维度上的正交投影将会重叠.3 个列表包含对轴的投影坐标,每个维度对应一个列表.在下一个时间步骤,需要再次对之前排序的列表进行排序.Li 等[18]提出的时间相干碰撞搜索算法(SMB),是将包围盒AABB 投影在笛卡尔坐标轴上,根据投影间距递增排序建立初步碰撞搜索列表,通过对列表内所有间距搜索检查确定是否重叠,建立碰撞列表.该算法适用于大量移动AABB 的系统,并支持对象的动态插入和删除,不受物体大小的限制.

上面几种方法对颗粒碰撞的判定,都采用较小的时间步长进行推进计算,根据计算时间步结束时颗粒位置,判断颗粒是否与目标颗粒碰撞.若时间步选取过大,会遗漏计算时间步内的颗粒碰撞效应[19],无法对颗粒碰撞导致的颗粒位置、速度、加速度等变化进行描述影响计算精度.而无限缩小颗粒计算时间步,又会造成推进次数的增加,影响计算效率.

此外,由于颗粒碰撞搜索方式的改变,颗粒与流体耦合方式也相应发生变化.传统CFD-DEM 耦合方法,流体计算时间步长是颗粒计算时间步长的整数倍(Δtf=n·Δtp)[20].流体完成一个时间步Δtf,颗粒完成n个时间步Δtp,颗粒与流体才进行一次相间力的交换,导致颗粒在流体内部受力及运动与实际误差较大.

针对CFD-DEM 耦合计算时,颗粒碰撞搜索时间步选取过小导致计算效率低、选取过大导致碰撞颗粒漏判的问题.本工作通过对颗粒碰撞搜索算法的研究,使颗粒计算时间步的选取尽可能大、且不受颗粒碰撞时间限制;依据颗粒与流体耦合条件,自适应调整流体计算时间步长,实时更新相间力.以期为颗粒-流体耦合计算提供一种高计算精度、高计算效率的计算方法.

1 流体与颗粒群耦合的数值分析方法

取管道内流体与颗粒群为研究对象,建立圆管内流体与颗粒群耦合的两相流模型,如图1 所示.该模型共分2 个域,颗粒群域Ωp和流体域Ωf.流体域入口采用速度边界Γin,出口采用压力边界Γout,速度和压力用uΓin,f和pΓout,f表示.管道内壁面边界(流体域与管道域耦合界面)Γint假定为无滑移,用uΓI,f=0表示.在圆管内两相流体系中任取一控制体dVc,该控制体内流体和颗粒占据的体积分别为dVf和dVp.

图1 流体与颗粒群耦合模型示意图Fig.1 Schematic diagram of fluid and particle group coupling model

1.1 流体控制方程

流体质量守恒方程为[21]

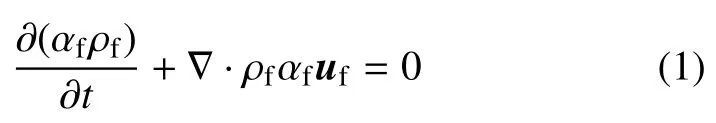
流体动量守恒方程为

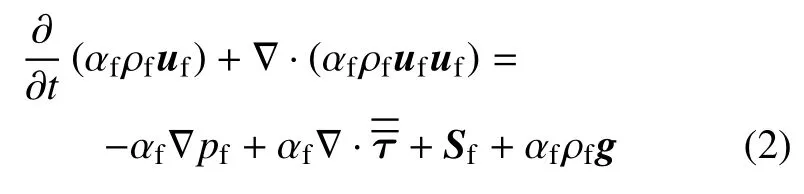
式中,ρf为流体密度,uf为流体速度矢量,pf为流体压力,g为重力加速度,αf为流体的体积分数;为流体黏性应力张量,Sf为流体与颗粒动量交换力源项.

两相流与单相流的主要区别在于,流体相中流体体积分数αf和源项Sf的变化.流体体积分数αf是流体单元中流体所占有的体积份额[22],Sf是颗粒与流体间动量交换力源项[23],如图2 所示.

图2 两相流体计算单元示意图Fig.2 Schematic diagram of two-phase fluid calculation unit

式中,VE为流体单元体积,αp为流体单元内颗粒占有的体积分数,为流体单元内第i个颗粒体积,为流体单元内第i个颗粒受到流体作用力,np为流体单元内颗粒个数;FE和ME分别为流体单元内所有颗粒与流体作用力的合力和合力矩,H为颗粒到流体单元质心的距离.

1.2 颗粒受力分析及动力学方程

1.2.1 颗粒与流体作用力分析

颗粒被裹挟在流体内部,跟随流体运动,不稳定的流态会对颗粒产生多种作用力,其合力Ff可表示为

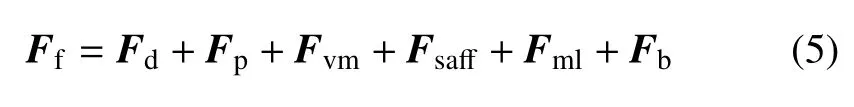
式中,Fd为颗粒在流体中受到的阻力(曳力),Fp为压力梯度力,Fvm为虚拟质量力[24],Fsaff为Saffman 剪切升力[25],Fml为Magnus 旋转升力[26],Fb为倍瑟特力[27].

由于颗粒直径较小,忽略Saffman 剪切升力、Magnus 旋转升力、压力梯度力、虚拟质量力、倍瑟特力对颗粒的影响[28].阻力(曳力)在流体作用于颗粒上的力中起主要作用[29].当颗粒的运动速度大于流体的流速时,流体作用在颗粒上的力表现为阻力,当流体的流速大于颗粒速度时,作用在颗粒上的力表现为曳力.计算公式为[30]

式中,Cd为曳力系数,Rep为颗粒雷诺数,Dp为颗粒直径,μf为流体表观黏度.

1.2.2 颗粒动力学方程

取任一颗粒i为研究对象,其运动由平移和旋转组成,根据牛顿第二定律得[31]

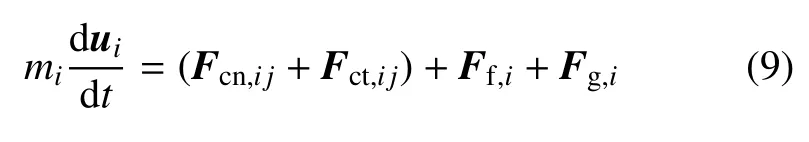
式中,mi为颗粒i质量,Fcn,ij和Fct,i j分别为颗粒i与颗粒j的法向和切向碰撞力,Fg,i为颗粒i重力,Ii为颗粒i的惯性矩,ωi为颗粒i的角速度,Mc为颗粒碰撞引起的力矩

1.2.3 颗粒运动轨迹

假设颗粒在任意t时刻,合力为F(t),速度为u(t),位置为(x(t),y(t),z(t)).此时颗粒的加速度为a(t)=F(t)/mi.当颗粒运动Δt后,其瞬时速度为[32]

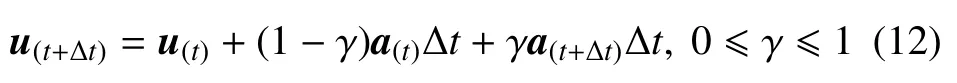
颗粒在t+Δt时刻的运动位移为

式中,γ 为插值系数,γ=0.5 为中心差分.

在空间直角坐标系下,颗粒在t+Δt时刻颗粒的位置为(x(t+Δt),y(t+Δt),z(t+Δt)),其计算公式为

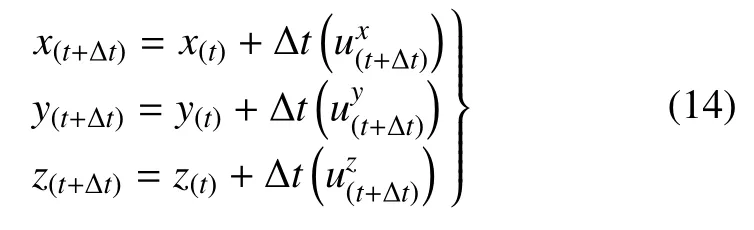
1.3 颗粒碰撞模型

颗粒碰撞过程的假设:(1) 颗粒是球形的刚体;(2)颗粒间只存在二体碰撞;(3)颗粒密度相同、直径可以不同,颗粒群初始状态为均匀分布.为了建立颗粒间碰撞的计算方法,不妨取颗粒群中任两颗粒记为颗粒i和颗粒j,设颗粒i直径为质量为mi、颗粒j直径为质量为mj,两颗粒质量比为q=mi/mj.

两颗粒发生碰撞满足动量定理,如图3 所示[33].

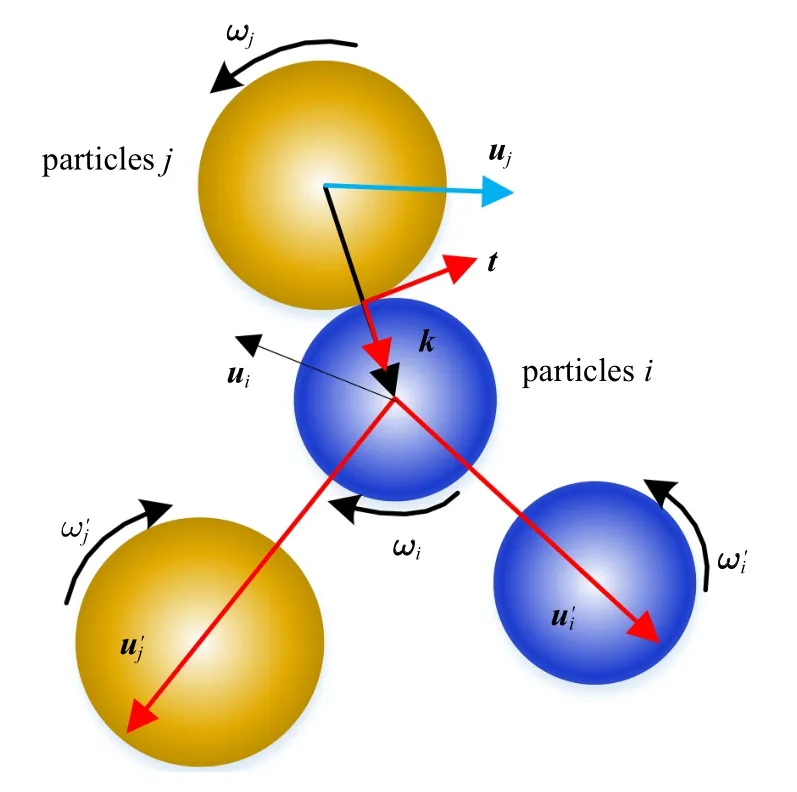
图3 颗粒碰撞示意图Fig.3 Schematic diagram of particle collision

式中,ui和为颗粒i碰撞前、后平动速度;ωi和为颗粒i碰撞前、后转动速度;k为颗粒相对速度的法向单位向量;J为颗粒碰撞时的冲量;Ii和Ij为颗粒i与颗粒j的转动惯量.

当两个颗粒碰撞后有滑移时,碰撞后平动速度和转动速度为

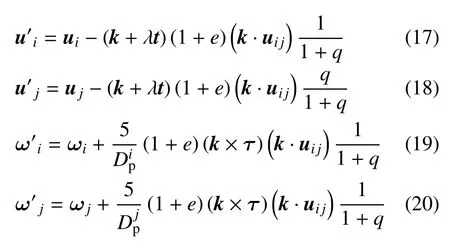
颗粒在碰撞时停止滑移,碰撞后平动速度和转动速度为

式中,λ 为摩擦系数,e为颗粒碰撞恢复系数,τ为颗粒相对速度的切向单位向量,uij为颗粒碰撞前相对速度,ui j,τ为颗粒碰撞前相对速度的切向分量.

颗粒碰撞时产生滑移满足下列条件

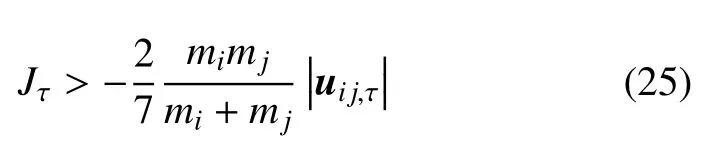
式中,Jτ为颗粒碰撞冲量的切向分量.

根据弹性力学碰撞理论[34],两颗粒碰撞时间tc为

根据冲量定理,可得两颗粒碰撞力计算公式为

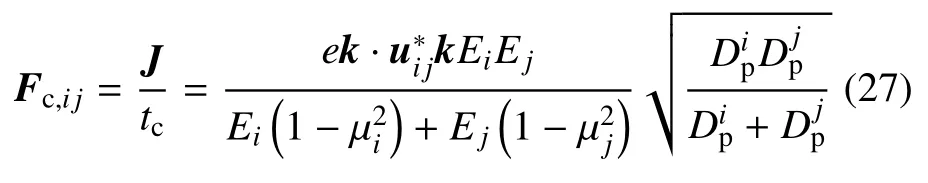
由式(15) 和式(16) 可知,两颗粒碰撞过程满足动量守恒,但碰撞过程能量发生耗散,不考虑颗粒旋转时的能量损失,则颗粒碰撞耗散能量为[35]

计算时间步内颗粒受到流体作用力的耗散能量为

由式(28)和式(29),得到颗粒i能量耗散率为

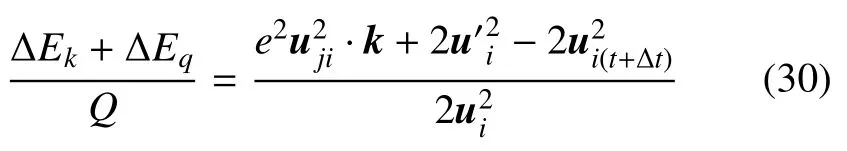
式中Q为碰撞前颗粒动能.

颗粒碰撞计算流程如图4 所示,碰撞颗粒i与颗粒j相对速度uij通过式(25) 判断颗粒是否发生滑移,若发生滑移则通过式(17)～式(20)计算颗粒碰撞后速度,若颗粒不发生滑移则通过式(21)～式(24)计算颗粒碰撞后速度.采用插值算法,将颗粒碰撞前相对速度uij与碰撞后相对速度进行加权插值得到代入式(26)和式(27)得到颗粒碰撞时间tc和碰撞力Fc,i j,然后将其代入式(9)和式(10)得到颗粒碰撞后的速度,并对碰撞后速度的设定和求得值进行比较判断,若不满足需修正碰撞后速度,重复式(26)、式(27)和式(9)、式(10)计算;否则,求得颗粒碰撞后速度值.其中,h为求解次数,为速度收敛容差.

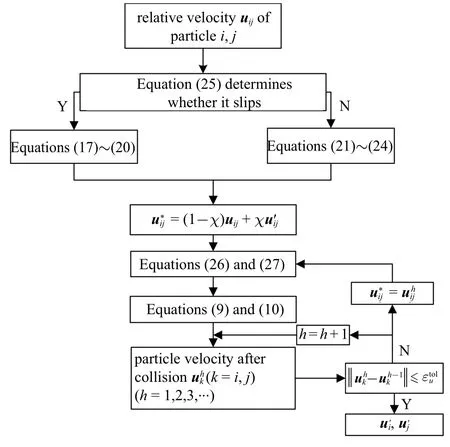
图4 颗粒碰撞后速度计算流程Fig.4 Calculation flowchart of velocity for Particle collision

1.4 耦合分析计算方法

颗粒位置变化直接导致流体体积分数和动量交换力源项的变化,因此,根据流体单元内流体体积分数和动量交换力源项的变化,建立流体与颗粒群耦合的收敛条件

CFD-DEM 耦合分析时,其耦合计算流程如图5所示,CFD 计算采用SIMPLE 算法求解流体域连续性方程和动量方程,根据颗粒和流体的相对速度,计算颗粒受到的流体作用力Ff,传递给DEM 求解器,并启动DEM 计算.DEM 采用牛顿第二运动定律求解颗粒运动方程,根据颗粒在Δtp的运动轨迹,搜索和判断颗粒碰撞,若颗粒产生碰撞,需修正颗粒计算时间步长.根据颗粒在计算域内位置和受力的变化计算得到流体的体积分数αf和动量交换力源项Sf,若不满足式(31)和式(32),传递给CFD 求解器,自动更新流体计算时间步长,并推进CFD 计算.

CFD 求解如图5(a) 所示,对流体计算域进行初始化,设置流体初始计算时间步长Δtf,判断流体是否满足收敛条件,若满足,CFD 求解结束.若不满足,缩短流体时间步Δtf=kn· Δtf(k≤1 为修正系数,n=1,2,3,··· 为流体时间步缩短次数),重新进行CFD 计算,直至满足流体收敛条件,CFD 求解结束.

CFD 求解结束后,计算Δtf时刻颗粒受到的流体力Ff传递给DEM,并启动DEM 求解.

DEM 求解如图5(b)所示,设置颗粒计算初始时间步长Δtp=Δtf,判断颗粒在Δtp时刻计算结果是否满足式(31)、式(32) 颗粒与流体耦合收敛条件,若不满足,缩短颗粒时间步=kn· Δtp,重新进行DEM 求解,直至满足耦合收敛条件,DEM 求解结束,此时耦合分析的时间步为若满足,根据颗粒在Δtp的运动轨迹,搜索和判断颗粒是否产生碰撞,若无碰撞,=Δtp,DEM 求解结束.若存在碰撞,计算得到最先发生碰撞的时间≤Δtp,并根据的颗粒位置,判断是否满足耦合收敛条件.若不满足,缩短颗粒求解时间重新进行DEM 求解,直至满足耦合收敛条件,DEM 求解结束,此时耦合分析的时间步为(其中i=1 时,时间步内第1 次搜索到碰撞,若满足,需判断碰撞累计时长是否满足若不满足,DEM 求解结束.若满足,则以剩余时间作为新的颗粒时间步长重新进行颗粒计算,并搜索颗粒碰撞,根据的颗粒位置,判断是否满足耦合收敛条件,若不满足,缩短颗粒求解时间重新进行DEM 求解,直至满足耦合收敛条件,DEM 求解结束,此时耦合分析的时间步为(其中i=2 时,时间步内第2次搜索到碰撞,若满足耦合条件,再次判断碰撞累计时长是否满足＜Δtp(i=2 时,若不满足DEM 求解结束.若满足,重新以剩余时间进行颗粒计算直至碰撞累计时长＜Δtp不成立,或者不满足耦合收敛条件,此时(时间步内进行n次碰撞)DEM 求解结束.

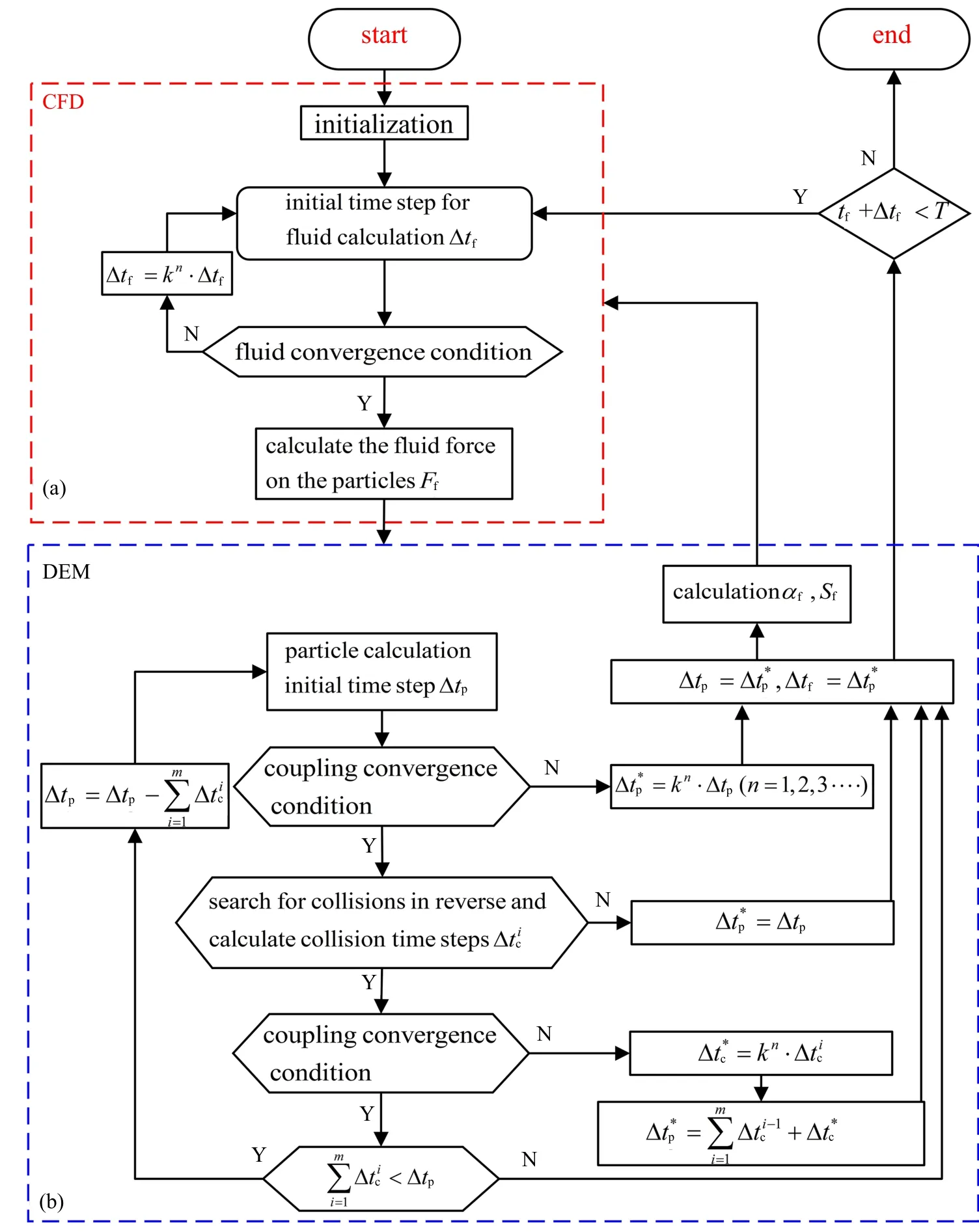
图5 CFD-DEM 耦合计算流程图Fig.5 Flow chart of CFD-DEM coupling calculation

DEM 求解结束后,计算流体体积分数αf和动量交换力源项Sf,并根据耦合分析时间步对颗粒和流体计算时间步进行修正Δtp=判断流体计算时间tf+Δtf＜T是否成立,若成立,将αf和Sf传递给CFD,重新开始CFD 求解;若不成立,则耦合计算结束.

其中,颗粒碰撞的搜索采用的是逆向迭代算法,增大计算时间步长不会影响颗粒碰撞搜索的计算精度.颗粒不发生碰撞时,计算时间步长的增大,使颗粒运动位移增大,导致流体计算单元内流体体积分数αf和动量交换力源项Sf变化过快,造成颗粒-流体耦合计算误差.式(31)和式(32)限制误差的大小,保证颗粒-流体耦合计算误差不随计算时间步长变化.

2 颗粒碰撞搜索的逆向迭代算法

流体内部的大量颗粒群随流体进行不规则运动,颗粒与颗粒、颗粒与壁面存在碰撞,快速、准确判断颗粒间发生碰撞,是提高颗粒与流体耦合计算效率的有效方法.

2.1 目标颗粒的变网格构造

在数值模拟颗粒间碰撞时,在一个时间步内颗粒只能与周边颗粒发生碰撞[36],将目标颗粒与周围可能发生碰撞的颗粒组成一个搜索空间网格进行碰撞搜索.具体方法如下:将目标颗粒在计算时间步的运动位移,作为空间网格对角线,建立搜索空间网格体,如图6(a) 所示.由于计算域内不同颗粒在Δt时间步内运动的位移不同,所构建的空间网格也会出现不同尺寸,即为变网格.

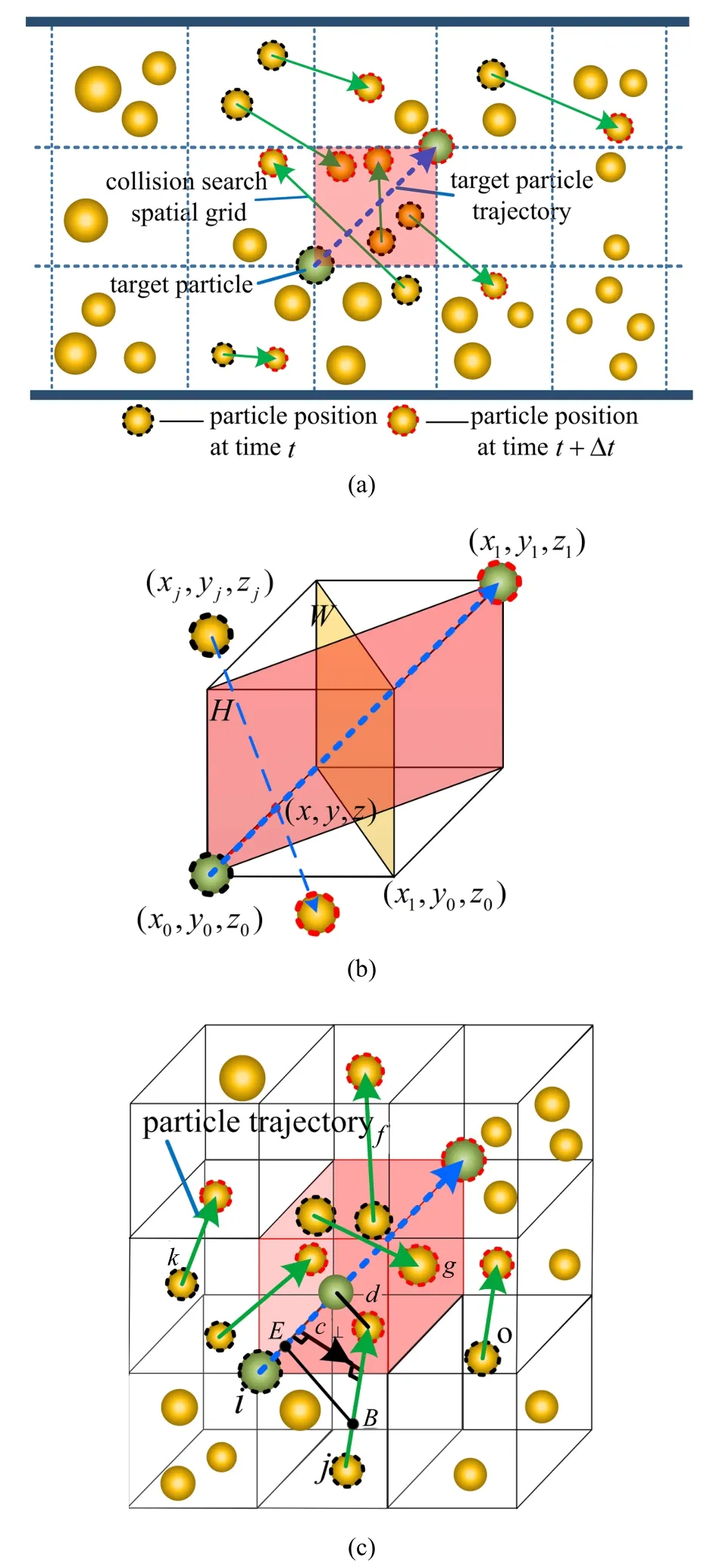
图6 颗粒碰撞搜索示意图:(a)变网格建立示意图;(b)颗粒运动轨迹穿过空间搜索网格示意图;(c)颗粒间距筛选示意图Fig.6 Search diagram of particle collision:(a)Schematic diagram of variable grid establishment;(b)schematic diagram of particle trajectories passing through the spatial search grid;(c)schematic diagram of particle spacing screening

2.2 目标颗粒碰撞列表建立

为了缩短颗粒碰撞搜索和判定时间,对目标颗粒周围颗粒筛选,保留与目标颗粒可能发生碰撞的颗粒,建立碰撞搜索列表,具体步骤如下.

(1)在计算时间步内,筛选运动轨迹与空间网格体存在交集的颗粒,如图6(a)所示.

设目标颗粒在t时刻和t+Δt时刻的坐标为(x0,y0,z0)和(x1,y1,z1),以此两点连线为对角线,构建目标颗粒的碰撞搜索空间网格体.

对计算域内任一颗粒j,从t到t+Δt时刻的运动轨迹与目标颗粒所建空间网格体若有交集,则可能产生碰撞;否则无碰撞.颗粒运动轨迹穿过空间网格体必定与空间网格体对角面H或W相交,因此计算颗粒运动轨迹与对角面的交点,并判断交点是否在空间网格体的范围内即可,如图6(b)所示.

不妨取颗粒j运动轨迹经过坐标(xj,yj,zj),且方向向量为m=(Xj,Yj,Zj),在H平面经过点(x0,y0,z0),法向量为n=(n1,n2,n3),运动轨迹与H平面交点o(x,y,z).

则颗粒j运动轨迹的参数方程为

式中φ 为参数.

H平面的点法式方程为

其中,颗粒j运动轨迹与H平面的交点o(x,y,z)一定满足式(33)和式(34),将式(33)代入式(34)得

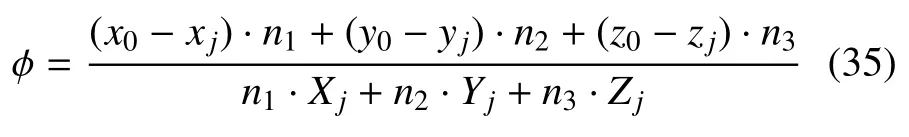
将φ 代入式(33) 得到交点o(x,y,z) 坐标,若交点坐标在空间网格体范围内,则说明运动轨迹穿过空间网格体.若交点坐标不在空间网格体范围内,或式(35) 分母为0 (运动轨迹与H平面平行),则运动轨迹与H平面不相交.需用相同方法判断运动轨迹与W平面是否相交,若运动轨迹与W平面相交,说明运动轨迹穿过空间网格体.

(2)依据颗粒与目标颗粒运动轨迹间距离小于或等于两颗粒半径之和的条件,再次筛选可能碰撞颗粒,如图6(c)所示.

目标颗粒i运动轨迹方向向量为e=(Xi,Yi,Zi),颗粒j运动轨迹方向向量为b=(Xj,Yj,Zj).将e×b=c⊥得到向量e,b的公垂向量c⊥=(X,Y,Z).

取目标颗粒i运动轨迹上任意一点E和颗粒j运动轨迹上任意一点B,得到向量eb,将向量eb在公垂向量c⊥方向上做投影,得到目标颗粒i与颗粒j运动轨迹间最短距离d如下

在计算时间步内,若两颗粒运动轨迹最近距离d≤则目标颗粒i可能与颗粒j发生碰撞,颗粒j保留.若d＞则目标颗粒i不会与颗粒j发生碰撞.

经(1)(2)两步筛选后,保留下来的颗粒形成目标颗粒碰撞搜索列表.

2.3 碰撞颗粒的逆向搜索算法

在提高颗粒碰撞计算效率时,采用了较大的计算时间步Δtp后,为了解决颗粒碰撞漏判状况,沿颗粒走过的运行轨迹采用逆向搜索方式,搜索判断两颗粒是否存在碰撞.若不存在,说明该时间步内计算结果正确,可进行下一个时间步计算,若存在碰撞,确定发生碰撞时间,修正颗粒计算时间步.

如图7 所示,假设在计算时间步Δtp内存在t+Δtc时刻,颗粒i与颗粒j产生碰撞.根据颗粒运动轨迹计算方法,得到颗粒i与颗粒j在时间增量为Δtc时颗粒的位置坐标为

图7 颗粒碰撞时间求解示意图Fig.7 Schematic diagram of particle collision time solution

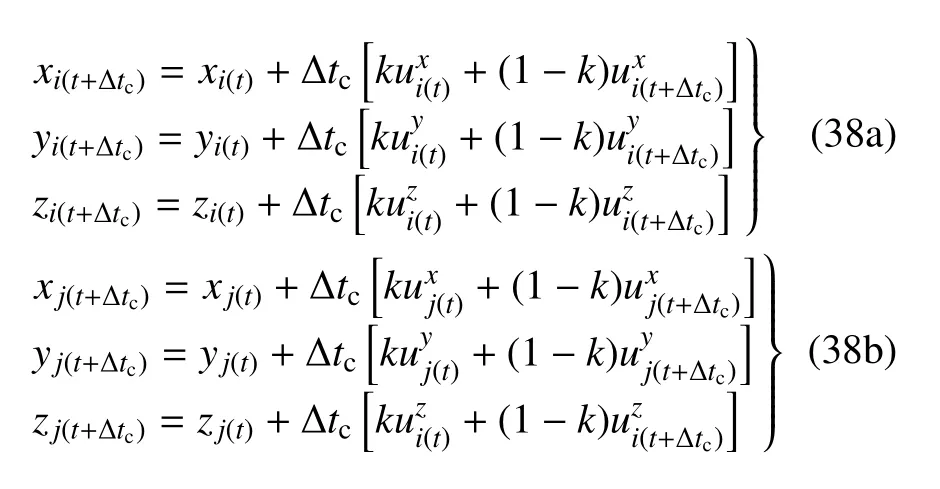
颗粒i与颗粒j在Δtc处的距离和发生碰撞条件为

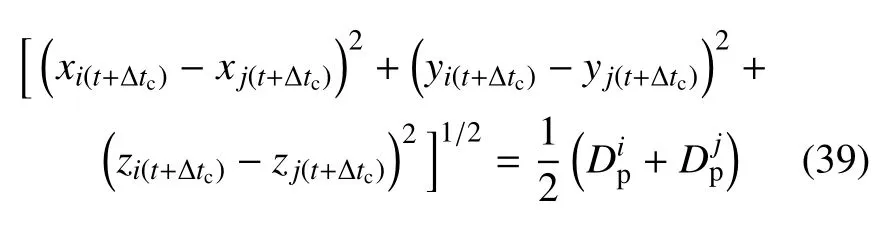
方程中颗粒i和颗粒j在t时刻的速度和坐标均为已知,方程可化简成一元四次方程

对方程求解得到Δtc1,Δtc2,Δtc3,Δtc4四个解,依据条件,判断解的有效性.若存在真解,取最小值作为颗粒i与颗粒j碰撞时间步.若无真解,说明颗粒在计算时间步内不发生碰撞.

在一个计算时间步内,假设目标颗粒i与碰撞列表内颗粒mi发生碰撞,其碰撞时间步为1,2,···,m).因只考虑颗粒二体碰撞,最早与目标颗粒相遇的颗粒k才是发生碰撞的颗粒,则碰撞时间步取为

2.4 颗粒群碰撞求解流程

对于由n个颗粒组成的颗粒群,依据前述方法,可选择n-1 个目标颗粒,完成n-1 个变网格和碰撞搜索列表建立.假设目标颗粒i对颗粒j进行搜索判断后建立碰撞搜索列表,颗粒j作为目标颗粒进行列表建立时,无需对颗粒i重新进行判断,直接从总的碰撞列表内映射即可.

将每个列表内的最小碰撞时间步长,放入总表内,得到最小碰撞时间步,局部求解域的计算时间步逆向到最先发生碰撞时刻,执行碰撞.碰撞计算完成后,碰撞颗粒重新更新碰撞列表,并计算最小碰撞时间步长,其他未发生碰撞颗粒,只需在原有碰撞时间步长基础上减去已经完成的碰撞时间步长,更新碰撞时间步总表.颗粒群碰撞求解流程如图8 所示.

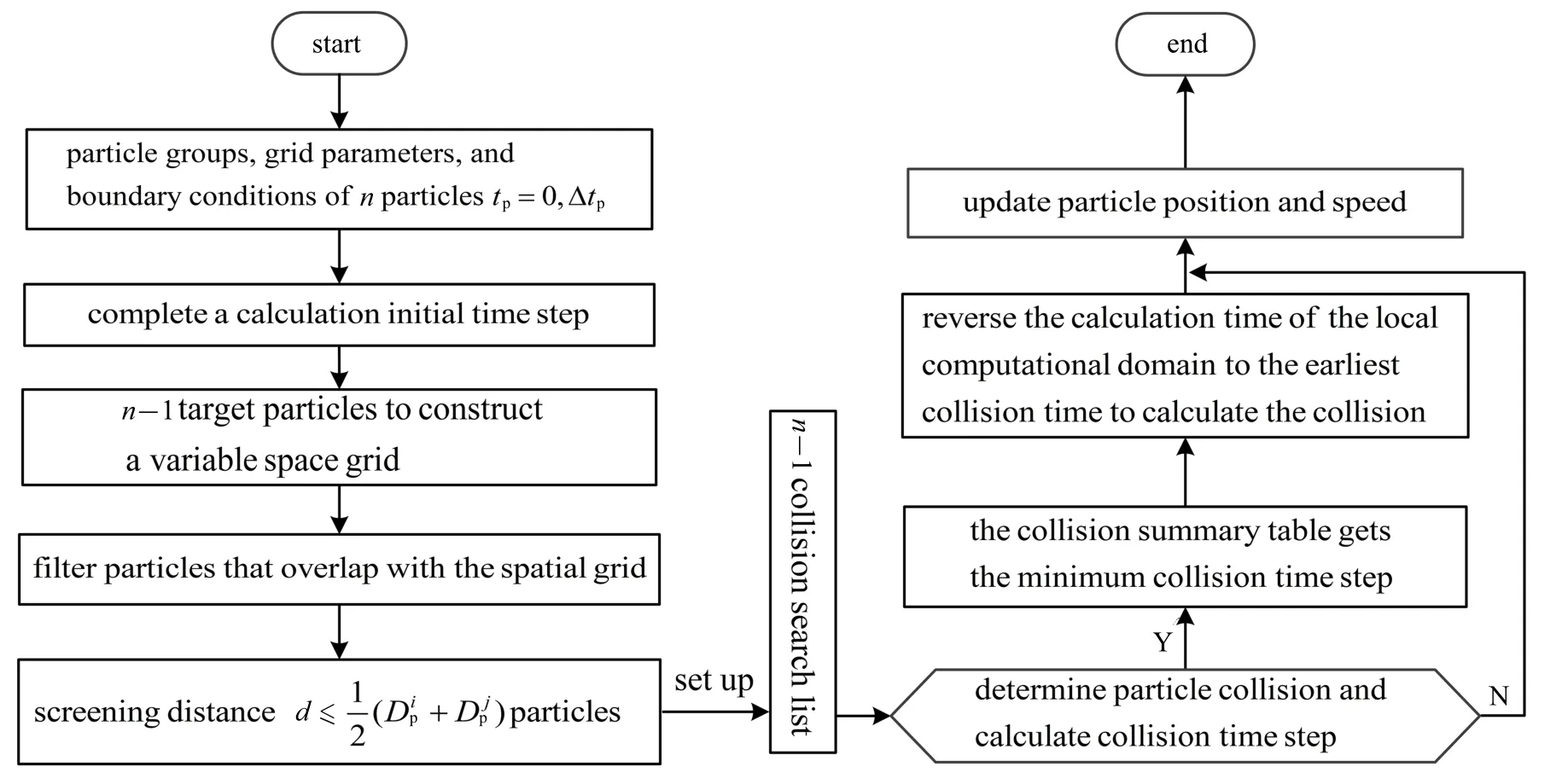
图8 颗粒群碰撞搜索求解流程Fig.8 Particle swarm collision search solution process

3 CFD-DEM 耦合分析及颗粒碰撞搜索算法验证

基于Fluent 和DEM 平台,采用Delphi 编程二次开发了流体与颗粒群耦合动力学分析程序.

3.1 两个颗粒碰撞算例

采用现有的DEM 软件和本文提出的改进颗粒碰撞搜索算法MDEM 分别对两个颗粒碰撞进行数值模拟.预期验证本文方法的计算精度和计算效率.

如图9 所示,取A,B两颗粒的半径R=5 mm,弹性模量为210 GPa,泊松比为0.27,A颗粒初始速度=2 m/s,=-2 m/s,B颗粒初始速度=2 m/s,A,B颗粒初始圆心间距100 mm.为了便于讨论,记和分别为A,B颗粒碰撞后x,y方向速度,Fcn为A,B颗粒的碰撞力.工况1:A,B颗粒匀速运动.工况2:A,B颗粒变速运动,沿x方向加速度为-10 m/s2,沿y方向加速为-10 m/s2.根据颗粒碰撞理论和解析解,得到A,B颗粒的碰撞速度、碰撞位置和发生碰撞的时间、碰撞力如表1所示.

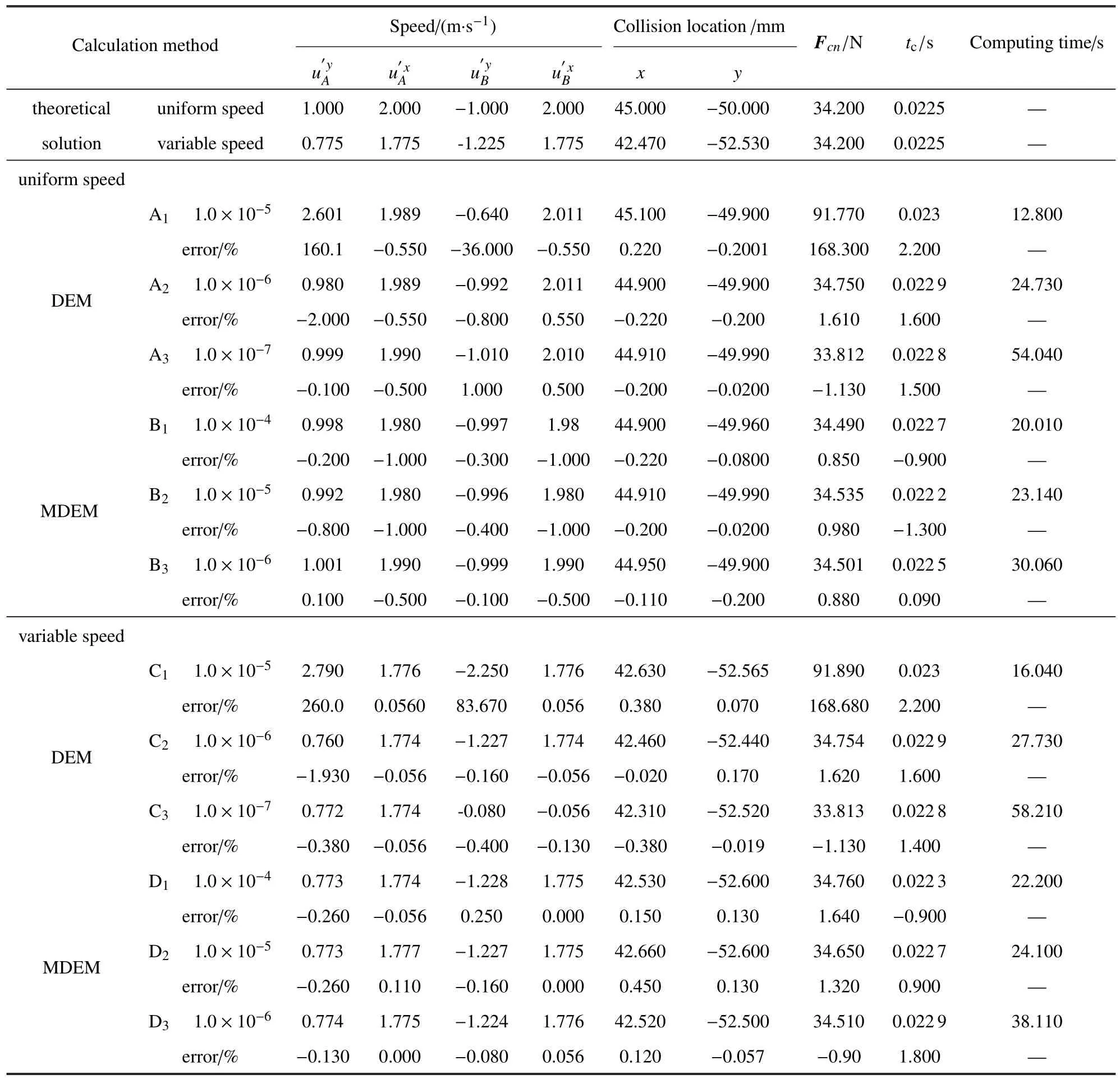
表1 两颗粒运动及碰撞的理论和数值模拟结果Table 1 Theoretical and numerical simulation results of movement and collision of two particles

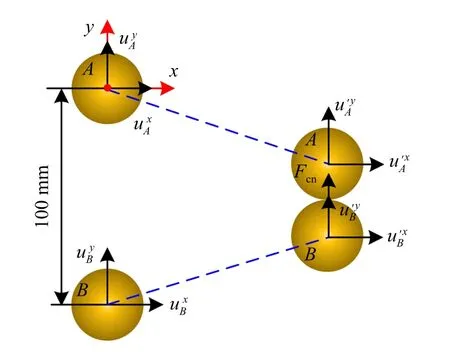
图9 颗粒位置示意图Fig.9 Schematic diagram of particle position

DEM 和MDEM 取计算时间0.1 s,计算时间步为10-4s,10-5s,10-6s,10-7s 对颗粒匀速、变速运动进行数值模拟,得到碰撞力、碰撞速度、碰撞位置等结果一并列入表1.模拟所用计算机为英特尔Core i7-9700 @ 3.00 GHz 八核,主显卡AMD Radeon RX 550 Series,内存16 GB.

由图10 可知,在匀速工况下,采用DEM 方法,只有当计算时间步在10-6s 及以下,得到的计算结果与理论解误差才不大于2%,其中速度最大误差为2%和1%,碰撞位置最大误差均为0.2%,碰撞力误差为1.61%和1.13%,发生碰撞时刻误差为1.6%和1.5%,A2和A3计算耗时分别为24.73 s 和54.04 s.由此可见,DEM 方法的计算精度受计算时间步影响较大,计算效率随着时间步的减小而显著降低.采用MDEM 方法,不同计算时间步得到的计算结果与理论结果误差均小于2%,其中速度最大误差为1%,1%,0.5%,碰撞位置最大误差均为0.22%,0.2%,0.2%,碰撞力误差为0.85%,0.98%,0.88%,发生碰撞时刻误差为0.9%,1.3%,0.09%,B1,B2,B3计算耗时分别为20.01 s,23.14 s,37.06 s.由此可见,本文提出的MEDM方法,计算精度不受计算时间步的影响,且随着时间步的减小计算效率呈下降趋势,其中B2计算时间步长比A2计算时间步长大一个量级,计算耗时缩短4.59 s (6.4%).B1计算时间步长比A2计算时间步长大两个量级,计算耗时缩短4.72 s(19.1%).

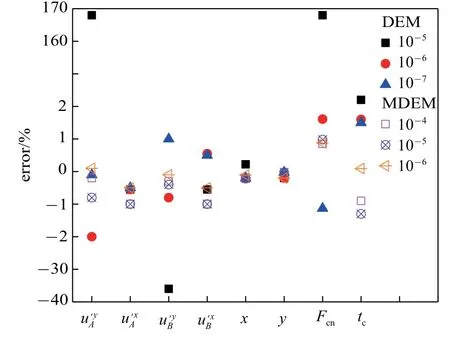
图10 两颗粒匀速运动误差分析图Fig.10 Error analysis diagram of two particles in uniform motion

由图11 可知,在变速工况下,采用DEM 方法,只有当计算时间步在10-6s 及以下,得到的计算结果与理论解误差均小于2%,其中速度最大误差为1.930%和0.400%,碰撞位置最大误差均为0.17%和0.38%,碰撞力误差为1.62%和1.13%,发生碰撞时刻误差为1.6%和1.4%,C2和C3计算耗时27.73 和58.21s.采用MDEM 方法,不同计算时间步得到的计算结果与理论结果误差均小于2%,其中速度最大误差为0.26%,0.26%,0.13%,碰撞位置最大误差均为0.15%,0.45%,0.12%,碰撞力误差为1.64%,1.32%,0.9%,发生碰撞时刻误差为0.9%,0.9%,1.8%,D1,D2,D3计算耗时22.2 s,25.1 s,38.11 s.D2计算时间步长比C2计算时间步长大一个量级,计算耗时缩短2.63 s(9.48%),D1计算时间步长比C2计算时间步长大两个量级,计算耗时缩短5.53 s(19.9%).由此可见,两种方法在模拟变速运动时的结论和规律同匀速运动.

图11 两颗粒变速运动误差分析图Fig.11 Error analysis diagram of variable speed movement of two particles

综上所述,采用本文方法对颗粒匀速、变速运动进行数值模拟,选取不同时间步均能得到近似的计算结果,当计算时间步比DEM 大两个量级时,匀速运动的计算效率提高19.1%,变速运动的计算效率提高19.9%,使时间步选取过小、计算效率低的问题得到有效解决.

3.2 多个颗粒碰撞算例

颗粒几何形状、材质属性同3.1 算例.颗粒初始位置如图12 所示,水平设置6 个颗粒,颗粒间距20 mm,编号h1,h2,h3,h4,h5,h6,其中h1,h3,h5颗粒水平速度均为0 m/s,垂直向下速度均为2 m/s,h2,h4,h6颗粒水平和垂直速度均为2 m/s.竖直设置6 个颗粒,颗粒间距20 mm,编号v1,v2,v3,v4,v5,v6,其中v1,v3,v5颗粒水平速度均为2 m/s,垂直速度均为0 m/s,v2,v4,v6颗粒水平和垂直速度均为2 m/s,颗粒做匀速运动.

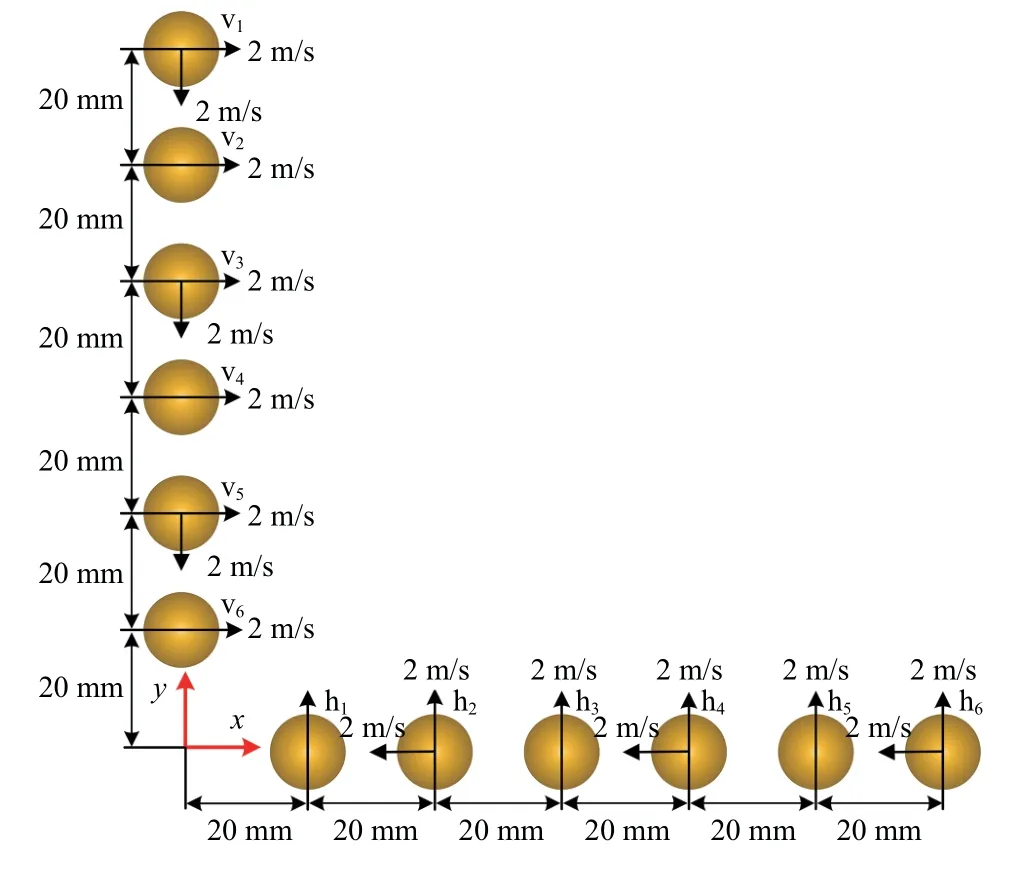
图12 多颗粒碰撞初始位置示意图Fig.12 Schematic diagram of initial position of multi-particle collision

采用理论分析,可得6 对颗粒h1–h2,h3–h4,h5–h6,v1–v2,v3–v4,v5–v6首次发生碰撞时刻为0.005 0 s,碰撞位置分别为(25,10),(65,10),(105,10),(10,25),(10,65),(10,105),后继颗粒碰撞较复杂,无法得到理论解.在DEM 和MDEM 数值模拟中,分别选取计算时间步为10-5s,10-6s,10-7s 和10-4s,10-5s,10-6s,计算时间取0.1 s.

由 DEM 数值模拟结果可知,计算时间步为10-5s 得到23 次颗粒对碰撞,而计算时间步为10-6s和10-7s,得到25 次颗粒对碰撞,部分结果见表2.由图13 可知,在10-6s 和10-7s 计算时间步得到的首次发生碰撞时刻、碰撞位置与理论解的误差均不大于2%.计算耗时分别为60.31 s 和90.12 s.由此可见,计算时间步取10-5s 时,DEM 方法漏判了2 次颗粒碰撞,随着计算时间步的减小,多颗粒碰撞数值模拟的计算效率降低.

图13 DEM 颗粒碰撞时间、位置误差分析图Fig.13 DEM particle collision time and position error analysis diagram

由MDEM 数值模拟结果可知,计算时间步取10-4s,10-5s,10-6s 时,均得到25 次颗粒对碰撞,部分结果如表2 和表3 所示.由图14 可知,不同计算时间步得到的首次发生碰撞时刻、碰撞位置与理论解的误差均不大于2%.计算耗时分别为51.31 s,56.22 s,65.21 s.由此可见,在模拟多颗粒碰撞时,MEDM 方法的计算精度不受计算时间步大小影响,可采用较大的时间步来提高计算效率.

图14 MDEM 颗粒碰撞时间、位置误差分析图Fig.14 MDEM particle collision time and position error analysis diagram

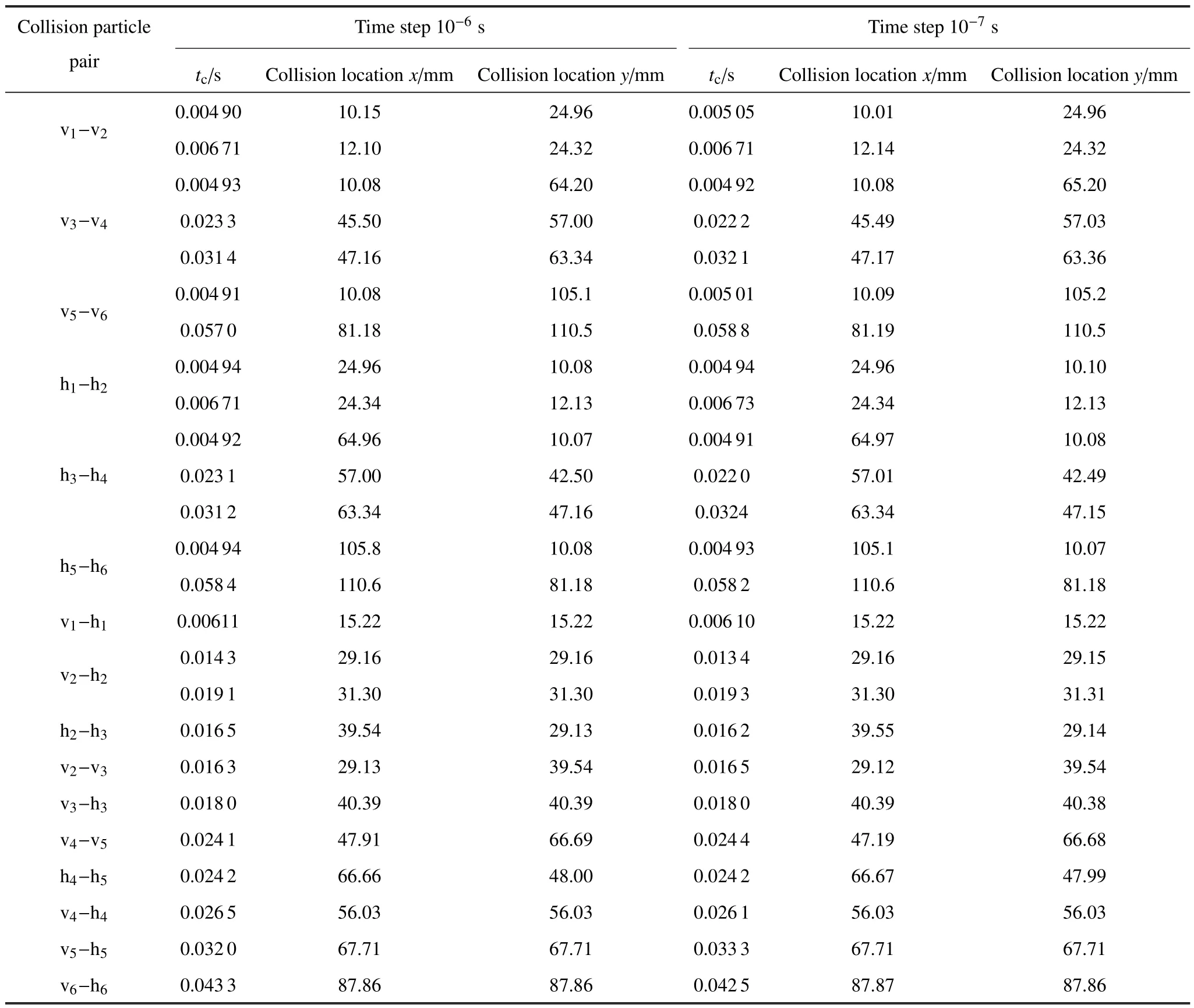
表2 多颗粒运动及碰撞的数值模拟结果(DEM)Table 2 Numerical simulation results of multi-particle motion and collision(DEM)

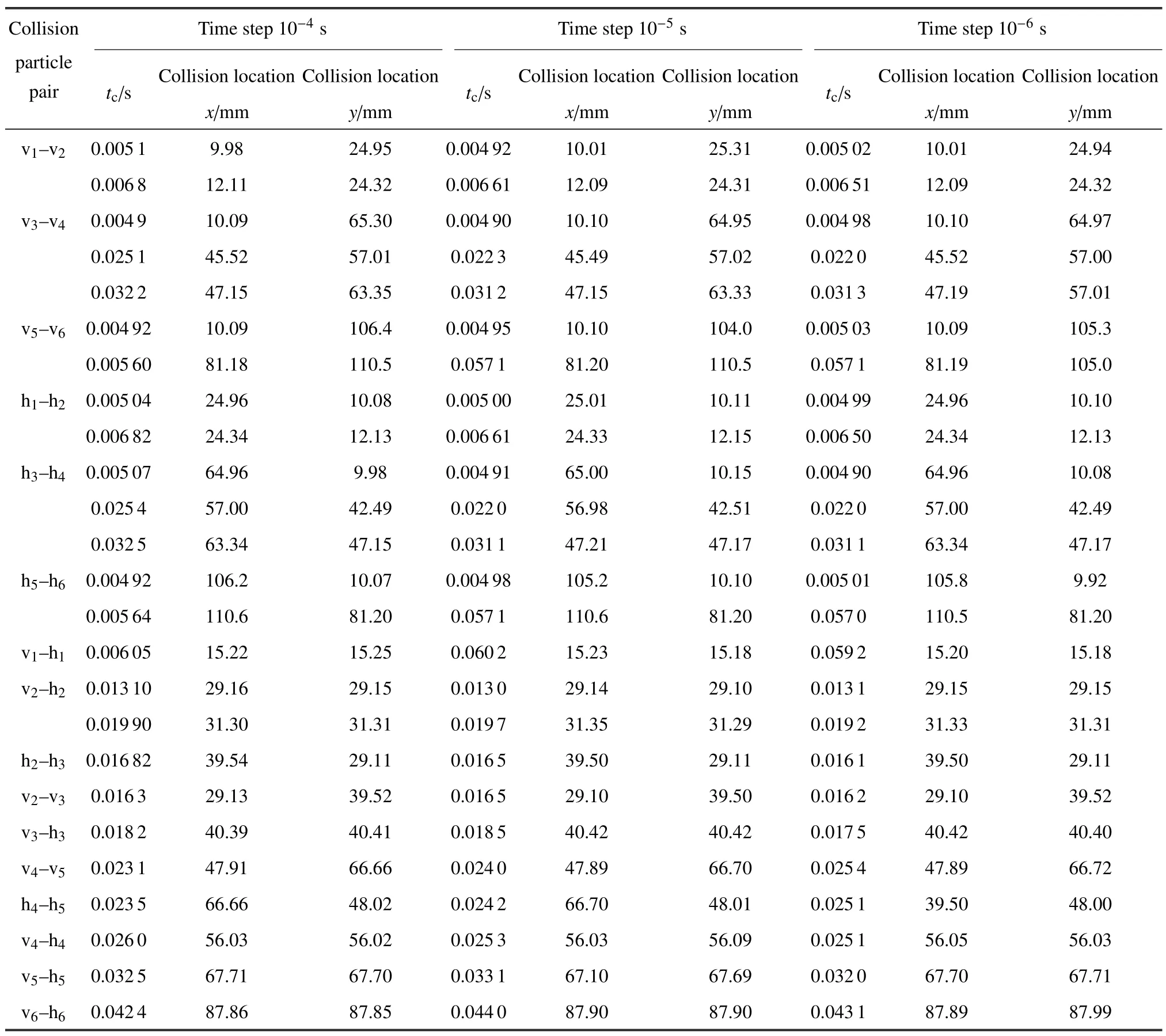
表3 多颗粒运动及碰撞的数值模拟结果(MDEM)Table 3 Numerical simulation results of multi-particle motion and collision(MDEM)

当DEM 和MDEM 计算时间步均取10-6s 时,MDEM 比DEM 计算时间增加4.9 s,这是由于每个计算时间步内的逆向搜索耗时所致.当MDEM 的计算时间步扩大一个量级(10-5s) 时,比DEM 计算时间缩短4.09 s,即计算耗时降低了6.8%;当MDEM 的时间步取10-4s 时,比DEM 计算时间缩短了9 s,即计算耗时降低了14.9%.其中h4,v4,h2,v2均发生5 次碰撞,运动轨迹如图15 所示,虚线为MDEM,实线为DEM.

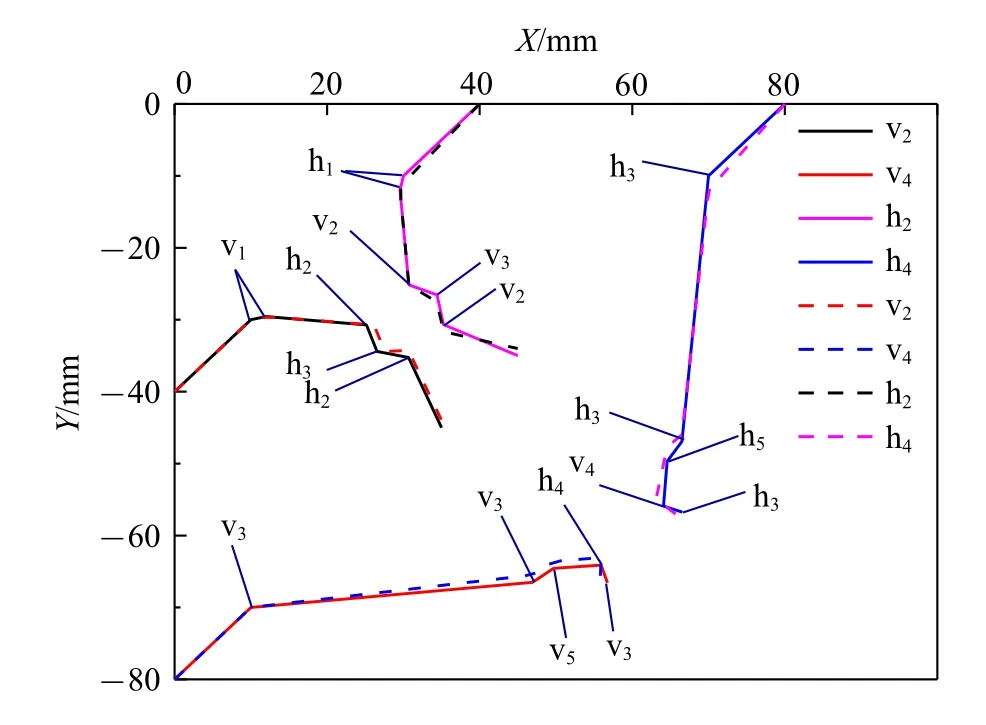
图15 多颗粒运动轨迹与碰撞示图Fig.15 Movement trajectories and collisions of more than one particle

综上所述,采用本文方法选取10-6s,10-5s,10-4s 时间步对多个颗粒碰撞进行数值模拟,均能得到精确的计算结果,计算时间步选取可比DEM 方法大两个量级,其计算耗时降低了14.9%.

3.3 CFD-DEM 耦合分析算例

采用CFD-DEM 和CFD-MDEM 方法分别对3.2算例中的多个颗粒与流体耦合进行数值模拟.计算流体域为300 mm×300 mm×300 mm 的矩形域,流体密度ρ=1 g/cm3、黏度μf=0.1 g/(cm·s),流体初始状态为静止.计算域采用规则的矩形网格离散,除上部边界设置为开边界外,其余壁面采用无滑移边界条件.颗粒几何参数、材质、初始位置及计算参数等与算例3.2 完全相同,CFD-DEM 流体计算时间步长设置为颗粒计算时间步长的10 倍.CFD-MDEM 颗粒计算初始时间步长与流体计算初始时间步相等,颗粒与流体真实计算时间步在耦合计算过程中,根据耦合收敛条件实时调整和修正,时间步长设置如表4所示.

表4 颗粒与流体耦合分析的时间步长设置Table 4 Time step setting of particle-fluid coupling analysis

CFD-DEM 计算结果表明:在A1,A2,A3计算时间步得到颗粒碰撞次数分别为18 次、22 次、22次,与算例3.2 相比碰撞次数减少了3 次,原因在于流体的阻力使颗粒做减速运动,计算耗时分别为18 min,27 min,42 min,只有在颗粒计算时间步小于等于10-6s 时,CFD-DEM 耦合计算才能得到精确值.

CFD-MDEM 计算结果表明:在B1,B2,B3计算时间步,得到的颗粒碰撞次数均为22 次,计算耗时分别为22.5 min,24 min,31 min,颗粒计算初始时间步的改变不影响CFD-MDEM 耦合计算精度.

A2流体计算时间步比B3流体计算初始时间步大一个量级,A2流体求解器启动104次,颗粒求解器启动105次,B3流体与颗粒求解器均启动100 383 次.B3比A2多启动383 次,是由于MDEM 算法根据耦合收敛条件,修正计算初始时间步,得到真实计算时间步比计算初始时间步小,B3比A2计算多耗时4 min.B2流体计算初始时间步与A2流体计算时间步相等,B2颗粒计算初始时间步比A2颗粒计算时间步大一个量级,B2流体与颗粒求解器启均动11 479 次,与A2流体求解次数相比求解器多启动1479 次,与B3相比求解器多启动次数由383 次增加到1479 次,是由于颗粒计算初始时间步的扩大,颗粒求解不满足收敛条件次数增多造成.B2比A2计算少耗时3 min,降低11.1%.B1流体计算初始时间步比A2流体计算时间步大一个量级,颗粒计算初始时间步比A2颗粒计算时间步大两个量级,B1流体与颗粒求解器均启动3254 次,比A2计算少耗时4.5 s,降低16.7%.A2和B1颗粒h2,h3,h4和v2,v4,v6的运动轨迹基本一致,如图16 所示.

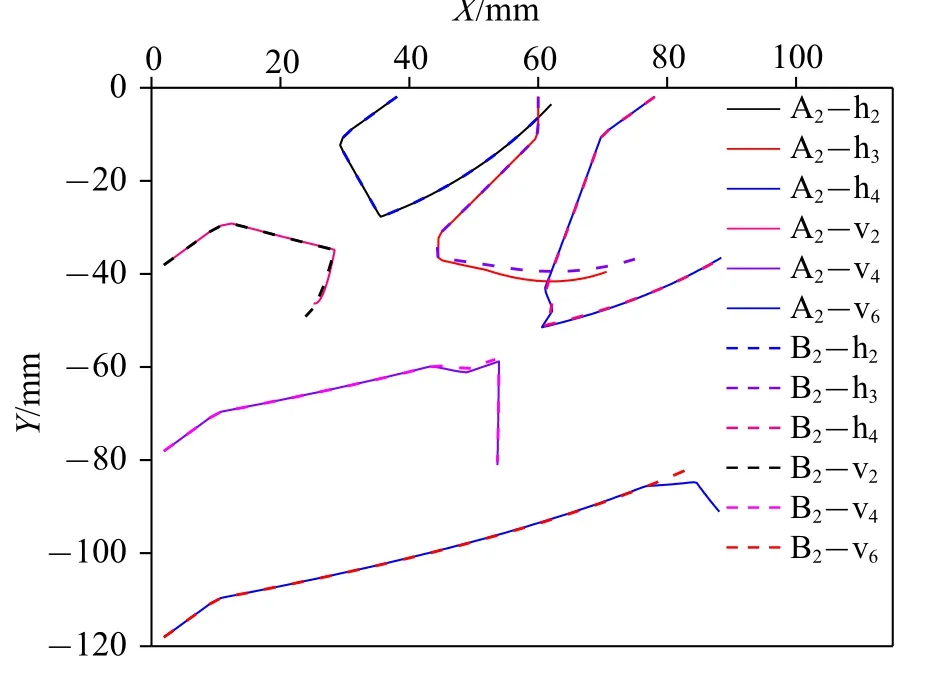
图16 颗粒运动轨迹Fig.16 Multiple particle trajectories in fluid

综上所述,采用CFD-MDEM 方法对多个颗粒与流体进行耦合数值模拟,流体与颗粒计算初始时间步取10-4s,10-5s,10-6s 均能得到精确的计算结果,计算耗时比CFD-DEM 方法降低了16.7%.

4 结论

本文针对CFD-DEM 耦合计算中,颗粒时间步选取过小、计算效率低,时间步选取过大、碰撞颗粒漏判的问题,通过算法研究和算例验证,取得如下结论和认识.

(1)提出了颗粒碰撞搜索的改进算法,以目标颗粒运动位移构建可变空间搜索网格,筛选可能碰撞颗粒建立搜索列表,减少了颗粒碰撞的搜索时间;采用逆向搜索方式判断颗粒碰撞,避免了时间步选取过大对颗粒碰撞漏判,确保了颗粒碰撞的准确描述.通过两个颗粒和多个颗粒的运动和碰撞算例表明,本方法计算时间步选取的大小对颗粒碰撞计算精度影响不大;两个颗粒在匀速和变速工况下的数值模拟计算耗时比DEM 方法降低了19.1%和19.9%,多个颗粒的数值模拟计算耗时比DEM 方法降低了14.9%.

(2)建立了颗粒与流体计算时间步自动调整的耦合算法,颗粒与流体计算初始时间步选取可以相同,根据颗粒推进时间实时调整流体计算时间,实现流体计算时间步随颗粒计算时间自动调整,提高了颗粒与流体耦合的计算效率.多个颗粒与流体耦合算例的数值模拟表明,该算法的计算精度受颗粒和流体的初始计算时间步长影响较小,可通过较大的颗粒时间来提高计算效率,该算法在求解算例的耗时比CFD-DEM 方法降低了16.7%.