串列布置三圆柱涡激振动频谱特性研究1)

涂佳黄 胡 刚 谭潇玲 梁经群 张 平

(湘潭大学土木工程与力学学院,湖南湘潭 411105)

引言

涡激振动现象广泛存在于实际工程中,当柱体结构处于流场时,交替的涡脱落在结构表面产生周期性的流体力,导致结构产生振动.当海洋立管[1-2]、桥梁结构[3-4]、高层建筑[5-6]结构振动频率接近于自身固有频率时,结构会发生“锁定”现象[7],诱发结构产生较大的振动幅度,带来灾难性后果.另一方面,强烈的结构振动可以进行能源转换和利用[8-9].因此,有关涡激振动问题一直是研究者们所关注的热点之一.

目前,学者们对单圆柱涡激振动问题进行了相关研究,取得了一系列成果[10-13].与单圆柱涡激振动问题相比,串列多圆柱涡激振动情况更加复杂,对实际工程的参考意义更大.Papaioannou 等[14]研究了不同间距比工况下串列双圆柱涡激振动问题,发现间距比较小时,上游圆柱的锁定区间范围较单圆柱工况明显扩大且最大振幅增大,超过临界间距比后,下游圆柱对上游圆柱振幅的影响较小.Prasanth 等[15]对Re=100 和L=5.5D工况串列双圆柱进行了数值模拟研究,发现下游圆柱的锁定区间受到了上游圆柱的影响,明显大于单圆柱涡激振动的现象.及春宁等[16]对低雷诺数下串列双圆柱涡激振动中下游圆柱大振幅响应的耦合机制进行了全面分析,发现上游圆柱脱落漩涡激励下游圆柱大振幅响应的机理来自于脱落漩涡所诱发的位于下游圆柱的运动方向上低压区.Mysa 等[17]研究了L=(1.0～4.0)D,Re=100下串列双圆柱涡激振动中对响应起关键作用的因素,发现上游圆柱尾流与下游圆柱之间的耦合作用的强弱取决于横流向流体力与圆柱位移之间的相位差,与下游圆柱运动同相的部分对其响应起到了促进作用.Mittal 等[18]通过数值模拟发现Re=100,L=5.5D时上游圆柱的振动响应趋近于单圆柱涡激振动,而下游圆柱经历了大振幅振动.

关于串列三圆柱涡激振动问题,圆柱体之间相互作用对振动影响很大,潜在的机理也值得更多的努力去研究.Igarashi 和Suzuki[19]通过试验研究了L=(1.0～4.0)D,Re=10 900～39 200 的串列三圆柱绕流特性,根据下游圆柱上从上游圆柱分离的具有动态效应的剪切层,将6 种尾流模态进行了分类,并得到了发生双稳态现象的区域.Yu 等[20]通过研究发现三圆柱系统的振动响应剧烈,横流向最大振幅提高了25%.同时,结构运动轨迹大多呈现为不规则形状.Chen 等[21]对Re=100,L=(1.2～5.0)D工况下串列三圆柱进行数值模拟研究,发现L=1.2D时,串列三圆柱均表现为驰振现象.指出驰振现象的3 个关键因素是平衡位置偏移、低频振动以及漩涡脱落与圆柱之间的时机.Mahmoud 和Atef[22]对串列布置三圆柱系统的流致振动问题进行了研究,着重分析了上中游两静止圆柱体间距比的变化对下游圆柱体动力响应及其流场特性的影响.张志猛等[23]对Re=100 时上游圆柱固定串列三圆柱涡激振动进行数值模拟研究,发现当振幅较小时,上游圆柱的剪切层将三圆柱包裹在一起,尾流表现为单钝体脱涡模式.当振幅较大时,上游圆柱的旋涡重附着于下游圆柱上,尾流呈现出两列并排的漩涡.Behara 等[24]对串列布置三圆柱进行数值模拟分析,对于下游两圆柱根据其振幅和频率的响应,将约化速度划分为3 个区间:初始激励区、上锁定区、下锁定区.涂佳黄等[25]对Re=100下剪切来流作用下串列三圆柱体双自由度流致振动问题进行了数值计算研究,随固有频率比的增大,上游圆柱顺流向锁定区间范围会减小,而中下游圆柱双向锁定区间会扩大.

综上所述,频谱特性分析在多柱体结构涡激振动问题中的研究讨论较少,本文基于四步半隐式特征线分裂算子有限元方法,对均匀来流作用下串列布置三圆柱系统双自由度涡激振动问题进行了数值模拟,重点分析了圆柱体功率谱密度随不同雷诺数、固有频率比、约化速度的变化规律,对不同工况下功率谱密度的形态进行对比,深入研究了功率谱密度对结构动力响应的影响并揭示了其内在机理.为实际工程应用提供参考依据.

1 流固耦合数值方法

1.1 流体控制方程

基于ALE 方法下的不可压缩黏性流体的N-S 方程的无量纲形式表达如下

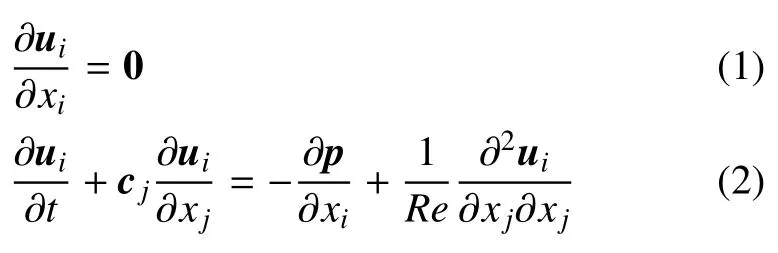
式中,xi为空间坐标;ui为流体速度;cj=uj-wj,cj为流体相对于网格移动速度的对流速度,wj为网格移动速度;p为流体压力;t为时间;Re=U∞D/ν,Re为雷诺数,D与U∞分别为特征长度尺寸与特征速度,ν为动力黏性系数.

1.2 固体控制方程

弹性支撑结果运动体系可假设为之质量-阻尼-弹簧系统,考虑双自由度运动的控制方程量纲归一化的形式如下

式中,X与Y分别为结构顺流向和横流向无量纲位移;ξ 为结构阻尼系数,为了得到最大结构位移响应,取ξ=0;Ur,x=U∞/(fn,xD) 和Ur,y=U∞/(fn,yD)和分别为x方向(顺流向) 与y方向(横流向) 约化速度,其中fn,x和fn,y分别为弹性支撑圆柱体结构的顺流向和横流向自然频率;和分别为阻力系数和升力系数;mr=m/(ρD2)为结构折合质量,其中m为单位长度结构质量,ρ 为流体密度.本文采用Newmark-β 时间积分法求解结构动力方程.

1.3 网格更新

为了避免网格失效问题,本文采用改进Laplace方程的边值问题方法对网格坐标进行更新[26]

式中,Si为网格节点i方向位移;Γm和Γf分别为网格动边界和固定边界;gi是运动边界上的节点位移;τ 是网格形变控制参数,表达式如下

式中,Δe为计算网格单元的面积(或体积);Δmin和Δmax分别为网格单元中最小与最大的面积(或体积).本文采用Galerkin 有限元方法求解该Laplace 方程的边值问题.

1.4 计算流程

本文采用分区迭代方法求解钝体结构涡激振动问题,该算法的计算流程如下:

(1) 求解流体控制方程.运用基于四步半隐式CBS 稳定化有限元方法求解流体控制方程式(1) 和式(2),获得t(n+1)时刻流场速度与压力,从而得到流体作用于结构上的流体力.

(2) 求解固体控制方程.将流体力施加到结构,以Newmark-β 时间积分方法求解结构运动控制方程式(3),得到t(n+1)时刻结构的动力响应.

(3) 网格更新.采用Galerkin 有限元方法求解Laplace 方程,获得网格节点位移及网格速度,并更新网格坐标.

(4)返回第一步开始计算t(n+2)时刻,并循环至系统达到稳定为止.

本文的数值方法已运用于涡激振动相关问题求解过程中[25,27-28],并能得到较好的数值结果,验证其正确性与可靠性.

2 问题描述

2.1 计算模型

为了研究上游结构尾流充分发展后对下游结构振动响应的影响,选取圆柱体结构间距比Lx=5.5D.其他参数为:雷诺数Re=80,100,160,固有频率比r=fn,x/fn,y=1.0,1.5,2.0,约化速度Ur=Ur,x=3～21,质量比mr=2.0.计算域尺寸为[-30D,60D]×[-20D,20D],上游圆柱(upstream cylinder,UC)、中游圆柱(midstream cylinder,MC) 和下游圆柱(downstream cylinder,DC)的圆心位置分别为(-5.5D,0)、(0,0) 与(5.5D,0),本文计算域堵塞率B=5%,如图1 所示.边界条件设置如下,入口处采用速度入口:ux=U∞=1.0,uy=0;出口处采用压力出口:p=0;上下边界均为自由滑移边界:∂ux/∂y=0,uy=0;圆柱表面均采用无滑移边界:ux=uy=0.为了获得较大的动力响应,不考虑结构阻尼的影响.对于弹性支撑圆柱体结构,可简化为质量-弹簧系统模型,圆柱表面速度为

图1 计算模型和边界条件Fig.1 Computational model and boundary conditions

2.2 网格划分

流场计算域采用非结构化三角形网格进行划分,其中圆柱附近及尾流区域进行网格加密处理.表1为不同网格参数下串列三圆柱结构涡激振动动力响应特性的统计结果对比.由表1 可知:与粗网格GI相比,网格GII 的Xmax/D与Ymax/D的计算结果最大变化率分别为5.26%和4.00%;与密网格GIII 相比,其最大变化率分别下降为1.25%和0.85%.网格GII已满足数值模拟结果网格收敛性要求和计算精度要求.综上所述,本文所有算例采用的网格密度和分布情况与GII 类似,无量纲计算时间步长Δt=0.002.

表1 网格独立性验证:串列布置三圆柱体流致振动计算结果(Re=100,r=1.0,Ur=6.0)Table 1 Grid independence test:The results for the three tandem circular cylinders at Re=100,r=1.0 and Ur=6.0

3 计算结果与分析

本文分析了不同雷诺数、固有频率比与约化速度工况下串列三圆柱体结构体系双自由度流致振动振幅特性、频谱特性、流体力系数的变化情况.本文根据UC 的振动特性对约化速度进行如下划分:3 ≤Ur≤5(区间A);5 ＜Ur≤9(区间B);9 ＜Ur≤15(区间C1),Ur＞15(区间C2).

3.1 振幅特性

由图2 可知,在区间A 内,UC 在x和y两个方向的振幅随约化速度的增大而增大.在大振幅区间内,频率比对UC 振幅的影响较大,具体表现为:当r≤1.5 时,频率比的变化对UC 的振动响应的影响较小.各工况下横流向振幅十分接近,在Ur=5 工况下达到最大振幅值后逐渐下降.频率比较小时结构刚度较大,圆柱顺流向振动响应微弱,x方向的振幅趋于0.当r=2.0,Ur=5 时,UC 横流向振动频率fs,y=0.174(Re=80,100)和0.178(Re=160)接近其固有频率,同时顺流向振动频率与固有频率的比值在1 附近.此时UC 发生双频共振,其振动响应显著增强,顺流向振幅远大于其他频率比工况下的振幅,横流向振幅也达到较大值.值得注意地是,当Re=80时,在双频共振作用下的尾涡模式为2S 模式,漩涡强度逐渐减弱并在下游不远处会消失,如图3(a)所示;Re=100 时的尾涡模式也呈2S 模式,但下游的漩涡重新卷起并脱落形成新的涡街;不同地是,Re=160时尾涡模式呈现P+S 模式,在较远的下游能保持较高的强度.雷诺数对UC 的振动响应的影响较小,各工况下UC 的振幅变化规律类似.进入C1区间后,UC 在x和y两个方向的振幅逐渐趋于稳定,x方向的振动响应极其微弱.

图2 不同雷诺数与频率比工况下,UC 在x 和y 两个方向最大振幅随约化速度的变化Fig.2 Variation of the maximum vibrating amplitudes of upstream cylinder with reduced velocity under different Reynolds number and frequency ratios

图3 Ur=5,r=2.0 时,流场瞬时涡量图Fig.3 Instantaneous vorticity diagram of flow field at Ur=5 and r=2.0

与UC 相比,雷诺数和频率比对MC 的振幅的影响更加显著.在区间A 内,MC 受到“弱锁定”作用,如图4 所示,Ur=4 时,x和y两个方向的振幅取得第一个极大值,当r=1.5 时顺流向振幅接近MC 的顺流向振幅最大值.特别地,当r=2.0 时,MC 在x和y两个方向的运动在区间A 内的振幅很小,这种“屏蔽”现象可以用流场进行解释.如图5 所示,当Ur=4时,UC 在靠近MC 的方向产生漩涡,而漩涡脱落的位置与UC 的距离非常近,连续涡结构的垂直距离较大,说明尾流发展过程中没有涡撞击的发生,漩涡直接从MC 和DC 的两侧通过,在UC 的下游不远处形成稳定的两列涡街.因此,MC 的漩涡脱落被显著抑制,进一步导致横向动力响应降低.在Ur=5 处,UC在P+S 尾涡模式中表现出较强的振动响应,涡结构的垂直距离被拉大,从而对振动产生实质性的抑制.Bao 等[29]也发现了类似的现象.在区间B 内,各工况下MC 的横流向运动在Ur=7 附近发生频率锁定现象,此时y方向的振幅最大,如图4 所示,且锁定区间的范围会随着雷诺数的增大而扩大.频率比对y方向的振幅影响较小,各工况下的振幅比较接近.特别的,当Re=160 时,在Ur=6 处的横流向振幅,r=2.0工况Ymax/D=0.322 远小于1.073 (r=1.0) 和1.025(r=1.5).频率比和雷诺数对x方向的振幅影响较大,Re＜160 时,x方向的振幅随频率比的增大而增大,特别的是,当Re=100,Ur=9 时,x方向的振幅与频率比成反比关系.当Re=160 时,r=1.0 工况下MC 在x方向上的振幅是其他频率比工况下振幅的2～3 倍,但在Ur=7 时Xmax/D=0.073 与其他工况下的振幅接近.在区间C 内(包括C1和C2),MC 逐渐退出锁定区间,圆柱振动响应逐渐减弱,因此MC在x和y方向的振幅逐渐减小并趋于稳定.值得注意的是,当r=1.0 时,在C1区间内各雷诺数工况下MC 在x方向上的振动仍会保持相当大的振幅,达到该工况下顺流向振幅的最大值后逐渐下降趋于平稳.总的来说,MC 的动力响应受UC 尾流振荡的影响较大,相反,频率比的影响较小.

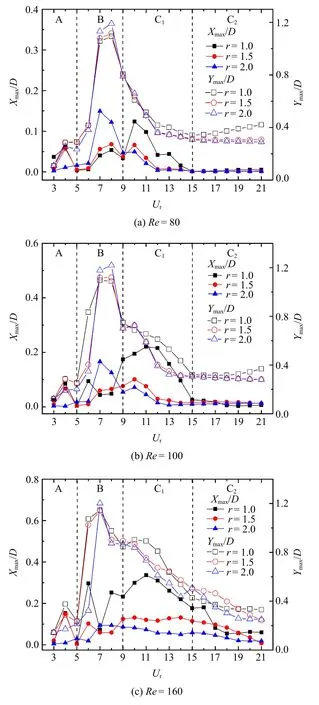
图4 不同雷诺数与频率比工况下,MC 在x 和y 两个方向最大振幅随约化速度的变化Fig.4 Variation of the maximum vibrating amplitudes of midstream cylinder with reduced velocity under different Reynolds numbers and frequency ratios

图5 Re=160,r=2.0 时,流场瞬时涡量图Fig.5 Instantaneous vorticity diagram of flow field at Re=160 and r=2.0

DC 振幅的变化趋势与MC 类似,但DC 的“锁定”区间的范围比MC 更宽,且会随着雷诺数的增大而明显扩大.在区间A 内DC 在x和y两个方向的振幅较小,Ur=4 时出现与MC 类似的“弱锁定”现象,此时振幅出现小幅度的“上升-下降”过程,如图6 所示.特别的是,当r=2.0 工况DC 在区间A 内的振幅波动很小.由于UC 和MC 尾流的共同“屏蔽”作用,当Ur≤6 时,各工况下DC 的两个方向的振幅均小于UC 和MC 的振幅;但当Ur＞6 时,DC 在两个方向的振幅均大于UC 和MC 的振幅.由此可见,本文的临界约化速度在6～7 之间,且受雷诺数与频率比的影响较小[16,30].在区间B 内,DC 在y方向上突然剧烈振动,随Ur增大,横流向振幅取得最大值后下降,但仍保持较大的振幅值.但Re=160 时,在整个B 区间内横流向振幅均不断增大.值得注意的是,与其他频率比工况相比,r=2.0 时DC 进入大振幅区间的约化速度Ur=7.在区间C1内,随着Ur的增大,不同雷诺数和频率比工况下DC 的横流向振幅在取得最大值后逐渐减小.当Re=160 时,r=1.5 与其他工况完全不同,此时横流向振幅在整个区间C1内均保持较大的数值.值得注意地是,当r=2.0 时,横流向振幅在Ur=14 处突然减小,Ymax/D=0.849(r=2.0)约为r=1.5 工况的53%(Ymax/D=1.583).在区间C 内DC顺流向振幅受频率比的影响比横流向振幅更敏感,具体地说:当r=1.0 时,随着Ur的增大,DC 的顺流向运动在Ur=11 附近达到该工况下的最大振幅值后逐渐下降,此时DC 在C1区间内的顺流向振幅远大于其他频率比工况下的振幅.当r＞1 时,不同雷诺数下DC 顺流向运动在区间C1内较弱,振幅较小且呈现逐渐下降的趋势.特殊的是,当Re=160,r=1.5时,DC 顺流向振幅在Ur＞12 后出现明显的跃升,并达到该工况下顺流向振幅最大值Xmax/D=1.12.C2区间内DC 在两个方向的振幅进一步减小,逐渐趋于稳定.值得注意地是,当Re＜160,r=1.0 时,DC 的横流向振幅在C2区间内出现增大的趋势.同时,MC也具有相同的变化规律.

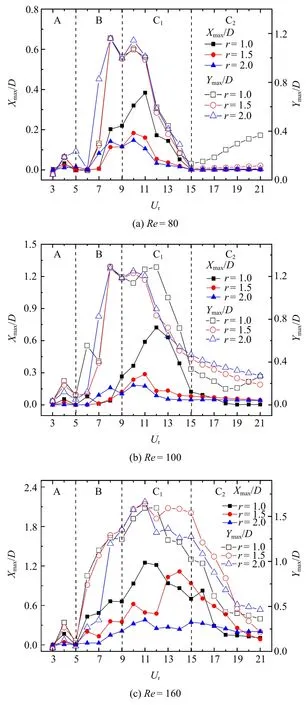
图6 不同雷诺数与频率比工况下,DC 在x 和y 两个方向最大振幅随约化速度的变化Fig.6 Variation of the maximum vibrating amplitudes of downstream cylinder with reduced velocity under different Reynolds numbers and frequency ratios

3.2 流体力系数分析

Lx=5.5D工况下,MC 对UC 的影响极其微小,UC 的尾流能够得到充分发展,导致其振动响应类似于单圆柱工况[18].另一方面,受到UC 尾流和自身涡脱落的共同作用,使得MC 和DC 振动响应发生显著变化[15].

由图7(a) 可知,随约化速度的增大,UC 在各工况下阻力系数的平均值(CD-mean)逐渐增大,频率比对CD-mean 的影响很小,雷诺数越大CD-mean 越大.特别的,在r=2.0 工况下,当Re=160,Ur=4 时CD-mean=2.405 远大于其他雷诺数工况,此时UC 顺流向振幅Xmax/D=0.192 3 分别是0.015 8 (Re=80)和0.022 9(Re=100)的12 倍和8 倍.UC 的CD-mean在Ur=5 处达到最大值随后逐渐降低并最终保持稳定,CD-mean 随频率比的增大而增大,但与雷诺数成反比.区间A 内MC 受UC 尾流的屏蔽作用,MC的CD-mean 幅值较小且小幅下降,此时频率比小的工况下CD-mean 反而较大.随着MC 进入大振幅区间,CD-mean 显著增大并在Ur=7 时达到最大值并逐渐减小趋于稳定,此时CD-mean 受频率比的影响很小.值得注意地是,MC 的CD-mean 稳定时的幅值大约是UC 的一半.DC 的CD-mean 随约化速度的变化十分复杂,同时雷诺数与频率比对CD-mean 的影响也较为显著.CD-mean 在区间A 和区间B 内的波动较大,分别在Ur=4 和Ur=8 时达到两个极值.在区间C 内,雷诺数越大DC 的CD-mean 越大,随Ur增大,CD-mean 逐渐减小并趋于稳定.

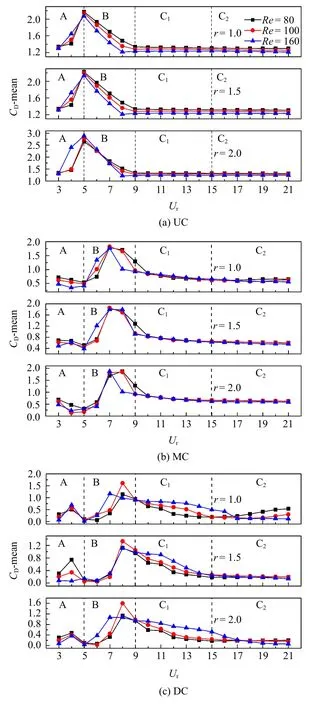
图7 不同雷诺数工况下,圆柱阻力系数平均值的变化Fig.7 Variation of mean value of drag coefficient under different Reynolds numbers

UC 在各工况下升力系数的均方根值(CL-rms)随约化速度的变化趋势与CD-mean 变化类似,从图8(a)可以看出,各工况下UC 的CL-rms 大致呈现先增大后降低直到平稳的变化趋势,并在Ur=4 处达到最大值.随雷诺数的增大,UC 的CL-rms 变大,此时在y方向的振动响应变化剧烈程度变强.但当r≤1.5,Ur=5 时,雷诺数与UC 的CL-rms 却成反比.MC 的CL-rms 在Ur=3 处就达到最大值,随着Ur增大,CL-rms 迅速减小,频率比和雷诺数对CL-rms的影响很小.在区间B 内,MC 的CL-rms 曲线变化的波动性明显增强.当Re=160 时,不同频率比工况下CL-rms 曲线出现多个突变点.值得注意地是,当Ur=6 时,MC 在r=2.0 工况下的CL-rms=0.081 远小于0.565(r=1.0)和0.577(r=1.5),导致此MC 的在y方向的振幅远小于其他频率比工况下的振幅.在区间C 内,CL-rms 变化很小呈平稳趋势.“弱锁定”作用使DC 的CL-rms 在Ur=4 处突然增大,随后逐渐减小.当5 ＜Ur＜15 时,雷诺数和频率比对DC 的CL-rms 的影响很强,DC 的CL-rms 曲线出现很强的波动.特别的,在Re=160 工况下,当r=1.5,Ur=15时,MC 脱落的漩涡会与DC 上、下侧的剪切层融合形成更强的漩涡,加剧DC 的振动响应,导致其升力系数的波动性会增强,如图9 所示.i 时刻,DC 处于上方最大位移处,其尾流上方的漩涡基本已脱离,同时MC 尾流已传播至其下方,使得DC 下表面受到较大吸力.在ii 时刻,DC 的尾流区会出现一个大漩涡,同时迎流面会受到MC 尾流的冲击作用.随后,DC 运动至下方最大位移处,其尾流上方的漩涡与MC 尾流已融合成一个整体,使得DC 上表面受到较大吸力.

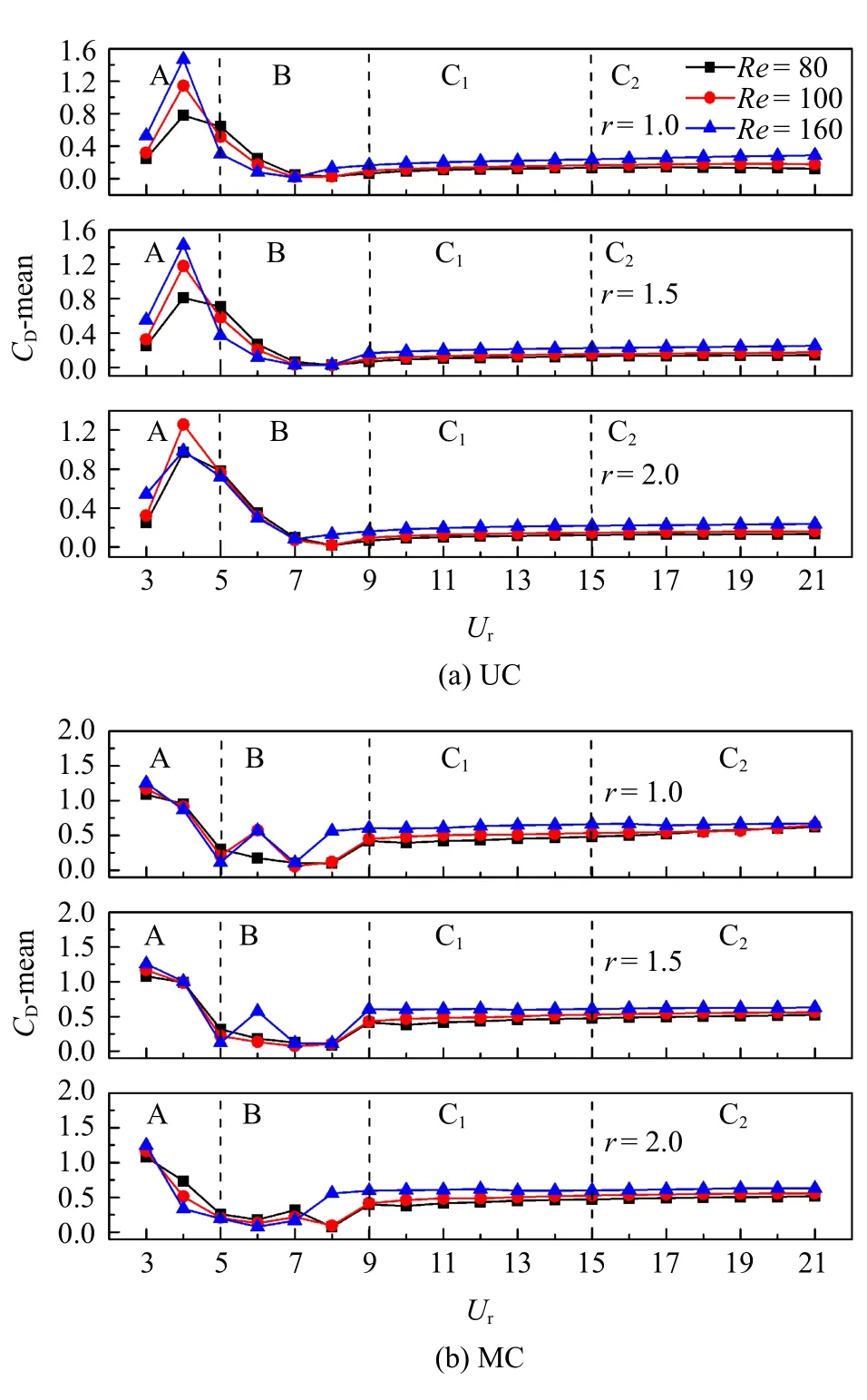
图8 不同雷诺数工况下,圆柱升力系数均方根值的变化Fig.8 Variation of root mean square value of lift coefficient under different Reynolds numbers

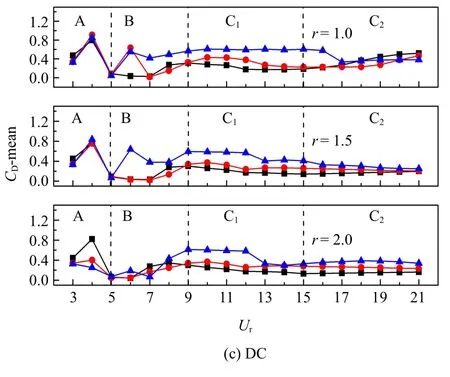
图8 不同雷诺数工况下,圆柱升力系数均方根值的变化(续)Fig.8 Variation of root mean square value of lift coefficient under different Reynolds numbers(continued)

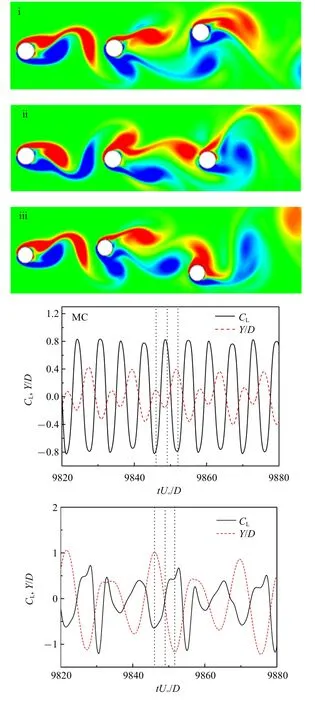
图9 Re=160,r=1.5,Ur=15 时,DC 运动位移及升力时程曲线图及对应不同时刻涡量场云图Fig.9 Time-history curve of displacement and lift coefficient of downstream cylinders and instantaneous pressure contours at different times when Re=160,r=1.5 and Ur=15

3.3 流体力功率谱密度分析

通过对圆柱体流体力系数功率谱密度(PSD)对比分析,发现圆柱流体力系数PSD 曲线在不同雷诺数工况下呈现不同的主峰幅值、频谱成分及波动性,导致圆柱动力响应特性发生较大变化.另外,研究发现r与Ur的变化对PSD 曲线有显著影响,导致圆柱动力学响应呈现明显的差异性.本节针对r=1.0 和2.0 工况下三圆柱体流体力系数PSD 曲线的变化及其对圆柱的振动响应的影响进行详细分析.

在区间A 内,当r=1.0 且Ur=3 时,各工况下UC 的流体力系数PSD 曲线出现两阶频率峰值且曲线均比较光滑,随着约化速度和雷诺数的增大,PSD曲线的波动性增强,如图10(a) 所示,在一阶频率聚集了更多的能量,增强了UC 的振动响应.Ur增大到5 时,各雷诺数工况下升力系数PSD 曲线波动性减弱,曲线包含的频率峰值增大至三阶,有效增大了升力系数PSD 曲线包围的面积,使得UC 获得更多动能,在y方向上产生较大的振幅,具体分析见第3.4节.在区间B 内,随Ur增大,升力系数PSD 曲线波动性增强,但阻力系数PSD 曲线受约化速度的影响较小.各工况下升力系数PSD 曲线包含了主峰幅值与次峰幅值同等量级的多阶频率峰值,此时能量在次峰的分布比Ur=5 工况更加丰富,而主频能量值更低,流体流向结构的能量值减少,导致UC 的振动响应比Ur=5 时有所减弱.随Ur进一步增大,升、阻力系数PSD 曲线趋于光滑,频率峰值逐渐减少至二阶,主峰幅值逐渐稳定,次峰幅值逐渐减小直至可以忽略,UC 在区间C 内的振动响应逐渐减弱,在两个方向的振幅趋于稳定,最终PSD 曲线逐渐形成光滑的双峰谱形态.

图10 不同工况下,上游圆柱升力系数功率谱密度(红线)与阻力系数功率谱密度(黑线)Fig.10 PSD of lift coefficient(red)and drag coefficient(black)of upstream cylinder under different case

当r增大至2.0 时,在区间A 内,如图10(e) 和图10(f)所示,各工况下流体力系数PSD 曲线的波动性很弱,随着约化速度和雷诺数的增大,PSD 曲线的频率峰值成分增大,UC 的运动变得复杂,其他特征与r=1.0 时类似.在区间B 内,各工况下圆柱流体力PSD 曲线均只出现三阶频率峰值,在Ur＞7 后,PSD曲线的波动性逐渐减弱,主导频率的能量值越来越低,UC 的动力学响应也越来越弱,即圆柱振动响应的强弱与主频能量值成正比.需要说明的是,Ur=8时,雷诺数对升力系数PSD 曲线有显著的影响.当Re=160 时,升力系数PSD 曲线波动性与其他工况相比明显增强,次峰及杂频占据的能量值增多,此时各工况下升力系数PSD 曲线的主频能量值几乎相同.升力系数PSD 曲线的波动性对UC 运动的产生较大影响,Re=160 时UC 横流向振幅Ymax/D=0.131 相较于Re=100 时的Ymax/D=0.366 下降了64%,同时比Ur=7 时的Ymax/D=0.705 下降了81%.研究发现,当r=1.0 时同样具有类似规律.进入区间C后,PSD 曲线随约化速度的增大而变得光滑,雷诺数越小曲线的波动也越来越弱,最终形成光滑的两阶频率峰值形态.

与UC 相比,MC 由于受到上游圆柱的尾流影响,流体力系数PSD 曲线随雷诺数和约化速度的变化更加复杂.当r=1.0 时,在区间A 内,不同工况下的升、阻力系数PSD 曲线均比较光滑,分别包含三阶和两阶频率峰值,但主频能量值较小,圆柱振动响微弱.特别地,当Ur=4 时,PSD 曲线的波动性随雷诺数的增大而增强,如图11(a)～图11(c) 所示,PSD 曲线出现多阶同等量级的频率峰值,表明此时的泄涡频率不位于锁定区间.在区间B 内,当Re＜160,升力系数PSD 曲线的频率峰值数量随Ur的增大而增大,圆柱运动趋于复杂.Re=160 时,升力系数PSD 曲线波动性增强,并包含多阶频率峰值,主频维持较高能量值,故此时MC 在y方向的运动能以较大的振幅持续到区间B 的末端.随着Ur增大,阻力系数PSD 曲线变化较小,仅表现为波动性的差异,所以在区间B内顺流向振动相对平稳,振幅较区间A 有小幅度增大.特别地,当Re=160 时,如图11(c)所示,Ur=6 时阻力系数PSD 曲线主、次频峰值的能量值接近,且能量在各杂频的分布幅值也较多,圆柱顺流向振动响应较强.随着Ur增大,阻力系数PSD 曲线的频率幅值减少到三阶(Ur=7),主频能量值与Ur=6 工况相比差了一个数量级,顺流向振幅Xmax/D=0.073 与Ur=6 工况比降低了三倍.流体力系数的PSD 曲线在区间C 后波动逐渐减弱,并逐渐形成光滑的三阶频率峰值曲线.

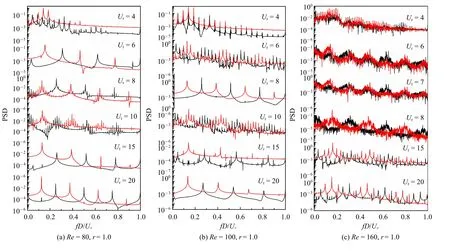
图11 不同工况下,中游圆柱升力系数功率谱密度(红线)与阻力系数功率谱密度(黑线)Fig.11 PSD of lift coefficient(red)and drag coefficient(black)of midstream cylinder under different cases

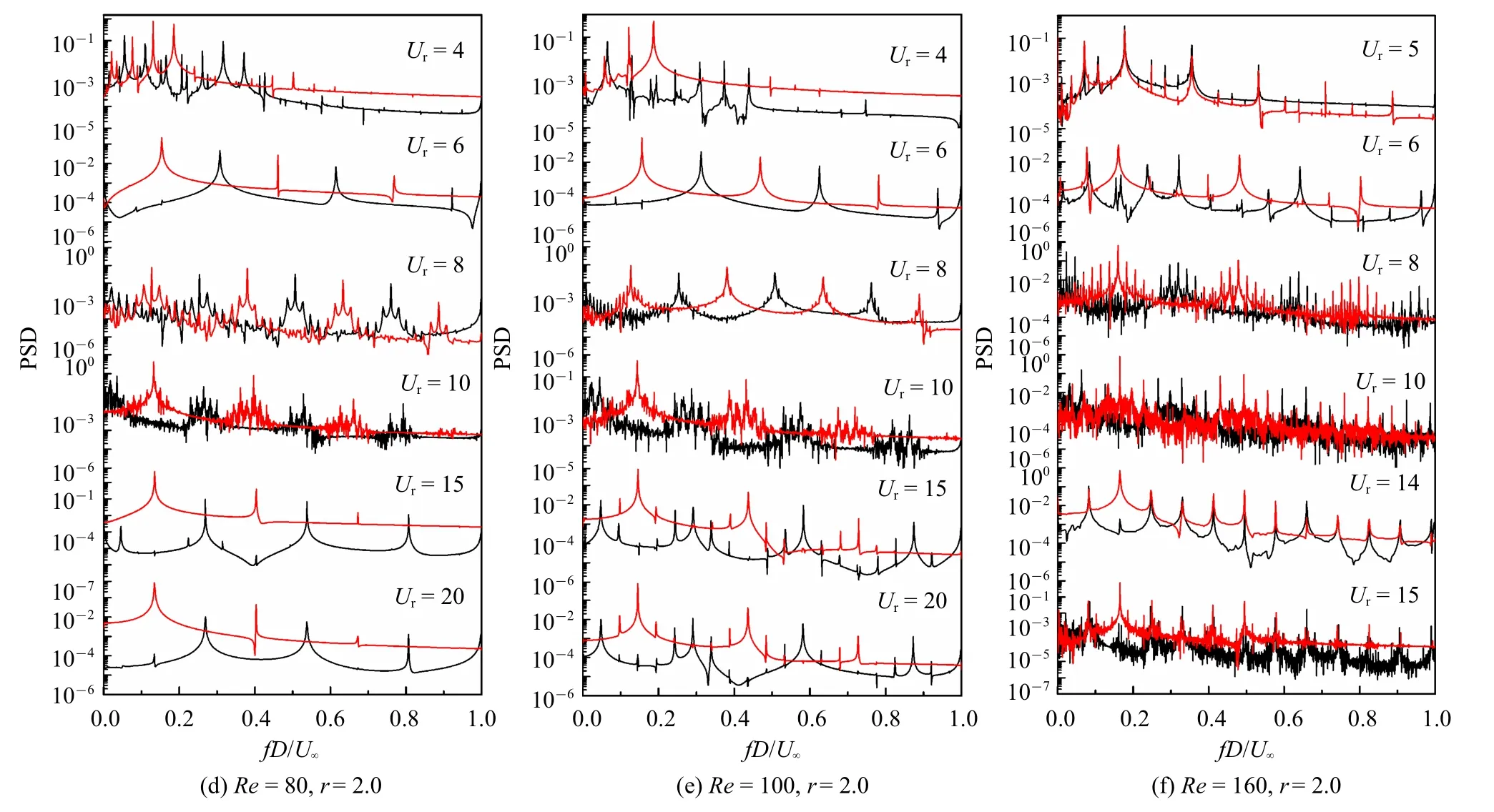
图11 不同工况下,中游圆柱升力系数功率谱密度(红线)与阻力系数功率谱密度(黑线)(续)Fig.11 PSD of lift coefficient(red)and drag coefficient(black)of midstream cylinder under different cases(continued)

当r=2.0 时,在区间A 内PSD 曲线的波动性随雷诺数的增大而减弱,如图11(f)所示,Ur=4 时MC的“弱锁定”作用逐渐消失,流体经过MC 时传递给圆柱的能量减少,导致圆柱的动力学响应十分微弱.当Ur=5 时,雷诺数对升、阻力系数PSD 的影响十分显著.当Re=100 时,阻力系数PSD 的主峰值频率fscd=0.352 是升力系数PSD 的两倍,从UC 脱落的漩涡直接从MC 上、下侧通过,如图12 所示,导致MC 的运动轨迹呈现为对称的“8”字型,与Prasanth等[31]研究的结论一致.但当Re=160 时,升、阻力系数PSD 曲线的各阶峰值频率完全重叠,UC 在一个周期内脱落的孤立漩涡A 和一对反向的漩涡B+C,分别从MC 的上、下侧向下游发展,由于上下侧涡量不对称,导致MC 的运动轨迹由“8”字形变成不对称形状.值得注意地是,上述工况下MC 受到UC 的“屏蔽”作用较大,且此时升、阻力曲线与位移的时程曲线的几乎反向,导致MC 在Ur=5 时的振动响应很弱.在区间B 内,MC 进入锁定区间,当Ur接近8 时,PSD 曲线中会出现高阶的频率峰值,曲线波动性也大大减弱.此时MC 被完全锁定,更多的能量由流体传递给圆柱,MC 获得更多的动能而剧烈振动,x和y方向的振幅达到最大值.进入区间C 后,Re＜160 时升力系数的PSD 曲线的变化规律与r=1.0 时大体相同.但当Re=160 时,在C1区间内,升力系数PSD曲线中出现了多阶频率峰值,包含的总能量值高,使得MC 产生较大的横流向振幅.在C2区间中,升、阻力系数PSD 曲线波动性逐渐减弱,逐渐形成光滑的三阶频率峰值曲线.

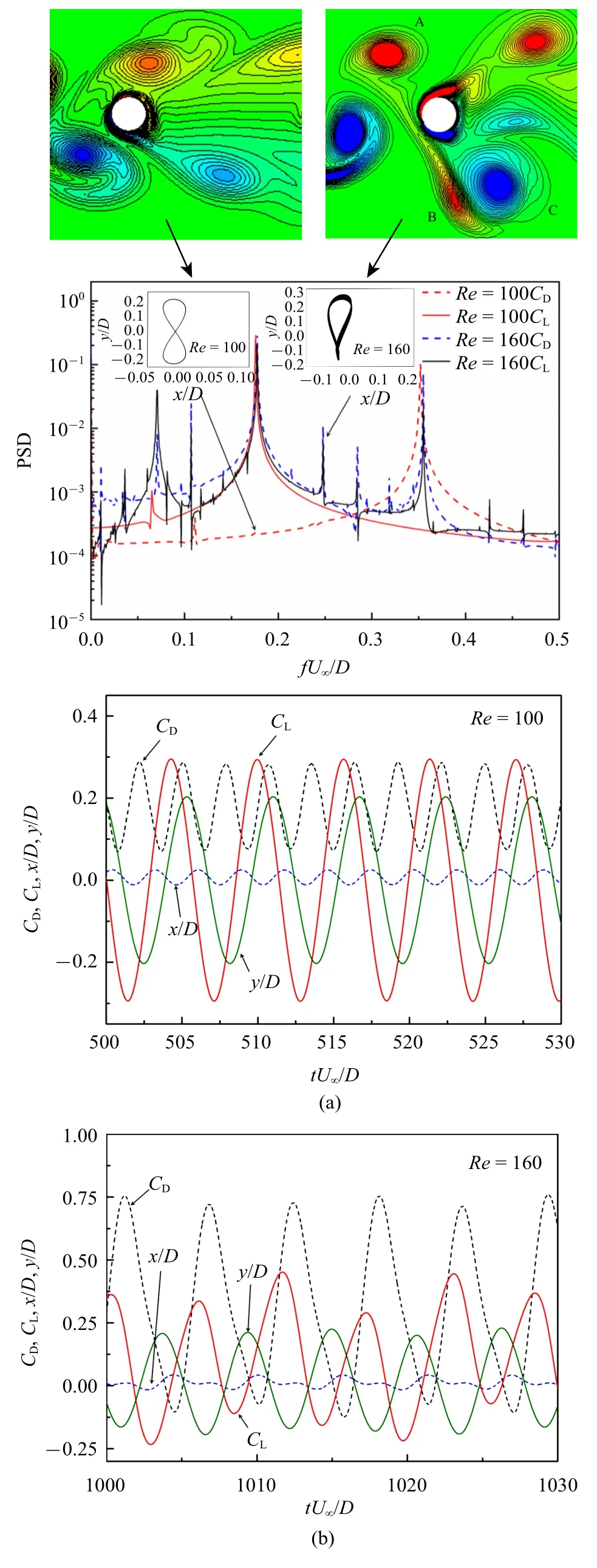
图12 Re=100 与160 时中游圆柱流体力系数与位移时程曲线、运动轨迹及流场图(r=2.0,Ur=5)Fig.12 Time history of the fluid force coefficient and displacement,the trajectory and the flow field of midstream cylinder at Re=100 and 160(r=2.0,Ur=5)

DC 受到上中游两圆柱的尾流共同作用,雷诺数、频率比和约化速度对升、阻力系数PSD 的影响更加显著.当r=1.0 时,与MC 类似,PSD 曲线在Ur=4 时出现数量众多的频率峰值,主频能量值较高,PSD 曲线的波动性随雷诺数的增大而增强,如图13(a)～图13(c)所示,导致DC 在A 区间内的运动在Ur=4 时最强烈.在区间B 内,随Ur增大PSD 曲线中出现了更多数量的的频率峰值,同时曲线的波动性也明显增强,导致DC 的运动越趋复杂.特殊地,当Re=100,Ur=7 时,升力系数PSD 曲线的频率峰值比Ur=6 工况时更多,主频能量值却少了两个数量级,致使DC 的横流向振幅减小.当Ur=8 时,雷诺数对PSD 曲线影响十分显著,当Re=100 时,如图13(a)～图13(c)所示,升力系数PSD 曲线光滑且中出现四阶频率峰值.当Re=160 时,升力系数PSD 曲线由繁多的峰值构成整体呈下降趋势的曲线.研究发现,上述的3 种不同的曲线形态是串列布置三圆柱体的PSD 曲线的最基本形态.C 区间内,升力系数PSD曲线中出现多阶频率峰值,包含较高的能量值,导致下游圆柱产生强烈的动力学响应.当Ur＞13,PSD 曲线的波动性逐渐增强,杂频占据的能量值增大,圆柱体获取的能量值减少,导致下游圆柱的横流向振幅逐渐减小.与UC 和MC 不同,当Re=80 时,在Ur＞15后,升力系数PSD 曲线中出现三阶频率峰值,主频能量值随Ur增大而变大,使得DC 横流向振幅不断增大.随Ur增大,阻力系数PSD 曲线的主频能量值逐渐降低,导致DC 顺流向振幅减小.当r=2.0 时,升力系数PSD 曲线随约化速度的变化规律与r=1.0工况基本一致,如图13(d)和图13(f)所示,仅在频率峰值数量及主频能量值有细微差距.由此可见,流体力系数PSD 曲线随约化速度的变化规律:Ur较小时PSD 曲线光滑,随Ur增大PSD 曲线波动性增强,最终PSD 曲线逐渐光滑,与圆柱的运动轨迹的变化规律类似.

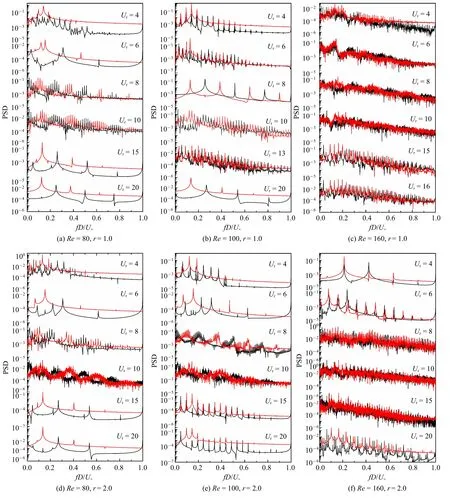
图13 不同工况下,下游圆柱升力系数功率谱密度(红线)与阻力系数功率谱密度(黑线)Fig.13 PSD of lift coefficient(red)and drag coefficient(black)of downstream cylinder under different cases

3.4 结构频谱机理分析

结构功率谱密度能反映单位频带内激励荷载功率随频率的分布,可以得到各个峰值频率成分的幅值,从而衡量不同峰值频率对结构响应的贡献,是结构频谱分析的重要手段,涡激振动中激励荷载包括流体力、位移等[32].通过结构功率谱密度分析,可以判断激励荷载信号响应的强弱,从而对结构动力学响应进行分析.圆柱的横流向位移与升力系数功率谱密度曲线包围的面积Ay和Acl分别代表位移与升力系数的平均功率值.本节以Re=100,r=1.0 工况为例,对结构功率谱密度曲线和激励荷载平均功率值与结构振动的关系进行分析.

由图14(a)可知,圆柱顺流向位移平均功率值Ay随约化速度的变化趋势与其在y方向的振幅变化趋势类似.当Ur=5 时,上游圆柱位移PSD 曲线出现fsy与3fsy二阶频率峰值,如图15(a)所示,其主频能量值较Ur=3 时更大,增大了位移平均功率值,激励UC 发生大振幅振动.另一方面,此时涡脱落频率fsy=0.18 与圆柱的固有频率(fn,y=0.20)接近,UC 发生横流向锁定现象,产生较大振幅.当Ur=5 和8 时,UC 的PSD 曲线表现为光滑的多峰谱特征,其运动轨迹表现为规则的“8”字形;但Ur=9 时,PSD 曲线的波动性增强并在主频附近出现许多锯齿形的窄带峰值,削弱了主频能量值,导致UC 运动的不规则性及随机性增强,诱发产生小振幅顺流向运动,如图15(a)所示.进一步研究发现,在某约化速度区间内,圆柱横流向振幅Ymax/D与位移信号平均功率值Ay的大小成正比.

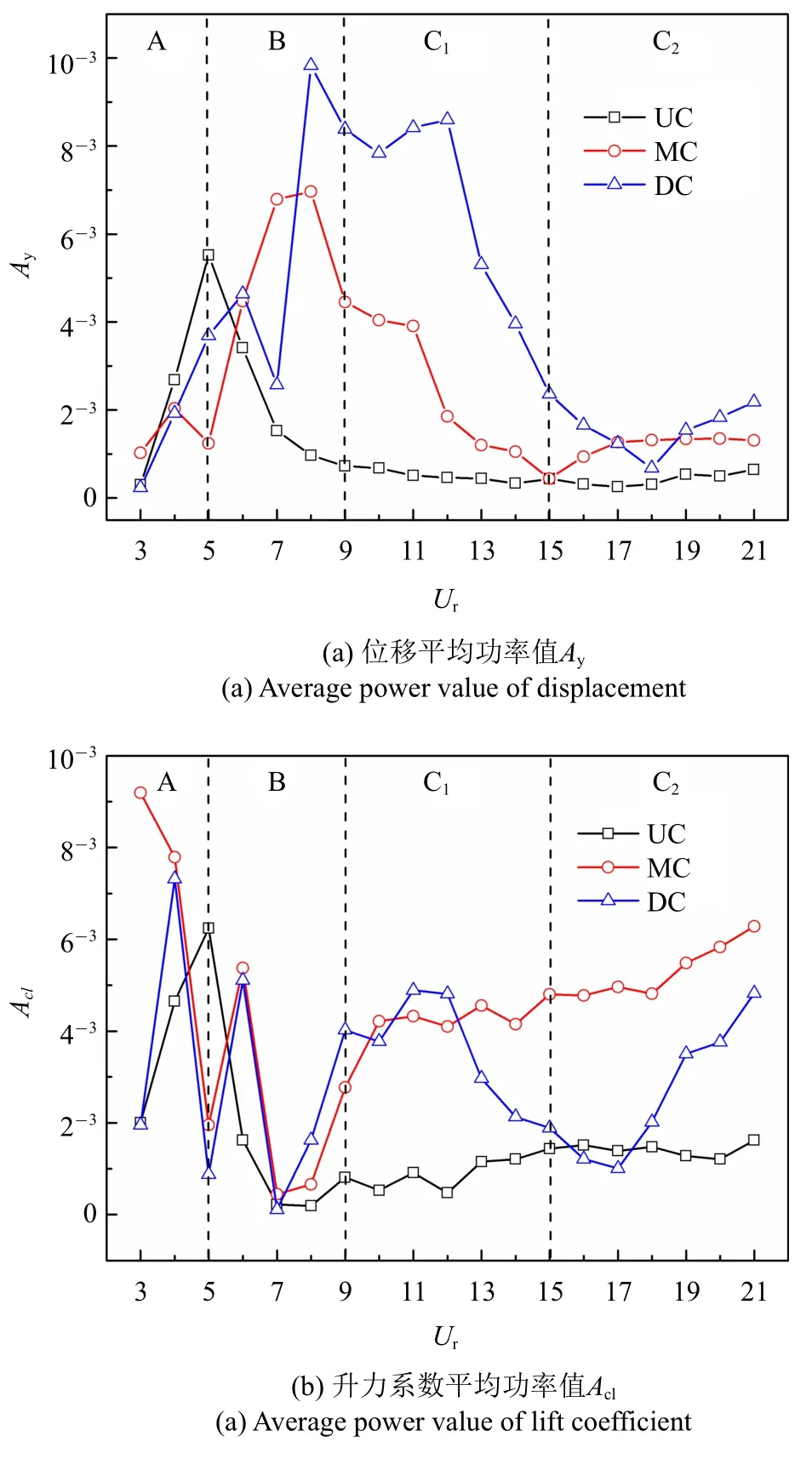
图14 Re=100,r=1.0 工况下圆柱位移与升力系数平均功率值随约化速度的变化Fig.14 Variation of average power value of cylinder displacement and lift coefficient with reduced velocity at Re=100 and r=1.0

通过对比发现,在区间A 和B 内,升力系数平均功率值随Ur的变化规律与升力系数均方根值的变化规律类似,且圆柱升力系数均方根值随升力平均功率值Acl的增大而增大.与Ur=3 工况相比,如图15(b)所示,当Ur=5 时,UC 的升力系数PSD 曲线的频谱成分更丰富,出现fscl,3fscl与5fscl三阶频率峰值,UC 的升力系数平均功率值增大,进而增强了UC 的振动响应.Ur=9 工况下PSD 曲线的窄带峰值数量明显增多,且分布的频带更宽.在区间C 内,升力系数均方根值变化的波动加强,但维持了升力系数均方根值的变化趋势.

图15 Re=100 与r=1.0 时,上游圆柱功率谱密度Fig.15 PSD of upstream cylinder at Re=100 and r=1.0

需要注意的是,对不同约化速度区间的工况进行频谱分析时,必须优先考虑振动频率比(fs/fn,y)的影响.当Ur=8 时,UC 升力系数平均功率值比Ur=3 工况更小,而此时UC 的Ymax/D达到0.271是Ur=3 工况下的近9 倍.这是由于Ur=8 时的主频fscl=0.128 接近固有频率fn,y=0.125,UC 发生横流向共振并产生较大振幅.由此可见,对升力系数功率谱密度分析时,振动频率比与激励荷载平均功率值是影响结构振动响应强弱的两个重要参数.

4 结论

基于四步半隐式特征线分裂算子有限元方法,对串列布置三圆柱双自由度结构体系涡激振动问题进行了数值模拟,分析了雷诺数、频率比和约化速度的变化对结构振动响应及频谱特性的影响,主要结论如下:

(1)UC 两个方向的振幅均比较小,雷诺数、频率比对振幅的影响较小.MC 的锁定区间的范围随着雷诺数的增大而扩大,其动力响应受频率比的影响很小.本文的临界约化速度在6.0 附近,且受雷诺数的影响较小.DC 的顺流向振幅受频率比和雷诺数的影响更为显著.

(2)UC 的CD-mean 与CL-rms 随约化速度的变化出现先增大后降低直至平稳的趋势,受雷诺数和频率比影响较小.由于MC 受到UC 尾流的影响,导致其CL-rms 与CD-mean 与UC 完全不同,约化速度较小时受雷诺数和频率比的影响较大.DC 的CL-rms 受雷诺数和频率比的影响十分显著.中下游圆柱CD-mean的变化趋势与UC 类似.

(3) 圆柱流体力系数PSD 曲线的波动性随雷诺数和频率比的增大而增强,主峰能量值越大圆柱振动响应越积极,PSD 曲线波动性越大,圆柱运动轨迹越不规则.当升、阻力系数PSD 曲线的主峰重叠时,圆柱沿着非对称轨迹运动.约化速度较小时PSD 曲线光滑,在大振幅区间内PSD 曲线波动性增强且频谱成分增多,最终PSD 曲线趋于光滑.

(4)激励荷载平均功率值随Ur的变化趋势与对应的结构动力响应的变化类似.在同一约化速度区间内,结构振动响应的强弱与位移的平均功率值成正比.对升力系数功率谱密度分析时,区间A 和B 内升力系数均方根值与升力平均功率值成正比.在其他区间振动频率比对结构振动响应的影响更大.