基于AS 5100.2标准的铁路桥梁垂向活载校核计算研究及应用
2021-11-09杨诗卫付茂海张瑞国邹梦竹
杨诗卫,付茂海,黄 盼,张瑞国,李 冬,淑 梅,彭 燎,邹梦竹
(1.中车眉山车辆有限公司 产品开发部,四川 眉山620020;2.西南交通大学 机械工程学院,四川 成都 610031 )
据不完全统计,截至目前,我国出口澳大利亚的各型铁路货车数量已接近3万辆,澳大利亚已成为我国铁路货车出口的重要目标市场。随着“一带一路”倡议的不断推进,将会有更多的新型铁路货车出口澳大利亚。部分澳大利亚用户要求在新车辆的设计认证阶段提供所设计车辆的桥梁载荷效应评估报告,供澳方铁路管理部门审查、备案。由于需要校核的桥梁跨距多、载荷组合复杂,人工计算非常困难、繁琐,且耗时长,目前国内主要铁路货车出口企业向澳大利亚提供的报告基本委托澳大利亚咨询公司完成,咨询费用不菲,且周期较长。为便于设计人员在客户询价阶段或项目投标阶段快速选择车辆长度、定距和邻轴距等关键技术参数,及时回应用户,并在项目设计方案认证阶段准确撰写认证所需桥梁车辆载荷效应评估(以下简称“车辆评估”)报告,研究澳大利亚标准桥梁垂向活载校核计算方法以及开发相应的计算软件具有重要的工程实用价值。
我国对铁路桥梁活载标准的运用进行了较多研究,但均未给出活载作用下桥梁所受最大剪力和弯矩的计算方法。文献[1]中基于修正后中-活载(2005)的ZH图式,从静活载储备、考虑恒载和相关设计参数的储备两方面对重载列车作用下桥梁结构设计荷载系数的取值进行了研究,提出了适用于新建重载铁路设计的荷载系数;文献[2]回顾了我国铁路列车荷载图式的研究和发展情况,介绍了各种类型荷载图式的适用范围和应用中需注意的问题,提出了进一步开展配套竖向动力系数、横向摇摆力和离心力、纵向牵引力和制动力的研究建议;文献[3]基于对目前世界各国高速铁路上运行的典型车辆及其采用的活载标准的研究,针对我国高速铁路桥梁常见的结构形式,对常用的中小跨距简支梁、连续梁在现行运营车辆荷载和多种标准设计活载下的结构响应进行了比较分析,得出了我国的中小跨距高速铁路桥梁结构设计安全储备量过大的结论,建议采用0.6UIC活载作为高速铁路客运专线中小跨距桥梁设计活载,采用UIC活载作为高速铁路客货共线中小跨距桥梁的设计活载;文献[4]对我国列车目前实际开行长度、未来开行长度和开行时间间隔进行了研究,分析了加载长度对大跨距桥梁的影响,给出了超大跨距铁路桥梁列车加载长度。
本文通过分析AS 5100.2:2017《桥梁设计: 第2部分:设计载荷》中300LA活载和车辆评估时轴载荷的组合工况,提出最大静态剪力和弯矩的计算方法,并推导出相关计算公式,采用Visual Basic语言编写校核计算程序,运用该程序计算跨距为1~100 m的桥梁在300LA活载作用下的最大静态剪力和弯矩,并将计算结果与AS 5100.2:2017中对应值进行比较,以验证所述计算方法的正确性和程序计算精度,为设计人员提供快速选择车辆长度、车辆定距、邻轴距等关键技术参数和撰写桥梁车辆载荷效应评估报告的工具。
1 澳大利亚铁路桥梁活载等级及评估准则
澳大利亚现行的铁路桥梁活载基准等级为AS 5100.2:2017中规定的300LA,活载300LA图式如图1所示。300LA由若干轴重为300 kN的车辆车轴组成的车轴组和1根轴重为360 kN的机车车轴构成,车轴组内各轴距离依次为1 700 mm、1 100 mm和1 700 mm,车轴组间距离为12 000~20 000 mm,机车车轴与相邻车轴的中心距离为2 000 mm。车轴组数量根据所评估桥梁跨距需求确定。
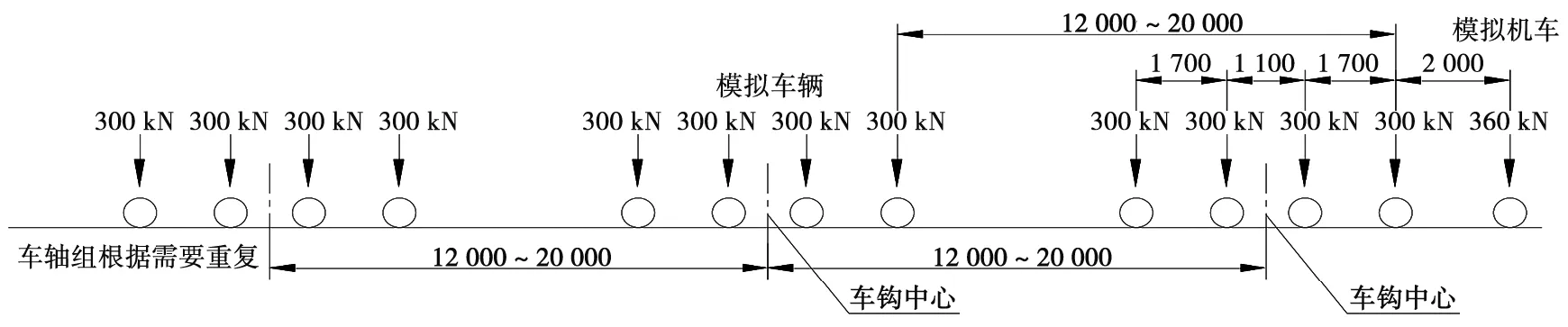
图1 活载300LA图式
除基准活载300LA外,澳大利亚还有其他等级的活载,活载等级仍采用数字和英文字母“LA”的组合表示(如180LA、230LA)。其他活载图式中,各轴轴距与基准活载300LA的轴距相同,车辆轴轴重与表示等级的数字相等,机车轴轴重由基准活载机车轴的轴重(360 kN)乘以换算系数而得,换算系数为该等级的车辆轴轴重与基准活载车辆轴轴重(300 kN)的比值。例如:活载等级230LA中,车辆轴轴重为230 kN,机车轴轴重为360×230/300=276 (kN)。
根据AS 5100.2:2017要求,新设计车辆的桥梁载荷效应评估(以下简称车辆评估)需以1 m为间隔,分别计算由新设计车辆组成的满载列车通过跨距为1~136 m的桥梁时作用于桥梁的最大静态剪力和弯矩,计算所得各值不得大于用户指定标准活载作用下对应跨距的最大静态剪力和弯矩。
2 计算模型
2.1 载荷工况
车辆评估时,需将跨距为1~136 m的桥梁在由新设计车辆组成的满载列车作用下所受的最大静态剪力和弯矩与标准活载下各对应值进行比较,但AS 5100.2:2017附录C的表C2中仅列出了在300LA活载下跨距为1~100 m桥梁的最大静态剪力和弯矩,需使用者自行补充计算跨距为101~136 m的桥梁在300LA活载作用下所受的最大静态剪力和弯矩。因此,评估用的计算程序应既适用于标准活载作用下的剪力和弯矩计算,又适用于车辆评估的剪力和弯矩计算。
载荷组合状态及载荷间距将影响载荷效应,相同跨距的桥梁在不同组合及不同间距的载荷作用下将承受不同的剪力和弯矩,因此计算剪力和弯矩前需对300LA活载和车辆评估的载荷组合工况进行分析。
图2为300LA活载效应计算和车辆评估时各轴几何关系。图2中,将300LA活载效应计算和车辆评估的轴载荷序号从右到左依次记为1号、2号、3号……n号,机车轴载荷记为F1,车辆轴载荷记为F2,l代表桥梁跨距。将2号轴与1号轴的轴间距记为d2,3号轴与1号轴的轴间距记为d3,依次类推,n号轴与1号轴间距离记为dn;2号轴与3号轴的轴间距记为b1,2号轴与4号轴的轴间距记为b2,2号轴与5号轴的的轴间距记为b3,2号轴与6号轴的轴间距记为b4,从6号轴与7号轴的轴间距开始,其余相邻两轴的轴间距将以间隔4根轴为周期循环出现b1、b2、b3和b4。
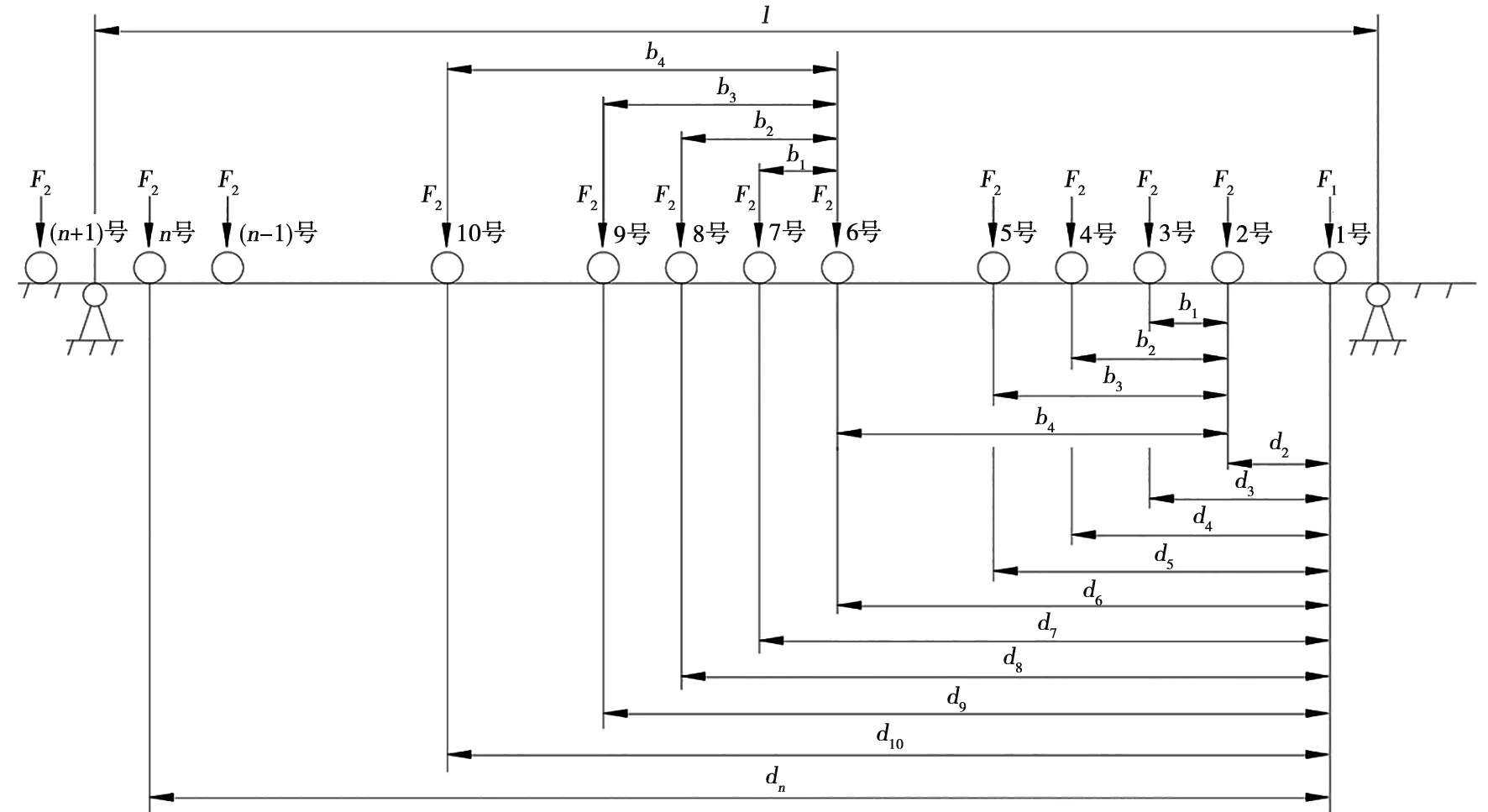
图2 300LA活载效应计算和车辆评估时各轴几何关系
当车轴组数量足够多时,同时作用于某跨距桥梁上的载荷有多种组合工况:工况1为右支点位于1号轴右侧;工况2为右支点位于1号轴与2号轴之间;工况3为右支点位于2号轴与3号轴之间;工况4为右支点位于3号轴与4号轴之间;工况5为右支点位于4号轴与5号轴之间;工况6为右支点位于5号轴与6号轴之间;工况7为右支点位于6号轴与7号轴之间;其余各工况右支点位置按上述规律依次类推。
由图2可知,300LA活载评估时,当右支点位于6号轴与7号轴之间时,载荷组合工况与工况3相同,当右支点位于7号轴与8号轴之间时,载荷组合工况与工况4相同。自工况3开始,载荷组合以4个工况间隔循环重复出现。因此,300LA活载评估时的载荷组合工况共6种,车辆载荷评估时,因机车轴载荷不参与评估计算(F1=F2),此时d2为车辆固定轴距。显然,当右支点位于5号轴与6号轴之间时,载荷组合工况与工况2相同,当右支点位于6号轴与7号轴之间时,载荷组合工况与工况3相同,自工况2开始,载荷组合以4个工况间隔循环重复出现。因此,车辆载荷评估的载荷工况共5种。
2.2 剪力和弯矩计算
图3为载荷效应计算受力示意图。由图2和图3可知,当N=1时,d1=0;当N≥2时,n号轴与1号轴的轴间距dn可按式(1)计算:
dn=d2+int[(n-2)/4]·b4+b(z)
(1)
其中,z=mod[(n-2),4],当z=0、1、2、3时,b(z)分别等于0、b1、b2、b3。
本文所述桥梁为简支梁,虽各工况的载荷组合存在差异,但其两端支反力及各载荷对应截面弯矩的计算方法相同。图3为300LA活载作用下和评估车辆载荷作用下的桥梁受力情况。为统一计算公式,当该图用于计算300LA载荷效应时,F1和F2分别为机车轴重和车辆轴重;用于新设计车辆评估时,F1和F2均为车辆轴重,F1=F2。
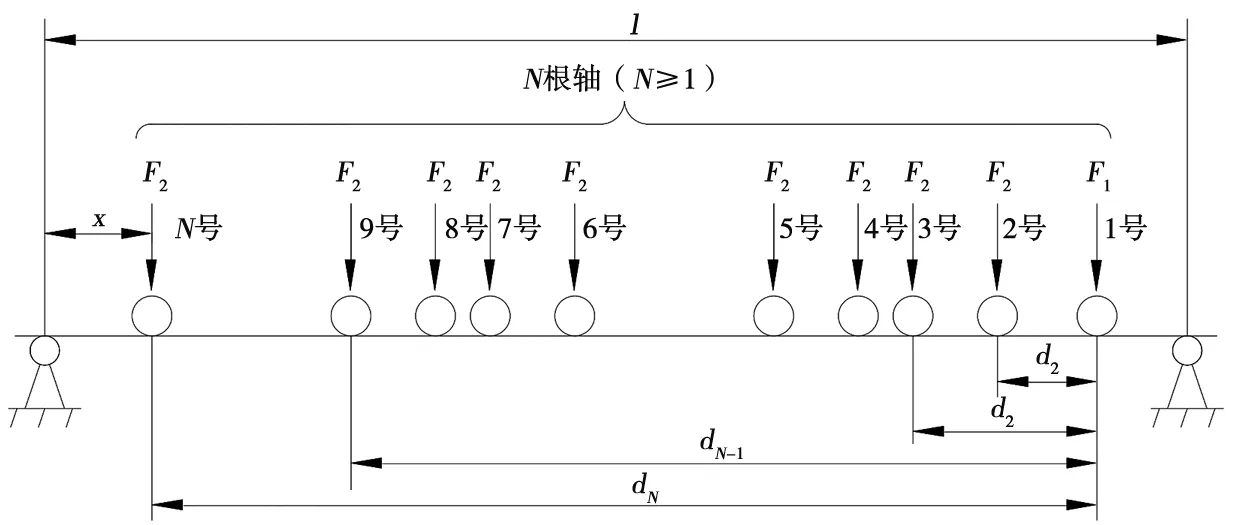
N.同时作用于桥梁上的轴数量;x.左侧第1个载荷距左支点的距离。图3 载荷效应计算受力示意图
由材料力学理论可知,桥梁左右两端的支反力将随l、j、N和x变化而变化(j代表工况编号),是以l、j、N和x为变量的多元函数;各载荷对应截面的弯矩将随l、j、N、x和n变化而变化,是以l、j、N、n和x为变量的多元函数。将左端支反力函数记为FL(l,j,N,x),右端支反力函数记为FR(l,j,N,x),弯矩函数记为M(l,j,N,n,x)。各自变量取值范围为:l为正整数,1≤l≤136;j为正整数,1≤j≤6;N、n为正整数,且N≥1,n≥1,n=j+N-1;0≤x≤l-dN。
2.2.1 剪力
根据受单个集中载荷或多个集中载荷作用的简支梁剪力图可知,最大剪力位于具有较大支反力的支点与其相邻集中载荷作用点间,与该支点支反力大小相等,方向相反。因此,欲求剪力,需先计算桥梁两端支反力。
由于F1仅在工况1(j=1)存在,为识别F1是否存在,且便于统一计算公式,引入函数q(j)、g(j,N),同时规定:当j=1时,q(j)=1,否则,q(j)=0;当j=1、N=1时,g(j,N)=0,否则,g(j,N)=1。在N个载荷作用下,跨距为l的桥梁各工况下的左右两端支反力按式(2)计算。由式(2)可知,不同的l、j、N将有不同的支反力函数与之对应,当l、j、N为定值时,函数FL(l,j,N,x)、FR(l,j,N,x)为一元一次函数,将两函数的一次项系数分别记为k和-k,常数项分别记为BL、BR,则式(2)可简化为式(3),式(3)中的k、BL、BR值分别按式(4)计算。
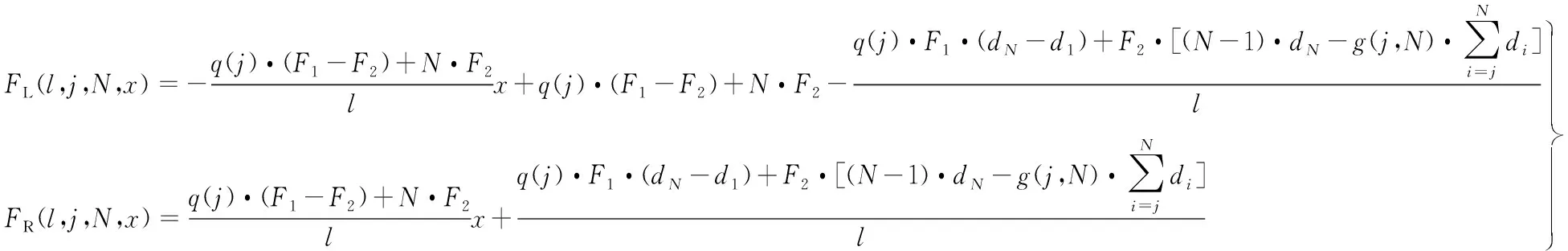
(2)
(3)
(4)
FL(x)的斜率小于0,其最大值为x取最小值时的函数值;FR(x)的斜率大于0,其最大值为x取最大值时的函数值。因此,令d1=0,跨距为l的桥梁两端最大支反力按式(5)~式(10)计算。
(1) 当j=1,dN+1-d1≥l,0≤x≤l-dN时:
(5)
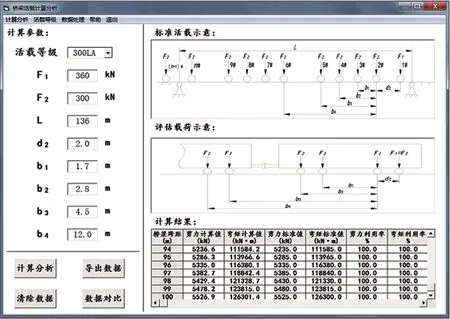
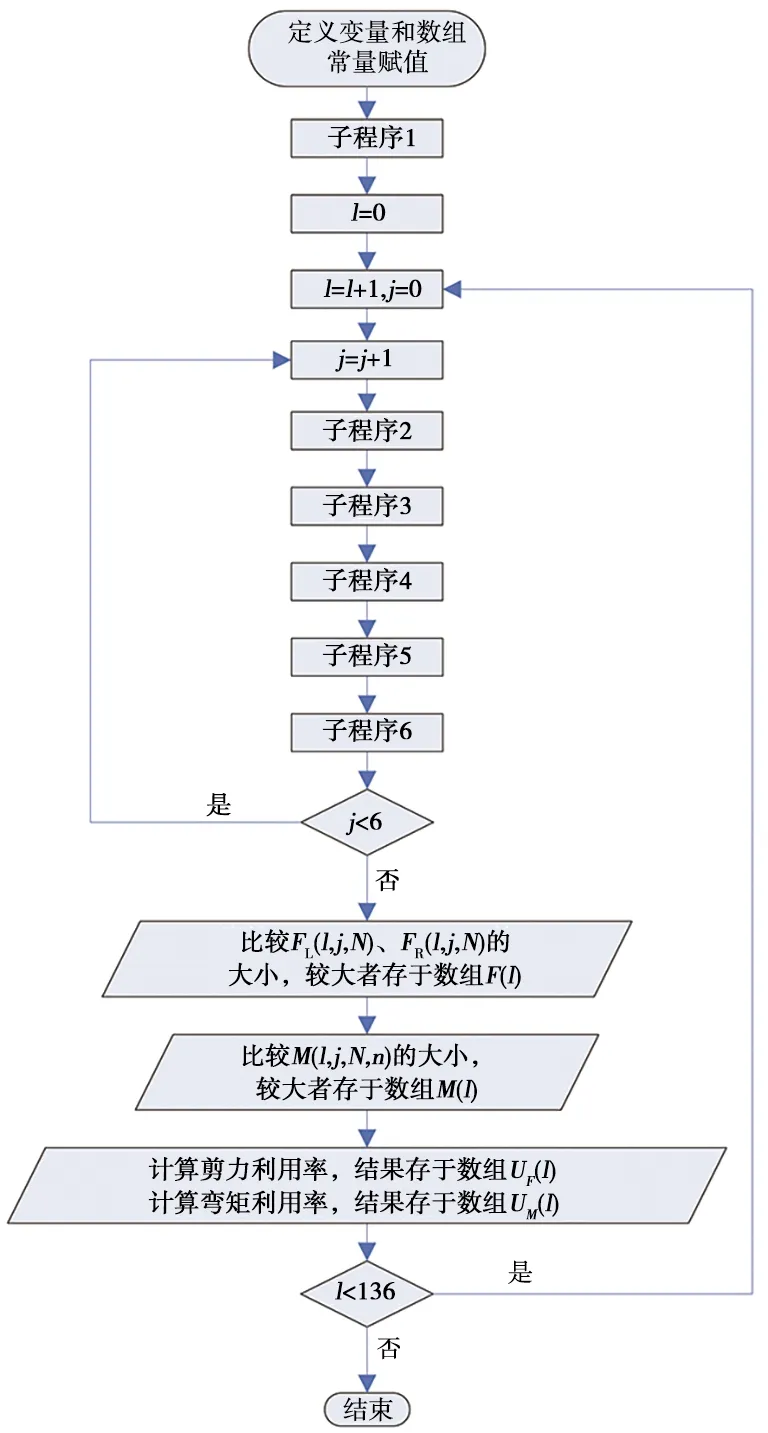
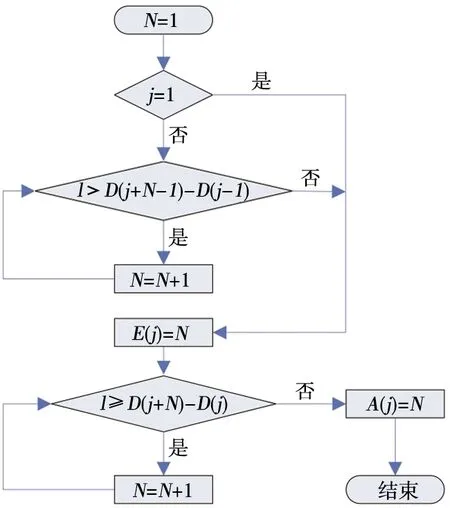
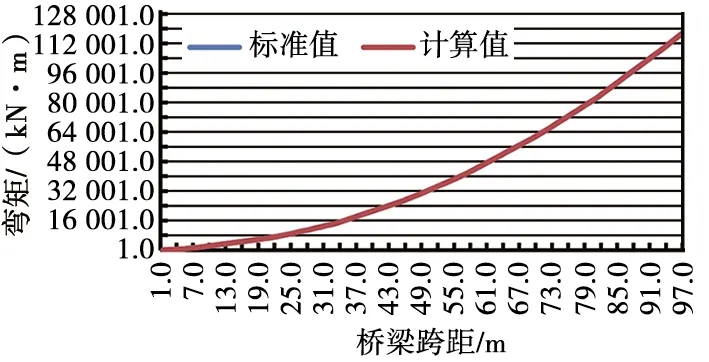
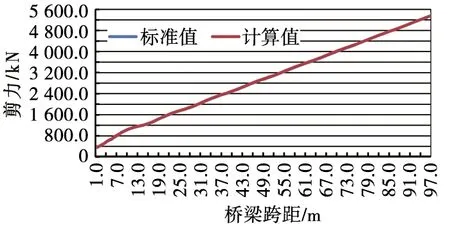
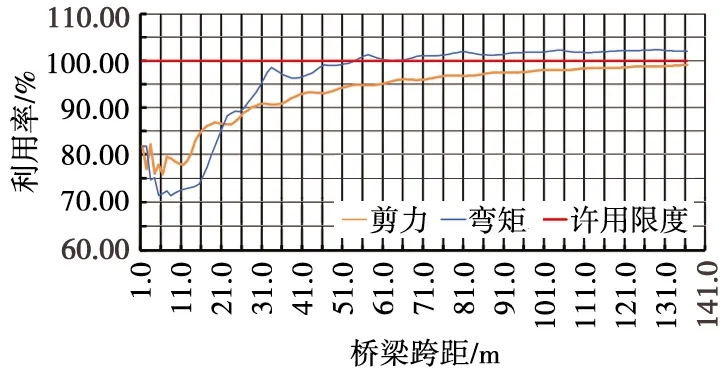
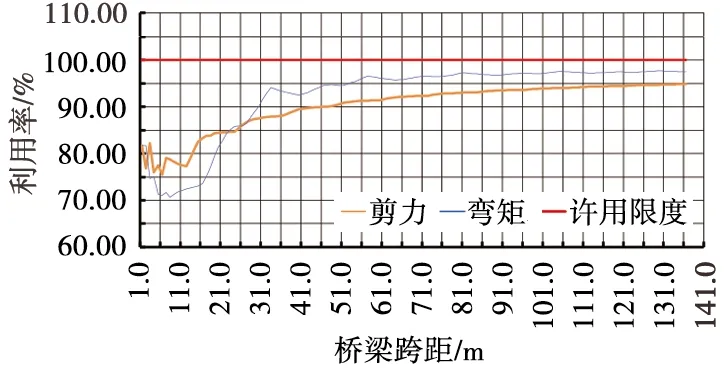
(2) 当j=1,dN+1-d1 (6) (3) 当j>1,dj+N-dj≥l、dj+N-1-dj-1≥l,0≤x≤l-(dj+N-1-dj) 时: (7) (4) 当j>1,dj+N-dj≥l、dj+N-1-dj-1 (8) (5) 当j>1,dj+N-dj (6) 当j>1,dj+N-dj (10) 2.2.2 弯矩 跨距为l的桥梁,在N个载荷作用下,将工况j第n轴载荷对应截面弯矩记为M(l,j,N,n,x),其中n=j+N-1,各载荷对应截面的弯矩按式(11)计算。 (11) 由式(11)可知,当l、j、N为定值时,第n号载荷对应截面的弯矩是以x为自变量的一元二次函数,将一次项系数记为B(n),常数项记为C(n),则式(11)可简化为式(12),式(12)中的B(n)、C(n)值分别按式(13)和 式(14)计算。 M(n,x)=kx2+B(n)x+C(n) (12) (13) (14) 函数M(n,x)的二次项系数k小于0,其图像开口向下。将自变量x的取值区间记为[XL,XR],M(n,x)max按式(15)~式(17)求解。 (15) (16) (17) 通过式(5)~式(10)和式(15)~式(17)求出跨距为l的桥梁在各工况下左右两端的最大支反力和各载荷对应截面弯矩的最大值并进行比较,最大支反力中较大者为跨距l的最大剪力,最大弯矩中较大者为跨距l的最大弯矩,分别记为F(l)、M(l)。将标准活载下跨距l的最大剪力记为Fmax(l),最大弯矩记为Mmax(l),剪力利用率UF(l)和弯矩利用率UM(l)按式(18)计算。 (18) 根据校核准则,当UF(l)、UM(l)均不大于100%时,新设计车辆载荷效应符合标准的规定;当UF(l)、UM(l)中任一值大于100%时,新设计车辆载荷效应不符合标准的规定,需对车辆长度、车辆定距、固定轴距或轴重等参数进行调整。 基于上述计算模型,标准活载和车辆评估的载荷效应计算可统一为相同的计算程序。当程序用于300LA活载或其他等级活载载荷效应计算时,F1的输入值为模拟机车轴轴重,F2的输入值为车轴组轴重;当用于车辆评估时,F1和F2的输入值均为所评估车辆的轴重,计算程序人机交互界面如图4所示。 图4 计算程序人机交互界面 计算程序由1个主程序和6个子程序组成,主程序流程如图5所示。 图5 主程序流程 (1) 子程序1:按式(1)计算出d2、d3,…,dn的值,并将d1=0和d2、d3,…,dn的值依次储存于数组D(n)。 (2) 子程序2:计算跨距为l的桥梁在工况j下车轴数量为N的最小值和最大值,并分别储存于数组E(j)、A(j),其计算流程如图6所示。 图6 子程序2流程 (3) 子程序3:按式(4)计算跨距为l的桥梁在工况j下,当E(j)≤N≤A(j)时,左右两端支反力函数的一次项系数和常数项,并分别储存于数组K(l,j,N)、BL(l,j,N)、BR(l,j,N)。 (4) 子程序4:按式(5)~式(10)计算跨距为l的桥梁在工况j下,当E(j)≤N≤A(j)时,x取值区间的左端点值和右端点值以及左右两端支点的最大支反力值,并分别储存于数组XL(l,j,N)、XR(l,j,N)、FL(l,j,N)、FR(l,j,N)。 (5) 子程序5:按式(13)和式(14)计算跨距为l的桥梁在工况j下,当E(j)≤N≤A(j)时,各载荷对应截面弯矩函数的一次项系数和常数项,并分别储存于数组B(l,j,N,n)和C(l,j,N,n)。 (6) 子程序6:按式(15)~式(17)计算跨距为l的桥梁在工况j下,当E(j)≤N≤A(j)时,各载荷对应截面的最大弯矩,储存于数组M(l,j,N,n)。 采用上述程序对基准活载300LA在跨距为1~136 m的桥梁上产生的最大静态剪力和弯矩进行验算,验算结果与AS 5100.2:2017附录C表C2中所列1~136 m桥梁的最大静态剪力和弯矩基本相同,仅在个位和十分位出现细微差异。经统计分析,本程序的各计算值与标准值的最大差异不大于0.05%,差异非常小。出现差异的原因是标准所列各值均为圆整后的数据,其个位为0或5,十分位均为0,本程序计算值精确至十分位,十分位数字不全为0。 图7和图8为根据基准活载300LA桥梁跨距的标准弯矩、剪力和采用本文所述程序计算所得的弯矩、剪力曲线图对比。可以看出,标准弯矩、剪力与计算所得弯矩、剪力的曲线基本重合,表明本文所述计算程序的计算方法正确,计算结果可信。 图7 300LA的弯矩标准值和程序计算值曲线图对比 图8 300LA的剪力标准值和程序计算值曲线图对比 2020年,中车眉山车辆有限公司与澳大利亚某公司签订了石砟漏斗车供货合同,合同技术规范要求该车采用25 t轴重转向架,桥梁活载等级为260LA。根据技术规范要求及底门和漏斗布置需要,初始设计方案的车辆长度为11.7 m,车辆定距为7.2 m,采用25 t轴重的符合AAR标准要求的固定轴距转向架,固定轴距为1.727 m。采用本程序进行评估,结果表明,该方案车辆长度、车辆定距、轴重等满足260LA活载要求(图9)。 图9 初始方案在活载260LA下弯矩及剪力利用率 但在项目图样审查时,用户提出增加在活载为230LA线路上运行的额外需求,希望其运用轴重达到23 t。用户需求变更后,根据本程序计算结果,当桥梁跨距大于53 m时,弯矩利用率超过100.00%(图10),不满足在230LA活载桥梁上运用轴重为23 t的要求,需要改变其车辆长度、车辆定距或邻轴距等参数。 图10 初始方案在活载230LA下弯矩及剪力利用率 采用本程序进行了多轮试算,发现车辆长度不变、仅改变邻轴距或车辆定距对降低大跨距桥梁载荷效应的效果不显著,而增加车辆长度和车辆定距的效果更显著。根据本程序计算结果,将车辆长度增加至12 m、车辆定距增加至7.7 m后,在230LA活载桥梁上的运用轴重可达23 t ,此时最大弯矩和剪力均不超过许用值,且弯矩和剪力均有一定裕量(图11),很快得到用户的认可。根据本程序计算结果编制的桥梁载荷效应评估报告得到了澳大利亚铁路管理当局认可,方案顺利通过设计认证,为按时兑现合同奠定了坚实基础,同时为企业赢得了足够时间以完成更改设计。 图11 新方案在230LA下弯矩及剪力利用率 本文提出了桥梁在标准活载和评估车辆载荷作用下所受最大静态剪力和弯矩的计算方法,推导了相关的计算公式,编写了校核计算程序。验证计算和计算实例表明,本文设计的计算方法正确,程序计算结果满足澳大利亚铁路桥梁垂向活载校核精度需求。在项目初期及初步方案设计阶段,设计人员可利用该程序快速选择轴重、车辆定距、邻轴距等关键技术参数,对用户需求作出及时回应;在项目执行阶段,可运用该程序计算结果准确地撰写桥梁车辆载荷效应评估报告,以确保项目设计方案通过铁路管理当局认证。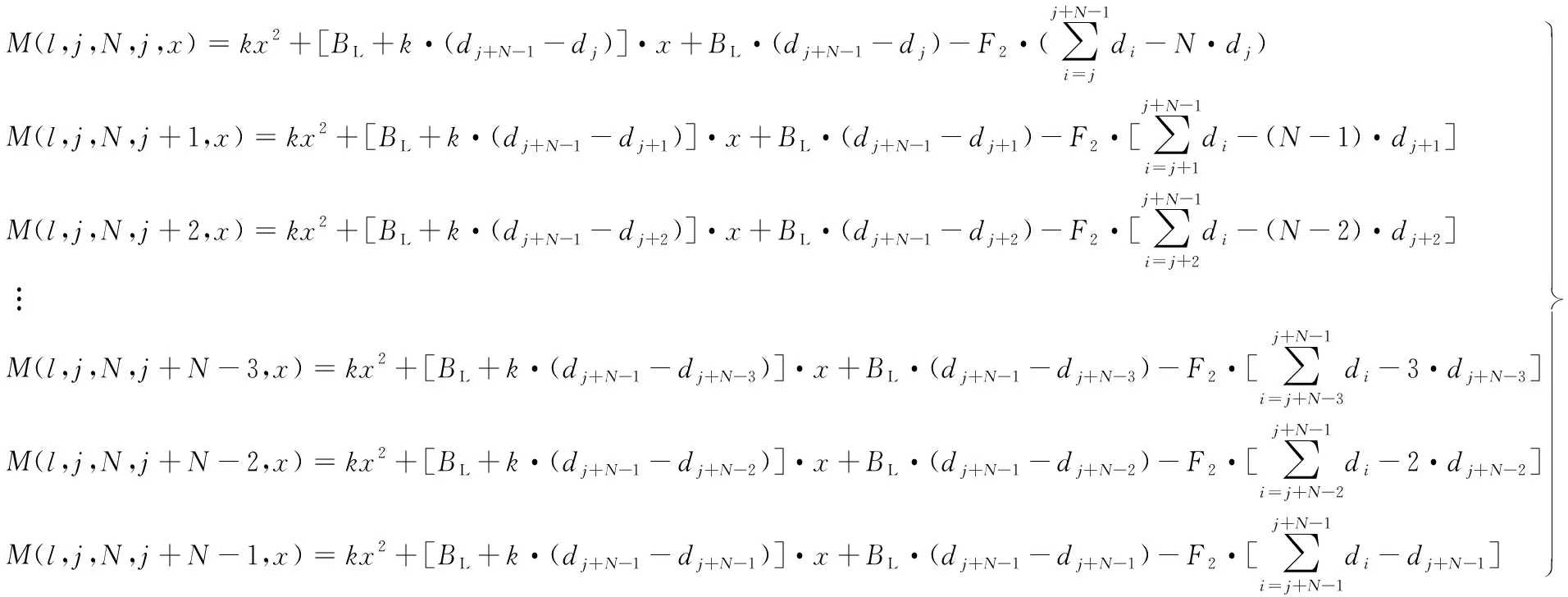
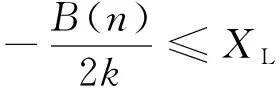
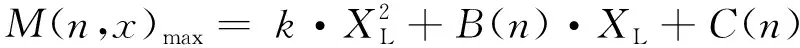
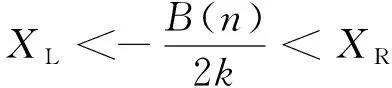
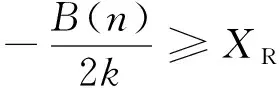
2.3 车辆评估
3 计算程序
4 计算验证及运用实例
4.1 计算验证
4.2 运用实例

5 结束语
