指向数学核心素养的任务设计
——以抛物线的性质为例
2021-11-09上海
上海 宋 磊
《普通高中数学课程标准(2017版2021年修订)》明确指出:“高中数学课程以学生发展为本,落实立德树人根本任务,培育科学精神和创新意识,提升数学学科核心素养.”数学核心素养的理念一经提出,热度一直不减.如何真正让数学核心素养在课堂落地生根是一线教师关注的焦点,也是进行教学活动的出发点.在渗透数学核心素养的目标之下,“教什么”与“怎么教”是一线教师需要思考的热点问题,也是进行教学活动的落脚点.理念没摆正、问题没弄清楚,结果还会与以往一样,那基于核心素养的理念下的教学无疑是“新瓶装旧酒”“穿新鞋走老路”.
为了使基于核心素养的课堂教学有效实施,史宁中教授认为:“应遵循两个原则.一是把握数学的本质,二是设计并且实施合理的教学活动”.而教学设计是教学活动的先行者,有利于学生感悟、理解、形成和发展核心素养,笔者认为,唯有从描述核心素养水平的四个维度“情境与问题”“知识与技能”“思维与表达”“交流与反思”着手进行教学设计和教学实践,才是正确的路径和方法.本文以“抛物线的性质”为例来探讨如何基于数学与核心素养进行有效的教学设计.
一、案例
课题:曲线的参数方程
设计目标:
1.认知目标:感受抛物线在实际生活中的广泛应用,掌握抛物线标准方程的求法,会利用抛物线的性质解决实际问题.
2.能力目标:依据问题情境,尝试数学建模过程,提高合情推理能力,体验基本“科研”方法.
3.育人目标:通过“做数学”开展探究,感悟数学的魅力和力量,初步了解如何用数学思维去思考世界,用数学语言去表达世界,用数学工具去改变世界.
任务重点:
根据问题情境和题设条件引入合适的参数,建立抛物线的方程,体会学习数学的重要意义并激励学生主动参与、相互协作、探索研究的精神.
任务难点:
从生活实际问题中抽象数学概念、建模并用数学的思维方式进行探究.
(一)情境与问题
情境:2020年4月20日00时30分,上海市普陀区真北路1531号,成功爆破四幢“烂尾楼”.这四幢主体均超过20层楼,其中两幢高达106米,另外两幢也有90多米高,爆破面积达18万平方米.这次的爆破任务要将同一地点四幢高层于同一时间爆破,难度非常大,在国内尚属首例.且由于紧邻商业中心、高架和居民区,周边环境复杂,对爆破行动有非常高的要求.据工作人员介绍,这次爆破使用了7吨炸药,排布了5天.
问题:为了确保爆破的质量和安全,如何确定爆破的安全区和危险区?
(二)知识与技能
知识:
平面上与一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,定直线l叫做抛物线的准线.
技能:
【例1】求以坐标原点为顶点,焦点在坐标轴上且经过点M(-2,-4)的抛物线的方程.
解:若抛物线的焦点在x轴上,根据条件可设抛物线的方程为y2=-2px(p>0).因为点P(-2,-4)在所求的抛物线上,所以(-4)2=-2p·(-2).解得p=4.故抛物线的方程为y2=-8x.

即所求抛物线的方程为y2=-8x或x2=-y.
【例2】求过定点M(0,1)且与抛物线y2=2x只有一个公共点的直线的方程.



显然,过点M(0,1)且垂直于x轴的直线x=0也满足题意.

(三)思维与表达
1.整理思维
通过上述两例的学习,我们掌握了如何求抛物线的标准方程,以及解决了直线与抛物线的位置关系的问题.在上述情境问题中,爆破物的运动轨迹是一系列不同的抛物线,它们构成一个抛物线系,这些抛物线不会越出一定的范围.因此,在这样的范围以外是安全区,那么这个安全边界如何来求?
2.数学建模
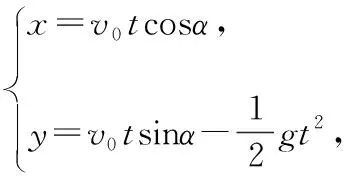

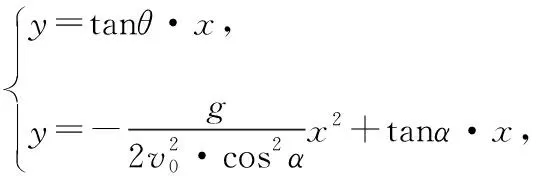
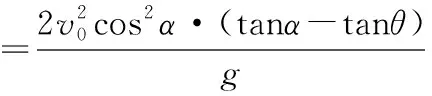
当给定θ的值后,M(x,y)随着α的变化而变化.当sin(2α-θ)=1时,交点M的纵坐标y最大,对应的横坐标x的绝对值也最大,此时交点坐标为M0(x′,y′),即
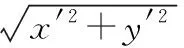

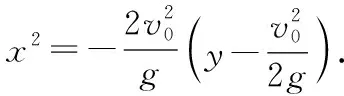
3.问题解决
(1)信息收集
在爆破工程中确定安全区和危险区是一项非常复杂的工程,必须要考虑地质、地形及炸药性能等因素,但是爆破点处炸开的矿石等爆破物的运动轨道是一系列不同的抛物线.
(2)基本假设
①不考虑地质、地形以及炸药性能等因素,假设作业人员每个操作步骤都规范、安全.
②爆破作业有效防治爆破震动产生的巨大危害.
③爆破作业有效防治爆破产生的空气冲击、有毒气体排放等危害因素.
(3)模型运用
(四)交流与反思
1.模型反思
(1)模型另解
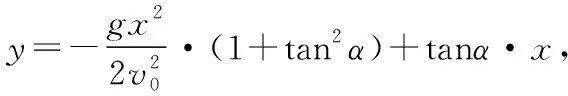
化简整理,得
上式α有唯一解,由b2-4ac=0,可得
整理得安全抛物线的方程为
(2)模型反思

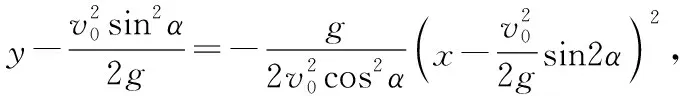
由此可得,质点的轨迹是顶点为
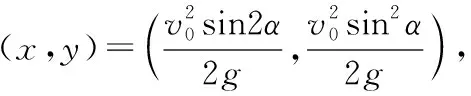
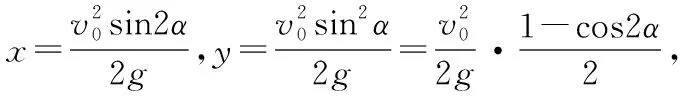
将两式平方相加消去参数α,可得
小结:本课题的设计是基于对生活实际问题的思考,是抛物线在实际生活中的应用.在体验与感悟中学习知识、掌握技能、培育能力.通过对解题思维的整理,引发深度思考.在生活实际问题的解决过程中,渗透数学抽象、逻辑推理、直观想象、数学运算和数据分析等核心素养.
二、结语

