解析几何教学中发展学生数学运算素养的思考

北京 相文明 王长友

每年高考的解析几何综合问题是牵动广大师生敏感神经的重头戏，此题既体现出命题者的立意对教学的导向引领，同时引导学生欣赏圆锥曲线优美的性质进而感悟解析法的无穷魅力，而解决此问题的基础是学生的数学运算素养，因此在日常教学中教师必须系统思考、科学设计与规划，进而实现发展学生的数学运算素养.

一、典型问题再现

(Ⅰ)求椭圆E的标准方程；

(Ⅱ)过点P(0,-3)的直线l的斜率为k，交椭圆E于不同的两点B,C，直线AB交y=-3于点M,直线AC交y=-3于点N，若|PM|+|PN|≤15时,求k的取值范围.

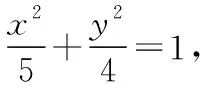
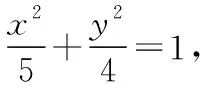
(2)方法一：设直线l:y=kx-3，B(x1,y1),C(x2,y2),M(xM,-3),N(xN,-3),

(4+5k2)x2-30kx+25=0，400k2-400>0,

即k<-1或k>1,

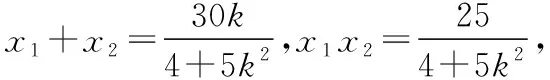
且Δ=(30k)2-4×25(4+5k2)=400(k2-1)>0，

得|k|>1，

又由A,B,M三点共线得kAM=kAB，

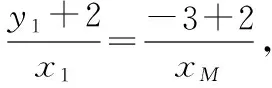
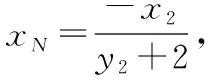
因为|PM|+|PN|=|xM|+|xN|，

且显然y1+2>0,y2+2>0，

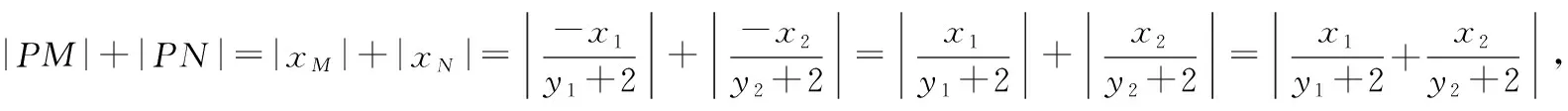
又因为y1=kx1-3,y2=kx2-3分别代入，化简得

化简得|k|≤3,

所以k的取值范围是[-3,-1)∪(1,3].

方法二：将原问题条件转化为“过A作两条直线AB,AC与椭圆交于B,C且满足P,B,C三点共线”即可.

设直线AB的方程为y=mx-2，直线AC的方程为y=nx-2，易知m,n存在且m≠0,n≠0,m≠n.

设B(x1,y1),C(x1,y1),M(xM,-3),N(xN,-3),

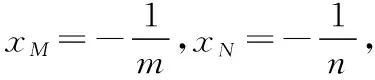
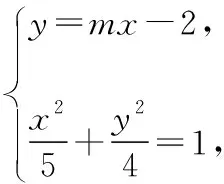
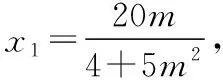
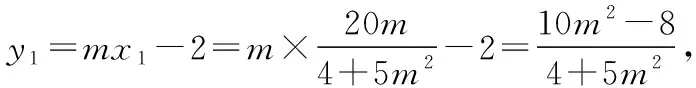
又因为P,B,C三点共线，即kBP=kCP,

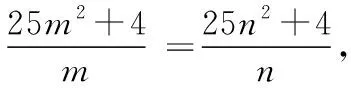
进一步化简，并整理得25mn(m-n)-4(m-n)=0，

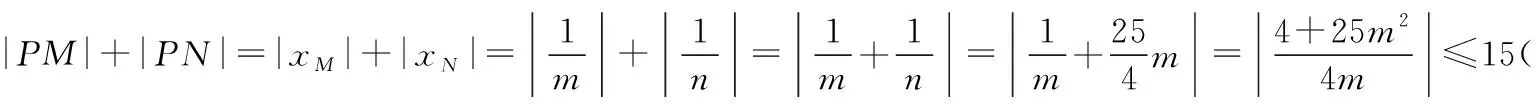
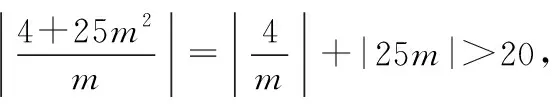
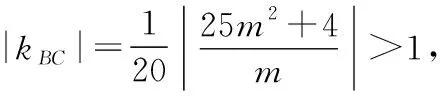
综上，1<|kBC|≤3,所以k的取值范围是[-3,-1)∪(1,3].

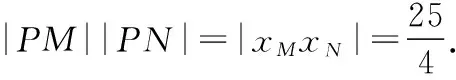
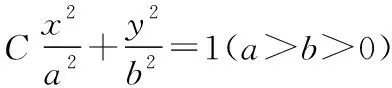
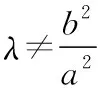
证明：设直线l:y=kx+m，A(x1,y1),B(x2,y2),P(x0,y0)，

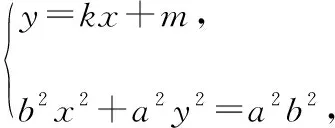
(b2+a2k2)x2+2kma2x+a2(m2-b2)=0，

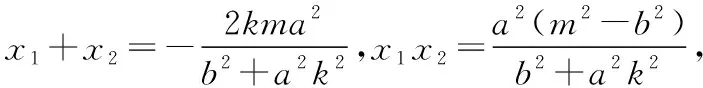
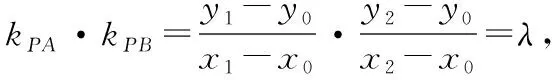
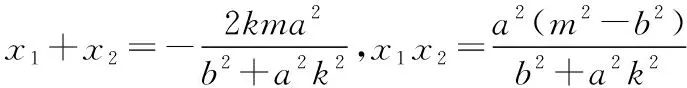
进一步整理(按照R的降幂排列)，得

变形整理，有[(kx0-(y0-m)][(λa2+b2)x0k+(λa2+b2)y0+(λa2-b2)m]=0,

显然kx0+m-y0≠0(因为P∉l)，所以(λa2+b2)x0k+(λa2+b2)y0+(λa2-b2)m=0,

再整理(b2-λa2)m=(λa2+b2)(kx0+y0).

①若x0=0，显然y0≠0，说明直线l的斜率不存在，即直线l垂直于x轴;

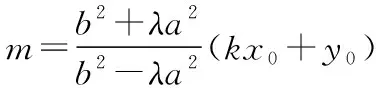
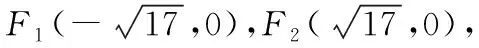
(1)求C的方程；

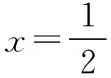
(1)因为|MF1|-|MF2|=2，所以轨迹C为双曲线右半支，c2=17，2a=2，

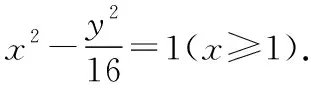
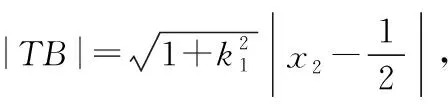
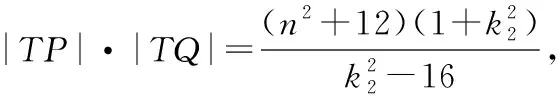
|TA|·|TB|=|TP|·|TQ|，

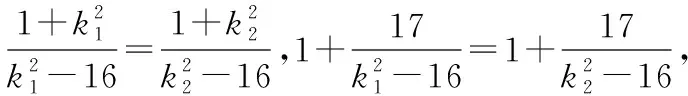
因为k1≠k2，所以k1+k2=0.

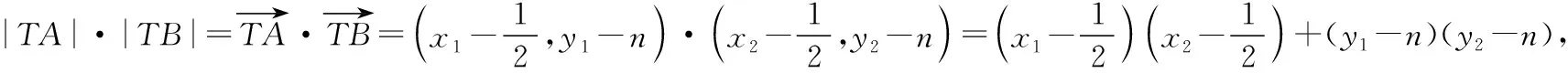
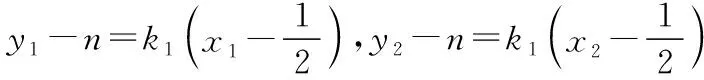
其他过程同方法一.

结合两道高考试题及引申思考问题的特点，容易发现研究距离问题是解析几何重要的考查内容，而解析几何综合问题中常见距离问题的刻画均需要有较强的运算素养.在上述问题的解决中学生反馈的难点有三个：

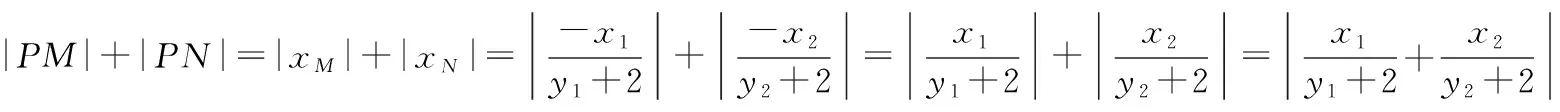
需要按照k的降幂排列整理方程等.

结合命题考查特点与学生问题、难点说明，教师在教学中必须有效落实数学运算素养的培养.

二、教学思考

高考命题要体现“一核四层四翼”， “一核”是高考的核心功能，即“立德树人、服务选才、引导教学”；“四层”为高考的考查内容，即“核心价值、学科素养、关键能力、必备知识”；“四翼”为高考的考查要求，即“基础性、综合性、应用性、创新性”.解析几何的综合问题是优良的考查载体，而数学运算素养恰恰是基础与关键，这就要求教师要不断主动思考，一方面教师对数学运算素养的理解站位要高，另一方面教师要落脚更实，合理规划数学运算素养的培养路径，引导学生在学习过程中内化.

(一)解析几何中数学运算素养的理解

1.课标要求

数学运算是指“在明晰运算对象的基础上，依据运算法则解决数学问题的素养.主要包括：理解运算对象，掌握运算法则，研究运算思路，选择运算方法，设计运算程序，求得运算结果”.

结合解析几何的研究特征即“借助几何图形特点，形成解决问题思路，通过直观想象和代数运算得到结果”，数学运算既是研究的方法又是检验学生运算素养水平效果的基石.

2.解析几何中运算素养的基本层次理解

解析几何教学中要重点关注“理解运算对象、研究运算思路、选择运算方法”三个角度，学生数学运算素养的落实要体现差异性、层次性，是教师主动指导与设计培养的螺旋式上升的实施过程.教学中，教师一方面理解学生即学生的个体差异是客观事实，另一方面要把数学运算分解为有针对性、具体性、操作性的目标.

3.整体把握教材内容设计中要求的数学运算素养

教学内容是直线与方程、圆与方程、圆锥曲线与方程三个层面设计，基本逻辑是由易到难、由直观到抽象、由经验到理性的学习过程.其中体现的运算要求为直线与圆的章节侧重能用代数方法运算处理问题并体会运算的合理选择、准确操作等；圆锥曲线侧重理性思考运算的对象、运算的策略与思路、运算的方法与求解，要求学生养成准确、合理、简洁、迅速的运算习惯，并能体会数学运算在解决数学问题中的价值.

(二)解析几何中落实数学运算素养的策略与方法思考

解析几何的问题几乎处处离不开运算，学生的运算素养直接制约着教学目标是否实现，教师在教学中要明确基本的运算素养培养策略.

1.以数学逻辑推理为根本指导运算素养

章建跃先生认为：数学学习的基本任务是学会运算和推理，运算离不开推理，推理在高中乃至整个基础教育阶段的数学学习中的展现形式就是运算.会推理才能运算是基本共识，而具体在解析几何教学中，就是要让学生明白“研究对象是谁？研究对象间的关系如何刻画？为什么要合理选择代数关系刻画图形特征？运算的目标与方向是什么？达成的路径是否准确与合理？”等基本问题.

教师要充分意识到逻辑推理是产生运算的思维基础，学生只有条理清晰才能在运算的算法操作中明方向、懂算理.解析几何综合问题的逻辑基础是参数选择的准确性(能否用参数串联表述问题)、合理性(算法是否简洁)，重点是条件与结论的合理翻译转化，标准就是数学运算的可行性、操作程序的简便性.

2.以算法为依托主动分析运算的效能

解析几何研究的运算对象较多，教学需要引导学生从关系入手，寻找连接点，合理设计或构造运算程序与选择运算方法，即“算什么？怎么算”.

(1)建立算法整体观

解析几何的问题更多是选择合理参数，以“设而不求、寻找联系”为出发点与落脚点，养成整体算法思考是学生必须掌握的技能.基本算法的共性是明确运算对象的方向、厘清运算的途径与关系即整体考虑算法，重点关注运算过程中的方程本质，明确代数变形中的“主元与结构特征”.

(2)明确运算方向优化算法

运算方向决定运算程序，解析几何问题要引导学生首先分析、思考运算的方向，进而确定运算目标与运算方法，本质是数学简洁美的体现.

(3)掌握运算策略简化算法

解析几何运算策略的重要体现：一为定性与定量的结合，关注定性明方向，关注定量求准确；二是要时刻进行化繁为简；三是整体代换重视运算结构.

3.以几何性质为线索实现运算的优化

解析几何的本质是用代数方法研究几何问题，自然而然解决问题中要关注几何图形的性质与特征，熟练学会合理挖掘几何性质简化运算量.

4.以常规运算为载体逐步提升运算素养

解析几何与运算形影不离，教师要分阶段、分层次的设计实施.从数字的计算到字母的运算、从代数式的化简到距离、角、位置关系等基本量的代数刻画与求解、从简单模仿到主动思辨、从关注运算结果到探究运算思路(包括分析运算条件、探究运算方向、选择运算方法、设计运算程序)等.

5.以学生的意志品质为生长点实现运算素养的落实

学生运算素养的提升是最终的目的，学生的主动性与个性品质是关键，教师教学中要关注学生的认识、理解与感悟.一方面，教师要设计不同情境问题与学习方式激发学生需求与内驱力，让学生想做；另一方面，教师要差异化设计与积极评价学生的进步与增长点，让学生有成就；第三方面，教师要高位引领，给学生具体有效的指导，让学生有收获.