2021年全国乙卷理科第21题解法探究与背景溯源

安徽 刘守文

一、试题呈现

(2021·全国乙卷理·21)已知抛物线C:x2=2py(p>0)的焦点为F，且F与圆M:x2+(y+4)2=1上点的距离的最小值为4．

(1)求p；

(2)若点P在M上，PA,PB是C的两条切线，A,B是切点，求△PAB面积的最大值．

二、试题第(2)问解法探究

本题的第(2)问求△PAB面积的最大值，是高考圆锥曲线常考的面积问题.考查学生对圆锥曲线基本解题方法、技能的掌握和解题基本思想的领悟，侧重学生分析和解决问题的能力.本文主要针对第(2)问进行分析.

解法1：“设而不求”法

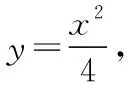
设点A(x1,y1)，B(x2,y2)，P(x0,y0)，

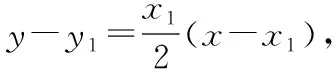
即x1x-2y1-2y=0，

同理可知，直线PB的方程为x2x-2y2-2y=0，

由于点P为这两条直线公共点，

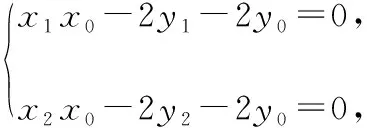
即点A,B两点的坐标均满足方程x0x-2y-2y0=0，

所以直线AB的方程为x0x-2y-2y0=0，

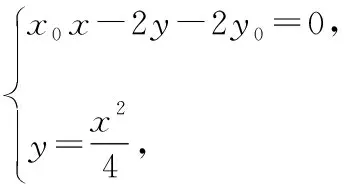
可得x2-2x0x+4y0=0，

由韦达定理可得x1+x2=2x0，x1x2=4y0，

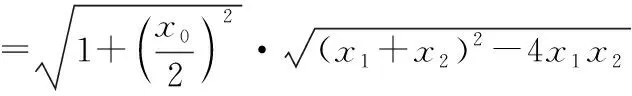
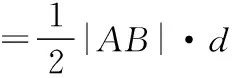
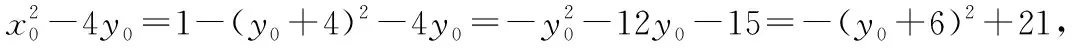
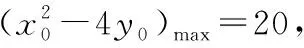
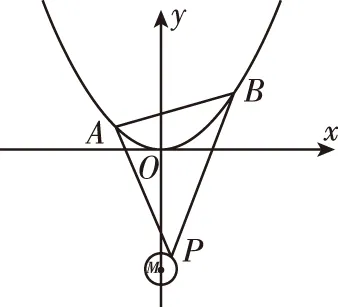
解法2：三角代换法(利用圆的参数方程)

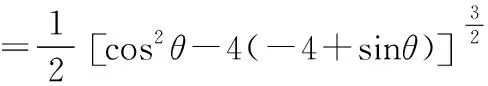
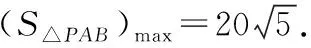
解法3：图形割补

如图,设点A(x1,y1),B(x2,y2),P(x0,y0)，

过点P作PQ∥y轴,交AB于点Q，则

由解法1可知，直线AB:x0x-2y-2y0=0，与直线PQ：x=x0联立，

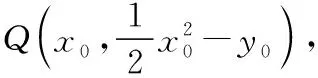
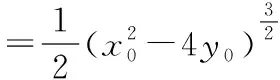
下同解法1.

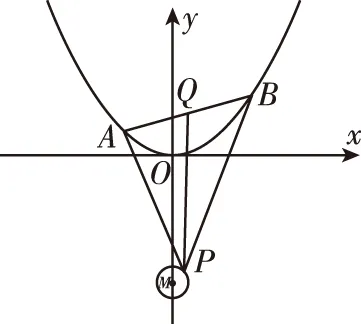
点评：解法1～3是典型的“设而不求”思想方法的运用，不同的是解法3将△PAB一分为二，方法处理上更加技巧.这几种方法是高考复习中解决圆锥曲线面积问题的通性通法，考查了学生对基础知识的掌握、基本技能的应用以及对基本思想的理解与领悟，教师教学中要注重通性通法的讲解，加强对学生“四基”的针对性训练.

解法4：三角形面积向量公式法

设点A(x1,y1)，B(x2,y2)，P(x0,y0)，

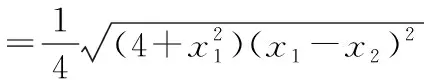
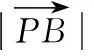
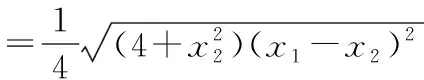
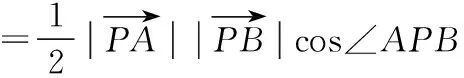
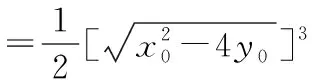
下同解法1.

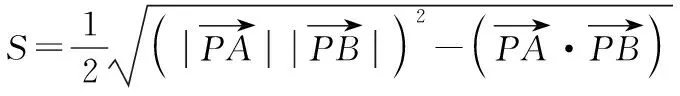
解法5：向量转化法

设点A(x1,y1)，B(x2,y2)，P(x0,y0)，

由解法1可知，直线AB：x0x-2y-2y0=0，

则直线AB与y轴交点为C,则C(0,-y0).

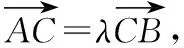
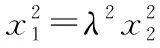
λy2+y1+(λ+1)y0=0 ②，

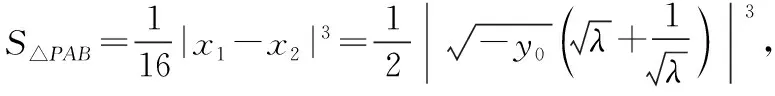
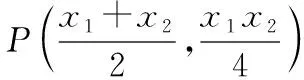
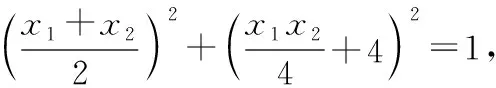
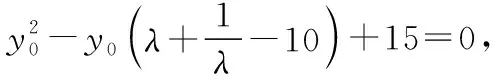
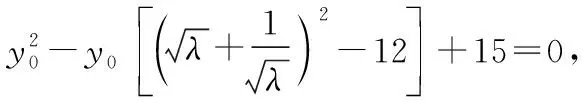
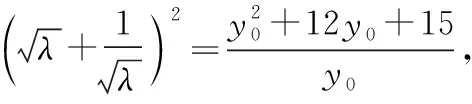
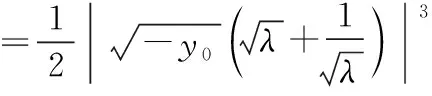
下同解法1.

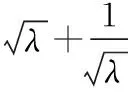
三、试题结论推广

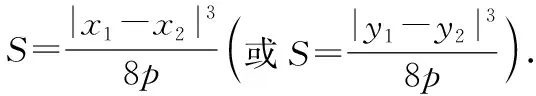
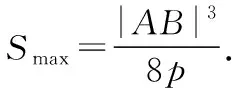
限于篇幅，此处只证明当x2=2py(p>0)时的结论，其他形式的证明过程类似.

证明：当x2=2py(p>0)时，如图所示，过点P作PQ∥y轴,交AB于点Q，

设点A(x1,y1)，B(x2,y2)，联立PA,PB的方程

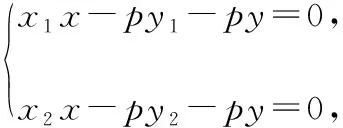
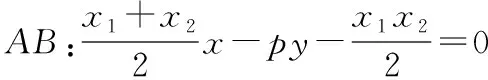
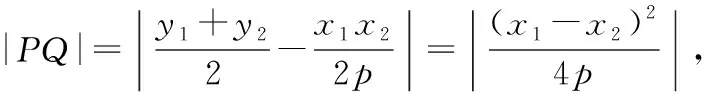
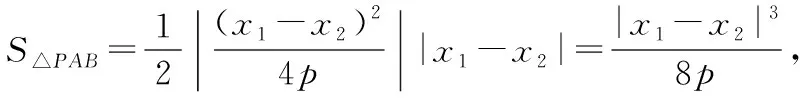
当|AB|为定值时，令点P到直线AB的距离为d，

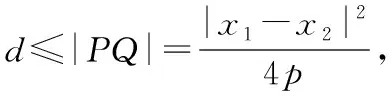
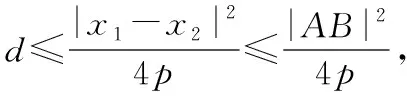
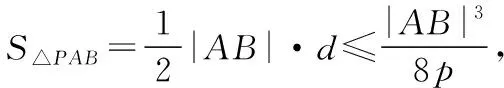
四、试题数学文化背景溯源

《普通高中数学课程标准(2017年版2020年修订)》指出: 数学文化是指数学的思想、精神、语言、方法、观点,以及它们的形成和发展.数学的形成和发展史是数学文化的重要内容，2021年高考数学全国乙卷涉及抛物线的弦与过弦的端点的两条切线所围的三角形，这个三角形又常被称为阿基米德三角形.阿基米德是古希腊伟大的数学家、物理学家，他最早用逼近的思想推出了抛物线弓形的面积,是微积分思想的先驱，享有“数学之神”的称号.阿基米德三角形内涵丰富，在数学史上具有重要地位，其重要性质一直是高考圆锥曲线命题的热点素材和高频考点，是从高考命题角度对课标理念“数学文化融入数学课程”的重要体现，其出题多以隐性形式给出.笔者归纳了近些年高考全国卷试题中阿基米德三角形的常考知识点，如下表所示.

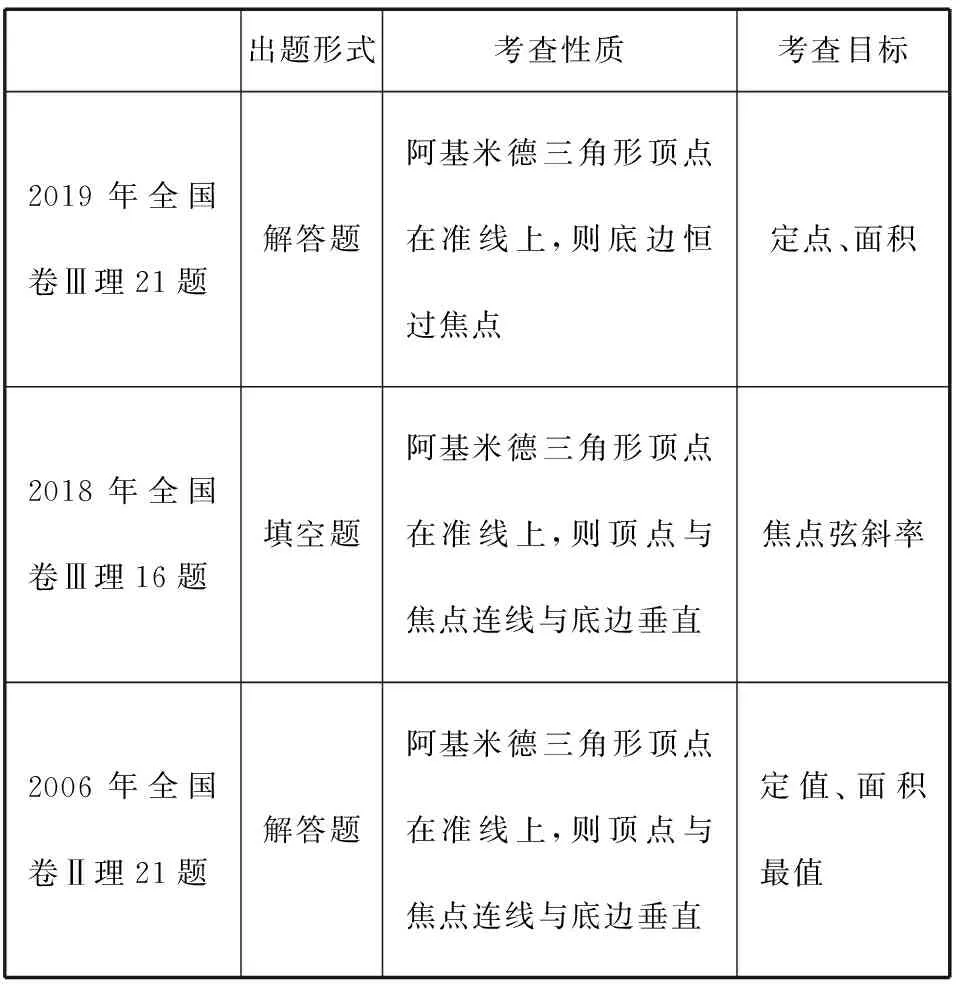
出题形式考查性质考查目标2019年全国卷Ⅲ理21题解答题阿基米德三角形顶点在准线上,则底边恒过焦点定点、面积2018年全国卷Ⅲ理16题填空题阿基米德三角形顶点在准线上,则顶点与焦点连线与底边垂直焦点弦斜率2006年全国卷Ⅱ理21题解答题阿基米德三角形顶点在准线上,则顶点与焦点连线与底边垂直定值、面积最值

阿基米德三角形在高考各省自主命题中也屡有出现，在此不再一一列举.通过归纳可以发现，试题主要运用阿基米德三角形性质考查弦长、定点(值)、轨迹、切线、面积、范围等圆锥曲线基本知识.

五、教学启发

笛卡儿的坐标系为数学发展插上了一对翅膀，坐标系将数与形完美地结合起来，诠释了数学的统一美.解析几何利用“数”的方法解决“形”的问题，通过代数运算确认几何图形的内在关系.圆锥曲线高考试题考查了数学运算能力，是发展数学运算核心素养的重要载体，是获取“四基”，提高“四能”的重要途径.对于圆锥曲线教学，有以下两点教学启发.

(一)注重通性通法研究

高考圆锥曲线试题具有运算量大，思维严谨性高的特点.教学中教师要重视通性通法的讲解，重视打牢基础知识，传授基本解题思路及技巧，渗透基本解题思想方法，提升学生分析和解决问题的能力.如2021年全国乙卷第21题，其主要考查学生对圆锥曲线解题中最一般也是最核心的思想方法——“设而不求”思想方法的理解与掌握.教师在教学中要总结常见几何图形关系的代数表征，将平面几何图形关系“翻译”成代数表达式.对于复杂问题，可以尝试分解为几个步骤，采用分步策略帮助学生理解问题.引导学生归纳、总结一般思路、一般规律.通过数学运算理清思路、拓展思维，发展数学核心素养.

(二)注重高考试题背景研究