全浸式火炮内弹道参数优化设计
2021-11-08郭映华李瑞静董彦诚
郭映华, 李瑞静, 刘 伟, 董彦诚
全浸式火炮内弹道参数优化设计
郭映华, 李瑞静, 刘 伟, 董彦诚
(西北机电工程研究所, 陕西 咸阳, 712000)
随着水下安全威胁的日益提升, 水下火炮内弹道优化设计已成为水下攻防领域的研究热点之一。火炮尤其是采用变燃速发射药的小口径火炮的水下发射过程与大气中火炮发射过程相比更加复杂。文中针对全浸式火炮发射过程, 在经典内弹道模型的基础上, 考虑钝感发射药、弹丸对身管内弹丸水柱的做功、炮口喷出水阻以及水深的影响等诸多因素建立内弹道方程组, 并选择多岛遗传算法对火炮内弹道参数进行优化设计, 得出了满足炮口初速和最大膛压要求的装填参量和发射药参数, 包括药室容积、弹丸行程长、发射药弧厚、钝感深度、表面燃速修正量和装药量等。对优化结果的工程化分析可知, 文中的设计方法可以快速得到较为合理的参数指标, 从而大幅度减小内弹道设计的工作量。
全浸式火炮; 内弹道; 水下发射; 优化设计; 多岛遗传算法
0 引言
现代海战中来自水下的安全威胁日益提升。因之各国海军的研究目标向水下发射火炮技术拓展, 以期建立不同于陆上火炮的内弹道与装药设计方法, 提高水下火炮的设计水平。在空气中研究内弹道时, 由于空气的密度很小, 身管内空气的质量与子弹的质量相比可忽略不计。而在水中, 由于水的密度约为空气的800倍, 管内水的质量往往大于弹丸本身的质量, 同时水柱喷出炮口时受到非常大的阻力(很多船只以该阻力产生的反冲力作为动力进行推进), 此外水深也对弹丸运动有一定的影响, 这些因素使得水中内弹道方程及内弹道过程规律与大气内弹道方程相比有很大变化, 针对此展开的研究成果已被应用于水下发射内弹道研究中[1-3]。例如, 孔德仁等[1]以弹丸及水柱为受压体, 建立了水下弹道的简化模型; 兰晓龙等[4]建立了考虑弹丸前端水柱流态分别为层流和紊流状态的内弹道方程组。当今, 通常采用钝感发射药提升枪炮等身管武器的主要战术指标, 钝感药替代非钝感药已成为小口径火炮研究的热点之一, 钝感发射药可以实现“压力平台”效应, 在不提高最大膛压的情况下提高弹丸初速[5-6], 所以采用钝感发射药发射水下弹丸有利于再提高弹道示压效率, 即最大膛压不变时提高炮口初速。
由于水下全浸没式发射过程的影响因素多、变化趋势更为复杂, 有些变化规律甚至与陆炮相反, 再加上采用变燃速的钝感发射药, 加大了设计难度, 所以有必要采用先进的优化算法进行方案优化设计。针对此, 文中建立了钝感发射药的水下全浸式火炮内弹道方程组, 采用多岛遗传算法进行内弹道优化设计计算, 并以30 mm火炮为例, 给出了设计目标、优化参量、优化设置及有关计算结果。
1 基本方程
1.1 模型建立
水下发射原理图如图1所示。以经典陆用火炮发射内弹道为基础[7], 根据水下火炮的特点, 建立内弹道方程组, 其中假设条件为: 1) 假设发射药床同时点火, 发射药燃烧遵循几何燃烧定律; 2) 火药燃烧及变质量体的运动与常规弹道一样, 均在平均压力下进行, 且燃烧生成物的成份保持不变, 发射药燃气状态方程服从诺贝尔-阿贝尔方程; 3) 用次要功系数考虑各种形式的次要功, 譬如炮膛摩擦力、热散失等。
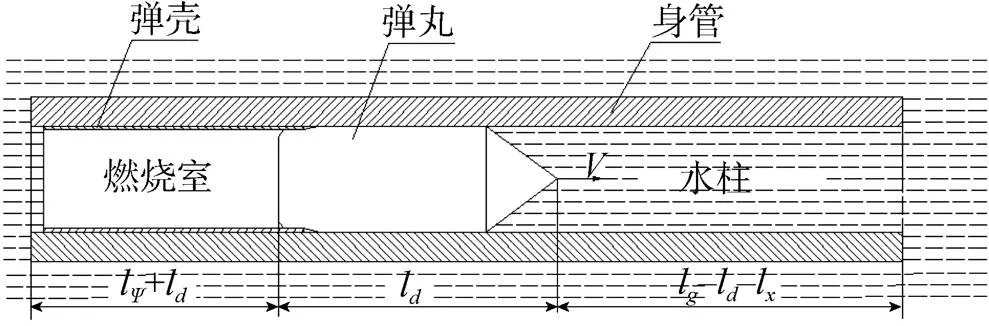
图1 水下发射示意图
1.2 数学模型
根据以上假设, 可得水下内弹道方程组
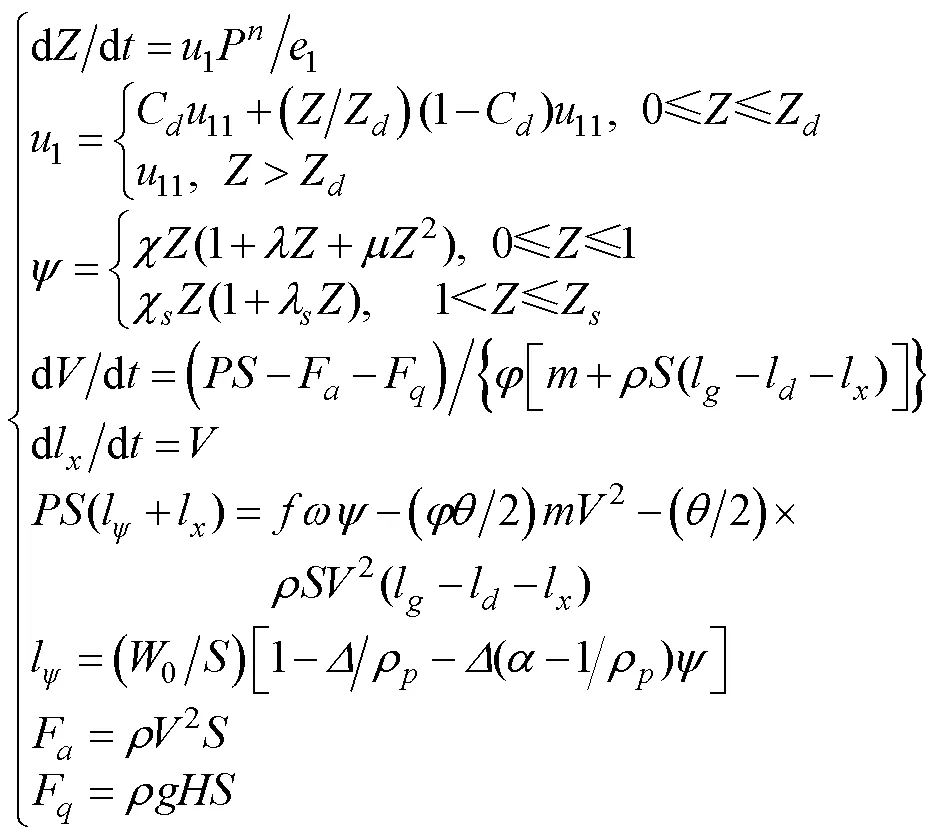

计算采用内弹道常用的四阶龙格-库塔法[7], 计算时输入火炮构造、弹丸诸元、装药条件和计算步长。其中初始变量:=1.0×105,=0,=0,=0。
1.3 参数优化
1.3.1 各因素影响规律
水下发射时弹丸前部充满水, 随着弹丸向炮口运动, 炮管内的水柱质量不断变化, 即膛内运动是一个变质量运动过程。优化之前, 首先分析各因素对内弹道参数的影响, 然后根据变化规律和工程实际给出参数计算范围。由于因素过多, 文中仅给出水深和身管长对内弹道参量的影响, 但也可看出水下发射与大气中发射的内弹道区别很大。
1) 水深对内弹道参数的影响
计算条件: 口径为30 mm, 发射药为高氮单基药, 药型为7孔圆柱形, 药弧厚为0.4 mm, 药量47 g, 容积55 mL, 弹丸行程长0.816 m。计算结果见表1, 可以看出, 随着水深的增加, 初速0呈变小趋势、最大膛压P呈增加趋势, 但对初速的影响很小, 在500 m水深初速减小不到1%, 对膛压的影响稍大一些, 在500 m水深膛压增大约7%。
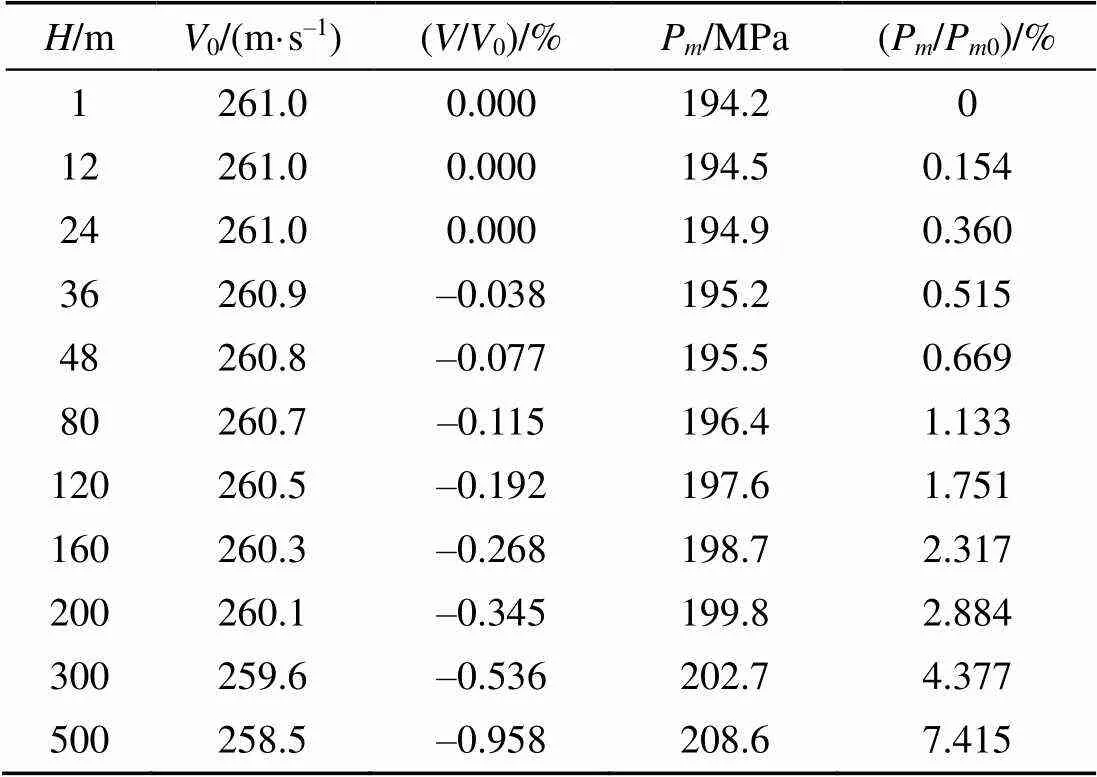
表1 水深对内弹道参数的影响
初速变化率(/0)是深度为12 m和24 m时相对于1 m时的降低率; 膛压变化率(P/P0)是深度为12 m和24 m时相对于1 m时初速的升高率。
除了法院调解再审的启动条件,其启动程序上的规则也同样不容忽视,尤其2012年民事诉讼法在再审管辖、再审期间及其起算点等方面均有调整,所以我们理应思考调解书的相关制度需要在多大程度上随之变动。
2) 身管长对内弹道参数的影响
计算条件同上, 水深为12 m, 计算曲线见图2~图5。从图2可以看出, 最大膛压P与身管长度L基本呈线性关系, 最大膛压随身管长度的增加单调递增; 而炮口初速0与身管长度为较为复杂的抛物线关系, 开始随身管长度的增加而增加, 但增加速率趋缓, 增加到某一长度时, 炮口初速呈下降趋势。
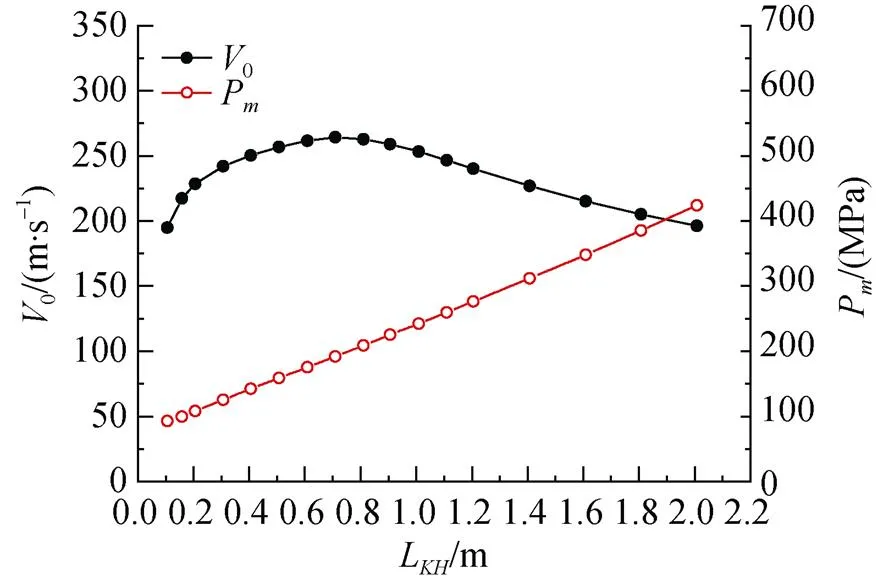
图2 身管长度对内弹道参数影响曲线
图3为身管长为2.3 m时弹丸运动速度与弹丸位移l的关系曲线, 可以看出, 弹丸速度在身管的后半段呈现下降趋势, 其原因为弹丸加速度在弹丸位移0.9 m处开始转为负值(见图4), 在弹丸头部出炮口时达到最小。
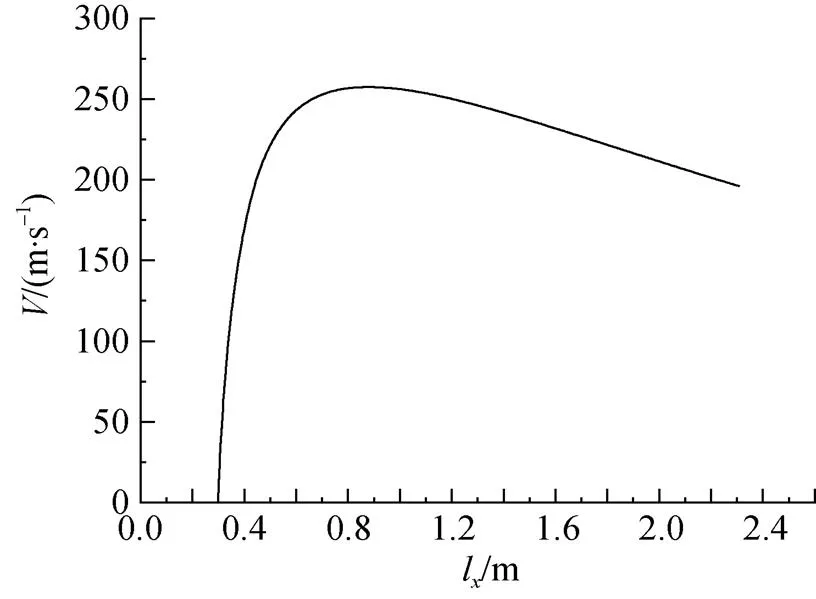
图3 身管长为2.3 m时弹丸运动速度与弹丸位移的关系曲线
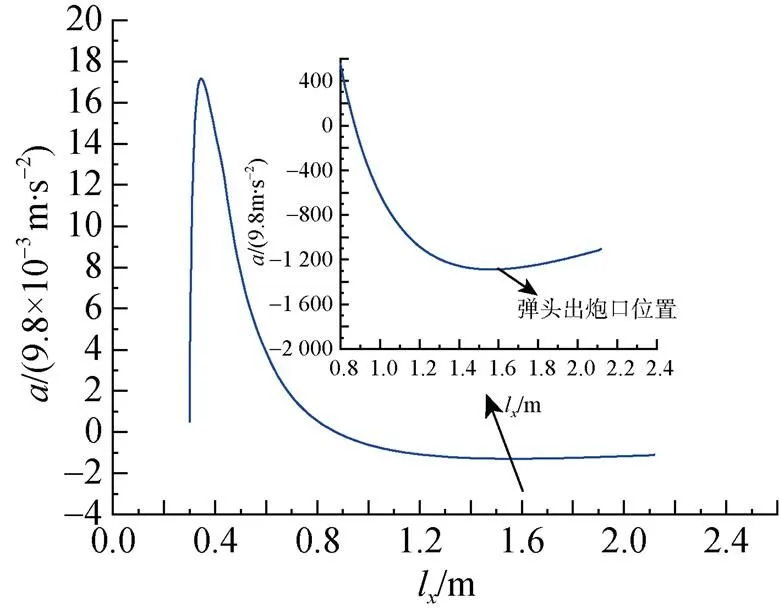
图4 身管长2.3 m时弹丸加速度与弹丸位移的关系曲线
1.3.2 设计变量及取值范围的确定

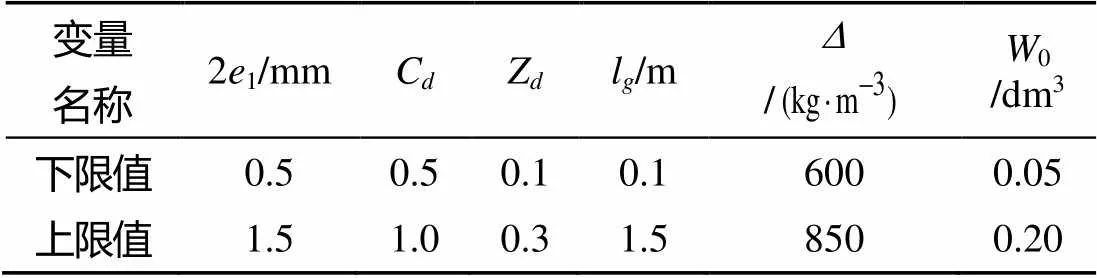
表2 设计变量及其取值范围
1.3.3 设计目标
根据对样品影响因素的分析, 找出最佳匹配, 即弹重0.256 kg, 弹丸长度0.1 m, 药室长度0.3 m,
水深12 m时, 出速0=300 m/s的技术方案, 其中要求最大膛压P、弹丸行程长l尽量小。根据设计参数的重要性选取权重, 计算中选取初速0、P、l权重值分别为10, 5, 2。
1.3.4 优化算法的选取
优化算法在内弹道设计方面的应用较广泛[8-11], 遗传算法是目前应用最为广泛、成功的探索型智能优化算法。在标准遗传算法基础上改进的众多算法之中, 大都借鉴生物界的自然选择和遗传, 多岛遗传算法为改进遗传算法中较常用的一种, 文中选用该算法进行动态加载试验装置优化设计。
多岛遗传算法每个种群被视为多个“岛”(子群), 在每个岛上并行地进行独立的选择、交叉、变异等标准遗传算法操作, 岛中个体采用轮盘赌选择法和精英保留相结合的策略, 周期性地随机选择一些个体进行迁移操作, 根据设置的迁移间隔和迁移率, 从一个岛上的子种群中选择个体迁移到另一个岛上, 并继续进行标准遗传算法操作, 迁移保持了样本的多样性, 提高了获得全局最优解的机会, 抑制早熟现象的发生。多岛遗传算法流程具体描述如下。
1) 初始化最大进化代数, 种群分散的岛数, 每个岛上随机生成个体作为各岛初始种群。
2) 计算各岛子种群的个体适应度。
3) 各岛并行进行独立选择、交叉、变异操作。
4) 运用轮盘赌法和精选保留相结合的迁移策略进行岛之间的信息交换, 得到新的岛。
5) 终止条件判断: 若不满足精度要求或最大进化代数要求, 则转向步骤2); 若满足终止要求, 则将具有最大适应度的个体作为最优解输出, 结束优化。
2 结果分析
优化模型参数设置如下: 种群数10, 岛数10, 代数60, 杂交概率1.0, 变异概率0.01, 迁徙概率0.01, 迁徙间隔5代。经过6 000次的迭代步数(run), 得到了药室容积、弧厚、装药量、燃速系数、钝感燃速修正系数的最佳组合, 在达到炮口初速要求的同时最大膛压和弹丸行程长度也较小。运用多岛遗传算法优化迭代过程如图6和图7所示。
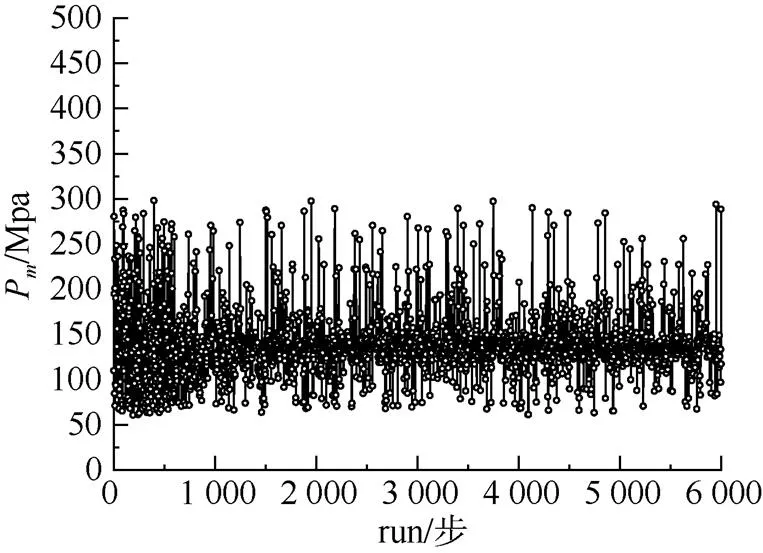
图6 最大膛压随迭代步数的变化曲线
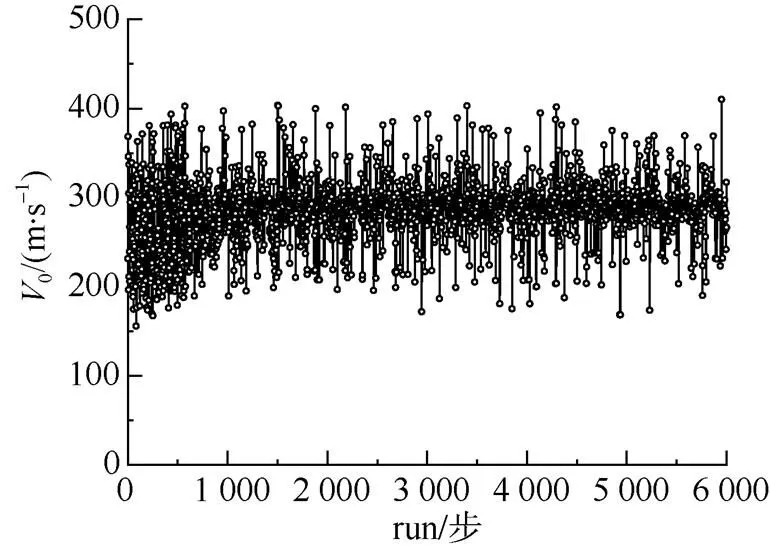
图7 炮口速度随迭代步数的变化曲线
从计算过程来看, 最大膛压P在0~700步时较分散, 700步后绝大部分计结果收敛于150 MPa附近。收敛过程中, 算法所执行的变异操作偶尔出现震荡, 但并不影响优化结果的收敛性; 在整个计算过程中炮口初速主要集中于200~400 m/s间, 由于计算步数较多, 符合要求的计算结果反复出现达百次之多, 设计变量参数变化幅值很小, 计算结果稳定。优化结果见表3, 可知在实现初速的情况, 优化参数都在常用易加工范围内, 工程上易实现。

表3 优化计算结果
3 结束语
由于水下全浸没式发射过程的影响因素更多、变化趋势更为复杂, 有些变化规律甚至与陆炮相反。例如在陆炮设计时, 增加身管长度是增加弹丸出炮口速度的技术措施, 而水下发射身管长度的增加, 弹丸初速并不一定增加甚至可能减小, 这些变化使得采用一般的设计方法难以确定最优方案。文中综合考虑钝感发射药、弹丸对身管内弹丸水柱的做功、炮口喷出水阻以及水深的影响等诸多因素, 采用优化设计方法快速地得到较为合理的参数组合, 满足设计的技术指标, 大幅度减小内弹道设计的工作量, 可为后期水下内弹道工程化设计提供参考。
[1] 孔德仁, 王昌明, 柳光辽, 等. 水下枪械内弹道基本方程组及其设计[J]. 南京理工大学学报, 1996, 23(3): 197- 200.
Kong De-ren, Wang Chang-ming, Liu Guang-liao, et al. Fundamental Equations of Underwater Gun’s Interior Trajectory and It’s Design[J]. Journal of Nanjing University of Science and Technology, 1996, 23(3): 197-200.
[2] 姚养无, 张海燕, 徐礼. 水下枪械内弹道基本方程组[J].火炮发射与控制学报, 2006(1): 6-9.
Yao Yang-wu, Zhang Hai-yan, Xu Li. Fundamental Equations for Interior Ballistic of Underwater Gun[J]. Journal of Gun Launch & Control, 2006(1): 6-9.
[3] 程兆刚, 曹洪娜, 韩保红. 水下枪械弹丸膛内速度变化规律的研究[J]. 机械与电子, 2010(7): 77-78.
[4] 兰晓龙. 水下枪械发射内弹道研究[D]. 太原: 中北大学, 2014.
[5] 刘双杰, 郝永平. 35 mm高射炮钝感发射药的内弹道仿真[J]. 弹箭与制导学报, 2010, 30(1): 43-46.
Liu Shuan-jie, Hao Yong-ping. Numerical Simulation of Interior Ballistic for 35 mm Antiaircraft Artillery with Deterred propellant[J]. Journal of Projectiles Rockets Missiles and Guidance, 2010, 30(1): 43-46.
[6] 李杰. 钝感发射装药弹道分析[J]. 火炮发射与控制学报, 1997(2): 17-22.
[7] 张小兵. 枪炮内弹道学[M]. 北京: 北京理工大学出版社, 2014.
[8] 王敬. 基于方案满意度的火炮内弹道优化设计[J]. 弹箭与制导学报, 2011, 31(4): 133-135.
Wang Jing. An Optimal Design Based on Satisfactory Degree of Gun’s Interior Ballistics[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(4): 133- 135.
[9] 李炜. 埋头弹火炮内弹道优化设计及数值模拟[D]. 南京: 南京理工大学, 2013.
[10] 李克婧, 张小兵. 混合装药内弹道性能优化及应用[J].火炸药学报, 2011, 34(6): 74-79.
Li Ke-jing, Zhang Xiao-bing. Optimization and Application of Interior Ballistic Performance with Mixed-charge [J]. Chinese Journal of Explosives & Propellants, 2011, 34(6): 74-79.
[11] 张泽峰, 傅建平, 曹营修, 等. 基于改进差分进化算法的内弹道参数优化[J]. 火力与指挥控制, 2017, 42(7): 1182-1185.
Zhang Ze-feng, Fu Jian-ping, Cao Ying-xiu, et al. Interior Ballistic Parameter Optimization Based on Improved Differential Evolution Algorithm[J]. Fire Control & Command Control, 2017, 42(7): 1182-1185.
Optimization Design of Interior Trajectory Parameters of Fully-Immersed Artillery
GUO Ying-hua, LI Rui-jing, LIU Wei, DONG Yan-cheng
(Northwest Institute of Mechanical and Electrical Engineering, Xianyang 712000, China)
The interior trajectory optimization design of underwater artillery has become an active topic in underwater attack and defense research owing to the increasing threat to underwater security. The launching process of artillery in water is more complicated than that in the air environment, especially regarding small-caliber artillery in the presence of a variable burning rate propellant. In this study, the optimization design of internal ballistic parameters is conducted using a multi-island genetic algorithm, based on the classical interior ballistic model, to investigate the launching process of fully immersed artillery. Some parameters such as the insensitive propellant, work of a projectile on the water column in a barrel, water resistance of the muzzle, and the influence of water depth are considered to establish the interior ballistic equations. The loading and propellant parameters, such as chamber volume, projectile travel length, propellant web size, insensitive depth, surface burning rate coefficient correction, and mass of charge, are set to achieve the maximum bore pressure and muzzle velocity. Engineering analysis of the optimization results shows that the proposed method can quickly achieve reasonable parameter indicators to greatly reduce the workload of interior trajectory design.
fully immersed artillery; interior trajectory; underwater launch; optimization design; multi-island genetic algorithm
郭映华, 李瑞静, 刘伟, 等. 全浸式火炮内弹道参数优化设计[J]. 水下无人系统学报, 2021, 29(5): 616-620.
TJ63; TJ302
A
2096-3920(2021)05-0616-05
10.11993/j.issn.2096-3920.2021.05.015
2020-11-10;
2021-02-24.
郭映华(1972-), 男, 硕士, 研究员, 主要研究方向为内弹道与装药结构设计.
(责任编辑: 杨力军)
