鱼雷爆炸作用下潜艇鞭状运动响应仿真分析
2021-11-08郭志荣陆文俊金晓宇
郭志荣, 陆文俊, 金晓宇
鱼雷爆炸作用下潜艇鞭状运动响应仿真分析
郭志荣, 陆文俊, 金晓宇
(海军士官学校 兵器系, 安徽 蚌埠, 233012)
为了提高鱼雷水下近场爆炸对潜艇的毁伤效果, 分析爆炸载荷作用下潜艇结构鞭状运动响应规律,文中从能量叠加关系出发, 将爆炸载荷按时间顺序分解为冲击波载荷、气泡脉动载荷和气泡低压载荷3个阶段。建立单质点弹簧系统, 分析三阶段载荷与潜艇结构振动之间的能量叠加关系, 并基于对载荷的分析, 对不同能量结构的潜艇结构鞭状运动响应进行仿真。仿真结果与试验数据吻合较好, 说明单质点弹簧系统能够定性描述鱼雷在潜艇中部近水场爆炸时, 潜艇结构鞭状运动的能量叠加关系。文中工作可为分析鱼雷近场水下爆炸载荷作用下的潜艇结构鞭状运动毁伤效果提供理论依据。
鱼雷; 潜艇; 水下爆炸; 鞭状运动; 单质点弹簧系统
0 引言
鱼雷攻击潜艇发生近场水下爆炸, 在特定的工况下, 气泡脉动载荷诱发的鞭状运动会危及潜艇的总体强度, 甚至直接将其折断[1-2]。圆柱壳作为潜艇典型的结构形式, 因其在水下爆炸作用下的载荷及毁伤特性一直受到学者们的关注[3]。李玉节等[4]针对船体梁模型, 在计算船体鞭状运动时考虑剪切变形的影响, 在弹性范围内与实验结果吻合较好。宗智等[5-7]在此基础上考虑塑性变形的影响, 采用刚塑性理论求解鞭装响应过程中塑性变形起主导作用的中间时期, 分析了潜艇在水下爆炸载荷下的鞭状运动特性。董海等[8]将船体梁模型和双重渐近近似法结合在一起, 采用变截面梁模型计算结构响应, 而用双重渐近近似法计算流体载荷, 对结构的时域和频域响应均进行了深入的分析。在实验研究方面, Brett等[9]对水中圆柱壳进行了小当量水下爆炸试验, 得到近场爆炸载荷作用下圆柱壳动响应, 发现气泡载荷的作用大于冲击波载荷; 2008年其又采用试验与数值方法, 开展了圆壳柱在水下爆炸载荷作用下的毁伤特性研究, 分析了气泡与结构相互作用及气泡载荷对圆柱壳的冲击毁伤影响[10]。朱锡等[11-12]分别通过缩比模型实验研究了水面舰艇在水下爆炸作用下的鞭状运动响应, 发现气泡作用是结构产生严重总体破坏的主要因素。黄晓明等[13]针对圆壳柱水下爆炸鞭状响应进行试验研究, 发现圆壳柱响应分为气泡滞后流引起的刚体运动和1阶垂向运动为主的弹性振动两部分。汪浩等[14]基于MSC/Dytran研究了水下爆炸气泡作用下内加强筋圆柱壳结构毁伤机理, 并探讨了结构参数、药包位置等变量对结构变形及毁伤模式的影响。
已有的文献对潜艇结构的毁伤特性, 多是按照物理性质将水下爆炸载荷分解为冲击波载荷与气泡载荷两部分。冲击波载荷用经验公式来描述[15], 由于其时间作用非常短, 已有研究多认为其对结构整体响应贡献较小而加以忽略。而实际上, 冲击波作用后结构的响应状态应为气泡脉动阶段结构响应的初始值, 能否忽略冲击波对结构的影响, 具体误差如何尚待研究。气泡载荷结构对整体响应的研究多采用气泡动力学公式来描述, 使用较多的是Vernon气泡模型[16], 其可控的主要变量为药量与距离。但当药量改变后, 载荷的强度与频率同时改变, 气泡动力学模型没有指出影响结构响应叠加效果的主要因素。针对此, 文中按照时间顺序, 对水下爆炸一个气泡脉动周期内的载荷进行分解与描述, 引入不同能量输出结构中的冲击波能和气泡能, 采用单质点弹簧系统替代气泡动力学模型, 来分析三阶段载荷与潜艇结构振动之间的能量叠加关系, 为分析鱼雷近场水下爆炸载荷作用下的潜艇结构鞭状运动毁伤效果提供理论依据。
1 载荷分解与描述
典型的水下爆炸中某一点处的自由场压力曲线如图1所示。对于气泡脉动一个周期内的载荷, 按照其特征和时间顺序可分为3个阶段。第1阶段, 主要描述了压力方向为正的初始阶段载荷, 与传统的冲击波载荷不同, 文中定义的第1阶段载荷不但包含了冲击波载荷, 还包含了爆炸气泡初始膨胀时的辐射压力。由于精确计算载荷何时降至0值较为复杂, 且意义不大, 作为一种简化处理, 取水下爆炸气泡第1个脉动周期的前10%作为第1阶段载荷, 称为冲击波阶段载荷。第2阶段, 是幅值较小但压力方向为负的气泡低压载荷阶段, 其时间范围为0.1~0.9周期。第3阶段为气泡脉动载荷阶段, 其时间范围为0.9~1.1周期。
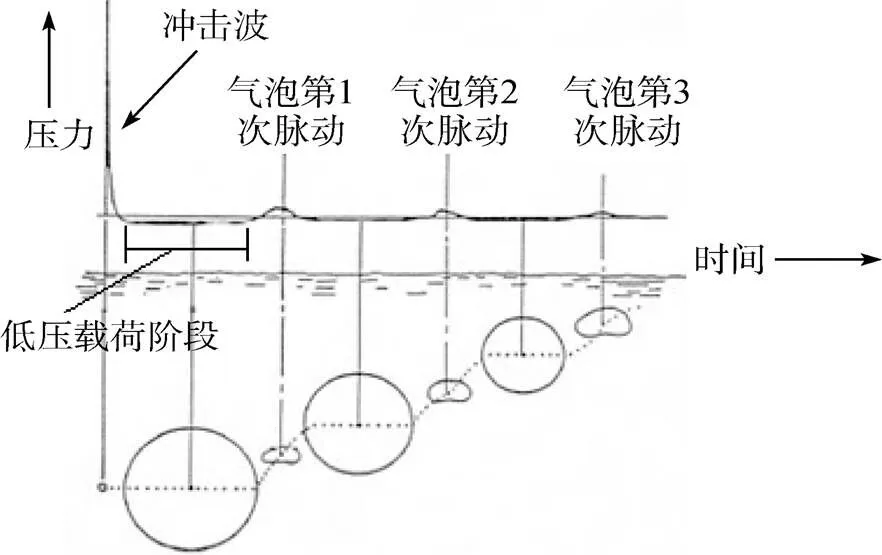
图1 水下爆炸载荷特性示意图
水下爆炸现象传统上被视为2个似乎并不相干的过程: 冲击波过程和气泡过程, 这使得气泡过程初始条件的选取较为困难。Thomas等[15]将2个阶段处理为同一个物理现象, 第1个阶段为第2个阶段提供初始条件。
定义水下爆炸作用下流场中某点处的Geers- Hunter载荷曲线为

式中:为爆炸药量;为测点距爆心的距离;为爆心处水深。
根据Geers-Hunter载荷函数载荷分段分解方法, 对于气泡脉动1个周期内的载荷, 引入冲击波能当量和气泡能当量, 则可得到能够表达不同能量输出结构特性的水下爆炸载荷函数
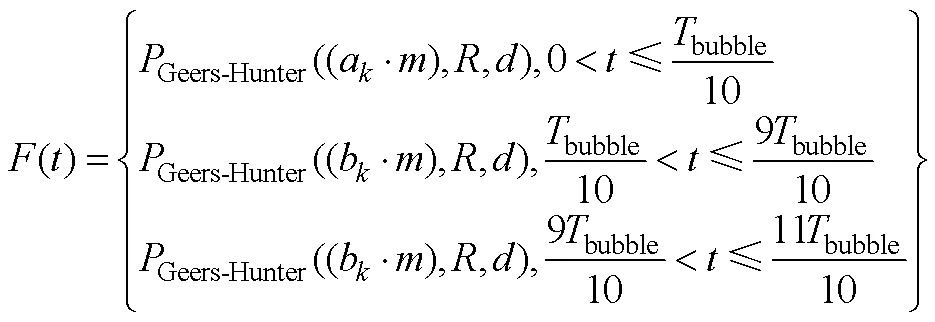
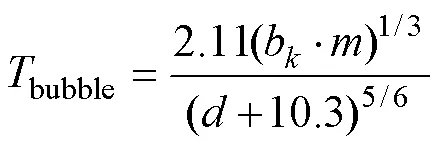
式中:Geers-Hunter为载荷函数;a为冲击波能当量系数;b为气泡能当量系数;为爆炸药量;bubble为炸药爆炸气泡的脉动周期;为爆深。
2 典型水下整体结构鞭状运动响应仿真
为验证仿真结果, 设计了试验方法与仿真结果进行对比。耐压壳体是潜艇结构中最重要的部分, 也是决定潜艇结构低阶固有频率的主要结构。文中以某型潜艇耐压壳为原型, 采用加肋圆柱壳形式, 建立潜艇结构试验模型, 按照能够反映潜艇结构振动基本特性和频率相似的原则进行模型设计。试验模型的设计目标是其垂向1阶湿模态频率在14~31.5 Hz范围内, 试验模型参数见表1。沿模型长度方向布置了10个纵向应变测点, 测点布置如图2所示。

表1 圆柱壳体试验模型设计参数

图 2 应变测点布置图
试验药量为10 g TNT, 药包爆炸位置均位于模型中部, 爆距为1.0 m。在该距离上可以忽略气泡低压载荷对结构的影响, 仅考虑冲击波阶段载荷和气泡脉动载荷造成的结构整体响应。
使用球面波假设, 将冲击波阶段载荷和气泡一次脉动载荷作为流体压力载荷输入到软件中。ABAQUS软件的流固耦合为声固耦合, 即将流体视为声学单元, 其流固耦合理论方程参见式(4), 软件按照散射波公式最终将流体载荷计算成结构受力。有限元模型及球面波加载示意如图3所示。
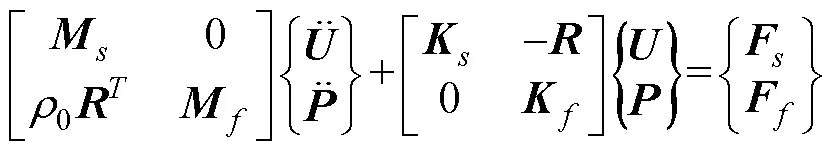
式中: M, K和F分别为质量矩阵、刚度矩阵和载荷矩阵,下标s代表结构, f代表流体; R为流固耦合矩阵, 代表流固耦合界面上每个节点处的有效面积, 它将界面上的流体压力转换成结构所受载荷; 为流体密度; U和P分别代表节点位移矩阵和流体声学压力矩阵。
由图4可见, 在模型振动1个半周期(100 ms)内, 计算值与试验值吻合较好, 特别是点与点处的应变峰值误差较小,点应变峰值略有差别, 主要是由于计算中忽略了气泡低压载荷部分; 在100 ms之后应变曲线相差较大, 主要是由于试验中, 模型振动受水的阻尼作用而衰减, 但在仿真计算中没有考虑阻尼的影响。在1.0 m爆距下, 忽略气泡低压载荷的结果是可以接受的。使用分解的冲击波阶段载荷和气泡脉动载荷对10 g TNT炸药爆距1.0 m时的模型仿真计算, 能够准确反映结构响应过程。

图4 模型中部纵向应变计算结果与试验结果比较曲线
保持药量与爆距不变, 人为改变气泡载荷出现的时间, 即人为指定bubble时间, 计算气泡脉动的加载时间对响应结果的影响。计算结果见图5及表2。
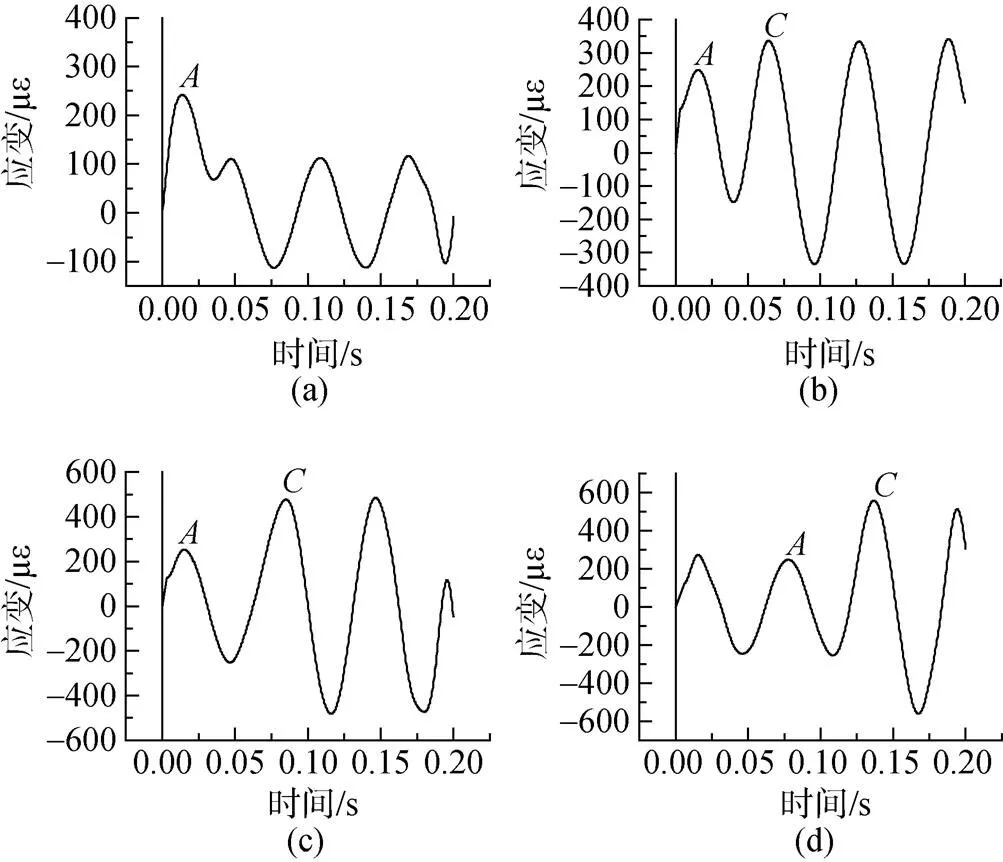
图5 不同气泡脉动加载时间应变曲线
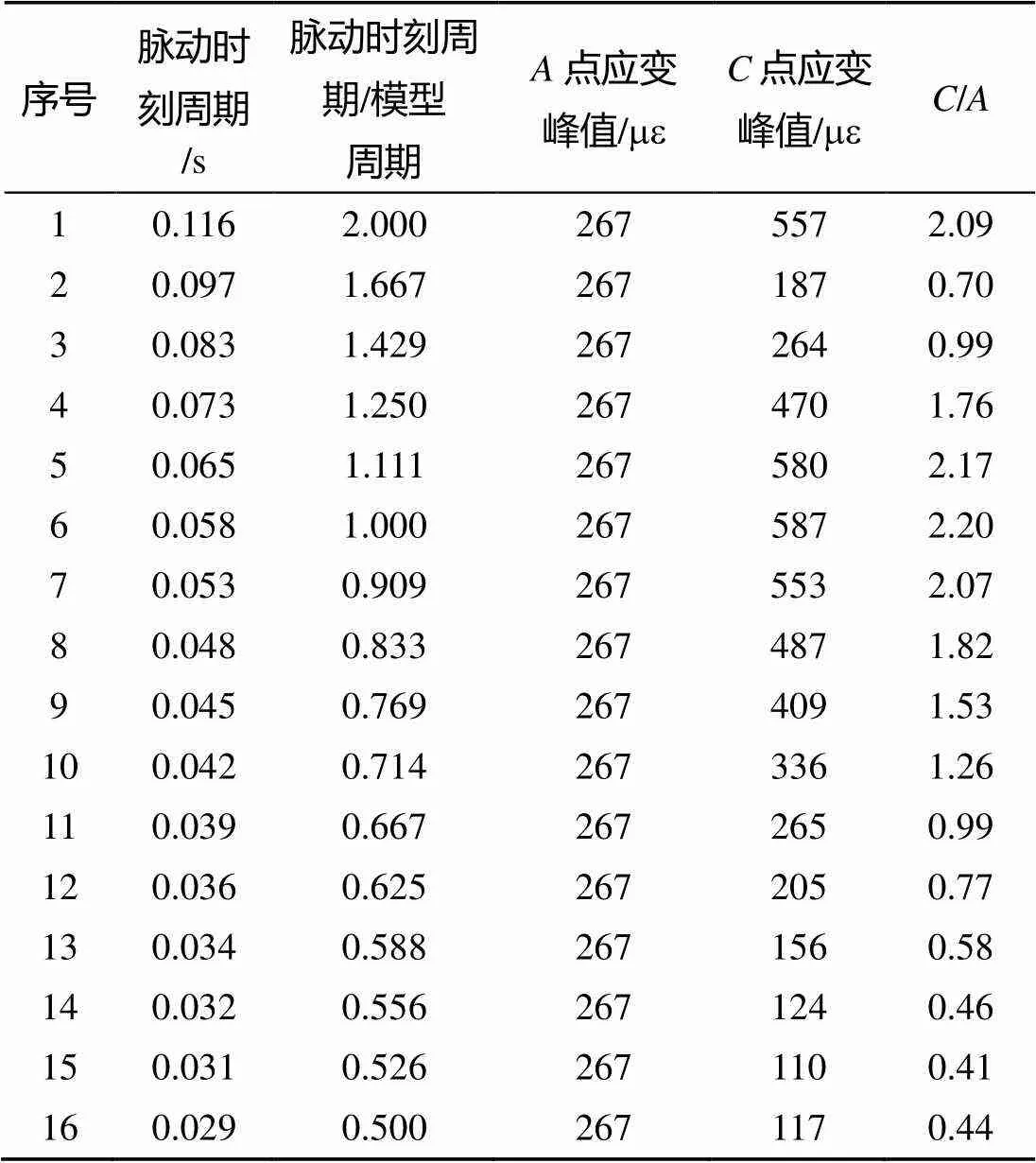
表2 不同气泡脉动加载时间应变仿真结果
由图5及表2可见, 气泡脉动载荷的加载时间对响应结果有着十分显著的影响。当气泡脉动载荷介于模型1阶垂向振动的3/4~5/4周期内, 初始振动均得到了增强, 应变峰值增大(/的数值大于1), 其气泡脉动载荷发生在模型固有振动的1个整周期(58 ms)时, 脉动载荷与初始振动的叠加效果最大, 其后振动的应变峰值也最大。当气泡脉动载荷介于模型1阶垂向振动的1/4~3/4周期内时, 初始振动受到了削弱, 其后模型振动的应变峰值降低(/的数值小于1)。值得说明的是, 实际计算中1/2周期的点的应变峰值略有变化, 这是由于对信号作滤波处理的影响。由于冲击波阶段载荷没有改变, 因此表2中将点峰值统一为267 με。
3 能量叠加简化模型
参考上节的仿真结果, 文中研究鱼雷在潜艇中底部爆炸可等同为炸药在细长船体结构中底部爆炸的情况, 其整体响应主要为1阶垂向振动, 因此可用模型中点处的运动来描述整个模型的运动状态, 进而使用1个质点弹簧系统来定性的描述不同阶段载荷对结构振动的能量叠加关系。
质点弹簧系统如图6(a)所示, 则质点在初始脉冲载荷作用下的运动如图6(b)所示, 为一个正弦曲线。暂时不考虑质点的质量与弹簧的刚度, 仅将质点振动的频率设为潜艇结构的1阶湿模态振动频率, 则质点的振动与鱼雷水下爆炸作用下结构模型中部测点的应变曲线对应(参见图4)。
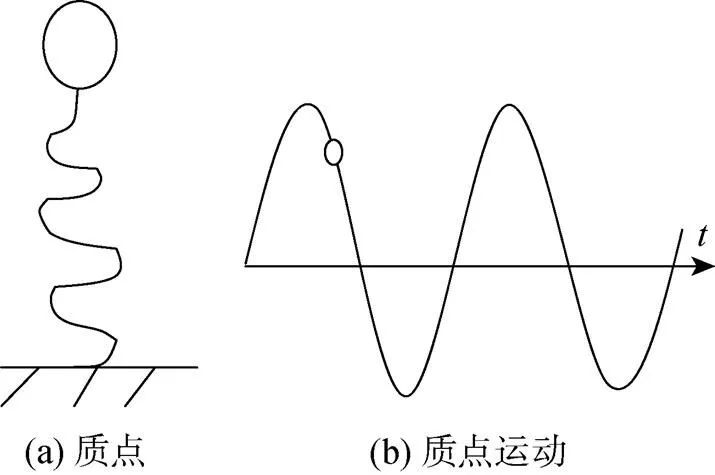
图6 质点弹簧系统及质点运动示意图
初始冲击波阶段载荷赋予整个系统1个初始的动能, 质点开始按照其固有频率作往复振动, 振幅的大小体现了冲击波阶段载荷作用的效果。在振动过程中, 系统的动能与势能相互转化, 在振动峰值处, 势能最大, 动能为零; 在平衡位置时, 动能最大, 势能为零。气泡脉动载荷能量与质点弹簧系统能量可能产生叠加, 造成其后振动幅值的增加, 也可能相互抵消, 造成振动幅值的减弱。能量的叠加或抵消取决于气泡脉动载荷作用时, 质点的运动速度方向与载荷方向为同向或反向。两者同向时, 能量叠加; 两者反向时, 能量抵消。
能量叠加或抵消的程度取决于系统动能的大小, 即质点速度的大小, 速度越大, 叠加或抵消的程度越大; 动能越小, 能量叠加或抵消的程度越小。由于气泡脉动载荷为脉冲载荷, 其方向与造成系统开始振动的冲击波阶段载荷的方向始终一致(如图7), 则对于系统而言发生能量抵消的区间为1/4~3/4周期, 发生能量叠加的区间为3/4~5/4周期, 在平衡位置时系统的动能最大, 则能量叠加与抵消的效果也最好。
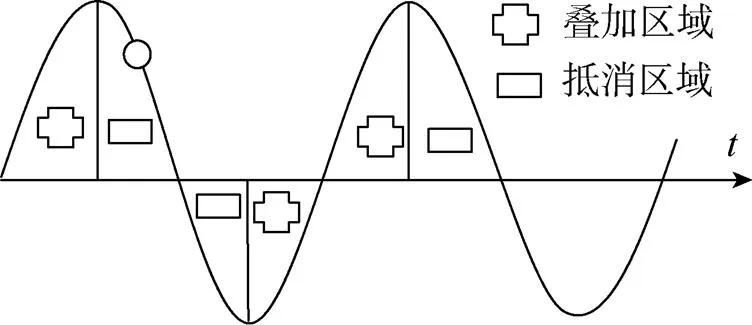
图 7 气泡脉动载荷与初始振动的能量叠加与抵消区间
4 质点弹簧系统仿真分析
4.1 冲击波能当量的影响
保持周期和气泡载荷不变, 研究冲击波能当量对响应的影响, 计算结果见表3(如图4所示、、点的位置)。计算结果用质点弹簧的系统模型可以得到合理的解释, 冲击波能越大, 则造成的初始振动的能量越大,点的应变峰值也越高, 在气泡脉动载荷的强度与时间不变时, 相应的最大应变峰值也越高。同时由于冲击波能量的增加, 其与气泡能的比值也增加, 则叠加关系不变时, 最终/的比值则有所减小。可见冲击波阶段载荷对于结构整体响应的影响是不可忽视的, 其赋予系统的初始能量作为整个响应的基础, 对最大响应峰值的影响是直接的。
表3中第1行代表了冲击波能量为0时, 单独脉动载荷造成的应变峰值为374 με。与冲击波阶段载荷造成的初始振动应变峰值267 με比较可见, 单独气泡脉动造成的模型振动峰值比单独冲击波阶段载荷造成的模型振动峰值稍大, 但仍处于同一量级。由此可见, 二者之间的叠加关系对于结构响应峰值的影响至关重要。
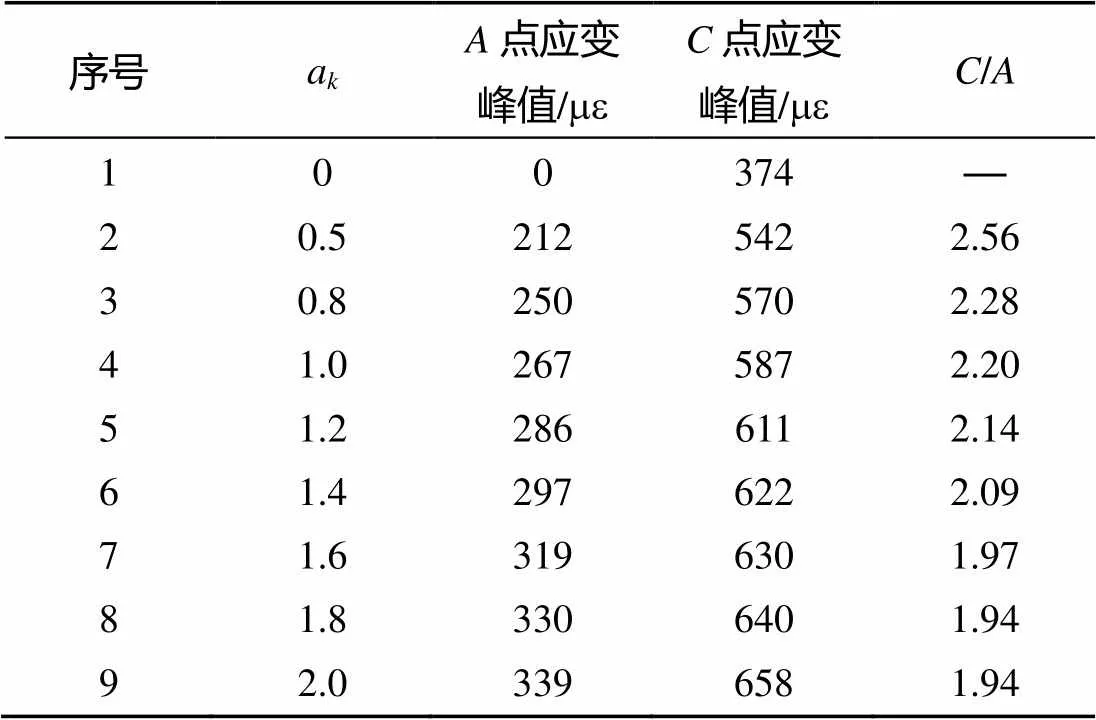
表3 不同冲击波能当量应变仿真结果
4.2 气泡能当量的影响
改变气泡能当量, 考察气泡能当量对计算结果的影响, 计算结果见表4。

表4 不同气泡能当量应变仿真结果
表4的计算结果也可以用质点弹簧的系统模型来进行解释, 冲击波能不变, 则初始振动的能量也不变, 气泡脉动载荷作用的时间不变, 则叠加关系也变化较小, 当气泡能增加时, 相应最大应变峰值也越高。同时由于气泡能量的增加, 其与冲击波能量的比值也增加, 则叠加关系不变时, 最终的/比值增大。
使用基于时间分解的载荷对加筋圆柱壳模型在水下爆炸作用下的整体响应仿真表明, 单独冲击波阶段载荷与气泡脉动载荷造成的结构整体响应应变峰值在同一量级, 影响响应结果的关键因素是两阶段载荷的能量叠加关系, 这种叠加关系可以使用单质点弹簧系统来定性描述。
4.3 气泡低压载荷的影响
使用同样的方法对10 g TNT在水中1.5 m深处, 距模型0.5 m爆距时的工况进行仿真计算, 当载荷仅考虑冲击波阶段载荷和气泡脉动载荷时, 所得结果与试验结果的对比如图8所示。由图可见, 仿真结果与试验结果的差异主要在于点的峰值仿真结果略大于试验结果,点与点应变峰值仿真结果明显小于试验结果。
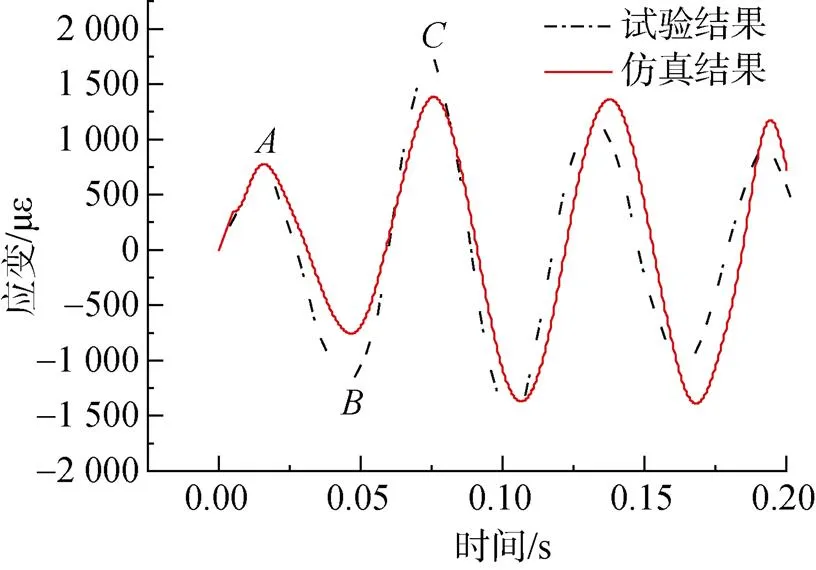
图8 未考虑气泡低压载荷时模型中部纵向应变仿真曲线
采用质点弹簧系统模型来分析, 可见在试验中, 冲击波载荷作用后, 气泡脉动载荷发生前, 系统的能量得到了增强, 体现在点的应变峰值较点增加较多。这段时间内的载荷只能为气泡低压载荷, 可见对于0.5 m爆距工况, 气泡低压载荷的影响不能忽略。
使用式(2)中的低压阶段载荷计算方法得到10 g TNT在水中1.5 m处, 0.5 m爆距工况时的气泡低压载如图9所示。加入低压载荷后该工况的仿真计算结果如图10所示。可见, 加入低压载荷后, 仿真计算结果与试验结果在第1.5个周期内吻合良好, 由于爆距近、响应强, 模型振动在1.5个周期后的衰减十分强烈。在该工况下, 对于1.5个周期后的结构响应, 必须考虑阻尼的影响。

图9 10 g TNT 0.5 m爆距时的气泡低压载荷
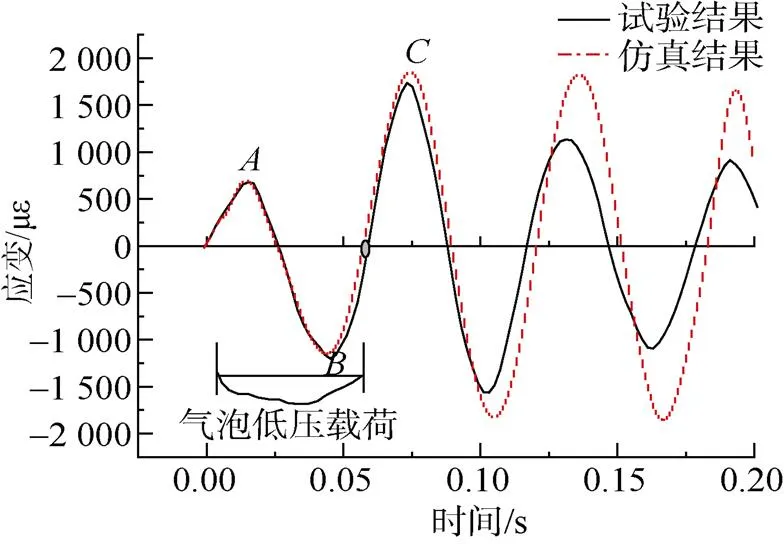
图10 考虑气泡低压载荷时模型中部纵向应变仿真曲线
图9中, 低压载荷方向为负, 其压力值为中间大, 两端小, 基本上相对于气泡最大半径时刻对称。气泡最大半径时刻为28 ms处, 接近模型振动的1/2周期点, 将气泡低压载荷作用时间标于图10中, 可知在前1/4周期时间内存在能量抵消, 因而点的应变峰值较未加入时小。从总的效果看, 在前1/4和后1/4周期的能量抵消区内, 低压载荷幅值较小, 而在1/4~3/4周期的能量叠加区内, 低压载荷幅值较大, 因此, 总的效果体现为能量的叠加。加入低压载荷后的点应变峰值1 785 με大于未加入低压载荷的应变峰值1 348 με。
使用质点弹簧系统具体分析气泡低压载荷对系统能量的影响, 由于气泡低压载荷的作用方向与冲击波阶段载荷相反, 因此其与系统初始振动的叠加区间也与气泡脉动载荷相反, 如图11所示。并且气泡低压载荷的作用时间较长, 因而在其整个作用时间内既经历了与系统能量的叠加, 也经历了能量的抵消过程。对于最终总能量的影响, 则需要具体分析。

图11 气泡低压载荷与系统能量叠加与抵消区间分布
5 结束语
文中从能量叠加关系出发, 将鱼雷水下爆炸载荷按时间顺序分解为冲击波阶段载荷、气泡低压载荷及气泡脉动载荷3个阶段。基于载荷的分解, 建立了单质点弹簧系统来定性描述3阶段载荷与潜艇结构鞭状运动间的能量叠加关系, 该方法能够描述不同能量结构的整体响应, 模型试验验证了仿真计算的准确性, 为分析鱼雷近场水下爆炸载荷作用下的潜艇结构鞭状运动毁伤效果提供理论依据, 对提高鱼雷对潜艇的毁伤效果提供了理论指导与方法保障。但文中对鞭状运动的最优求解问题目前仍停留在线弹性范围内, 同时只有细长梁在中部爆炸工况下才适合用质点弹簧的运动来模拟模型中部的运动, 质点质量、弹簧刚度以及各阶段载荷对系统等问题都有待进一步研究给出精确的数学描述。同时, 如何将鞭状运动的最优求解扩展到塑性范围, 以及进一步考虑材料的应变率效应和系统的阻尼等对鞭状运动运动响应的影响, 都值得作进一步的深入分析。
[1] 鲁忠宝, 黎勤, 哈海荣. 不同能量输出结构战斗部水下爆炸毁伤威力试验研究[J]. 水下无人系统学报, 2019, 27(1): 71-77.
Lu Zhong-bao, Li Qin, Ha Hai-rong. Experimental Study on Underwater Explosion Damage Power of Warhead with Different Energy Output Configuration[J]. Journal of Un- manned Undersea Systems, 2019, 27(1): 71-77.
[2] 金键, 朱锡, 侯海量, 等. 水下爆炸载荷下舰船响应与毁伤研究综述[J]. 水下无人系统学报, 2017, 25(6): 396-409.
Jin Jian, Zhu Xi, Hou Hai-liang, et al. Review of Dynamic Response and Damage Mechanism of Ship Structure Subjected to Underwater Explosion load[J]. Journal of Un- manned Undersea Systems, 2017, 25(6): 396-409.
[3] 鲁忠宝, 黎勤. 鱼雷战斗部装药特点与发展[J]. 水下无人系统学报, 2018, 26(1): 10-15.
Lu Zhong-bao, Li Qin. Research on Charge in Torpedo Warhead[J]. Journal of Unmanned Undersea Systems, 2018, 26(1): 10-15.
[4] 李玉节, 潘建强, 李国华, 等. 水下爆炸气泡诱发舰船鞭状效应的实验研究[J]. 船舶力学, 2001, 6(5): 75-84.
Li Yu-jie, Pan Jian-qiang, Li Guo-hua, et al. Experimental Study of Ship Whipping Induced by Underwater Explosive Bubble[J]. Journal of Ship Mechanics, 2001, 6(5): 75-84.
[5] Zong Z. Dynamic Plastic Response of a Submerged Free- free Beam to an Underwater Gas Bubble[J]. Acta Mech- anics, 2003, 161: 179-214.
[6] Zong Z. A Hydroplastic Analysis of a Free-free Beam Floating on Water Subjected to an Underwater Bubble[J]. Journal of Fluids and Structure, 2005, 20: 359-372.
[7] 张弩, 宗智. 水下爆炸气泡载荷对舰船的总体毁伤研究[J]. 中国造船, 2012, 53(3): 28-39.
Zhang Nu, Zong Zhi. Global Damage of Ship Hull Subjected To Underwater Explosion Bubble Loading[J]. Ship- building of China, 2012, 53(3): 28-39.
[8] 董海, 刘建湖, 吴有生. 水下爆炸气泡脉动作用下细长加筋圆柱壳的鞭状响应分析[J]. 船舶力学, 2007, 11(2): 250-258.
Dong Hai, Liu Jian-hu, Wu You-sheng. Whipping Response Analysis of Slender Stiffened Cylindrical Shell Subjected to Underwater Explosion with Bubble Pulse[J]. Journal of Ship Mechanics, 2007, 11(2): 250-258.
[9] Brett J M, Yiannakopolous G, Schaaf P J V D. Timeresol- ved Measurement of the Deformation of Submerged Cylinders Subjected to Loading from a Nearby Explosion[J]. International Journal of Impact Engineering, 2000, 24(9): 875-890.
[10] Brett J M, Yiannakopolous G. A Study of Explosive Effects in Close Proximity to a Submerged Cylinder[J]. International Journal of Impact Engineering, 2008, 35(4): 206- 225.
[11] 朱锡, 李海涛, 牟金磊, 等. 水下近距爆炸作用下船体梁的动态响应特性[J]. 高压物理学报, 2010, 24(5): 343- 350.
Zhu Xi, Li Hai-tao, Mou Jin-lei, et al. Dynamic Response Characteristics of Ship-Like Beam Subjected to Underwa- ter Explosion in Near Field[J]. Chinese Journal of High Pressure Physics, 2010, 24(5): 343-350.
[12] 黄晓明, 朱锡, 牟金磊, 等. 近距水下爆炸作用下箱形梁模型中垂破坏实验研究[J]. 振动与冲击, 2011, 30(2): 19-23.
Huang Xiao-ming, Zhu Xi, Mou Jin-lei, et al. Experimental Study on Sagging Damage of Box-beam Model Subject to Close Range Underwater Exploration[J]. Vibration and Shock, 2011, 30(2): 19-23.
[13] 黄晓明, 朱锡, 牟金磊, 等. 圆壳柱在水下爆炸作用下鞭装响应试验研究[J]. 哈尔滨工程大学学报, 2010, 31 (10): 1278-1285.
Huang Xiao-ming, Zhu Xi, Mou Jin-lei, et al. Study on Whipping Response of Cylindrical Shell Under Underwater Explosion[J]. Journal of Harbin Engineering University, 2010, 31(10): 1278-1285.
[14] 汪浩, 王先洲, 刘均, 等. 水下爆炸气泡对内加筋圆柱壳结构毁伤机理分析[J]. 噪声与振动控制, 2016, 6: 111-116.
Wang Hao, Wang Xian-zhou, Liu Jun, et al. Damage Me- chanism Analysis of Inner-stiffened Cylindrical Shell Sub- jected to Underwater Explosion Bubble[J]. Noise and Vibration Control, 2016, 6: 111-116.
[15] Thomas L G, Kendall S Hunter. An Integrated Wave- Effects Model for an Underwater Explosion Bubble[J]. Jour- nal of the Acoustical Society of America, 2002, 111(4): 1584-1601.
[16] 李健, 荣吉利, 杨荣杰, 等. 水中爆炸冲击波传播与气泡脉动的实验及数值模拟[J]. 兵工学报, 2008, 29(12): 1437-1443.
Li Jian , Rong Ji-li, Yang Rong-jie, et al. Experiment and Numerical Simulation of Shock Wave Propagation and Bubble Impulse of Underwater Explosion[J]. Acta Armamentarii, 2008, 29(12): 1437-1443.
Simulation Analysis of the Whipping Response of a Submarine Subjected to the Torpedo Explosion
GUOZhi-rong, LU Wen-jun, JIN Xiao-yu
(Department of Weaponry Engineering, Naval Petty Officer Academy, Bengbu 233012, China)
To improve the damaging effect of a near-field underwater explosion caused by a torpedo on a submarine, the whipping response law of a submarine structure under an explosive load is analyzed. In this study, based on the energy superposition relationship, the explosive load can be divided into three stages: shock wave stage load, bubble pulsating load, and bubble low-pressure load; these can be arranged according to the explosive levels. The particle-spring system is established to analyze the energy superposition between each load stage and submarine structure vibrations. The submarine whipping response based on different energy constructions is simulated based on load disassembly. The simulation results are in good agreement with the sea trial data, indicating that the particle-spring system has significant advantages in a qualitative analysis of the submarine energy superposition owing to the torpedo near-field underwater explosives. The proposed method can be used as a theoretical reference for analyzing the damaging effect of a submarine structure whipping response of near-field underwater explosions caused by a torpedo.
torpedo; submarine; underwater explosion; whipping response; particle-spring system
郭志荣, 陆文俊, 金晓宇. 鱼雷爆炸作用下潜艇鞭状运动响应仿真分析[J]. 水下无人系统学报, 2021, 29(5): 609-615.
TJ630.1; TQ560
A
2096-3920(2021)05-0609-007
10.11993/j.issn.2096-3920.2021.05.014
2020-06-24;
2020-12-07.
郭志荣(1976-), 男, 博士, 副教授, 主要从事兵器工程研究.
(责任编辑: 杨力军)
