转子各参数对鱼雷涡轮机启动过程响应特性的影响
2021-11-08张盼盼史小锋
张盼盼, 宋 文, 史小锋, 伊 寅
转子各参数对鱼雷涡轮机启动过程响应特性的影响
张盼盼, 宋 文, 史小锋, 伊 寅
(中国船舶集团有限公司第705研究所, 陕西 西安, 710077)
为了研究转子各参数对启动过程响应特性的影响, 建立了鱼雷涡轮机转子系统简化单盘悬臂转子模型, 并利用Riccati传递矩阵法推导出该模型的瞬态运动微分方程, 引入Newmark-法对其进行求解, 完成启动过程响应分析, 重点讨论了角加速度、阻尼系数等参数对转子启动过程响应的影响规律, 得出角加速度增大, 共振幅值减小, 共振转速略有增大; 阻尼系数增大, 共振幅值减小, 共振转速略有减小。分析结果对转子瞬态动平衡的研究和弹性环的合理设计有一定的参考价值。
鱼雷; 涡轮机; 转子; 启动过程响应; Riccati传递矩阵法; Newmark-法
0 引言
为了满足鱼雷高航速、远航程的发展需求, 燃气涡轮机成为热动力鱼雷推进系统的发动机首选方案, 其功率潜力较大, 振动和噪音较小, 结构简单且便于加工。现代涡轮机的工作转速越来越高, 由于不平衡质量的存在, 转子在启动、加速、停机等响应过程中穿过临界转速区可能产生较大的振动[1], 因此应准确分析转子系统加速的响应特性, 并力求减小加速过程中通过临界转速时的最大响应幅值。研究表明, 减小转子系统的支承刚度来减小临界转速, 通过增大转子系统阻尼系数来减小共振幅值, 这些措施均可以降低转子系统穿过临界转速区域的振幅及外传力[2-3], 还可以提高启动角加速度, 使得转子在产生大幅值响应之前就能穿过共振区域, 这也是降低共振幅值的有效途径之一[4-5]。
轴系的瞬态响应计算在国内外已有很多研究, 主要以传递矩阵法或模态综合法为主, 并辅助以数值积分法。其中传递矩阵法由于建模灵活、计算效率较高, 无需建立转子系统的总体动力学方程, 被广泛应用于转子动力学领域上网线性链式系统的动力学问题。而直接积分法是在有限差分的思想基础上发展而来的微分方程组数值计算方法。直接积分法根据假定的位移、速度和加速度的不同变化形式, 有多种具体积分格式, 如常加速度法、Houbolt法、平均加速度法、线性加速度法、Newmark-法和Wilson-法[6]等。目前, 在求解自由度数很大的大型系统时, 多采用Newmark-法和Wilson-法及其改进形式。这些算法选取适当的参数后能够无条件稳定, 精度较高。如李涛等[7]利用传递矩阵法建立了偏置单盘转子的瞬态运动方程, 利用Newmark-法求解, 分析了单盘转子在稳态和起动加速过程中的突加不平衡响应, 总结了突加不平衡量的大小、转动加速度和系统阻尼对瞬态响应的影响。
文中针对鱼雷燃气涡轮机转子系统, 基于Riccati传递矩阵法建立单盘悬臂转子系统的瞬态运动方程, 引入Newmark-法对其求解, 仿真得到涡轮机转子系统在启动加速过程中的启动过程响应特性, 并总结了角加速度、阻尼系数等参数对启动过程响应的影响。
1 动力学仿真模型
1.1 涡轮机简化单盘悬臂模型
燃气涡轮机高速转子由涡轮盘、轴、花键套、输出齿轮轴和4个轴承等部分组成, 安装方式为外伸式。燃气涡轮机转子系统如图1所示[8]。
实际中转子系统是质量连续分布的弹性系统, 具有无穷多个自由度, 利用Riccati传递矩阵法对其简化后, 将轴段划分为均匀等截面轴, 将涡轮盘看作具有偏心质量的刚性圆盘。图2是采用Riccati传递矩阵法分析单盘悬臂转子启动过程响应的动力学简化模型。

图1 燃气涡轮机转子系统
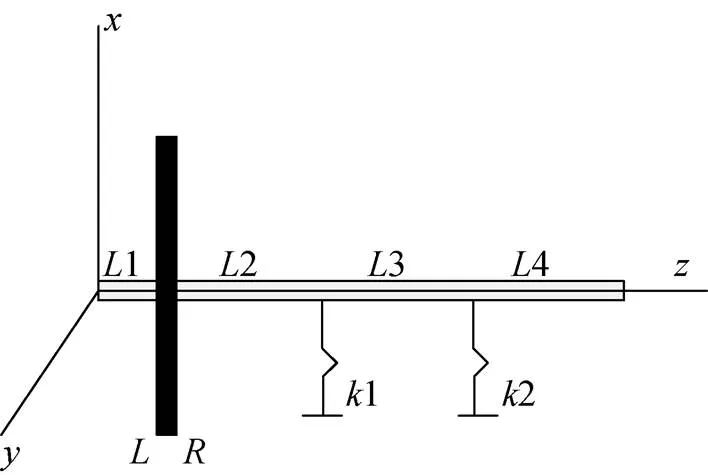
图2 燃气涡轮机简化单盘悬臂模型
可将涡轮盘看作外载荷, 涡轮盘左右端面挠度和弯角相同, 考虑到转子系统受到不平衡力以及加减速过程中的惯性力作用, 其附加弯矩以及剪力分别为

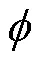
1.2 基于Riccati传递矩阵法的瞬态运动方程

弹性支承和轴段的传递矩阵分别为
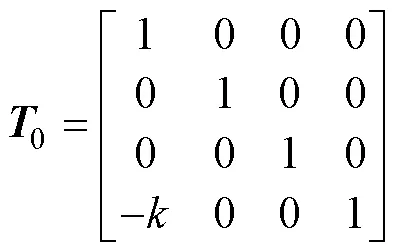
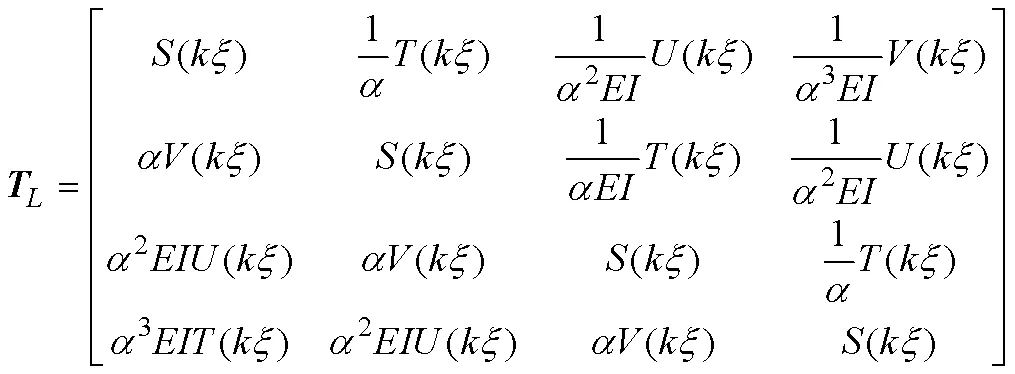
涡轮盘左侧截面的状态向量可以通过左端边界条件和轴段1的传递矩阵关系得到

式中:1是轴段1的传递矩阵, 通过上式变形得到

涡轮盘右侧截面的状态向量可以通过右端边界条件、支承和轴段的传递矩阵关系得到
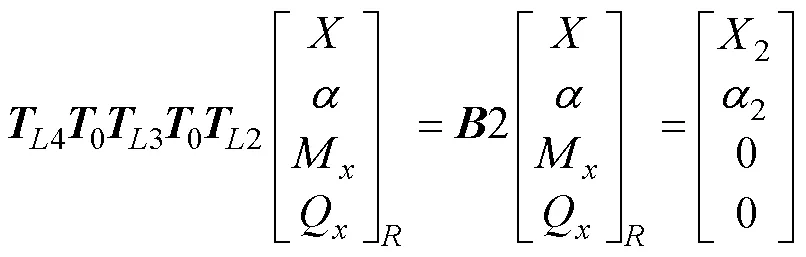
式中:2、3、4分别为段2、3、4的传递矩阵,0为弹性支承的传递矩阵。通过上式变形之后可以得到

由于涡轮盘左右两侧截面上的状态向量有
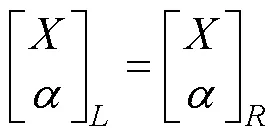
结合式(8), 式(5)和式(7)两式相减并整理之后可以得到
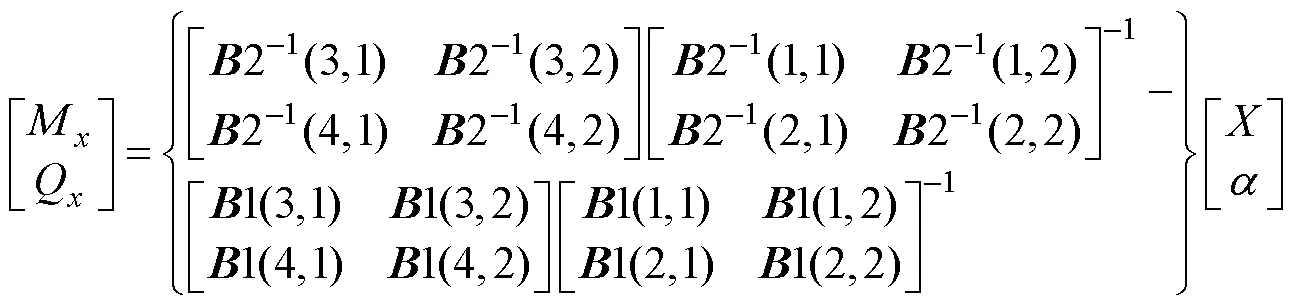
若

则式(9)可以变形为
由式(11)和式(1)可以得到转子系统的瞬态运动方程
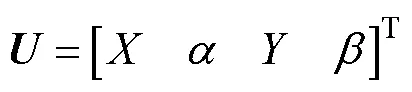
质量矩阵为
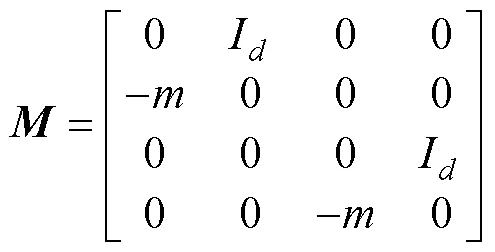
阻尼矩阵为

刚度矩阵为

外激励矩阵为
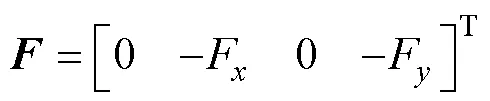
其中


1.3 Newmark-β法
Newmark法对线性加速度假定进行修正, 在+Δ时刻的速度和位移表达式中引入参数和, 建立由时刻的位移、速度和加速度到+Δ时刻的位移、速度和加速度的递推关系, 逐步求出各时刻的位移、速度和加速度。计算中采用如下近似表达式
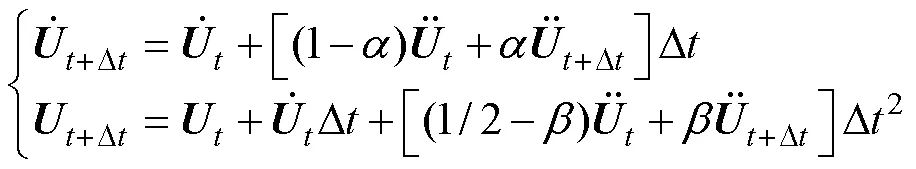
由式(19)可以得到
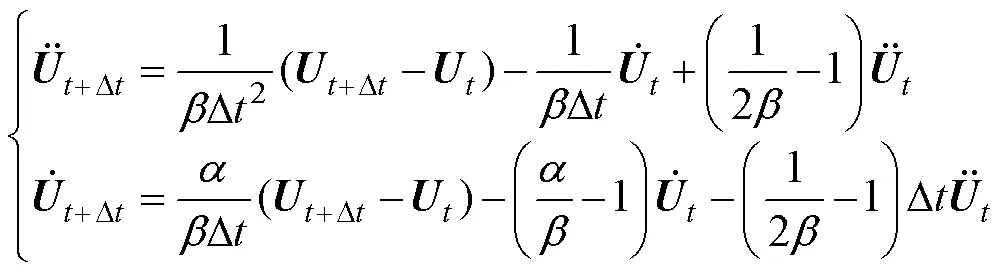
将式(20)代入+Δ时刻的动力方程, 得到
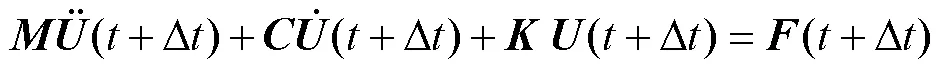
经整理后得到
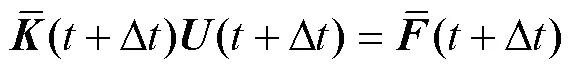
其中
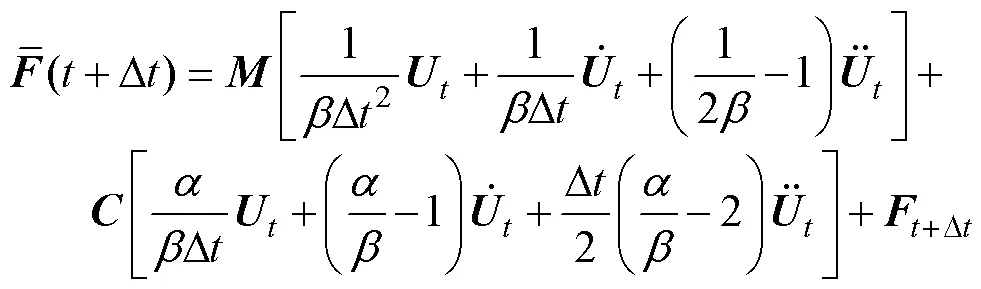
2 启动过程响应仿真分析

图3~图5分别为涡轮盘处和前后支承处的启动过程响应仿真结果。
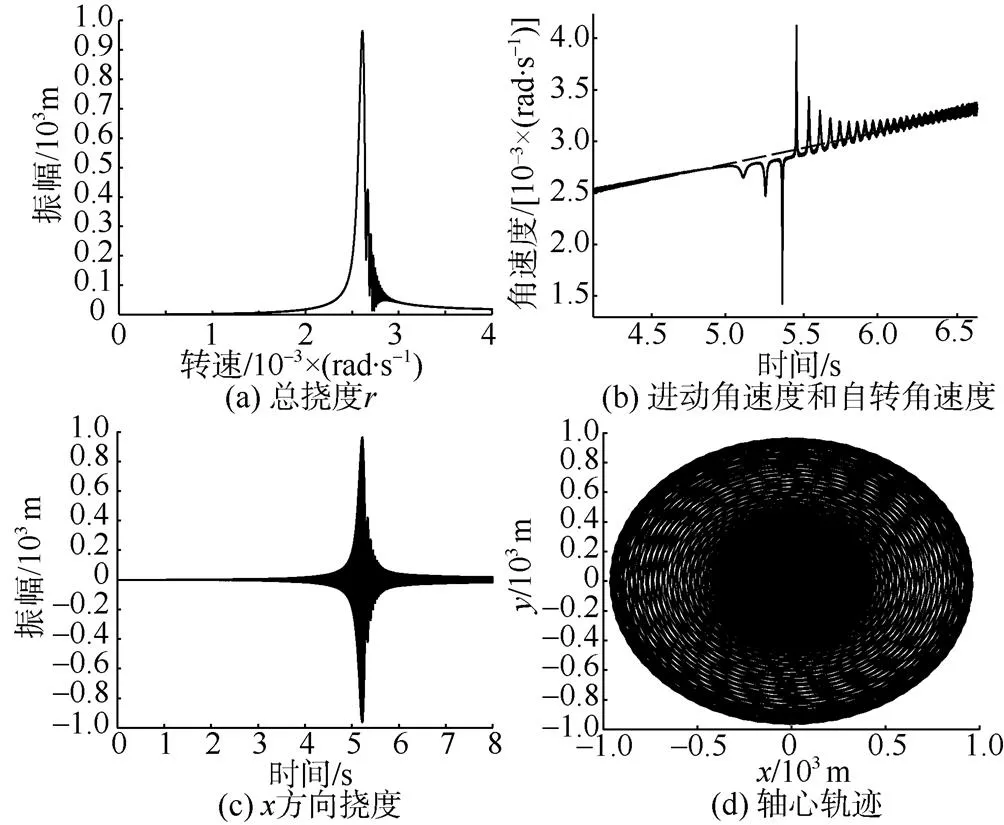
图3 涡轮盘处启动过程响应特性

图4 前支承处启动过程响应特性
图3~图5基本上可以反映出燃气涡轮机转子系统的加速度响应规律。以图3的启动过程响应进行分析。同时, 转子运行过程中涡轮盘、前支承和后支承处响应的最大共振幅值、共振时间以及共振转速见表1。

图5 后支承处启动过程响应特性

表1 不同角加速度下共振时间与振幅
由图3和表1可知:
1) 图3中(a)和(c)的启动过程响应趋势相同, 动挠度随着运行速度的增大而增大, 在临界转速附近出现峰值, 越过临界转速之后, 动挠度幅值快速下降, 并且以振荡波动的形式逐渐趋于稳定值。从表1可以看出, 由于涡轮盘具有较大的质量、惯性矩与转动惯量等, 所以涡轮盘处的共振幅值较大, 实际工况中应当特别关注涡轮盘处的振动。
2) 观察图3(b)可以发现, 刚开始转子系统运动不稳定, 进动角速度变化毫无规律且跳动幅度较大, 随着转子运行转速提高, 进动角速度和自转角速度趋于相等, 在图形中可以看到2个曲线基本重合, 当转子运行到临界转速附近时, 进动角速度开始围绕自转角速度出现波动, 波动幅值逐渐增大, 且在临界转速处达到最大值, 通过临界转速之后, 波动幅值开始减小, 随着时间的增加, 进动角速度又接近自转角速度, 在图形中2个曲线基本重合。
3 不同参数对启动过程响应的影响规律
3.1 角加速度对启动过程响应的影响

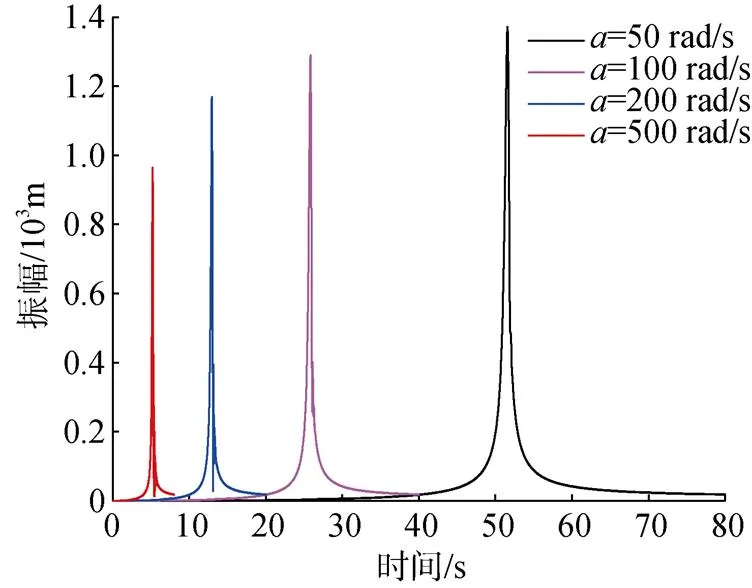
图6 不同角加速度下涡轮盘处总挠度曲线
从表2可以看出: 在转子运行过程中, 随着角加速度不断增大, 到达共振幅值需要的时间逐渐减小, 但两者变化幅度不是完全对应某种反比例关系。3个部件的最大响应幅值和共振转速随角加速度的变化趋势如图7和图8所示。

表2 不同角加速度下共振时间与振幅

图7 共振幅值随角加速度的变化

图8 共振转速随角加速度的变化
由图可知, 随着转子角加速度的增大, 转子系统3个部件启动过程响应的共振幅值逐渐减小, 角加速度较小时, 共振幅值的减小幅度较大, 当角加速度逐渐增大, 共振幅值减小的幅度逐渐变缓。因此, 可通过增大转子系统在运行过程中的角加速度, 来降低转子经过共振区域时的最大响应幅值。共振转速随着角加速度的增大而增大, 这主要是由于阻尼的滞后作用, 角加速度越大, 转子运转过程中经过临界转速所需要的时间越短, 振幅未及最大值就已经越过临界转速, 共振幅值将推迟出现[9]。当角加速度不断增大,共振转速增大的幅度在逐渐变小, 说明这种滞后效果随角加速度的增大而减弱。
实际上, 对燃气涡轮机转子系统来说, 不能为了降低共振幅值而过分地提高角加速度的大小, 随着角加速度的增大, 系统所需力矩及圆周方向的振动均会增大, 共振区推迟出现可能也会导致靠近工作转速发生剧烈振动, 文献[10]表明角加速度取在图7中曲线斜率最大处较为合适, 约为200 rad/s2。
3.2 阻尼系数对启动过程响应的影响
假设上述动力学计算模型的其他参数保持不变, 在转子启动过程响应过程中, 模拟转子的阻尼系数分别为0=10, 50, 100, 200, 300, 400 N·s/m, 通过仿真计算得到不同阻尼系数时涡轮盘、前支承和后支承处的总挠度随转速的变化规律。如图9所示(只给出部分阻尼系数的曲线), 表3给出了不同阻尼系数下完成启动过程响应所需总时间、到达共振区所需时间、涡轮盘、前支承和后支承处的共振幅值以及发生共振时的转子转速。
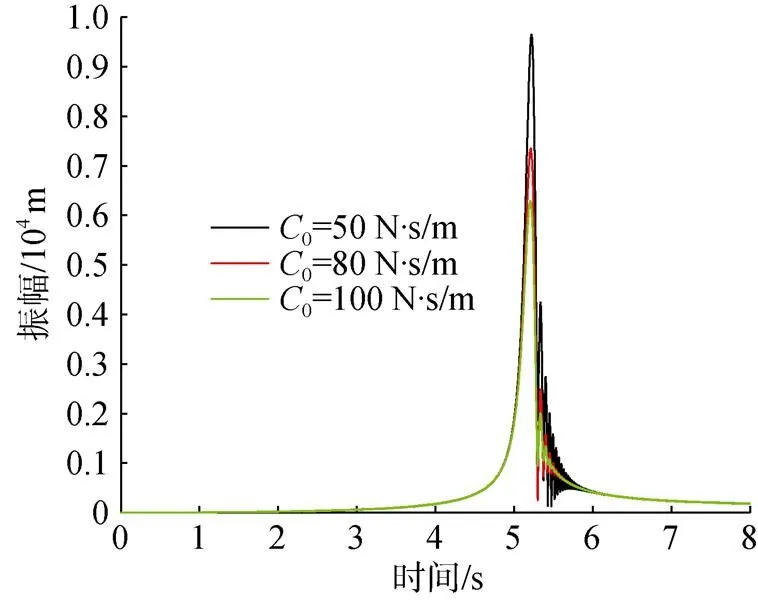
图9 不同阻尼系数下涡轮盘处总挠度曲线
3个部件的最大响应幅值及共振转速随阻尼系数的变化趋势如图10和图11所示。由图可知随着阻尼系数的增大, 启动过程响应的共振幅值逐渐减小, 这与实际情况相符; 阻尼系数较小时,共振幅值的减小幅度较大, 当阻尼系数越大时, 共振幅值减小的幅度变小, 共振幅值与阻尼系数是一种非线性关系, 阻尼系数对共振幅值的影响较大。转子系统发生共振时, 共振转速随着阻尼系数的增大而减小, 但变化幅度很大, 所以转子阻尼系数对临界转速的影响可以忽略。
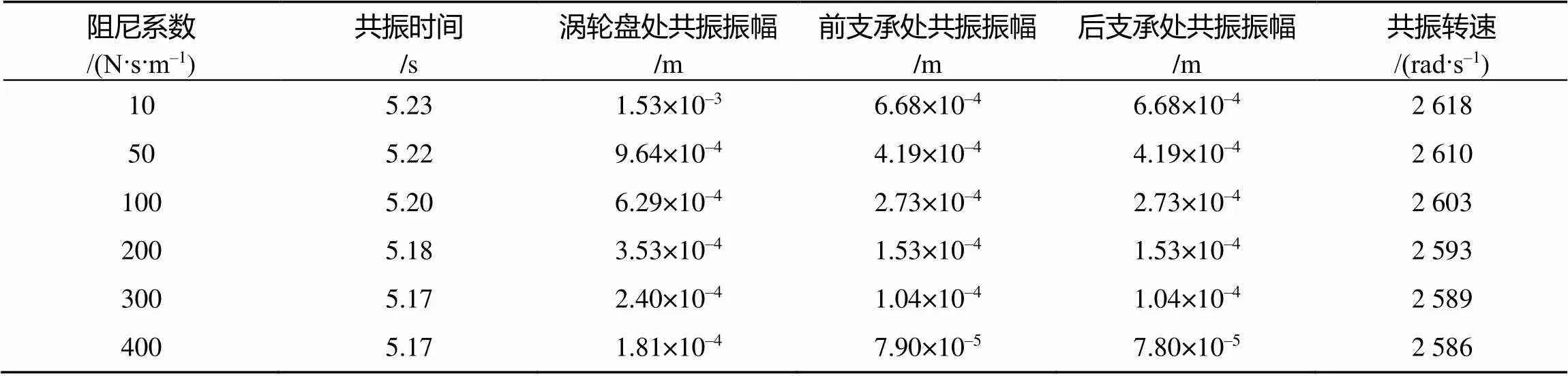
表3 不同阻尼系数下共振时间与振幅

图10 共振幅值随阻尼系数的变化
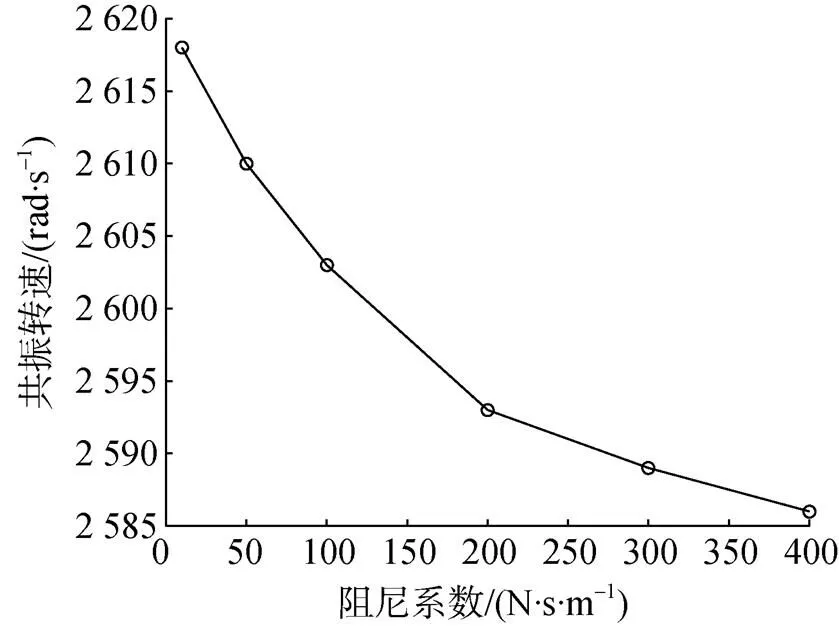
图11 共振转速随阻尼系数的变化
通过分析得知, 可通过增加转子系统阻尼, 来避免发生共振时幅值过大, 导致转子系统产生剧烈的振动, 损坏机械系统甚至造成更加严重的危害[11], 从图10中可以看出, 转子阻尼系数应选择在曲线的斜率变化最大处, 约为100 N·s/m。
3.3 同时改变角加速度和阻尼系数


表4 涡轮盘处的共振幅值随角加速度和阻尼系数的变化(单位: m)
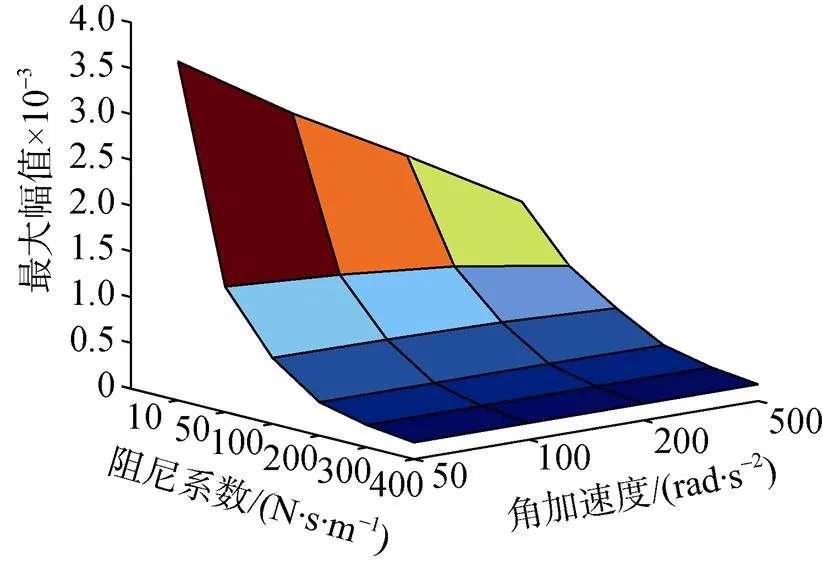
图12 共振幅值随角加速度和阻尼系数的变化
从表4和图12中可以看出: 阻尼系数对转子系统启动响应过程中共振幅值的影响比角加速度大, 故增加挤压转子系统油膜阻尼器, 尽可能增加转子阻尼来减小共振幅值是目前常用且有效的一种方法。涡轮盘与机匣之间的设计间隙为1×10–3m, 为了避免在转子系统运行过程中过临界转速时最大响应幅值大于转静子之间的间隙, 发生碰磨故障损坏机械结构, 必须考虑根据转子系统实际阻尼系数选择适当的角加速度, 当转子阻尼小于50 N·s/m时, 需要匹配更大的角加速度来满足设计要求; 当转子阻尼等于100 N·s/m时, 合适的角加速度值为200 rad/s2; 当转子阻尼大于200 N·s/m时, 合适的角加速度值为50 rad/s2。
4 结论
文中利用数值仿真方法研究了燃气涡轮机转子系统在启动过程中的启动过程响应, 分别分析了转子运行角加速度、转子阻尼系数以及支承刚度等对转子在经过临界转速区域时的共振幅值及共振转速的影响规律, 得到了以下几点结论。
1) 涡轮机转子系统在加速启动的过程中, 转子系统的运动状态相比稳态不平衡响应要复杂很多, 振动幅值随着各参数的变化出现明显波动情况, 瞬态响应所包含的信息比稳态响应丰富得多, 且更加接近转子实际中的运转情况。
2) 角加速度增大时, 转子系统共振幅值逐渐减小, 随着角加速度逐渐增大, 共振幅值减小的幅度慢慢变缓。共振转速也随角加速度增大而增大, 但增大的幅度不大, 越大的角加速度将会延迟启动过程响应出现发生共振的时间, 但不能为了降低启动过程响应共振幅值而过分增大角加速度, 角加速度值最好选择在振幅-角加速度曲线上斜率变化的最大处。
3) 阻尼系数增大, 启动过程响应的共振幅值逐渐减小, 阻尼系数较小时, 共振幅值的减小速率较大, 随着阻尼系数逐渐增大, 共振幅值减小的幅度变缓。阻尼系数对共振最大响应幅值的影响较大, 可以改变转子系统的阻尼系数来避免共振幅值过大, 导致转子产生剧烈的振动, 损坏机械结构。阻尼系数同样选择在振幅-阻尼系数曲线上斜率最大处为宜。文中同时给出了最大响应幅值随角加速度和阻尼系数变化的三维图, 可以为转子不同阻尼系数选择合适的运行角加速度, 避免转子系统发生碰磨故障。
[1] 钟一愕, 何衍宗, 王正, 等. 转子动力学[M]. 北京: 清华大学出版社, 1987.
[2] 李文忠. 高速转子系统振动控制技术评述[J]. 机械强度, 2005, 27(1): 44-49.
Li Wen-zhong. Review on Vibration Control Technology of High-speed Rotor System[J]. Journal of Mechanical Strength, 2005, 27(1): 44-49.
[3] 郑龙席, 李骁丰. 双盘转子系统各参数对转子瞬态响应影响的研究[J]. 机械科学与技术, 2010, 29(9): 1257- 1267.
Zheng Long-xi, Li Xiao-feng. Influence of the Double- rotor System Parameters on Its Transient Response[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(9): 1257-1267.
[4] 熊万里, 闻邦椿, 段志善. 转子系统瞬态过程的减幅特性及共振区迟滞特性[J]. 振动与冲击, 1999, 18(4): 12-15.
Xiong Wan-li, Wen Bang-chun, Duan Zhi-shan. Characteristics of Amplitude Decreasing and Resonance Band Delaying in Transient Processes of Rotor System[J]. Journal of Vibration and Shock, 1999, 18(4): 12-15.
[5] Millsaps T K, Reed L G. Reducing Lateral Vibrations of a Rotor Passing Through Critical Speeds by Acceleration Scheduling[J]. Journal of Engineering for Gas Turbines and Power, 1998, 120: 615-620.
[6] 贺威, 袁惠群. 多盘转子系统热启动过程中瞬态响应分析[J]. 机械制造, 2011, 49(3): 17-20.
He Wei, Yuan Hui-qun. Transient Response Analysis of Multi-disk Rotor System during Hot Start[J]. Mechanical Manufacturing, 2011, 49(3): 17-20.
[7] 李涛, 任兴民, 岳聪, 等. 单盘转子突加不平衡瞬态响应特征研究[J]. 机械科学与技术, 2012, 31(6): 924-927.
Li Tao, Ren Xing-min, Yue Cong, et al. Transient Response of Single-disc Rotor System under Sudden Unbalance Load[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(6): 924-927.
[8] 宋文, 梁跃, 伊进宝, 等. 三种升速条件下的鱼雷涡轮机转子系统动力学特性[J]. 动力学与控制学报, 2016, 14(3): 235-240.
Song Wen, Liang Yue, Yi Jin-bao, et al. Dynamic Properties of Torpedo Turbine Rotor System in Three Speed-up Processes[J]. Journal of Dynamic and Control, 2016, 14(3): 235-240.
[9] 张立, 罗兴起, 郭鹏程. 大型水轮发电机组轴系非线性瞬态响应分析[J]. 水力发电, 2006, 32(5): 48-51.
Zhang Li, Luo Xing-qi, Guo Peng-cheng. Dynamic Analysis of Non-linear Transient Response for Large Hydraulic Generator Unit[J]. Water Power, 2006, 32(5): 48-51.
[10] 丁鸿昌, 吕楠, 樊玉华. 转子系统穿越临界转速瞬态响应的振幅特性分析[J]. 制造业自动化, 2012, 31(6): 924-927.
Ding Hong-chang, Lü Nan, Fan Yu-hua. Analysis of Amplitude Characteristic for Rotor System Transient Response When Passing through Critical Speed[J]. Manufacturing Automation, 2012, 31(6): 924-927.
[11] 杨恩东, 孙虎儿, 苏飞. 有初弯的单盘转子等加速过临界时的瞬态响应分析[J]. 机械设计与制造, 2014(12): 30-32, 36.
Yang En-dong, Sun Hu-er, Su Fei. Transient Dynamic Responses of Unbalanced Jeffcott Rotor Speed Through the Critical with Initial Bending[J]. Machinery Design&Manufacture, 2014(12): 30-32, 36.
Influence of Rotor Parameters on Response Characteristics of a Torpedo Turbine during the Start-up Process
ZHANG Pan-pan, SONG Wen, SHI Xiao-feng, YI Yin
(The 705 Research Institute, China State Shipbuilding Corporation Limited, Xi’an 710077, China)
To analyze the influence of rotor parameters on the response characteristics of the startup process, a simplified single-disk cantilever rotor model of a torpedo turbine rotor system is established, and its transient differential equation is derived by using the Riccati transfer matrix method. Moreover, the Newmark-method is used to solve the startup process response of the rotor. The influence of the law of angular acceleration, damping coefficient, and other parameters on the response of the rotor during the startup process is analyzed. The results show that an increase in the angular acceleration leads to a decrease in the resonance amplitude and a slight increase in the resonance speed. Furthermore, an increase in the damping coefficient results in a decrease in the resonance amplitude and a slight decrease in the resonance speed. The results can be used as a reference and have theoretical significance for the research on transient dynamic balance and rational design of elastic ring structures of a rotor.
torpedo; turbine; rotor; start-up process response; Riccati transfer matrix method; Newmark-method
张盼盼, 宋文, 史小锋, 等. 转子各参数对鱼雷涡轮机启动过程响应特性的影响[J]. 水下无人系统学报, 2021, 29 (5): 601-608.
TJ630.32
A
2096-3920(2021)05-0601-09
10.11993/j.issn.2096-3920.2021.05.013
2020-09-08;
2020-12-08.
张盼盼(1995-), 女, 硕士, 主要研究方向为武器系统与运用工程.
(责任编辑: 许 妍)
