导弹倾斜发射不同时离轨初始扰动计算方法研究

杨 企，龙 军

(江南机电设计研究所，贵州 贵阳 550009)

0 引言

导弹离轨初始扰动是弹架系统设计的主要技术指标，也是导弹弹道设计、飞行控制方案设计的重要初始数据。对于采用倾斜发射不同时离轨发射方式的导弹而言，由于其离轨后会出现低头下沉现象，初始扰动较大，发射精度将受到严重影响[1]。目前，导弹发射扰动计算普遍采用建模仿真计算方法，该方法基于弹架系统物理模型，利用多体动力学仿真软件进行计算，可直观呈现导弹发射动态过程[2]。但是，由于仿真计算方法对物理模型的依赖性较强，在方案阶段必然存在以下两方面问题：一是没有弹架系统物理模型时，无法进行仿真计算，无法预估导弹发射扰动，不能指导发射箱/筒、发射导轨等关键部件的方案设计；二是弹架系统物理模型多次调整时，需要反复进行仿真计算，加之仿真工况较多，致使仿真工作量非常大，严重影响方案设计效率。

本文通过构建导弹发射动力学数学模型和仿真模型，分别利用理论计算方法和仿真计算方法对导弹离轨参数进行计算，并将理论值与仿真值进行对比分析，提出含标称值和散布值的导弹发射扰动数据，为方案阶段导弹弹道设计、飞行控制方案设计等提供依据。

1 发射动力学建模

1.1 数学模型

以发动机点火时刻为时间零点开始分析，导弹发射离轨运动过程分为闭锁阶段、导向阶段和滑离阶段。对三个阶段分别建立并求解导弹运动方程，可以计算不同高低射角和环境温度工况下导弹的离轨时间、离轨速度和离轨扰动。在分析过程中，把导弹视为刚体，建立运动方程，主要研究导弹俯仰平面质心的运动和绕质心的转动，不考虑偏航运动和滚转运动。导弹运动过程中，假设吊耳在导轨上无跳动(一般由导轨加工制造的波纹度保证)，且暂不考虑弹架系统弹性。

1.1.1 闭锁阶段

在闭锁阶段，导弹处于静止状态。导弹受到推力P、闭锁力T、重力G和前、后吊耳的支反力N1、N2，以及前、后吊耳与导轨间的摩擦力Ff1、Ff2，如图1所示。

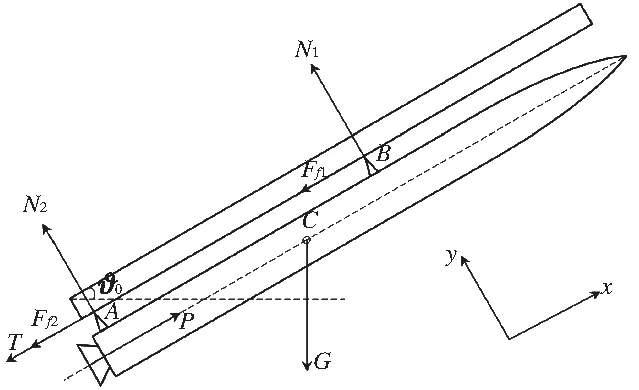
图1 闭锁阶段导弹受力示意图

闭锁阶段导弹静止数学模型如下：

P-T-mg(sinϑ0+μcosϑ0)=0

(1)

式中：m—导弹质量；g—重力加速度，可取g=9.8 m/s2；ϑ0—导弹高低射角；μ—摩擦系数，可取μ=0.15。

导弹起动条件如下：

P>T+mg(sinϑ0+μcosϑ0)

(2)

当发动机推力逐渐增大至满足式(2)后，在某一瞬间导弹开始运动。

1.1.2 导向阶段

在导向阶段，导弹平行于导轨滑移。导弹受到推力P、重力G和前、后吊耳的支反力N1、N2，以及前、后吊耳与导轨间的摩擦力Ff1、Nf2，气动力影响忽略不计，如图2所示。

图2 导向阶段导弹运动受力示意图

导向阶段导弹运动数学模型如下：

(3)

式中，vd为导弹质心速度。

1.1.3 滑离阶段

在滑离阶段，导弹前吊耳离轨，后吊耳仍在导轨上滑移，导弹在不平衡力矩作用下绕质心转动，产生下沉角φ。导弹受到推力P、重力G、后吊耳的支反力N以及后吊耳与导轨间的摩擦力Ff，气动力影响忽略不计，如图3所示。导弹俯仰角ϑ等于高低射角ϑ0与下沉角φ的差，弹道倾角θd等于高低射角ϑ0与下沉角φ和攻角α的差。

图3 滑离阶段导弹运动受力示意图

滑离阶段导弹运动数学模型如下：

(4)

式中：Jz—导弹对过质心C的z轴的转动惯量；LA—导弹后吊耳距导弹质心的距离(沿导弹轴向)；Rb—导弹质心距导轨滑行面的距离；ωz—导弹俯仰角速度。

对上述非线性动力学方程组(4)进行一系列分析、简化和推导，最终结果如下：

(5)

式中：Pa—导弹发动机平衡推力；t—导弹运动时间；t1—导弹前吊耳离轨时间；Δt—导弹不同时离轨时间；φ2—导弹离轨下沉角；ωz2—导弹离轨俯仰角速度。

根据导弹高低射角、推力、外形尺寸、质量、质心及转动惯量等数据，可计算得到不同射角和温度工况下导弹离轨时的速度、下沉角和俯仰角速度。

1.2 仿真模型

在ADAMS中建立只包含导弹和发射架的弹架系统刚体简化模型，设置导弹参数，施加约束与载荷，形成刚体发射动力学模型，如图4所示。

图4 刚体发射动力学模型

2 发射动力学计算

导弹高低射角范围为10°～72°，分别取10°、25°、40°、55°、72°射角，每个射角均计算低温(-40 ℃)、常温(20 ℃)、高温(50 ℃)3种工况，共计15种计算工况。

2.1 理论计算

基于发射动力学数学模型进行理论计算，导弹离轨参数计算结果如表1所示。

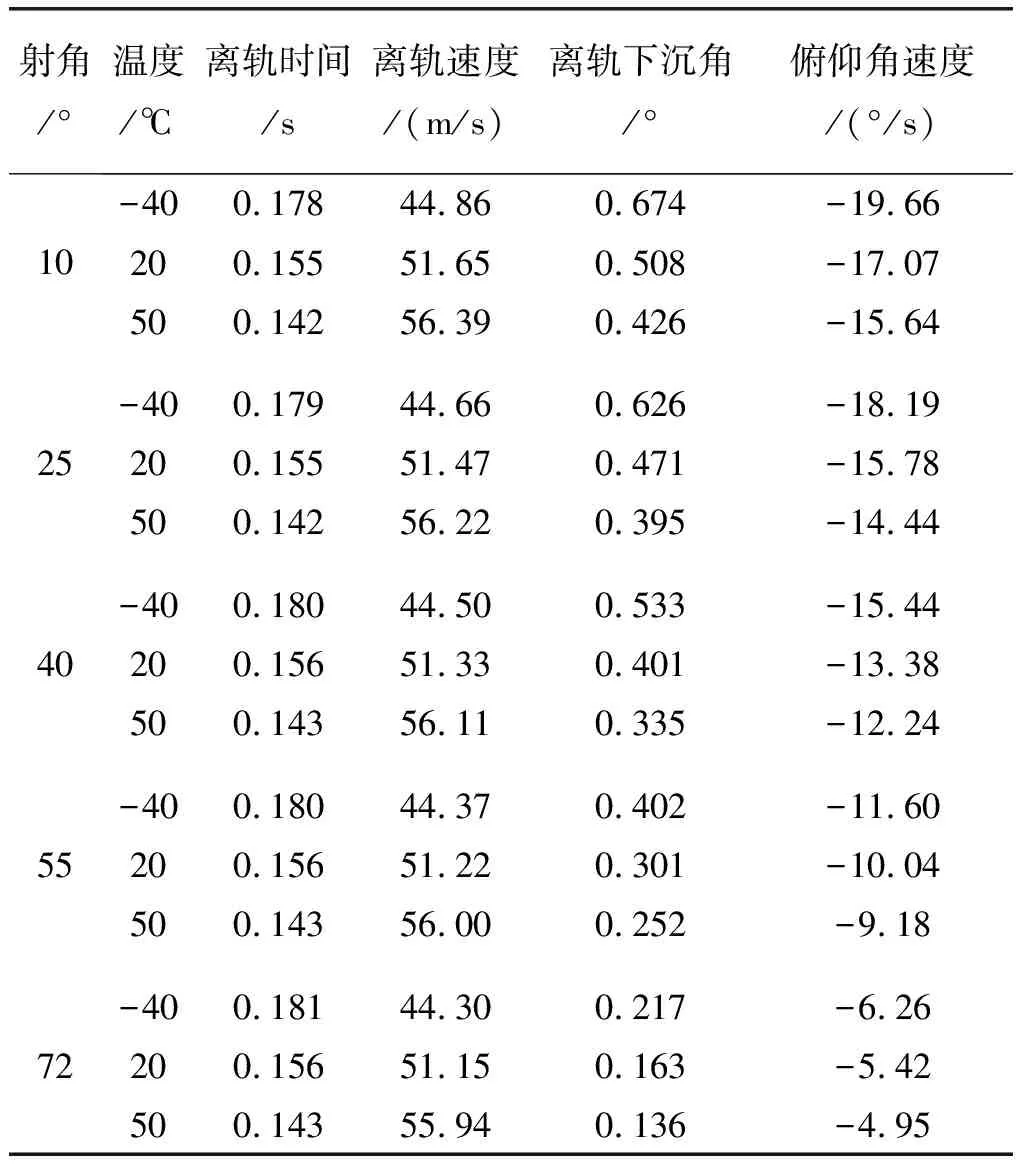
表1 导弹离轨参数理论计算结果

2.2 仿真计算

基于发射动力学仿真模型进行仿真计算，导弹发射过程仿真曲线如图5～图9所示，导弹离轨参数计算结果如表2所示。

表2 导弹离轨参数仿真计算结果

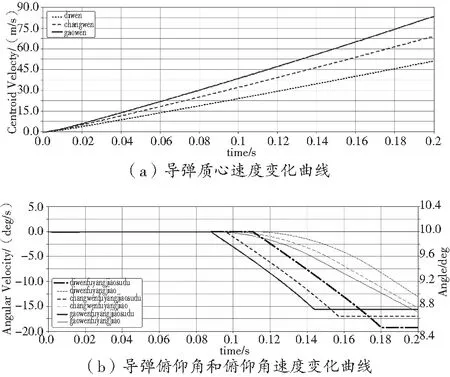
图5 10°射角导弹发射过程仿真曲线

图6 25°射角导弹发射过程仿真曲线

图7 40°射角导弹发射过程仿真曲线

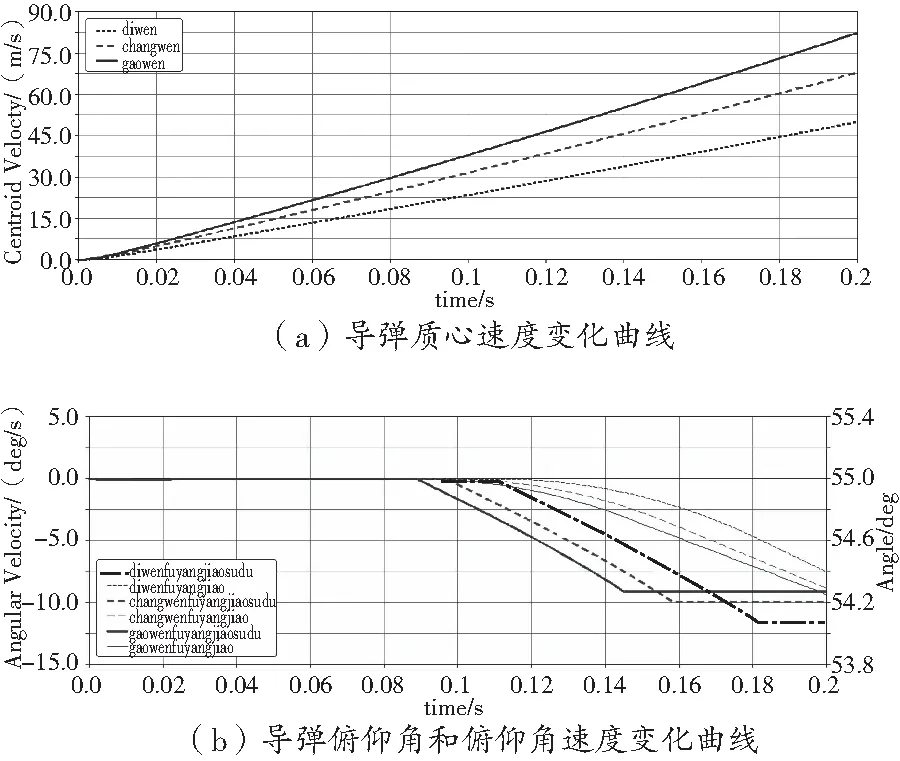
图8 55°射角导弹发射过程仿真曲线

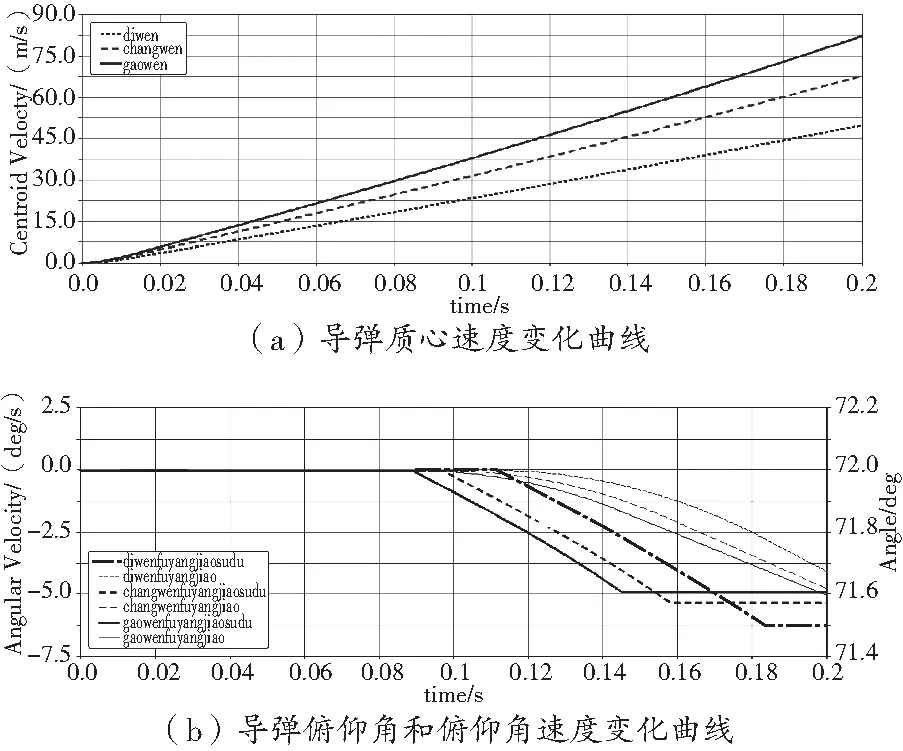
图9 72°射角导弹发射过程仿真曲线

3 结果分析

3.1 理论值与仿真值对比情况

将导弹离轨参数理论值与仿真值进行对比分析，对比情况如表3所示。

表3 导弹离轨参数理论值与仿真值对比情况

通过对比分析可以看出，导弹离轨参数理论计算结果与仿真计算结果非常吻合。

3.2 发射扰动数据(表4)

表4 导弹发射扰动数据(含散布)

根据上述理论计算结果与仿真计算结果，结合工程经验，提出含标称值和散布值的导弹发射扰动数据。

4 结论

本文针对导弹倾斜发射不同时离轨初始扰动问题，构建发射动力学数学模型和仿真模型，利用理论计算和仿真计算两种方法进行发射动力学计算，结果表明：导弹离轨参数理论计算结果与仿真计算结果非常吻合。鉴于导弹发射扰动仿真计算方法存在物理模型依赖性强、模型更改适应性差、仿真工作量大等突出问题，无法有效指导发射系统相关方案设计，而理论计算方法能够显著解决这些问题，因此武器系统方案阶段导弹发射扰动计算可直接采用理论计算方法。