基于滚轮式伸缩的被动激光跟踪测量系统搭建及其误差分析与补偿

张梦华，张记云，任伟鹏，耿万佳，娄志峰，范光照

(大连理工大学 机械工程学院，辽宁 大连 116000)

0 引言

在我国发展双循环的新发展格局下，工业机器人等高端制造装备国产化势在必行，在各行业使用密度也逐渐增加，因此对工业机器人的空间位置精度的测量装置的要求也不断提高[1]。激光跟踪仪作为一种突破测量空间局限的仪器，也逐渐广泛应用于工业机器人精度校正中。激光跟踪仪基于球坐标测量原理，由两角度测量模块组成，测量空间中两个角度与一个斜距表示被测点空间坐标。Cotne[2]利用基于网格测量方法从多方位测量一组固定目标位置建立了激光跟踪仪的运动学模型来校正激光跟踪仪误差。张亚娟[3]设计了单站式激光跟踪仪，对影响测量精度的机械结构误差进行了分析并提出标定的模型。ASME89.4.19[4]提出“双面测试方法”对跟踪仪进行精度校准，并阐述跟踪站两轴离轴量对测量结果的影响。激光跟踪仪采用主动跟踪的方式，具有复杂的跟踪控制系统，研制成本过高。范光照[5]提出了研制被动式激光跟踪球杆仪，本课题组设计了伸缩导轨取代了复杂的跟踪系统，由被测目标牵引伸缩导轨实现被动跟踪，基于多体系统误差理论建立了被动式激光跟踪球杆仪的误差模型，并提出单项误差标定方法[6-8]。但上述对被动式激光跟踪系统的研究中，装置伸缩部件采用层层垒叠的导轨组成，重量较大，且忽略光的偏移对系统测量精度的影响。

本文搭建了滚轮式被动激光跟踪测量系统，采用滚轮滑轨伸缩运动方式，对目标点实现被动跟踪测量，并对其主要误差源进行全面的分析，分步对各误差参数提出标定方法，最后通过比对验证补偿模型能有效提高系统空间定位精度。

1 滚轮式被动激光跟踪测量系统测量原理及误差补偿模型

1.1 滚轮式被动激光跟踪测量系统测量原理及坐标系的建立

本文提出的滚轮式被动激光跟踪测量系统，包括精密二维转台、滚轮滑轨伸缩机构、光栅测距装置以及滚轮滑轨直线度测量模块。精密二维转台两轴正交，滚轮滑轨伸缩机构通过转台两轴交点。如图1所示，此装置基于球坐标测量原理，采集精密二维转台俯仰轴、方位轴两角度编码器得到两角度位置信息，滚轮滑轨进行径向伸缩运动时采集贴于滚轮滑轨侧面的光栅尺(雷尼绍RGH24)得出长度位置信息，增加一束通过转台两轴交点的基准光(光轴)配合伸缩滑轨末端的光电位置传感器输出伸缩机构运动直线度误差。当测量目标点的位置时，滚轮滑轨末端的标准钢球吸附于被测物体上，当被测物运动时，带动标准钢球向俯仰、方位以及径向伸缩运动，标准钢球球心在三维球坐标系统中的坐标位置可表示目标点的位置。本文采用滚轮滑轨的伸缩运动方式，运动平滑，滑杆为碳纤维材料，重量小。采用光栅测距模块测量滚轮滑轨径向伸缩长度，简化了结构，成本较低，经济效益高。

基于多体系统误差理论对系统误差建模，首先需建立滚轮式被动激光跟踪测量系统的坐标系。滚轮式被动激光跟踪测量系统可由基座、方位轴、俯仰轴、滚轮滑轨伸缩机构四体连接组成，如图1所示建立坐标系，以方位轴为Z轴，方向背离地面向上，以方位角为0°时的俯仰轴的理论位置为X轴，通过右手定则确定Y轴，三轴交点即为原点。假设标准球球心在系统球坐标中位置为(φ,θ,R)，将其转换到笛卡尔直角坐标系中，则标准球球心在笛卡尔坐标系中的位置如式(1)：

图1 滚轮式被动激光跟踪测量系统测量原理图

(1)

1.2 滚轮式被动激光跟踪测量系统主要误差源分析

装置各零部件存在制造、装配误差，分析其主要误差源，如图2所示，主要存在方位轴与俯仰轴的离轴量Δy，不垂直度α；光轴与俯仰轴离轴量Δz、不垂直度β；光轴与方位轴离轴量Δx。另外由于滚轮滑轨变形使滑轨运动过程中存在X、Z两方向的直线度误差δx、δz。

图2 滚轮式被动激光跟踪测量系统轴系几何误差

1.3 滚轮式被动激光跟踪测量系统误差补偿模型

滚轮式被动激光跟踪测量系统工作过程可看成方位轴绕基座旋转φ，接着方位转台上部的俯仰轴旋转θ，最后与俯仰转台连接的伸缩滑轨径向移动R，即理想情况下，基座坐标系绕Z轴旋转φ，再绕X轴旋转θ，最后沿Y轴平移R到滚轮滑轨标准钢球坐标系中。其中R由伸缩滑轨结构基长R0与光栅尺Ra读数相加。由多体系统误差建模理论[9]可知，在此运动过程中滚轮滑轨末端即标准球球心坐标系到基座坐标系的理想转换矩阵如下：

(2)

当仅考虑上节所述静态几何误差时，误差矩阵如下：

(3)

设标准球球头中心在基座坐标系中实际坐标为P03=[XPYPZP1]，在球头坐标系中的坐标为TP=[0 0 0 1],则标准球球心在基座坐标系中实际坐标为：

P03=T01E01T12E12T23E23TP

(4)

由于误差值较小，将两个及两个以上误差项乘积忽略，则系统标准球球心在基座坐标系中实际坐标为：

(5)

2 误差模型参数的测量

2.1 Δy测量

测量方位轴与俯仰轴离轴量Δy时，在俯仰转台侧面放置一平面反射镜，万分表垂直接触镜面，在平面镜绕俯仰轴与方位轴旋转180°前后位置记录万分表示数变化，变化量即为方位轴与俯仰轴离轴量Δy的二倍。测量装置如图3所示，为减小平面镜安装姿态对测量结果的影响，测量前需调整平面镜使与通过方位轴以及旋转轴的平面平行，如图3(a)使用高精度光电自准直仪对准平面镜，调整平面镜姿态使绕方位轴以及俯仰轴旋转180°前后光电自准直仪读数不变，即可认为平面镜平行于方位轴以及俯仰轴。如图3(b),接着万分表垂直接触镜面，记录此时万分表读数，然后俯仰轴以及方位轴准确旋转180°(测角误差校正后)后记录万分表读数，两次读数差即为离轴量Δy的二倍。测量数据如表1所示，5次测量数据取平均得Δy=102.9 μm。

图3 Δy测量原理图

表1 Δy测量结果

2.2 α测量

如图4所示为方位轴与俯仰轴不垂直度α标定原理装置图，两面平面反射镜镜面垂直放置于俯仰轴两端。首先调整两面平面反射镜使镜面垂直与俯仰轴，利用高精度光电自准直仪照射镜面，调整平面反射镜姿态使其绕俯仰轴旋转一周内光电自准直仪读数不变，即可说明此平面反射镜与俯仰轴垂直，同理调整另一侧平面反射镜。然后保证调整后的平面反射镜姿态不变，使其绕方位轴准确旋转180度，记录旋转前后高精度光电自准直仪示数差，即为方位轴与俯仰轴不垂直度α的两倍。测量数据如表2所示，5次测量数据取平均得垂直度α为91.9″。

图4 α测量原理图

表2 α测量数据图

2.3 δx、δz的测量

滚轮滑轨径向伸缩运动时，由于滑轮与滑杆之间间隙以及滑杆自重的影响使伸缩机构运动过程中在二维平面内产生晃动，因此增加一束基准光(光轴)，光轴理论上通过俯仰轴与水平轴轴心，并通过牵引杆内照射到安装于伸缩滑轨末端的PSD上。当伸缩机构做径向伸缩运动时在二维平面内产生晃动时，以光轴为基准，两方向的偏差δx、δz可由PSD光电位置传感器读出，从而得出滚轮滑轨机构运动直线度并进行补偿。

2.4 R0、Δx及Δz的辨识

2.4.1 R0、Δx及Δz的辨识原理

滚轮滑轨结构初始长度即基长R0定义为：标准球球心到光轴出射点的最短距离。光栅测距装置测量的为相对位移，而滚轮滑轨伸缩机构绝对长度为俯仰轴与方位轴轴心到标准球球心的距离，即绝对长度等于初始长度R0与光栅尺读数的相对位移之和。

图5 R0、Δx及Δz的辨识原理图

如图5所示，高精度二维线性模组两轴正交，以辨识R0、Δz为例，由高精度二维线性模组带动装置仅沿竖直方向移动，设实际光轴与理想光轴存在偏差Δz即OF0，在高精度二维线性模组竖直运动方向上确定一初始位置，由于确定的初值位置伸缩滑轨伸出长度较短，可忽略伸缩滑轨变形，认为伸缩滑轨结构F0M0与光轴F0G0位于同一直线；当线性模组带动标准钢球沿竖直轴运动H时，伸缩滑轨绕O点转动θ，此时光轴运动至F1G1，由于伸缩滑轨伸长较长，存在变形，所以标准球头运动至M1，则M0M1=H，设初始位置与水平面存在夹角ε，则由几何位置关系解三角形OK0K1可得：

H={(R0+R1+Δztanε)2+

(6)

2.4.2 R0、Δz的标定实验

如图6所示，实验过程中，首先调整高精度二维线性模组竖直轴与水平轴垂直；其次调整转台基座底部旋钮使线性模组带动装置沿水平轴运动过程中二维转台俯仰角度示数不变，即可说明转台方位轴与线性模组竖直轴平行；接着在伸缩滑轨伸出长度最短处对光栅尺清零；然后运动至初始位置M0，记录二维转台俯仰角读数θ，已知光栅尺读数R1=0.037 mm；最后由线性模组带动标准钢球沿竖直轴从初始位置开始以间隔10 mm采集各点数据直至运动到线性模组竖直轴坐标150 mm处。记录竖直方向运动距离H、光栅尺读数R2、PSD示数z向变化量δz以及俯仰角度变化量θ。如表3，由多组离散数据根据式(6)进行最小二乘拟合得到：R0=1002.1510 mm，Δx=-0.7091 mm。

图6 测量实物图

表3 R0、Δz拟合数据表

2.4.3Δx的标定实验

光轴与方位轴离轴量Δx的辨识与Δz辨识同理，只需使线性模组带动标准钢球沿水平轴运动即可。几何关系表达式为：

(7)

线性模组带动标准钢球沿水平轴从初始位置开始以间隔10 mm采集各点数据直至运动到线性模组水平轴坐标150 mm处,记录水平方向运动距离H、光栅尺读数R2、PSD示数x向变化量δx以及方位角度变化量φ，已知R0=1002.151 mm，如表4所示由多组离散数据利用式(7)进行最小二乘拟合，得到：Δx=-0.7544 mm。

表4 Δx拟合数据表

2.5 β的辨识

2.5.1β的辨识原理

由于系统存在俯仰轴与方位轴之间的不垂直误差α、俯仰轴与光轴之间的不垂直误差β、滚轮滑轨直线度误差δx，使测量时方位角φ产生误差，如图7、图8所示，当线性模组带动标准钢球俯仰角度转过θ时，由于上述三项误差的存在，方位测角变化量为：

图7 α、β与Δφ的几何关系图

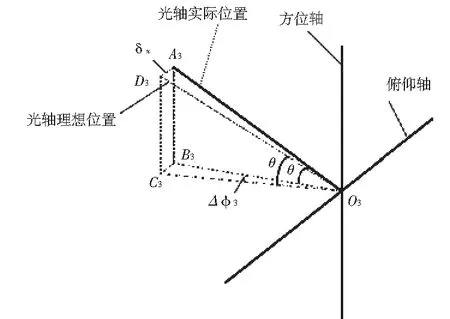
图8 δx与Δφ的几何关系图

Δφ=-arctan(sinαtanθ)+arcsin(sinβsecθ)+

(8)

2.5.2 β标定实验

与(2.4.2)R0、Δz的实验过程相同，线性模组竖直轴带动标准钢球从初始位置沿竖直方向以10 mm为间隔向上运动，每运动一次分别记录转台方位角变化量Δφ、俯仰角度变化量θ、PSD示数X向变化量δx、光栅尺示数Ra。已知R0=1002.1510 mm，α=91.9″，多组离散数据通过式(8)进行最小二乘拟合，拟合结果为：β=-21.6″。

表5 β拟合数据表

3 误差模型补偿比对验证

3.1 坐标转换

已知对于空间中两不同坐标系之间的复合转换，可以将其旋转与平移运动转换统一表示成4×4的齐次坐标转换矩阵。而由于不同设备具有不同的坐标系，对于空间内一点在不同的坐标系下具有不同的坐标。当一点在空间内运动时，不同的坐标系下也具有不同的轨迹方程，因此需统一坐标系。下边简要介绍空间内一点在两坐标系之间的坐标转换。当空间内一点在坐标系C中的坐标为(Xc，Yc，Zc),在坐标系D的坐标中(Xd，Yd，Zd),记坐标系D的原点在坐标系C中的坐标为L(3×1列向量)，由坐标系D的X、Y、Z三轴在坐标系C中的单位方向向量组成姿态矩阵R(3×3阶)，则有：

(9)

根据矩阵求逆运算规则，则：

(10)

3.2 比对实验

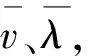
(11)

由于线性模组水平轴与竖直轴上测量点由跟踪测量系统三维坐标决定，因此验证滚轮式被动激光跟踪测量系统的空间定位精度时应同时考虑其X、Y、Z三方向的偏移量，即空间定位精度ΔL为：

(12)

由图9可知，测量线性模组X轴时，补偿前后滚轮式被动激光跟踪测量系统空间定位精度由585 μm提高到149 μm。由图10可知，测量线性模组Y轴时，补偿前后滚轮式被动激光跟踪测量系统空间定位精度由686 μm提高到152 μm。有效的补偿了滚轮式被动激光跟踪测量系统的误差。

图9 沿线性模组X轴运动空间定位精度

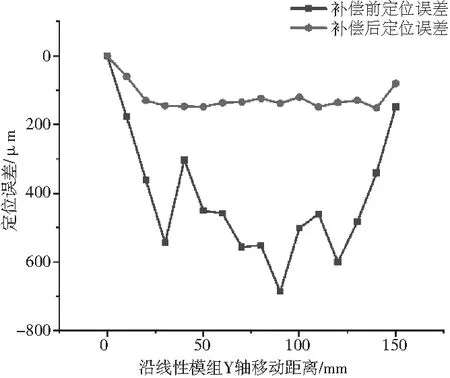
图10 沿线性模组Y轴运动空间定位精度

4 结束语

本文基于球坐标测量原理搭建了一台滚轮式被动激光跟踪测量系统，并对其进行了全面的几何误差分析，接着基于多体系统误差理论进行误差建模。然后对所有误差参数进行测量或辨识。最后与高精度二维线性模组进行单轴空间精度比对验证。本文有以下结论：

1)本文搭建的滚轮式被动激光跟踪测量系统，采用滚轮滑轨的形式实现伸缩运动；采用光栅测距的方式实现径向伸缩长度测量。全面分析系统主要误差源，并基于多体系统误差理论进行误差建模。

2)搭建了俯仰轴与方位轴的离轴量Δy、不垂直度α的标定装置，测得离轴量Δy=102.9 μm，α=91.9″。并利用高精度二维线性模组标定出R0=1002.1510 mm，光轴与俯仰轴的离轴量Δz=-0.7091 mm、不垂直度β=-21.6″，光轴与方位轴的离轴量Δx=-0.7544 mm。

3)将滚轮式被动激光跟踪测量系统与高精度线性模组坐标系统一后进行精度比对，结果表明沿线性模组竖直方向运动空间定位精度由585 μm提高到149 μm，水平方向空间定位精度由686 μm提高到152 μm。提高了其空间定位精度。