基于阻抗控制的机器人末端接触力控制系统研究

2021-11-07钱亚伟张雨航

现代机械 2021年5期

鲁航，钱亚伟，张雨航

(长安大学工程机械学院，陕西西安 710064)

0 引言

随着机器人技术的飞速发展，机器人的应用要求也不断提高[1]。机器人正面临许多复杂的工作环境，以位置控制为主的机器人难以适应如抛光、打磨、装配等复杂工作环境，如何在不同环境刚度下提高机器人与环境间的接触力稳定性和准确性已备受重视。由于液压驱动较小的活塞位移会产生较大的冲击力，与传统的末端执行器相比，加入弹簧作为柔性元件可以提高末端接触力的控制精度。

陈欢龙等人针对机械臂末端执行器与目标适配器导向插入过程中存在的碰撞问题，采用阻抗控制方法[2]，与传统位置控制相比，大大提高机械臂的接触力控制效果，但由于控制变量太多，在接触力太大的场合会产生很大的冲击。Uzunovic T等提出了一种同时控制位置和相互作用力的新算法[3]，位置和力控制合并为一个控制器，该控制器在位置和力控制之间的过渡是平稳的，但难以计算。Nagata将力/位置阻抗控制器应用于抛光机器人[4]，通过位置对抛光力进行调节，实现了沿CL数据的拾取进给控制和曲面上的稳定力控制，该方法难以适应环境的变化。

本文采用液压缸驱动，在活塞与环境之间设计了弹簧作为柔性元件，通过阻抗控制模型实现对接触力的控制，使其满足准确性的要求。

1 末端接触力系统建模

液压驱动的机器人与环境间接触力控制系统的组成及理论模型如图1。

图1 末端接触力系统理论模型

据流量连续性方程，伺服阀流量可表示为：

qL=Kqxv-KcpL

(1)

(2)

式中，qL=(q1+q2)/2是负载流量差，q1和q2是前进和后退的流量，m3/s；pL=p1-p2是负载压力差，p1和p2是前进和后退的压力，Pa；xv、xp、xL分别是阀芯、活塞和负载位移，m；Kq和Kc分别是阀的流量增益和流量压力系数；Ap是液压缸活塞腔有效面积；Ctp=Cip+Cep/2是活塞的总泄漏系数，Cip和Cep分别是活塞的内部泄漏系数和外部泄漏系数，m3/Pa；vt是两个腔室受压流体的总体积，m3；βe是液压油的有效体积弹性模量，MPa。

液压缸输出力与负载平衡方程：

(3)

式中，Mt是活塞和负载总质量，kg；Bp是活塞和负载的粘性阻尼系数，N·m/s；Ks是负载的弹簧刚度，N/m；FL是负载输出力，N。

对式(1)、式(2)、式(3)进行拉氏变换，可得：

QL=Kqxv-KcPL

(4)

(5)

AppL=Mts2Xp+BpsXp+KsXp+FL

(6)

由此可得液压缸活塞位移Xp，为：

(7)

可简化为：

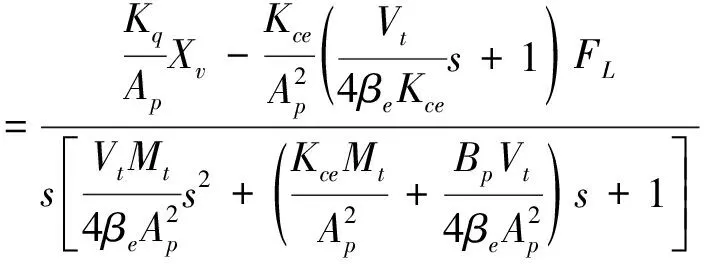
(8)

由式(8)得，活塞位移对阀芯位移Xv的传递函数：

(9)

对干扰外力FL的传递函数：

(10)

2 基于阻抗控制的末端接触力控制系统设计

2.1 弹簧的设计

在大冲击力下弹簧能够保护执行器不被损坏，弹簧刚度会直接影响机器人末端执行器控制性能，弹簧刚度越大，环境阻抗越大，不易进行柔顺控制调节，弹簧刚度越小，带宽越小，响应速度下降。因此，必须选择合适的弹簧刚度。

假设机器人所处工况的末端接触力为1000 N，根据《机械设计手册》[5]进行弹簧设计计算，根据所处工况，初步确定弹簧刚度为20000 N/m。

2.2 阻抗控制基本原理：

阻抗控制是将末端执行器与环境间的作用关系定义为质量-阻尼-刚度模型，使用阻抗模型可以描述末端执行器与环境之间的力/位动态关系，在控制过程中，通过调节阻抗模型中的参数，改变机械结构末端与接触环境的力/位关系，将力和位置控制纳入同一控制体系中[6]。阻抗控制基本原理如图2所示。

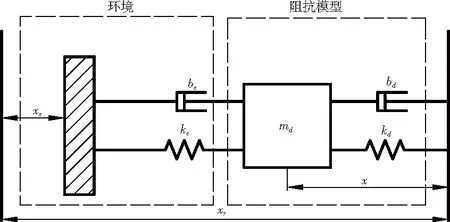
图2 阻抗控制基本原理图

阻抗模型常用的三种形式为：

(11)

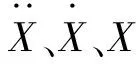
为了实现精确的力跟踪，引入一个期望力Fr，式(11)变为：

(12)

在阻抗控制中，常采用质量-阻尼-弹簧模型，令力偏差Fe=Fc-Fr，位置偏差Xf=X-Xr，则有：

(13)

由式(11)～式(13)得，阻抗模型为：

(14)

2.3 末端接触力控制系统设计

弹簧的压缩量为：

ΔX=Xp-XL

(15)

式中，ΔX是弹簧的压缩量；Xp是活塞位移；XL是负载位移。

(16)

式中，Fa是液压缸的输出力；ma是液压缸活塞质量；bs是液压缸的内部阻尼；Ks是弹簧刚度。

(17)

式中，mL是负载质量。

结合式(15)～式(17)，负载位移XL如下：

(18)

负载位移XL对液压缸位移Xp的传递函数：

(19)

对输出力FL的传递函数：

(20)

因此，基于阻抗控制的末端接触力控制系统示意图如图3所示,系统模型参数如表1所示。

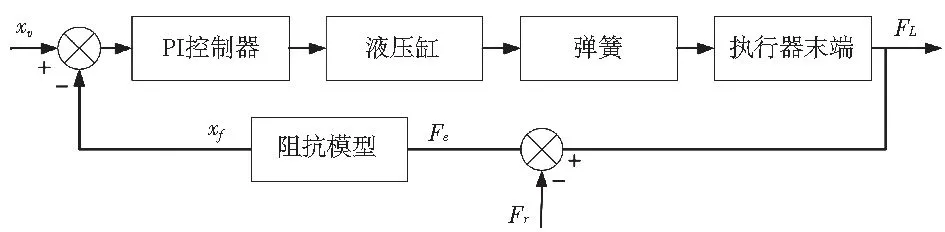
图3 基于阻抗控制的末端接触力控制系统示意图

表1 末端接触力模型的参数值

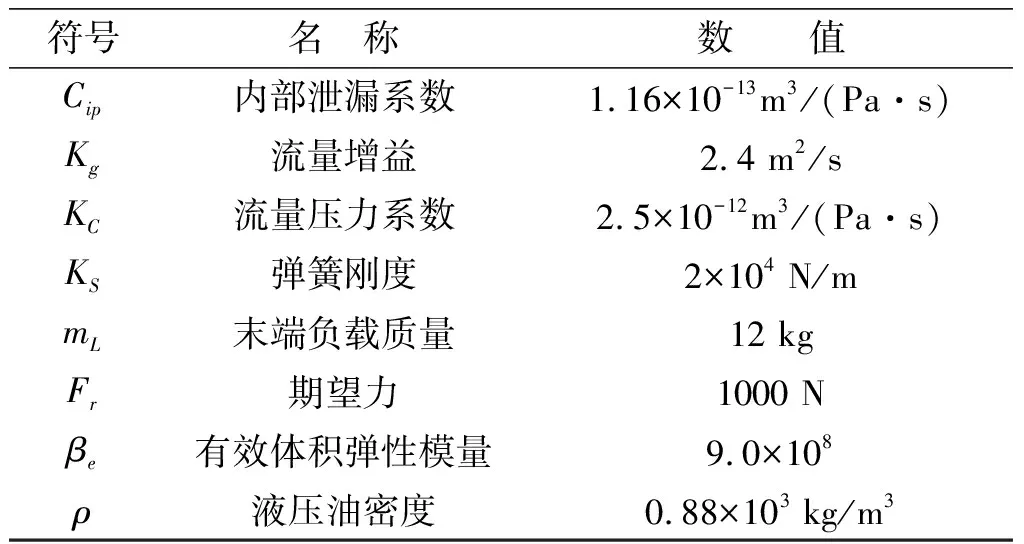
续表1

3 性能分析与仿真

假设机器人末端直接与环境接触产生作用力，期望接触力Fr=1000 N，稳态误差不超过5%，使用PI控制器在不同弹簧刚度和不同环境刚度下分别对其进行闭环反馈控制。根据图3的控制结构及表1中的参数，在SIMULINK中搭建仿真模型，如图4所示。

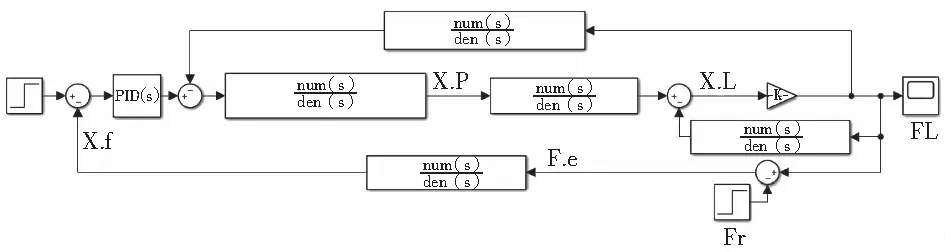
图4 末端接触力控制系统仿真模型

3.1 不同弹簧刚度

根据假设的接触条件，其中，根据拟定弹簧刚度Ks=2×104N/m取三种，分别为1×104N/m、2×104N/m、4×104N/m，环境刚度KL=2×104N/m。基于PI控制器，取Kp=0.001，Ki=0.00001。如图5所示，随着弹簧刚度Ks的增大，系统响应速度加快，过渡过程波动增大，达到稳态的时间缩短，系统稳定后的接触力略微减少。仿真结果表明，当Ks分别为1×104N/m、2×104N/m、4×104N/m时，系统稳态误差分别为2.85%、2.43%、2.21%，符合期望接触力准确性的要求。