砂带磨削接触压强模型分析与实验*
2021-11-06王亚杰
王亚杰, 黄 云
(1.郑州航空工业管理学院 航空工程学院, 郑州 450046)(2.重庆大学 机械与运载工程学院, 重庆 400044)
砂带磨削去除材料是个十分复杂的过程,磨削压力是影响材料去除效率的重要因素。在航空发动机叶片的砂带磨削加工中,把控制磨削压力作为精准去除材料的主要手段。但是,橡胶接触轮由金属材质的轮毂和高弹性材料的橡胶圈组成,橡胶接触轮与叶片之间的接触压强分布不均,从而使接触区域的材料去除效率不均匀。
为了获取接触区域压强分布的规律,ZHANG等[1-2]将接触轮与工件之间的接触近似为 Signorini 接触模型,利用该模型进行了有限元仿真分析,并建立了基于支持向量机(support vector machine,SVM)智能算法的接触压强计算模型;又采用基于神经网络的磨削接触力模型,对压力进行分析和预测。为了得到曲面工件磨削的接触压强分布,张雷等[3-4]将圆柱形接触轮与工件接触视为赫兹接触,开展了其表面去除模型的研究,尽管各向同性弹性体之间的接触符合赫兹定律三准则,但并未考虑接触轮的轮毂对接触压强分布的影响。王亚杰[5]开展了压力、接触轮对接触压强分布影响规律的研究与实验,却未总结出压力、接触轮等因素对接触宽度和最大接触压强的影响规律。SUN等[6-7]将赫兹接触理论引入到表面开槽接触轮与工件的接触中,其有限元仿真分析以及实验测量结果表明赫兹理论计算的理论值误差较大,不适用于开槽接触轮接触时的情况。刘斐等[8]针对弹性力学平面问题,采用复变函数解法求解了接触区域的压强分布规律。
上述文献尚未充分验证赫兹接触在砂带磨削中应用的准确性。本研究针对圆柱接触轮,进行砂带磨削接触压强分析,研究接触轮厚度比、橡胶硬度和接触压力对接触压强的影响,并开展平面试件和圆柱试件磨削验证实验。
1 砂带磨削接触模型
1.1 赫兹接触模型
赫兹提出,两曲面物体在适当作用力下接触并压紧,材料在初始接触点的附近发生局部变形,接触区域为椭圆形,接触压强按半椭圆球分布[9-10],如图1、图2所示。
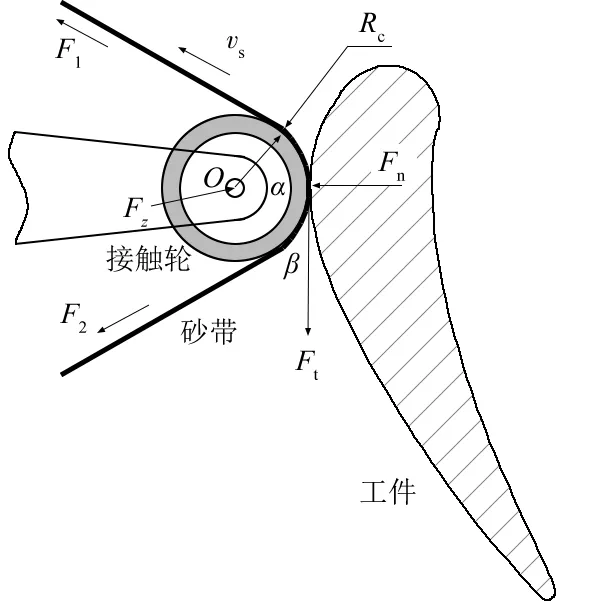
图1 接触轮与工件接触受力示意图
赫兹接触理论满足如下基本假设[9]:(1)接触区域发生小变形;(2)接触面呈椭圆形;(3)相接触的物体可被视为是弹性半空间,接触面上只作用有分布的垂直力。
在叶片砂带磨削加工过程中,橡胶接触轮与叶片的接触压力很小(低于10 N)。根据橡胶的应力-应变曲线,接触轮的橡胶处于较小应力下,应力和应变近似为线性关系。实验发现,二者接触面为椭圆形。
由图1可知:接触轮绕着轴O旋转,尽管砂带与叶片之间有摩擦力Ft,但是,接触轮并不承受这一摩擦力,而只承受磨削压力Fn。
F1·sinα=Ft+F2·sinβ
(1)
式中:α和β分别为F1、F2与Ft的夹角。
在数值上有:
Ft=F1-F2
(2)
因此,叶片砂带磨削状态近似满足赫兹接触理论的基本假设。图2中,a和b为椭圆形接触区域的长半轴和短半轴,p0为最大接触压强。

图2 半椭圆球面压强分布
当施加压力为Fn时,接触最大压强p0可以表示为:
(3)
接触区域的接触压强分布p(x,y)呈半椭圆球形状分布。
(4)
(5)
1.2 有限元接触模型
橡胶是一种大变形和高弹性的超弹性材料[8-10],在外力作用下发生较大形变,外力撤销后可以恢复到原来的形状。在接触轮的轮毂上包裹一定厚度的橡胶,磨削过程中可起到良好减震效果。
采用Mooney-Rivlin模型分析和计算橡胶材料的力学性能。当应变不超过150%时,Mooney-Rivlin模型[11-13]中应变能函数W可近似表述为:
W=C10(I1-3)+C01(I2-3)
(6)
式中:I1和I2分别为第一和第二Green应变不变量,参数C10和C01均为材料实验数据的回归系数。橡胶材料参数[9]如表1所示。

表1 橡胶材料仿真参数
为了便于实验和测量,选用平面和圆柱工件进行分析。接触区域和接触压强呈对称分布,只需建立接触轮的1/2有限元模型。相对于橡胶的变形量,轮毂和工件的变形可以忽略不计,将其简化为刚体。细化接触区域的网格,尺寸大约为0.05 mm,如图3所示。
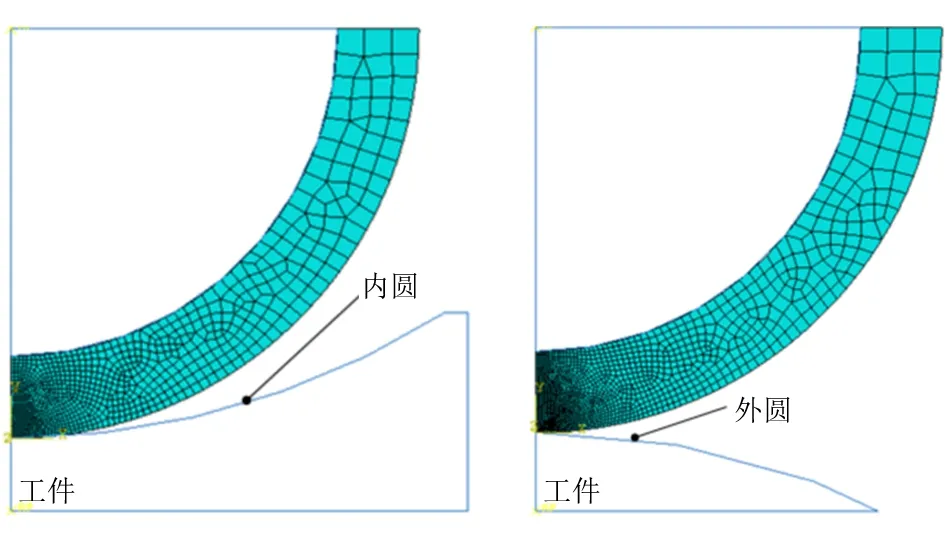
图3 砂带磨削有限元接触模型
2 结果与分析
橡胶接触轮与工件接触的应力云图如图4所示。为了分析厚度比、橡胶硬度和接触压力等参数对接触压强分布规律的影响,在分析结果中获取接触区域的节点应力,绘制接触区域的应力变化曲线。
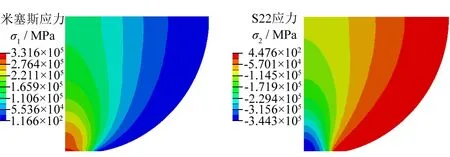
图4 橡胶接触轮有限元模型应力云图
厚度比为橡胶厚度与接触轮半径的比值。图5所示为不同厚度比对接触压强分布规律的影响。由图5可知:对于不同的厚度比rt,沿着x轴方向,有限元分析获得接触区域的压强均呈半椭圆形分布;厚度比越小,最大接触压强越大,而接触宽度越小;当厚度比rt为20%时,有限元分析得到的压强分布与赫兹接触模型的理论值最接近。
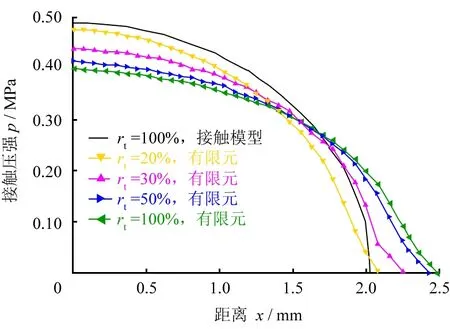
图5 厚度比对接触压强分布规律的影响
图6为不同橡胶硬度对接触参数的影响:橡胶肖氏硬度越大,最大接触压强越大而接触宽度越小;当橡胶肖氏硬度H小于60 HS时,随着橡胶硬度的增加,接触宽度急剧减小;当橡胶肖氏硬度H大于60 HS时,随着橡胶硬度的增加,接触宽度变化较为平缓。
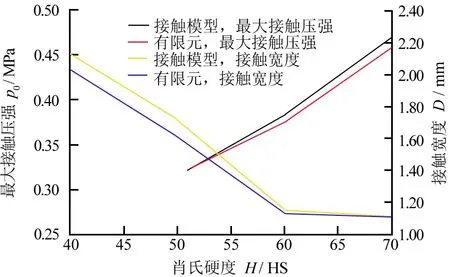
图6 不同橡胶硬度对接触参数的影响
图7所示为不同接触压力对法向接触参数分布的影响。由图7可以看出:由于橡胶的非线性,随着接触压力Fn的增大,最大接触压强和接触宽度逐渐增大,而有限元模型与赫兹接触模型分析得到的最大接触压强和接触宽度数据之间的差距逐渐增大;当接触压力达到50 N时,最大接触压强差达到了0.16 MPa,接触宽度相差0.87 mm。
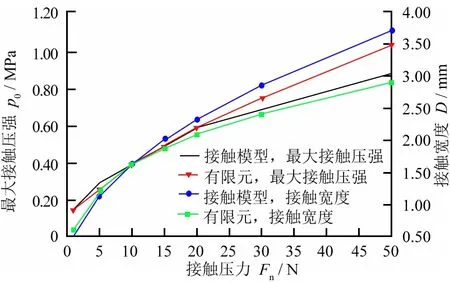
图7 接触压力对接触参数的影响
叶片表面由凹、凸曲面组成,叶片表面的曲率影响接触压强的分布,如图8所示。对于凹曲面(曲率半径为负数),曲率半径越小,有限元模型数据与赫兹接触理论结果之间的差距越小;对于凸曲面(曲率半径为正数),在相同的接触压力下,最大接触压强差别较大,这是因为凸曲面与圆柱接触轮的接触面积更小。

图8 不同工件曲率半径对接触参数的影响
3 接触实验
3.1 与平面工件的接触测试
为便于测试磨削过程中工件表面的接触宽度,设定工件宽度小于接触轮的厚度,放置位置如图9所示。施加的压力在工程许可范围内,采用不同的肖氏硬度H和接触轮半径R,磨削后测量的接触宽度如图10所示。

图9 磨削平面试件示意图

图10 接触测试的平面试件
图11显示了接触宽度随着接触压力呈非线性增大的变化规律,其测量值与有限元分析和赫兹接触模型理论值均十分接近。
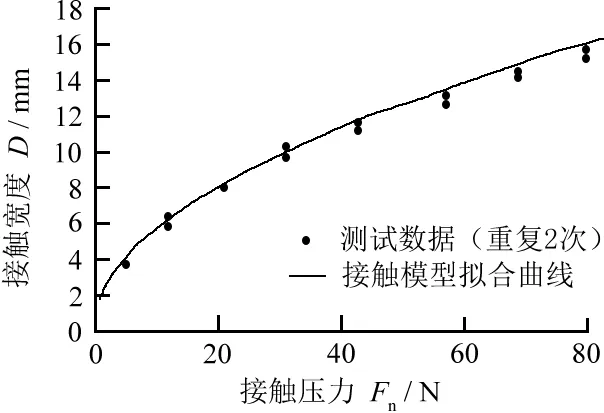
(a)H=65 HS,R=140 mm
3.2 与圆柱工件的接触测试
赫兹接触理论表明:当2个圆柱物体接触且轴线平行时,接触区域为矩形;当2个圆柱物体接触但轴线不平行时,接触区域为矩形或椭圆形。为了便于实验和测量,将圆柱试件的轴线摆放在与接触轮轴线垂直的位置,如图12所示。

图12 磨削圆柱试件示意图
实验用接触轮半径为140 mm,橡胶的肖氏硬度为45 HS,圆柱试件半径为10 mm。图13所示为接触后的圆柱试件表面。由图13可见:接触区域为椭圆形,椭圆形的长半轴与圆柱试件的轴线同向。这是因为接触轮的半径大于圆柱试件的半径。

图13 接触后的圆柱试件表面
图14所示为接触区域椭圆接触斑尺寸随接触压力的变化。从图14可以看出:随着接触压力的增大,长、短半轴的长度均呈非线性增大;长、短半轴的测试数据均与赫兹接触理论值保持一致;随着接触压力的增大,相比于长半轴,短半轴增量平缓。这是因为圆柱试件的半径远小于接触轮的半径,除了接触压力外,其他实验条件未改变,长、短半轴的比值也是恒定的。
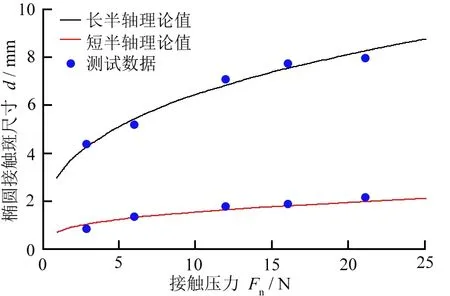
图14 椭圆接触斑尺寸随接触压力的变化
4 结论
从赫兹接触的基本假设角度,分析砂带模型接触状态;通过有限元分析和实验验证砂带磨削接触采用赫兹接触理论的准确性,得出如下结论:
(1)用于磨削的切向力Ft被张紧力抵消,并未作用在接触轮上。忽略影响较小的因素,砂带磨削接触状态基本符合赫兹接触理论。
(2)通过ABAQUS有限元软件,建立接触轮与工件接触的有限元模型,分析橡胶硬度、厚度比、接触压力以及工件曲率半径等因素对最大接触压强和接触参数的影响。当厚度比为20%和橡胶肖氏硬度为70 HS时,橡胶接触轮的接触压强分布与赫兹接触理论之间的误差最小。当接触压力低于15 N时,有限元模型与赫兹接触理论数据曲线几乎重合,满足工程应用要求。相对于凸曲面,接触轮与凹曲面工件接触误差较小。
(3)通过平面和圆柱工件与圆柱接触轮接触的测试实验,验证了建立的有限元模型和接触模型的准确性,说明赫兹接触理论适用于砂带磨削。
